Building Java Programs Chapter 13 Searching and Sorting

Chapter outline n Searching and sorting in the Java class libraries n n n Program efficiency n n n sequential and binary search sorting shuffling custom ordering with Comparators algorithm analysis complexity classes and Big-Oh notation Implementing searching and sorting algorithms n n n binary search selection sort merge sort Copyright 2006 by Pearson Education 2

Searching and sorting in the Java class libraries reading: 13. 1 Copyright 2006 by

Sequential search n Imagine searching for a particular word in an Array. List of words from a book: int index = words. index. Of(word); if (index >= 0) { System. out. println(word + " is word #" + index); } else { System. out. println(word + " is not found. "); } n sequential search: One that examines each element of a list in sequence until it finds the target value or reaches the end of the list. n The index. Of method above uses a sequential search. index 0 1 2 3 4 5 6. . . value It was the best of times it. . . Copyright 2006 by Pearson Education 4

Binary search algorithm n binary search: An algorithm that searches for a value in a sorted list by repeatedly eliminating half the list from consideration. n n n Can be written iteratively or recursively implemented in Java as method Arrays. binary. Search in java. util package Algorithm pseudocode (searching for a value K): n n Start out with the search area being from indexes 0 to length-1. Examine the element in the middle of the search area. n n If it is K, stop. Otherwise, n n n If it is smaller than K, eliminate the upper half of the search area. If it is larger than K, eliminate the lower half of the search area. Repeat the above examination. Copyright 2006 by Pearson Education 5

Binary search example Copyright 2006 by Pearson Education 6

Using binary. Search n Java provides two binary search methods: n Arrays. binary. Search (for an array) // binary search on an array: int[] numbers = {-3, 2, 8, 12, 17, 29, 44, 58, 79}; int index = Arrays. binary. Search(numbers, 29); System. out. println("29 is found at index " + index); n Collections. binary. Search (for a List) // binary search on Array. List with the same values: int index = Collections. binary. Search(list, 29); System. out. println("29 is found at index " + index); n n Note that the values in the array / list are in sorted order. If they are not, binary. Search is not guaranteed to work properly. Copyright 2006 by Pearson Education 7

Sorting n sorting: Rearranging the values in a list into a given order (often into their natural ascending order). n n One of the fundamental problems in computer science Many sorts are comparison-based (must determine order through comparison operations on the input data) <, >, compare. To, … index 0 1 2 3 4 5 6 7 value 15 2 8 1 17 10 12 5 index 0 1 2 3 4 5 6 7 value 1 2 5 8 10 12 15 17 Copyright 2006 by Pearson Education 8

Sorting in the class libraries n Java provides two sorting methods: n Arrays. sort (for an array) // demonstrate the Arrays. sort method String[] strings = {"c", "b", "g", "h", "d", "f", "e", "a"}; System. out. println(Arrays. to. String(strings)); Arrays. sort(strings); System. out. println(Arrays. to. String(strings)); n Output: [c, b, g, h, d, f, e, a] [a, b, c, d, e, f, g, h] n Collections. sort (for a List) Copyright 2006 by Pearson Education 9

Shuffling n shuffling: Rearranging the elements of a list into a random order. n Java has a shuffle method for a List, Collections. shuffle: String[] ranks = {"2", "3", "4", "5", "6", "7", "8", "9", "10", "Jack", "Queen", "King", "Ace"}; String[] suits = {"Clubs", "Diamonds", "Hearts", "Spades"}; Array. List<String> deck = new Array. List<String>(); for (String rank : ranks) { // build sorted deck for (String suit : suits) { deck. add(rank + " of " + suit); } } Collections. shuffle(deck); System. out. println("Top card = " + deck. get(0)); n Output (for one example run): Top card = 10 of Spades Copyright 2006 by Pearson Education 10

Custom ordering with Comparators reading: 13. 1 Copyright 2006 by Pearson Education 11

Custom ordering n Sometimes, the default ordering is not what you want. n Example: The following code sorts the strings in a case-sensitive order, so the uppercase letters come first. We may have wanted a case-insensitive ordering instead. String[] strings = {"Foxtrot", "alpha", "echo", "golf", "bravo", "hotel", "Charlie", "DELTA"}; Arrays. sort(strings); System. out. println(Arrays. to. String(strings)); n n Output: [Charlie, DELTA, Foxtrot, alpha, bravo, echo, golf, hotel] You can describe a custom sort ordering by creating a class called a comparator. Copyright 2006 by Pearson Education 12

Comparators n The Comparator interface in java. util describes a method for comparing two objects of a given type: public interface Comparator<T> { public int compare(T o 1, T o 2); } n Note that Comparator is a generic interface. n n T will be replaced by the type of object you are actually comparing. The compare method's job is to decide the relative ordering of the two given objects and return an appropriate integer: n n n <0 0 >0 if o 1 comes before o 2, if o 1 and o 2 are equivalent, if o 1 comes after o 2. Copyright 2006 by Pearson Education 13

Comparator example n The following Comparator compares Strings, ignoring case: public class Case. Insensitive. Comparator implements Comparator<String> { public int compare(String s 1, String s 2) { return s 1. to. Lower. Case(). compare. To( s 2. to. Lower. Case()); } } Copyright 2006 by Pearson Education 14

Sorting with Comparators n The sorting methods shown previously can also be called with a Comparator as a second parameter. n The sorting algorithm will use that comparator to order the elements of the array or list. String[] strings = {"Foxtrot", "alpha", "echo", "golf", "bravo", "hotel", "Charlie", "DELTA"}; Arrays. sort(strings, new Case. Insensitive. Comparator()); System. out. println(Arrays. to. String(strings)); [Charlie, DELTA, Foxtrot, alpha, bravo, echo, golf, hotel] n Output: [alpha, bravo, Charlie, DELTA, echo, Foxtrot, golf, hotel] Copyright 2006 by Pearson Education 15

Program efficiency reading: 13. 2 Copyright 2006 by Pearson Education 16

Efficiency n n efficiency: A measure of the computing resources used by a program, such as time, memory, or disk space. time efficiency: How quickly a program runs n "Fast enough" is often relative to the task being performed. n n n 5 minutes to render a complex 3 D scene for a movie is fast. 5 minutes to search Google is slow. Ways to measure the efficiency of a program: n n empirical analysis: Program the algorithm, run it, and time it. algorithm analysis: Applying techniques to mathematically estimate the algorithm's runtime without actually coding it. Copyright 2006 by Pearson Education 17

Rules for algorithm analysis n n n Most individual statements take 1 unit of time to run. When multiple statements are executed sequentially, their runtimes are added. When statements are executed in a loop, the runtime is multiplied by the number of repetitions of the loop. Copyright 2006 by Pearson Education 18

More examples n n Larger statements can also occur sequentially, in which case their runtimes are added. If larger statements are nested, their runtimes are multiplied. Copyright 2006 by Pearson Education 19

Relative rates of growth n n n most algorithms' runtime can be expressed as a function of the input size N rate of growth: measure of how quickly the graph of a function rises goal: distinguish between fast- and slow-growing functions n n we only care about very large input sizes (for small sizes, most any algorithm is fast enough) this helps us discover which algorithms will run more quickly or slowly, for large input sizes Copyright 2006 by Pearson Education 20

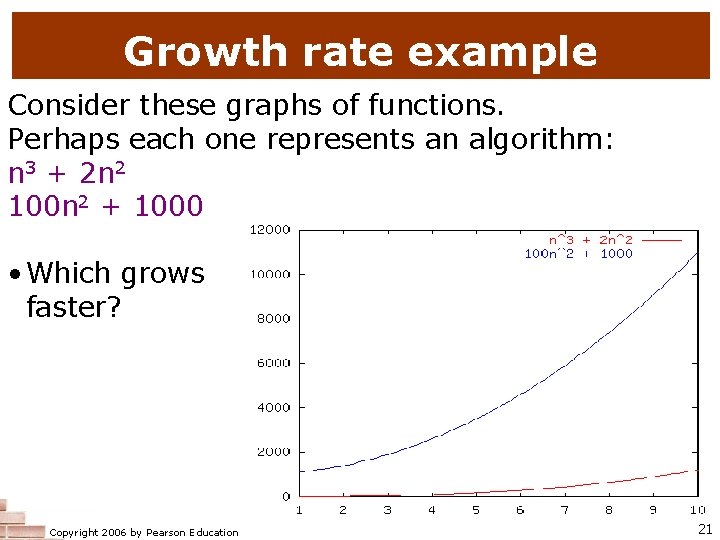
Growth rate example Consider these graphs of functions. Perhaps each one represents an algorithm:

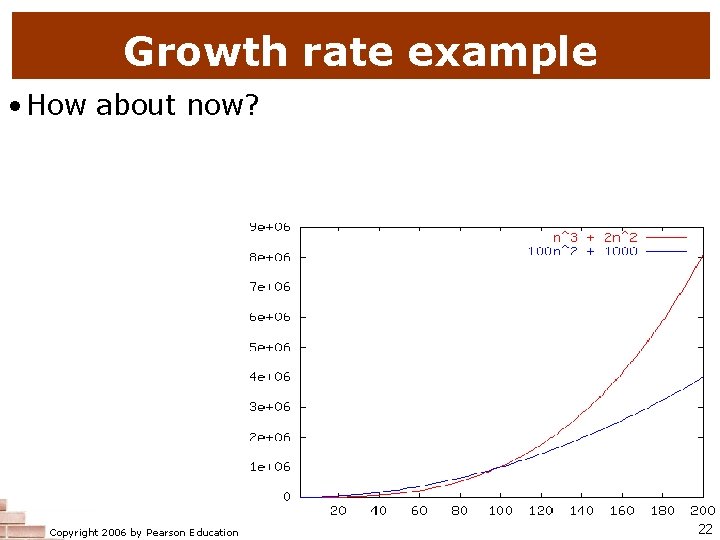
Growth rate example • How about now? Copyright 2006 by Pearson Education 22

Range algorithm 1 n n Let's examine the efficiency and growth rate of three algorithms for finding the range (difference between largest and smallest element) in an array. First algorithm (looks at all pairs of values to find which pair is the largest and smallest): // returns the range of numbers in the given array public static int range(int[] numbers) { int max. Diff = 0; for (int i = 0; i < numbers. length; i++) { for (int j = 0; j < numbers. length; j++) { int diff = Math. abs(numbers[j] - numbers[i]); max. Diff = Math. max(max. Diff, diff); } } return max. Diff; } Copyright 2006 by Pearson Education 23

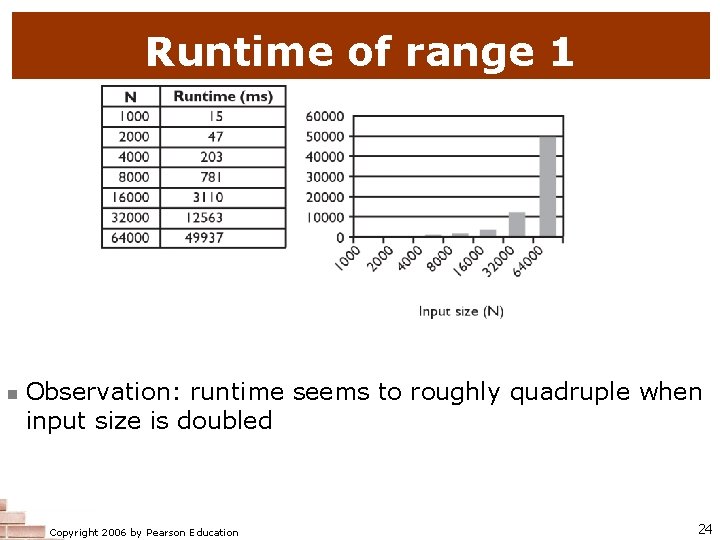
Runtime of range 1 n Observation: runtime seems to roughly quadruple when input size

Range algorithm 2 n n The first algorithm redundantly makes each comparison twice (when i <= j, when i > j). Second, improved algorithm: public static int range 2(int[] numbers) { int max. Diff = 0; for (int i = 0; i < numbers. length; i++) { for (int j = i + 1; j < numbers. length; j++) { int diff = Math. abs(numbers[j] - numbers[i]); max. Diff = Math. max(max. Diff, diff); } } return max. Diff; } Copyright 2006 by Pearson Education 25

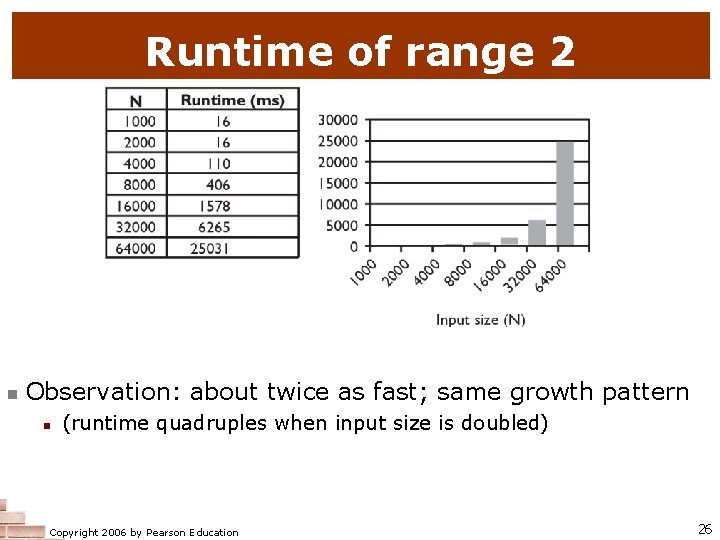
Runtime of range 2 n Observation: about twice as fast; same growth pattern n

Range algorithm 3 n n We can discover the largest and smallest values in a single pass over the array, rather than using many nested passes over all values. Third algorithm: public static int range 3(int[] numbers) { int max = numbers[0]; int min = max; for (int i = 1; i < numbers. length; i++) { if (numbers[i] > max) { max = numbers[i]; } else if (numbers[i] < min) { min = numbers[i]; } } return max - min; } Copyright 2006 by Pearson Education 27

Runtime of range 3 Much faster than others n Runtime doubles when input size

Complexity classes and Big-oh notation reading: 13. 2 Copyright 2006 by Pearson Education 29

Big-Oh notation n complexity class: Category of algorithms' runtime based on relationship to input size. n n Determined by the exponent of the most frequently executed line of code in the algorithm. big-Oh notation: A shorthand for describing complexity classes. n n Example: If the most frequently executed line of an algorithm runs approximately N 3 times, we say the algorithm is "order N 3" or O(N 3) for short. We are concerned with how the function grows when N is large. We are not picky about constant factors. Copyright 2006 by Pearson Education 30

Hierarchy of Big-Oh n Complexity classes in increasing order of growth: n n n n n constant time logarithmic linear loglinear quadratic cubic. . . exponential. . . O(1) O(log N) O(N 2) O(N 3) O(2 N) An algorithm from a lower complexity class will run much faster than one from a higher complexity class when the value of N becomes very large. Copyright 2006 by Pearson Education 31

Program loop runtimes for (int i = 0; i < N; i += c) <statements>; n Adding to the loop counter means that the loop runtime grows linearly when compared to its maximum value N. n Loop executes its body exactly N / c times. for (int i = 0; i < N; i *= c) <statements>; n // O(N) // O(log N) Multiplying the loop counter means that the maximum value N must grow exponentially to linearly increase the loop runtime; therefore, it is logarithmic. n Loop executes its body exactly logc N times. for (int i = 0; i < N * N; i += c) <statements>; n // O(N 2) The loop maximum is N 2, so the runtime is quadratic. n Loop executes its body exactly (N 2 / c) times. Copyright 2006 by Pearson Education 32

More loop runtimes n Nesting loops multiplies their runtimes. for (int i = 0; i < N; i += c) { for (int j = 0; j < N; i += c) { <statements>; } } n // O(N 2) Loops in sequence add together their runtimes, which means the loop set with the larger runtime dominates. for (int i = 0; i < N; i += c) { <statements>; } for (int i = 0; i < N; i += c) { for (int j = 0; j < N; i *= c) { <statements>; } } Copyright 2006 by Pearson Education // O(N) // O(N log N) 33

Loop runtime problems n Approximate the value of the variable sum after the following code fragment, as an expression in terms of input size n. Use Big-Oh notation to describe the algorithm's overall runtime. int sum = 0; for (int i = 1; i <= N; i *= 2) { sum++; } for (int i = 1; i <= 1000; i++) { sum++; } Copyright 2006 by Pearson Education 34

Loop runtime problems n Approximate the value of the variable sum after the following code fragment, as an expression in terms of input size n. Use Big-Oh notation to describe the algorithm's overall runtime. int sum = 0; for (int i = 1; i <= N; i++) { for (int j = 1; j <= i / 2; j += 2) { sum++; } } Copyright 2006 by Pearson Education 35

Implementing binary search reading: 13. 3 Copyright 2006 by Pearson Education 36

Recall: binary search n binary search: An algorithm that searches for a value in a sorted list by repeatedly eliminating half the list from consideration. n n Can be written iteratively or recursively Algorithm pseudocode (searching for a value K): n n Start out with the search area being from indexes 0 to length-1. Examine the element in the middle of the search area. n n If it is K, stop. Otherwise, n n n If it is smaller than K, eliminate the upper half of the search area. If it is larger than K, eliminate the lower half of the search area. Repeat the above examination. Copyright 2006 by Pearson Education 37

Binary search example searching for value 16 0 4 1 7 2 16 3

Binary search example searching for value 16 0 4 min 1 7 mid (too

Binary search pseudocode binary search array a for value i: if all elements have been searched, result is -1. examine middle element a[mid]. if a[mid] equals i, result is mid. if a[mid] is greater than i, binary search lower half of a for i. if a[mid] is less than i, binary search upper half of a for i. Copyright 2006 by Pearson Education 41

Binary search code n The following code implements binary search: // Returns an // appears in // pre: array public static int min = int max = index at which the target the given input array, or -1 if not found. is sorted. int binary. Search(int[] numbers, int target) { 0; numbers. length - 1; while (min <= max) { int mid = (max + min) / 2; if (numbers[mid] == target) { return mid; // found it! } else if (numbers[mid] < target) { min = mid + 1; // too small } else { // numbers[mid] > target max = mid - 1; // too large } } } return -1; Copyright 2006 by Pearson Education // not found 42

Runtime of binary search n n n How do we analyze the runtime of binary search? The algorithm's runtime is dominated by a while loop. Each pass of that loop cuts the search space in half. n How many times does this division in half take place? n n 2 repetitions N repetitions log 2 N Copyright 2006 by Pearson Education 43

Implementing selection sort reading: 13. 3 Copyright 2006 by Pearson Education 44

Selection sort n n selection sort: orders a list of values by repetitively putting a particular value into its final position more specifically: n n n find the smallest value in the list switch it with the value in the first position find the next smallest value in the list switch it with the value in the second position repeat until all values are in their proper places Copyright 2006 by Pearson Education 45

Selection sort example Copyright 2006 by Pearson Education 46

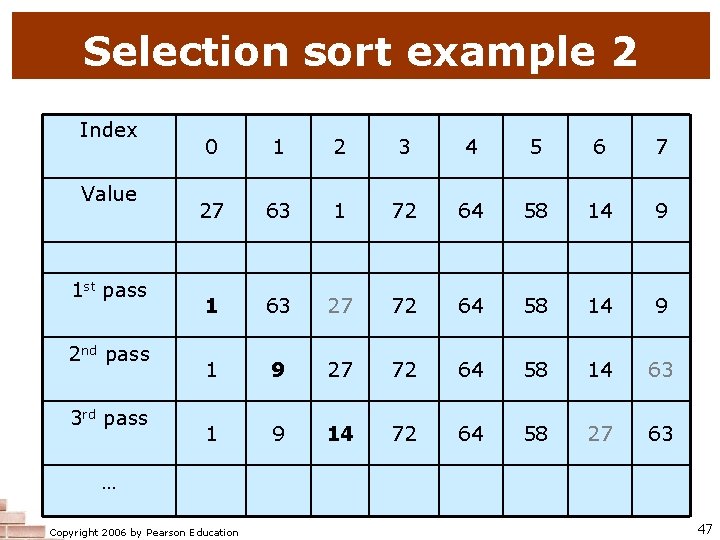
Selection sort example 2 Index Value 1 st pass 2 nd pass 3 rd pass 0 1 2 3 4 5 6 7 27 63 1 72 64 58 14 9 1 63 27 72 64 58 14 9 1 9 27 72 64 58 14 63 1 9 14 72 64 58 27 63 … Copyright 2006 by Pearson Education 47

Selection sort code n The following code implements selection sort: // places elements of the given array into sorted order public static void selection. Sort(int[] a) { for (int i = 0; i < a. length - 1; i++) { // find index of smallest element int smallest = i; for (int j = i + 1; j < a. length; j++) { if (a[j] < a[smallest]) { smallest = j; } } swap(a, i, smallest); // swap smallest to front public static void swap(int[] list, int i, int j) { int temp = list[i]; list[i] = list[j]; list[j] = temp; } Copyright 2006 by Pearson Education 48

Selection sort runtime n Observation: runtime roughly quadruples when input size is doubled n n makes sense because the code performs two nested loops over the array of size N its runtime should be O(N 2) Copyright 2006 by Pearson Education 49

Sorting practice problem n Consider the following array of int values: [22, 11, 34, -5, n 3, 40, 9, 16, 6] Perform the selection sort algorithm on this data. Write the contents of the array after each pass of the outermost loop of selection sort until the array is sorted. Copyright 2006 by Pearson Education 50

Implementing merge sort reading: 13. 4 Copyright 2006 by Pearson Education 51

Merge sort n merge sort: orders a list of values by recursively dividing the list in half until each sub-list has one element, then recombining n n n Invented by John von Neumann in 1945 relies on observation that if you have two sorted lists of values, they can be combined into a single larger sorted list quickly merge sort pseudocode: n n split the array into two halves. merge sort the left half (recursively). merge sort the right half (recursively). combine the two halves into a sorted whole. Copyright 2006 by Pearson Education 52

Merge sort example 98 23 45 14 98 23 98 45 14 23 45

Merge sort example 2 13 6 21 18 9 4 8 20 0 7 13 6 21 0 18 9 3 4 4 8 20 7 13 6 21 18 9 4 8 20 0 1 2 3 4 5 6 7 6 13 18 21 4 9 8 20 0 1 2 3 4 5 6 7 18 21 4 8 3 4 6 13 0 4 6 0 Copyright 2006 by Pearson Education 8 9 13 9 20 7 18 20 21 7 54

Merging two sorted arrays n merge operation: n Given two sorted arrays, merge operation produces a sorted array with all the elements of the two arrays A 6 C n 13 4 18 6 21 8 9 B 4 8 9 13 18 20 21 20 Running time of merge : O(N), where N is the number of elements in the merged array. n When merging two sorted parts of the same array, we'll need a temporary array to store the merged whole. Copyright 2006 by Pearson Education 55

Merge operation example Copyright 2006 by Pearson Education 56

Split into halves code n The following code splits an array into its two halves: // Returns the first half of the given array. public static int[] left. Half(int[] array) { int size 1 = array. length / 2; int[] left = new int[size 1]; for (int i = 0; i < size 1; i++) { left[i] = array[i]; } return left; } // Returns the second half of the given array. public static int[] right. Half(int[] array) { int size 1 = array. length / 2; int size 2 = array. length - size 1; int[] right = new int[size 2]; for (int i = 0; i < size 2; i++) { right[i] = array[i + size 1]; } return right; } Copyright 2006 by Pearson Education 57

Merge code n The following code implements the merge operation // pre : result is empty; left/right are sorted // post: result contains merged sorted lists. public static void merge(int[] result, int[] left, int[] right) { int i 1 = 0; // index into left array int i 2 = 0; // index into right array for (int i = 0; i < result. length; i++) { if (i 2 >= right. length || (i 1 < left. length && left[i 1] <= right[i 2])) { result[i] = left[i 1]; // take from left i 1++; } else { result[i] = right[i 2]; // take from right i 2++; } } } Copyright 2006 by Pearson Education 58

Merge sort code n The following code implements the overall merge sort: // Places elements of given array into sorted order // using the merge sort algorithm. public static void merge. Sort(int[] array) { if (array. length > 1) { // split array into two halves int[] left = left. Half(array); int[] right = right. Half(array); // recursively sort the two halves merge. Sort(left); merge. Sort(right); } } // merge the sorted halves into a sorted whole merge(array, left, right); Copyright 2006 by Pearson Education 59

Sorting practice problem n Consider the following array of int values. [22, 11, 34, -5, n 3, 40, 9, 16, 6] Perform the merge sort algorithm on this data. Write the contents of the array after each of the recursive calls of merge sort have finished. Copyright 2006 by Pearson Education 60