Building Foundations for Mathematics CONCEPTUAL UNDERSTANDING OF FRACTIONS

Building Foundations for Mathematics CONCEPTUAL UNDERSTANDING OF FRACTIONS

Estimate how much pie was eaten?

Using Fraction Models • Student proficiency with fractions is essential to success in algebra • Models help students clarify ideas that are often confused in a purely symbolic mode • Students need many concrete experiences with fractions to develop a deep understanding • The process should be introduced by using visual fraction models (area models, number lines, and so on) to build understanding before moving into the standard algorithm • Important to do the same activity using two different types of models

Using Fraction Models • Introduce multiple models for the same fraction. It is important that students don’t get stuck using only one model for a given fraction. Having multiple models at their disposal will help the flexibility of their thinking and allow them to switch models if needed. • Encourage students to think flexibly about “the whole”. When working with the set model, students see that ¼ looks different in a set of 4 items than it does in a set of 12 items. • Allow students to explore fractions as more than just “a part of a whole”. • Give students practice with decomposing fractions. • Estimate! When introducing new fractions that are unfamiliar to students, help them rely on benchmarks (0, ½, and 1). http: //www. cehd. umn. edu/ci/rationalnumberproject/default. html

Conceptual Models Region: a whole which has been partitioned into equal parts and some of those parts are shaded. Linear: length of the whole is divided into equal lengths (easily connected to fractions on a number line) Set: a set of objects as a whole (unit). Work very well for developing algorithms later on. Area: rectangles to show a visual representation of the product of two fractions

Region Models Region: a whole which has been partitioned into equal parts and some of those parts are shaded. • • • The most concrete model and most often used. The region is the whole (the unit) and the parts are congruent (same shape and size) When presenting the region model a variety of shapes should be used so students don’t always think of fractions as piece of a pie. The rectangle is the easiest model for children to draw and partition. The circle is easiest to see as a whole.

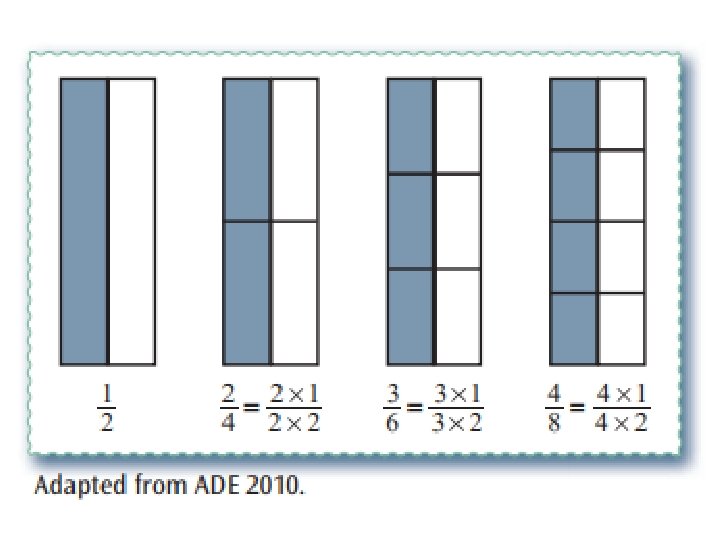
Try It … •

Table Talk How does using the region model support student conceptual understanding?

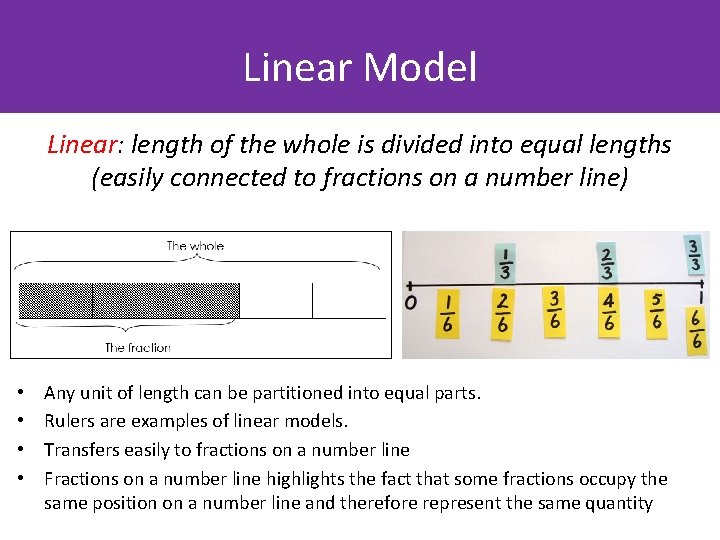
Linear Model Linear: length of the whole is divided into equal lengths (easily connected to fractions on a number line) • • Any unit of length can be partitioned into equal parts. Rulers are examples of linear models. Transfers easily to fractions on a number line Fractions on a number line highlights the fact that some fractions occupy the same position on a number line and therefore represent the same quantity

Try It … •

Table Talk How does using the linear model support student conceptual understanding?

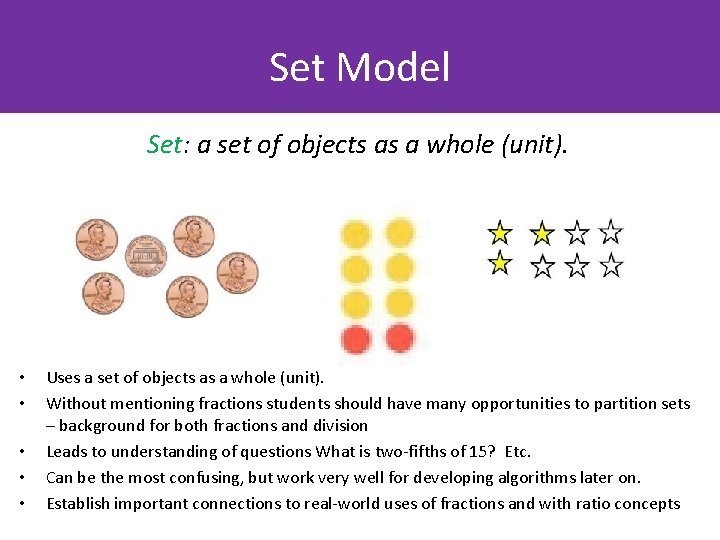
Set Model Set: a set of objects as a whole (unit). • • • Uses a set of objects as a whole (unit). Without mentioning fractions students should have many opportunities to partition sets – background for both fractions and division Leads to understanding of questions What is two-fifths of 15? Etc. Can be the most confusing, but work very well for developing algorithms later on. Establish important connections to real-world uses of fractions and with ratio concepts

Using the manipulatives … •

Table Talk How does using the set model support student conceptual understanding?

Area Model Area: rectangles to show a visual representation of the product of two fractions

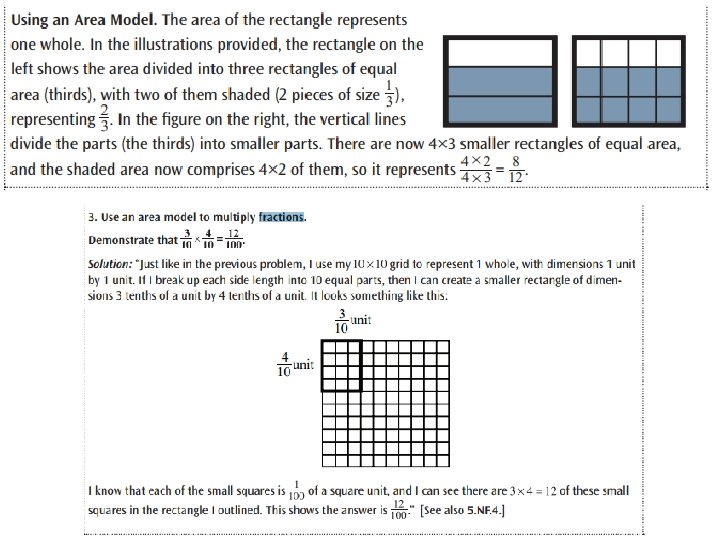
Try It … •

Table Talk How does using the area model support student conceptual understanding?

Subitizing with Fractions www. buildmathminds. com/fof-free

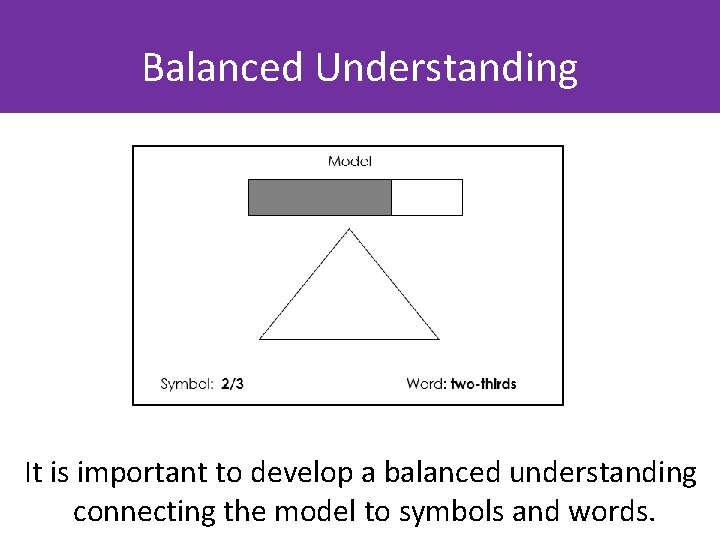
Balanced Understanding It is important to develop a balanced understanding connecting the model to symbols and words.

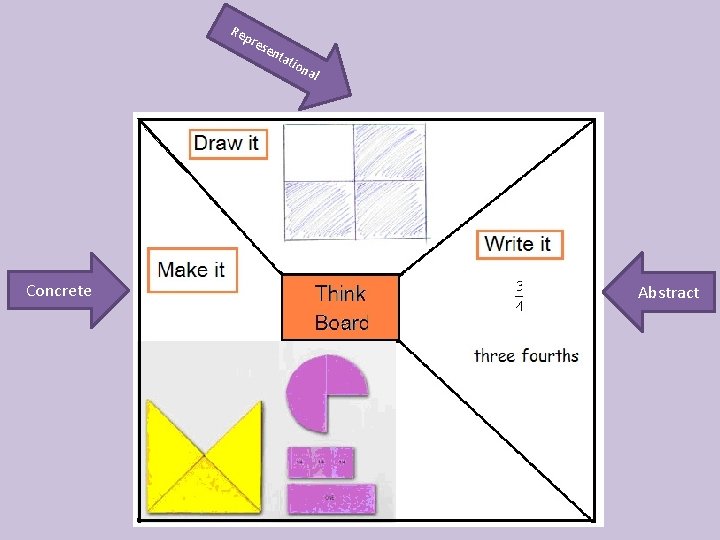
Re pr Concrete ese nta t ion al Abstract

Final Thought Convince your partner of the value of using a variety of fraction models for student conceptual understanding.