Bubble Sort Sorting S Computers only use numeric

Bubble Sort

Sorting S Computers only use numeric values for sorting S Does this mean you cannot sort a file by a character field (such as last name or state)? S No, it doesn’t. The computer converts all characters into a series of 0’s and 1’s. It’s the 0’s and 1’s that the computer uses to compare fields for sorting. S You can sort a file by S ascending order (lowest to highest) S descending order (highest to lowest)

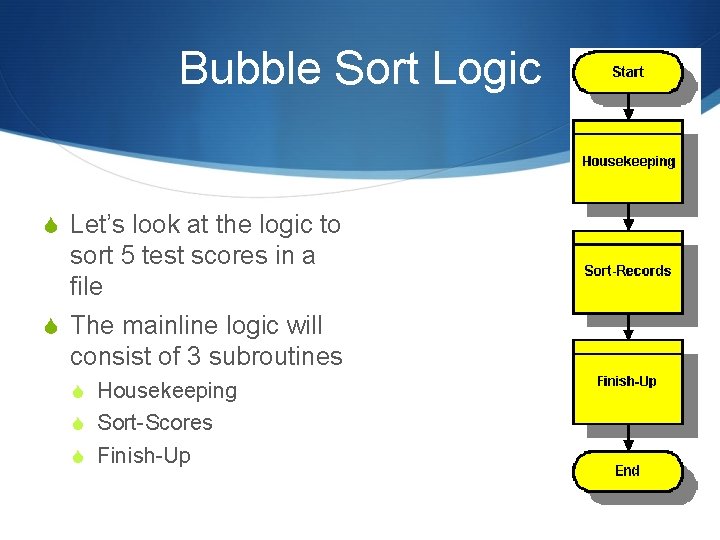
Bubble Sort Logic S Let’s look at the logic to sort 5 test scores in a file S The mainline logic will consist of 3 subroutines S Housekeeping S Sort-Scores S Finish-Up

Starting the Sort-Scores Routine S When Housekeeping is done, the five scores from the In-Score file are in the Score array. S Let’s assume the scores are: Score(1) = 90 Score(2) = 85 Score(3) = 65 Score(4) = 95 Score(5) = 75 • The next slide shows the start of the routine

Swapping Scores S To start the sort, the first two values in the array are compared. • If they are out of ascending order, switch (or swap) their positions in the array • The order is a little better than before Score(1) = 90 Score(2) = 85 Score(3) = 65 Score(4) = 95 Score(5) = 75 Score(1) = 85 Score(2) = 90 Score(3) = 65 Score(4) = 95 Score(5) = 75

Swapping Dilemma S Here is our original score array S If we move the value 90 from Score(1) to Score(2), S both array elements would contain the value 90 S the value 85 would be lost S If you move 85 to Score(1), then the value 90 would be lost S How can we solve this problem? Score(1) = 90 Score(2) = 85 Score(3) = 65 Score(4) = 95 Score(5) = 75

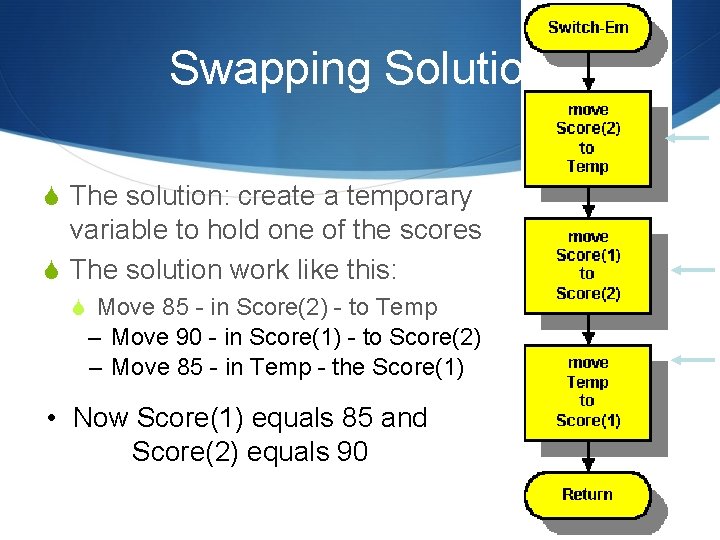
Swapping Solution S The solution: create a temporary variable to hold one of the scores S The solution work like this: S Move 85 - in Score(2) - to Temp – Move 90 - in Score(1) - to Score(2) – Move 85 - in Temp - the Score(1) • Now Score(1) equals 85 and Score(2) equals 90

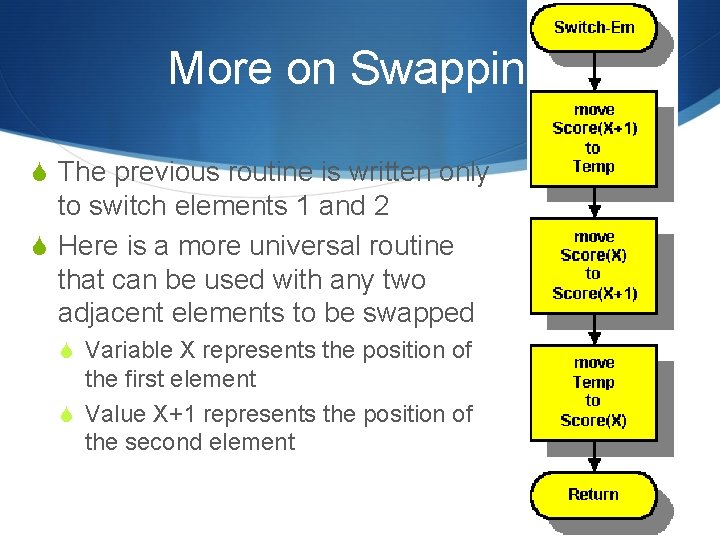
More on Swapping S The previous routine is written only to switch elements 1 and 2 S Here is a more universal routine that can be used with any two adjacent elements to be swapped S Variable X represents the position of the first element S Value X+1 represents the position of the second element

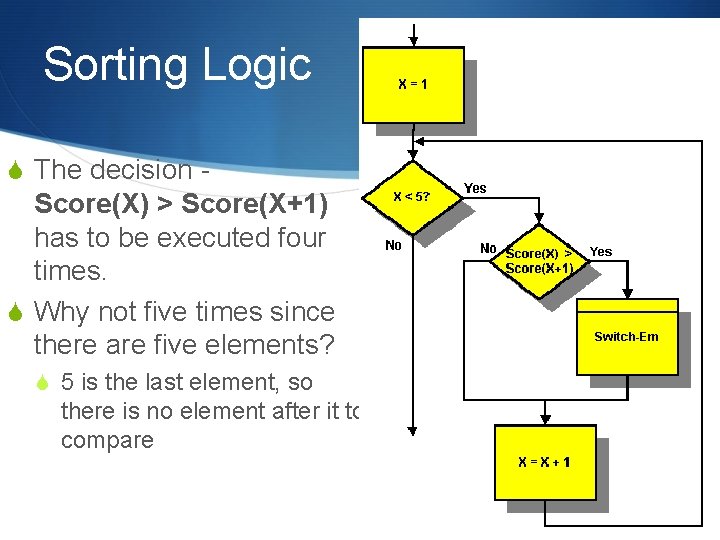
Sorting Logic S The decision - Score(X) > Score(X+1) has to be executed four times. S Why not five times since there are five elements? S 5 is the last element, so there is no element after it to compare

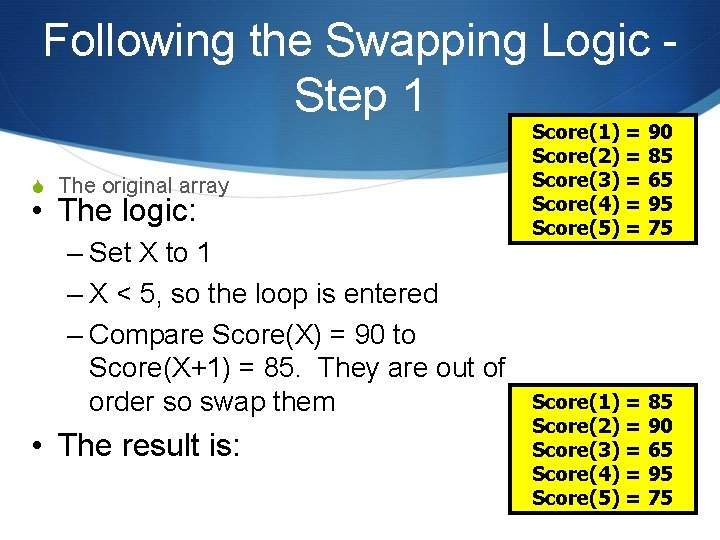
Following the Swapping Logic Step 1 S The original array • The logic: – Set X to 1 – X < 5, so the loop is entered – Compare Score(X) = 90 to Score(X+1) = 85. They are out of order so swap them • The result is: Score(1) = 90 Score(2) = 85 Score(3) = 65 Score(4) = 95 Score(5) = 75 Score(1) = 85 Score(2) = 90 Score(3) = 65 Score(4) = 95 Score(5) = 75

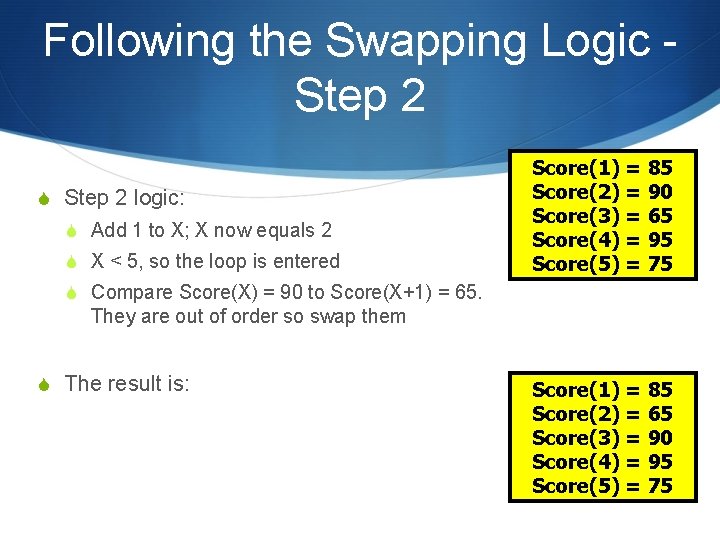
Following the Swapping Logic Step 2 S Step 2 logic: S Add 1 to X; X now equals 2 S X < 5, so the loop is entered Score(1) = 85 Score(2) = 90 Score(3) = 65 Score(4) = 95 Score(5) = 75 S Compare Score(X) = 90 to Score(X+1) = 65. They are out of order so swap them S The result is: Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 95 Score(5) = 75

Following the Swapping Logic Step 3 S Step 3 logic: S Add 1 to X; X now equals 3 S X < 5, so the loop is entered Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 95 Score(5) = 75 S Compare Score(X) = 90 to Score(X+1) = 95. They are in order. No swap is made S The result is: Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 95 Score(5) = 75

Following the Swapping Logic Step 4 S Step 4 logic: Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 95 Score(5) = 75 S Add 1 to X; X now equals 4 S X < 5, so the loop is entered S Compare Score(X) = 95 to Score(X+1) = 75. They are out of order so swap them S The result is: Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 75 Score(5) = 95

Following the Swapping Logic Step 5 S Step 5 logic: S Add 1 to X; X now equals 5 S X = 5, so the loop is not entered and the Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 75 Score(5) = 95 swapping logic is completed S Every element has been compared to the one adjacent to it • The largest amount (95) has sunk to the bottom of the list

Continuing the Swapping Logic S Although the list is in a better ascending order, it is still not in order Score(1) = 85 Score(2) = 65 Score(3) = 90 Score(4) = 75 Score(5) = 95 S The five steps need to be performed again so the following values will swap places S 85 and 65 S 90 and 75 Score(1) = 65 Score(2) = 85 Score(3) = 75 Score(4) = 90 Score(5) = 95

Continuing the Swapping Logic S The five steps will need to be performed one more time to swap 85 and 75 Score(1) = 65 Score(2) = 85 Score(3) = 75 Score(4) = 90 Score(5) = 95 S The final result Score(1) = 65 Score(2) = 75 Score(3) = 85 Score(4) = 90 Score(5) = 95

If the list were in the worst possible order. . S The five steps would have to be performed four time to get the list in correct ascending order Score(1) = 95 Score(2) = 90 Score(3) = 85 Score(4) = 75 Score(5) = 65 To go from this list to this list Have to pass through the loop 4 times Score(1) = 65 Score(2) = 75 Score(3) = 85 Score(4) = 90 Score(5) = 95

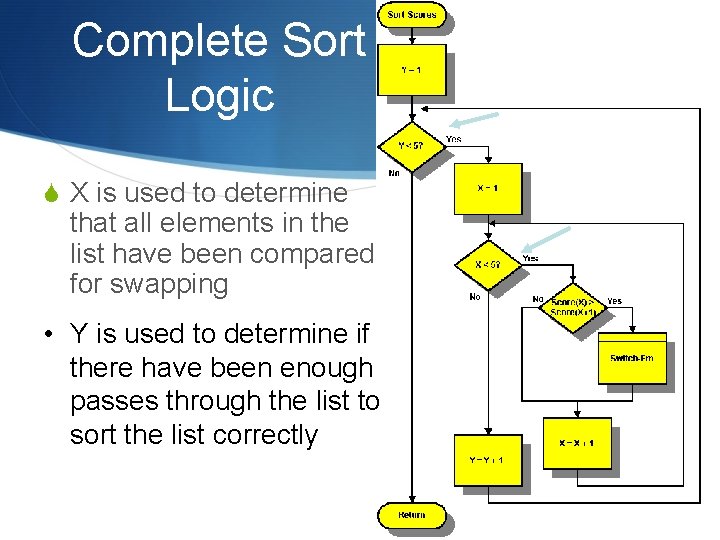
Complete Sort Logic S X is used to determine that all elements in the list have been compared for swapping • Y is used to determine if there have been enough passes through the list to sort the list correctly

More on Bubble Sorts S Using a variable for the array size S Previously, a constant (5) was used to determine the end of loop processing S Using a variable means the code doesn’t change if the size of the array changes

Rules for Sorting S The greatest number of pair comparisons needed to be made during each loop is one fewer than the number of elements is the array S The pair comparison loop needs to be processed one time fewer than the number of elements in the array

Reducing Unnecessary Comparisons S In a bubble sort, the first pass through the list guarantees the last item on the list will be at the bottom S For second pass, the second to the last item will be in the correct position S Each pass will correctly place an item towards the bottom of the list S When performing each pass, why continue to compare items known to be correct?

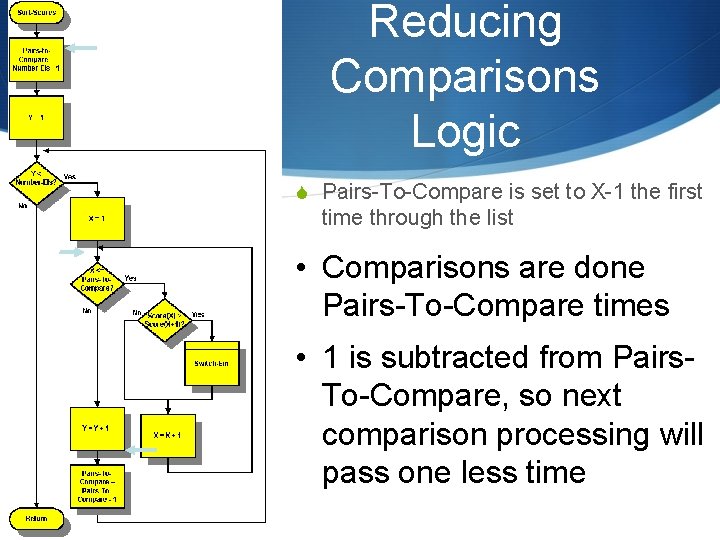
Reducing Comparisons Logic S Pairs-To-Compare is set to X-1 the first time through the list • Comparisons are done Pairs-To-Compare times • 1 is subtracted from Pairs. To-Compare, so next comparison processing will pass one less time

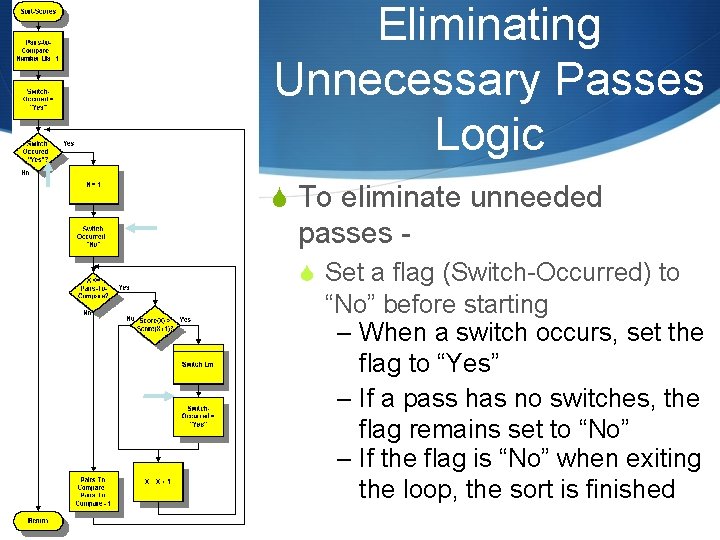
Eliminating Unnecessary Passes Logic S To eliminate unneeded passes S Set a flag (Switch-Occurred) to “No” before starting – When a switch occurs, set the flag to “Yes” – If a pass has no switches, the flag remains set to “No” – If the flag is “No” when exiting the loop, the sort is finished