BU 520 601 Decision Models Decision Analysis Decision

BU. 520. 601 Decision Models Decision Analysis Decision. Analysis Summer 2013 BU. 520. 601 1

§ Let us flip a fair coin once (there is a fee). If you win I give you $102. If I win, you give me $100. How much fee will you pay me for playing the game: $5, $2, $1, $0? You can select any other amount. § Let us flip a fair coin 1000 (there is a fee). If you win a toss, I give you $102. If I win, you give me $100. How much fee will you pay for the playing the entire game? Suppose you are getting ready to go the office in a crowded metro. Carrying an umbrella is a hassle; you will carry it only when you feel necessary. Forecast for today is 70% chance of rain and the sky is overcast. Should you carry an umbrella - Yes or no? My decision would be “Yes” and it is a good decision. However, there are two possible outcomes - it will rain or not. If it does not rain, it does not mean I have made a bad decision. Decision. Analysis BU. 520. 601 2

Decision Analysis (DA) • • • DA is a methodology applicable to analyze a wide variety of problems. Although DA was used in the 1950 s (at Du Pont) and early 1960 s (at Pillsbury), major DA development took place in mid sixties. One of the earliest application (at GE) was to analyze whether a super heater should be added to the current power reactor. DA has been considered as a technology to assist (individuals and) organizations in decision making by quantifying the considerations (even though they may be subjective) to deduce logical actions. Decision. Analysis BU. 520. 601 3

Decision Analysis (DA) One can discuss many topics listed below; we will look at a few. • Problem Formulation. • Decision Making with / without Probabilities. • Risk Analysis and Sensitivity Analysis. • Decision Analysis with Sample / Perfect Information. • Multistage decision making. Tools and terminology • Basic statistics and probability • Influence diagram / payoff table / decision tree • EMV: Expected Monetary Value • EVSI / EVPI : Expected Value of Sample / Perfect Information Decision. Analysis BU. 520. 601 • • • Bayes’ rule Decision vs. outcome Risk management Minimax / maximin / Utility theory 4
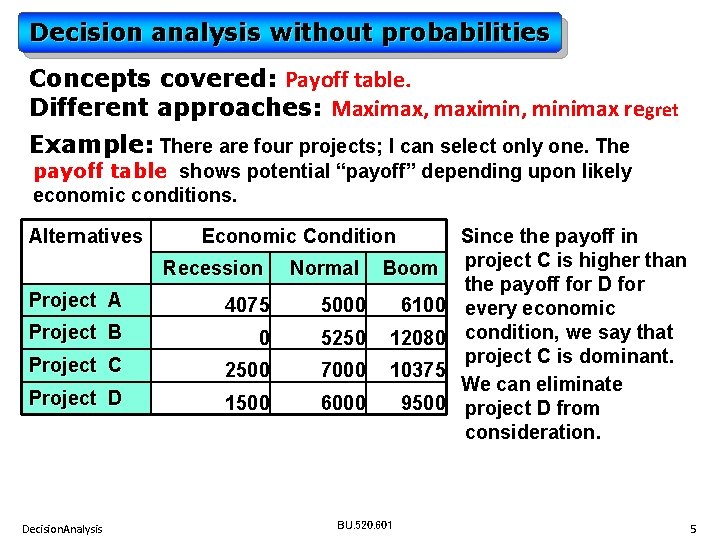
Decision analysis without probabilities Concepts covered: Payoff table. Different approaches: Maximax, maximin, minimax regret Example: There are four projects; I can select only one. The payoff table shows potential “payoff” depending upon likely economic conditions. Alternatives Economic Condition Recession Normal Boom Project A 4075 5000 6100 Project B 0 5250 12080 Project C 2500 7000 10375 Project D 1500 6000 9500 Decision. Analysis BU. 520. 601 Since the payoff in project C is higher than the payoff for D for every economic condition, we say that project C is dominant. We can eliminate project D from consideration. 5
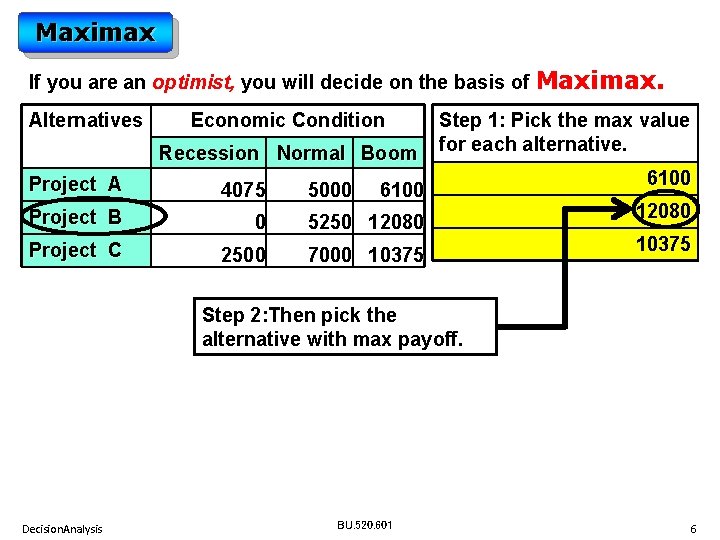
Maximax If you are an optimist, you will decide on the basis of Maximax. Alternatives Economic Condition Recession Normal Boom Project A 4075 Project B 0 5250 12080 Project C 2500 7000 10375 5000 Step 1: Pick the max value for each alternative. 6100 12080 10375 Step 2: Then pick the alternative with max payoff. Decision. Analysis BU. 520. 601 6

Maximin If you are a conservative you will use Maximin. Alternatives Economic Condition Recession Normal Boom 1: Pick the min value for each alternative. Project A 4075 5000 6100 4075 Project B 0 5250 12080 0 Project C 2500 7000 10375 2500 2: Then pick the alternative with max payoff. Decision. Analysis BU. 520. 601 7
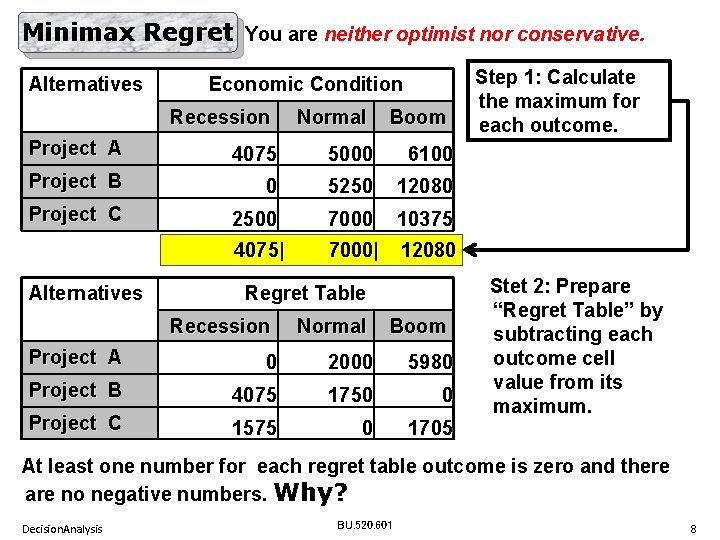
Minimax Regret You are neither optimist nor conservative. Alternatives Economic Condition Recession Normal Boom Project A 4075 5000 6100 Project B 0 5250 12080 Project C 2500 7000 10375 4075| 7000| 12080 Alternatives Regret Table Recession Normal Boom Project A 0 2000 5980 Project B 4075 1750 0 Project C 1575 0 1705 Step 1: Calculate the maximum for each outcome. Stet 2: Prepare “Regret Table” by subtracting each outcome cell value from its maximum. At least one number for each regret table outcome is zero and there are no negative numbers. Why? Decision. Analysis BU. 520. 601 8
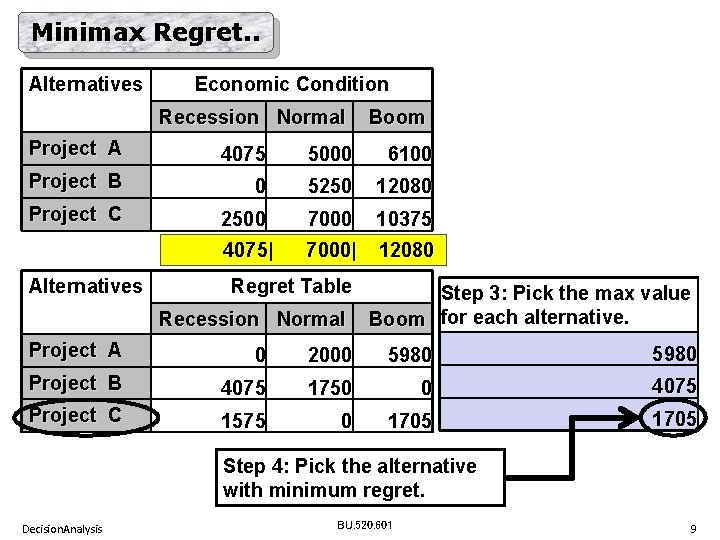
Minimax Regret. . Alternatives Economic Condition Recession Normal Boom Project A 4075 5000 6100 Project B 0 5250 12080 Project C 2500 7000 10375 4075| 7000| 12080 Alternatives Regret Table Recession Normal Step 3: Pick the max value Boom for each alternative. Project A 0 2000 5980 Project B 4075 1750 0 4075 Project C 1575 0 1705 Step 4: Pick the alternative with minimum regret. Decision. Analysis BU. 520. 601 9

General comments Payoff table Alternatives Table columns show outcomes (also called state of nature). Economic Condition Recession Normal Boom Project A 4075 Project B 0 5250 12080 Project C 2500 7000 10375 5000 6100 • The maximax payoff criterion seeks the largest of the maximum payoffs among the actions. • The maximin payoff criterion seeks the largest of the minimum payoffs among the actions. • The minimax regret criterion seeks the smallest of the maximum regrets among the actions. The above three approaches we used involved Decision Making without Probabilities. Decision. Analysis BU. 520. 601 10
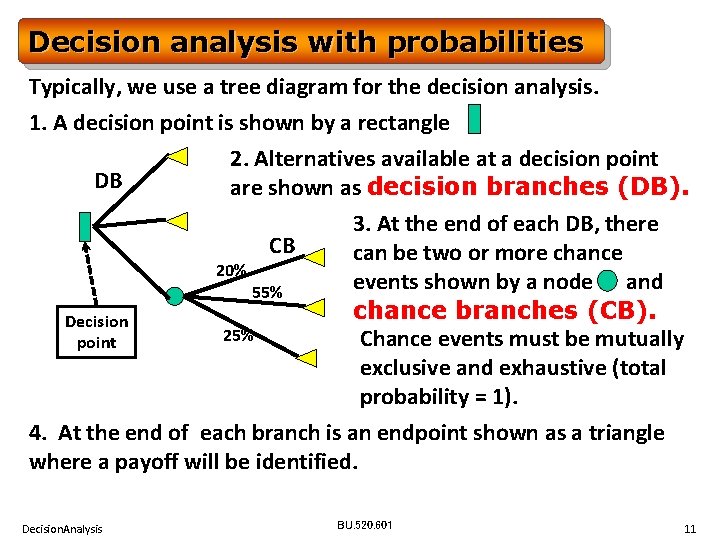
Decision analysis with probabilities Typically, we use a tree diagram for the decision analysis. 1. A decision point is shown by a rectangle 2. Alternatives available at a decision point DB are shown as decision branches (DB). 3. At the end of each DB, there CB can be two or more chance 20% events shown by a node and 55% chance branches (CB). Decision 25% Chance events must be mutually point exclusive and exhaustive (total probability = 1). 4. At the end of each branch is an endpoint shown as a triangle where a payoff will be identified. Decision. Analysis BU. 520. 601 11
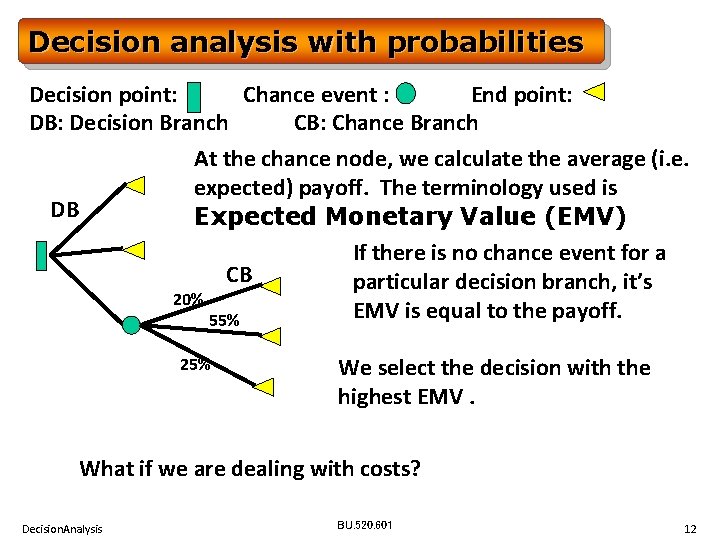
Decision analysis with probabilities Decision point: Chance event : End point: DB: Decision Branch CB: Chance Branch At the chance node, we calculate the average (i. e. expected) payoff. The terminology used is DB Expected Monetary Value (EMV) If there is no chance event for a CB particular decision branch, it’s 20% EMV is equal to the payoff. 55% 25% We select the decision with the highest EMV. What if we are dealing with costs? Decision. Analysis BU. 520. 601 12
A larger tree diagram Decision. Analysis BU. 520. 601 13

Example 1 You bought 500 units of X @$10 each. A dealer has offered to buy these from you @$14 each ( you can make $4/unit profit). You can sell these yourself for $16 Demand: X 300 400 500 600 each ($6/unit profit) but the 0. 30 0. 45 0. 20 0. 05 demand is uncertain. The demand Pr(X) distribution is shown in the table. Obviously, if demand exceeds 500, you will sell all 500. On the other hand, if demand is under 500, you will have leftover units. These leftover items can disposed off for $7 each ($3 loss, the dealer will no longer buy these leftover units from you). What’s your decision? Decision. Analysis BU. 520. 601 14

Example 1. . Suppose you have 500 units of X in Demand: X 300 400 500 600 stock, purchased for $10 each. Dealer Pr(X) 0. 30 0. 45 0. 20 0. 05 sales price: $14, self sale price: $16 with salvage value: $7. Start with the tree having 2 branches (DB) at the decision point. There are no chance events in the dealer sale branch, For the self sale, there are 4 mutually exclusive possibilities. Dealer Sale Self sale % 0 3 , 0 45% , 30 0 0 4 500, 20% 600 , 5% Decision. Analysis BU. 520. 601 15
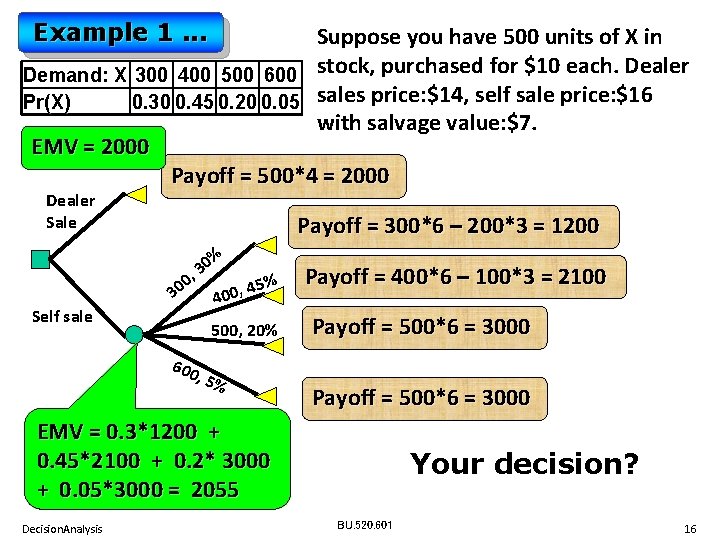
Example 1. . . Suppose you have 500 units of X in Demand: X 300 400 500 600 stock, purchased for $10 each. Dealer Pr(X) 0. 30 0. 45 0. 20 0. 05 sales price: $14, self sale price: $16 with salvage value: $7. EMV = 2000 Payoff = 500*4 = 2000 Dealer Sale Self sale Payoff = 300*6 – 200*3 = 1200 % 0 3 , 0 45% , 30 0 0 4 500, 20% 600 , 5% Payoff = 400*6 – 100*3 = 2100 Payoff = 500*6 = 3000 EMV = 0. 3*1200 + 0. 45*2100 + 0. 2* 3000 + 0. 05*3000 = 2055 Decision. Analysis Your decision? BU. 520. 601 16
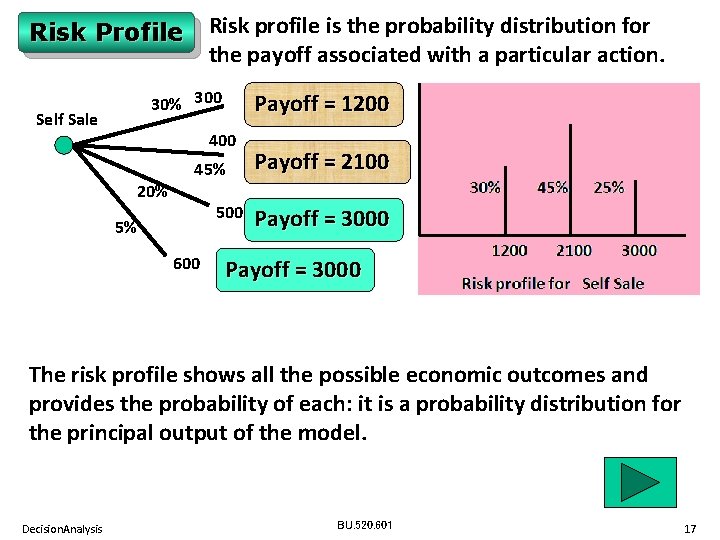
Risk profile is the probability distribution for the payoff associated with a particular action. Risk Profile 30% 300 Self Sale Payoff = 1200 400 20% 45% 500 5% 600 Payoff = 2100 Payoff = 3000 The risk profile shows all the possible economic outcomes and provides the probability of each: it is a probability distribution for the principal output of the model. Decision. Analysis BU. 520. 601 17

Example 3 We have received RFP (Request For Proposal). • We may not want to bid at all (our cost: 0) • If we bid, we will have to spend $5 k for proposal preparation. Based on the information provided in the RFP, a quick decision is to bid either $115 k or $120 k or $125 k. We must select among 4 alternatives (including no bid). • A quick estimate of the cost of the project (in addition to the preparation cost) is $95 k. • Looks like we may have a competitor. • If we bid the same amount as the competitor, we will get the project because of our reputation with the client. • We have gathered some probabilities based on past experience. Decision. Analysis BU. 520. 601 18
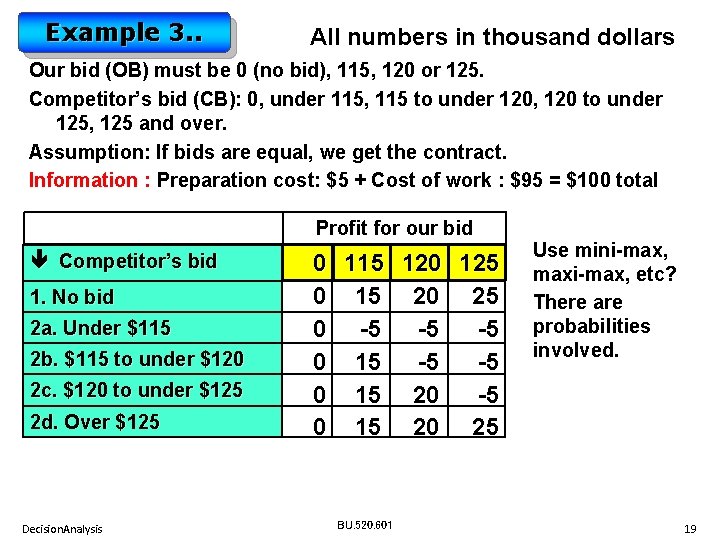
Example 3. . All numbers in thousand dollars Our bid (OB) must be 0 (no bid), 115, 120 or 125. Competitor’s bid (CB): 0, under 115, 115 to under 120, 120 to under 125, 125 and over. Assumption: If bids are equal, we get the contract. Information : Preparation cost: $5 + Cost of work : $95 = $100 total Profit for our bid Competitor’s bid 1. No bid 2 a. Under $115 2 b. $115 to under $120 2 c. $120 to under $125 2 d. Over $125 Decision. Analysis 0 115 120 125 0 15 20 25 0 -5 -5 -5 0 15 20 25 BU. 520. 601 Use mini-max, maxi-max, etc? There are probabilities involved. 19
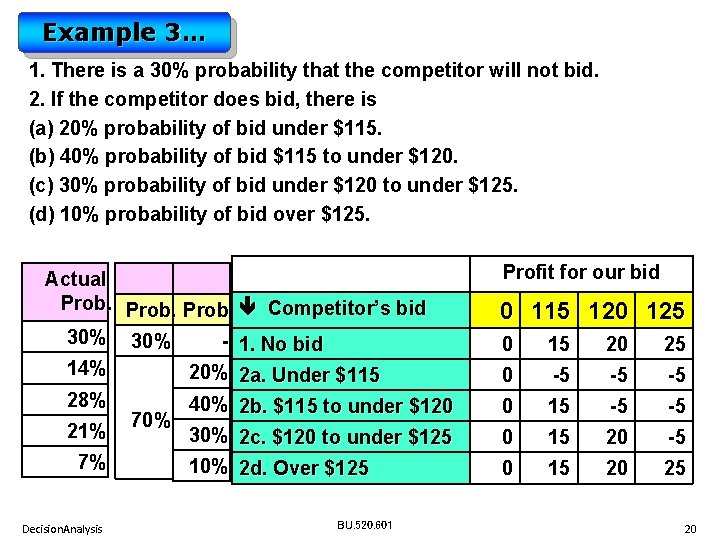
Example 3… 1. There is a 30% probability that the competitor will not bid. 2. If the competitor does bid, there is (a) 20% probability of bid under $115. (b) 40% probability of bid $115 to under $120. (c) 30% probability of bid under $120 to under $125. (d) 10% probability of bid over $125. Actual Prob. Competitor’s bid 30% - 1. No bid 14% 28% 21% 7% Decision. Analysis 70% Profit for our bid 0 115 120 125 0 15 20 25 20% 2 a. Under $115 40% 2 b. $115 to under $120 0 -5 -5 -5 0 15 -5 -5 30% 2 c. $120 to under $125 10% 2 d. Over $125 0 15 20 -5 0 15 20 25 BU. 520. 601 20
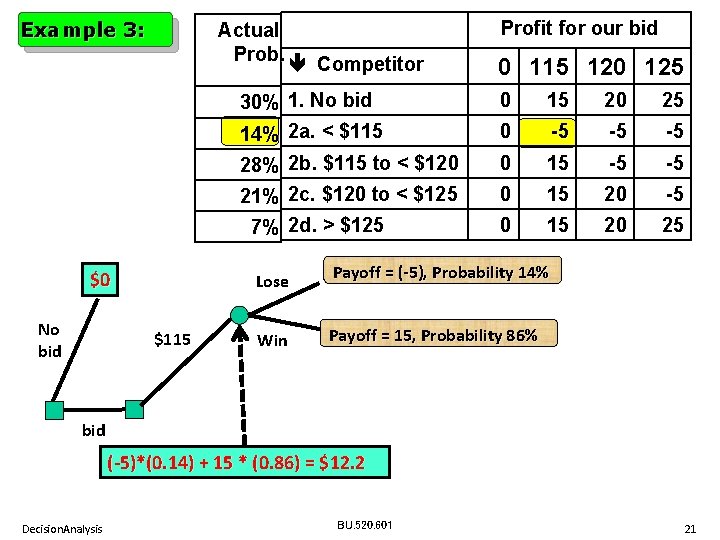
Example 3: Actual Prob. Competitor No bid $115 0 115 120 125 30% 1. No bid 14% 2 a. < $115 0 15 20 25 0 -5 -5 -5 28% 2 b. $115 to < $120 21% 2 c. $120 to < $125 0 15 -5 -5 0 15 20 25 7% 2 d. > $125 $0 Profit for our bid Lose Payoff = (-5), Probability 14% Win Payoff = 15, Probability 86% bid (-5)*(0. 14) + 15 * (0. 86) = $12. 2 Decision. Analysis BU. 520. 601 21
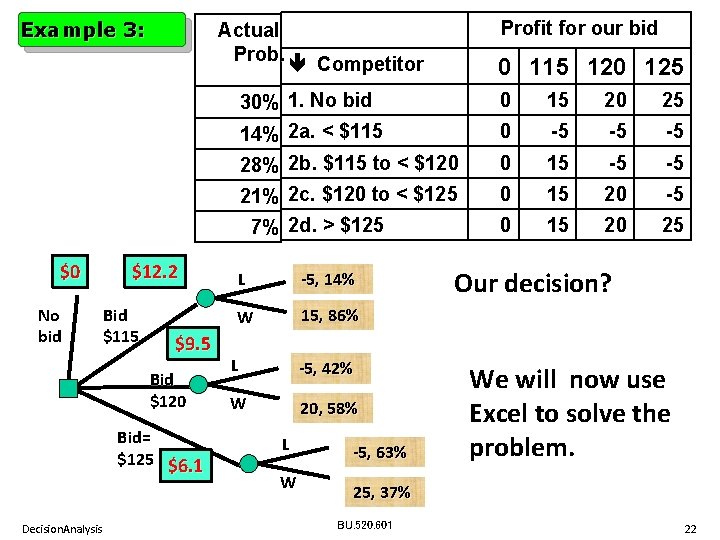
Example 3: No bid $12. 2 Bid $115 $9. 5 Bid $120 Bid= $125 $6. 1 Decision. Analysis 0 115 120 125 30% 1. No bid 14% 2 a. < $115 0 15 20 25 0 -5 -5 -5 28% 2 b. $115 to < $120 21% 2 c. $120 to < $125 0 15 -5 -5 0 15 20 25 7% 2 d. > $125 $0 Profit for our bid Actual Prob. Competitor L -5, 14% W 15, 86% L -5, 42% W 20, 58% L W -5, 63% Our decision? We will now use Excel to solve the problem. 25, 37% BU. 520. 601 22
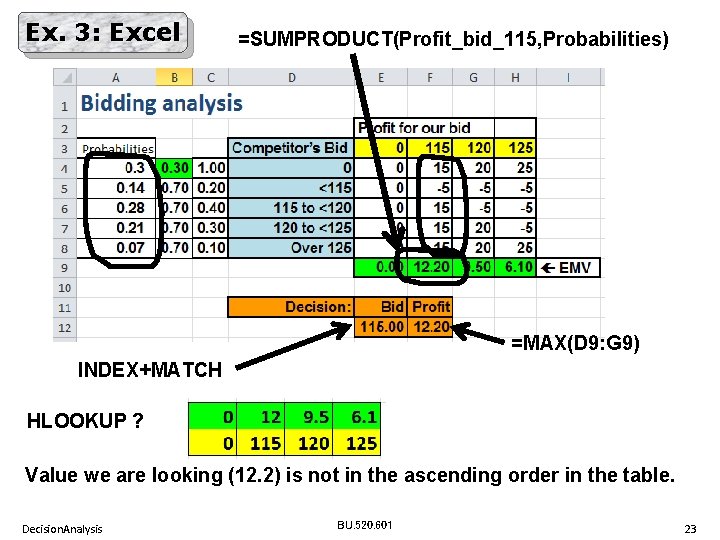
Ex. 3: Excel =SUMPRODUCT(Profit_bid_115, Probabilities) =MAX(D 9: G 9) INDEX+MATCH HLOOKUP ? Value we are looking (12. 2) is not in the ascending order in the table. Decision. Analysis BU. 520. 601 23
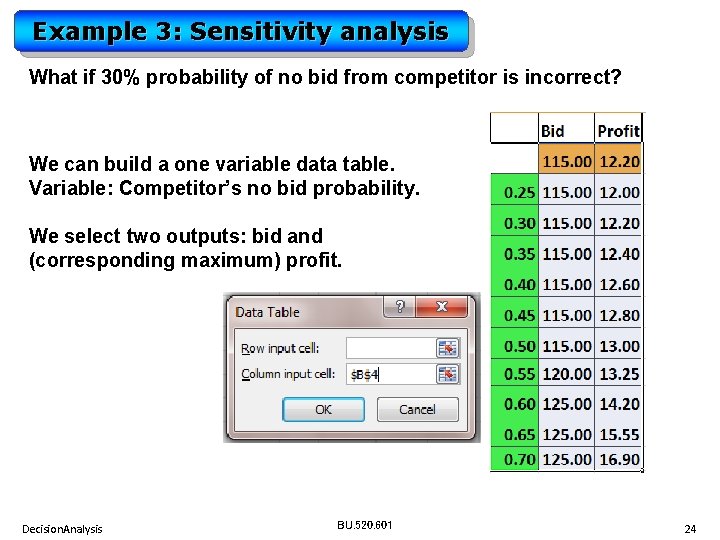
Example 3: Sensitivity analysis What if 30% probability of no bid from competitor is incorrect? We can build a one variable data table. Variable: Competitor’s no bid probability. We select two outputs: bid and (corresponding maximum) profit. Decision. Analysis BU. 520. 601 24
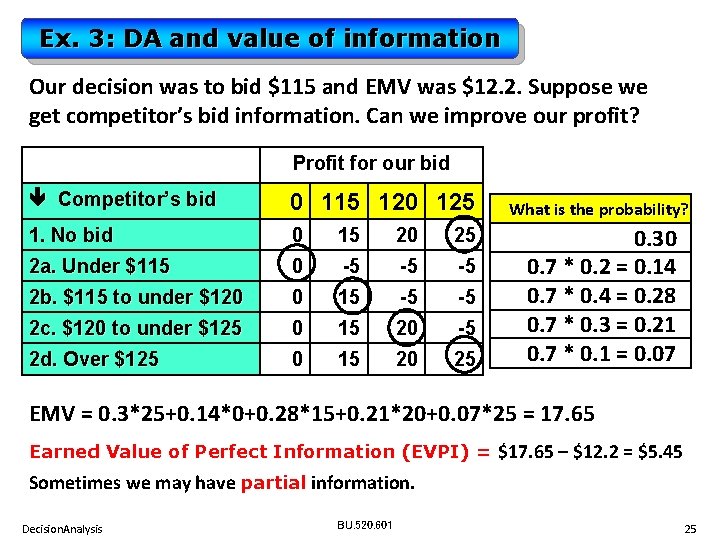
Ex. 3: DA and value of information Our decision was to bid $115 and EMV was $12. 2. Suppose we get competitor’s bid information. Can we improve our profit? Profit for our bid Competitor’s bid 0 115 120 125 1. No bid 0 15 20 25 2 a. Under $115 0 -5 -5 -5 2 b. $115 to under $120 0 15 -5 -5 2 c. $120 to under $125 0 15 20 -5 2 d. Over $125 0 15 20 25 What is the probability? 0. 30 0. 7 * 0. 2 = 0. 14 0. 7 * 0. 4 = 0. 28 0. 7 * 0. 3 = 0. 21 0. 7 * 0. 1 = 0. 07 EMV = 0. 3*25+0. 14*0+0. 28*15+0. 21*20+0. 07*25 = 17. 65 Earned Value of Perfect Information (EVPI) = $17. 65 – $12. 2 = $5. 45 Sometimes we may have partial information. Decision. Analysis BU. 520. 601 25
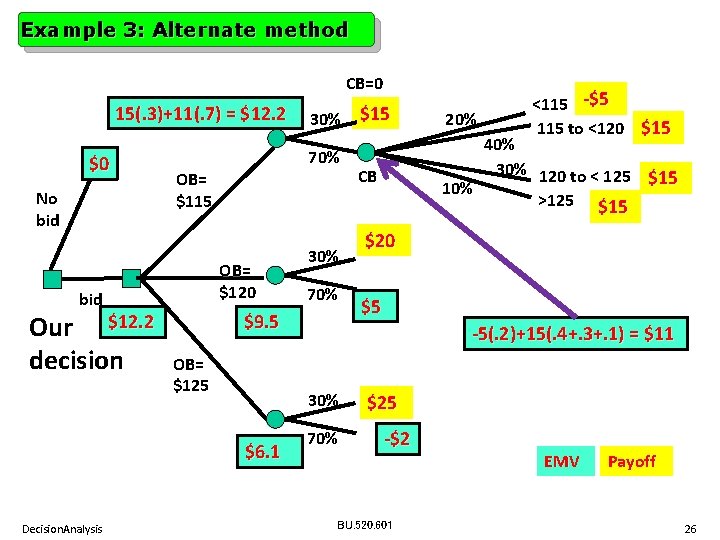
Example 3: Alternate method CB=0 15(. 3)+11(. 7) = $12. 2 $0 No bid Our $12. 2 decision 70% OB= $115 OB= $120 bid 30% 70% $9. 5 OB= $125 20% <115 -$5 115 to <120 $15 40% 30% 120 to < 125 $15 10% >125 $15 CB $20 $5 -5(. 2)+15(. 4+. 3+. 1) = $11 30% $6. 1 Decision. Analysis 30% $15 70% $25 -$2 BU. 520. 601 EMV Payoff 26
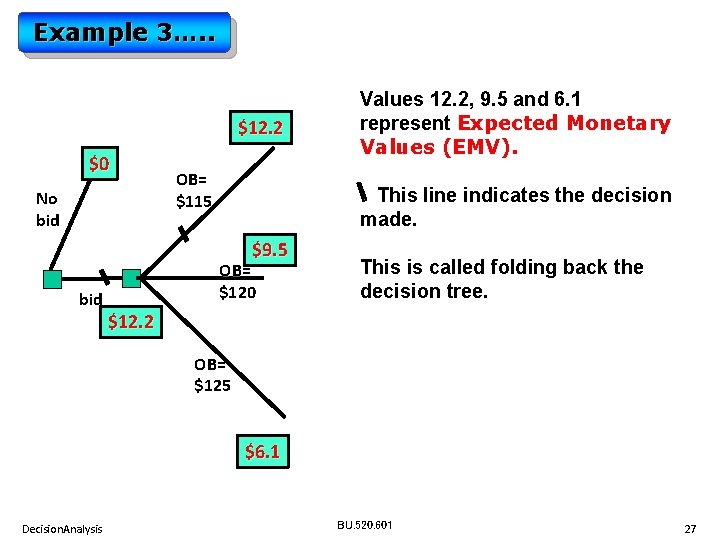
Example 3…. . $12. 2 $0 No bid OB= $115 This line indicates the decision made. $9. 5 bid Values 12. 2, 9. 5 and 6. 1 represent Expected Monetary Values (EMV). OB= $120 This is called folding back the decision tree. $12. 2 OB= $125 $6. 1 Decision. Analysis BU. 520. 601 27

Utility theory Consider the gambling problems again. – Let us flip a fair coin once. – If you win I give you $102 – If I win, you give me $100 – How much will you pay me to play this game: $5, $2, $1, $0 ? Consider another gamble – Let us flip the same coin (500 times) with the same payoffs – How much will you pay me to play this game? Decision. Analysis • • • Different people will pay different amounts to play the first game Expected payoff in the first game is $1 but most people do not want to play the game at all. Why? Losing $100 is a bigger event than winning $102 Most people will play the second game. Still differ in how much they will pay. For most people a gain that is twice as big is not twice as good. A loss of twice as much is more than twice as bad. People’s attitude towards risk can be categorized as: risk averse, risk seeker and risk neutral. A common way to express it is through the decision-maker’s utility function. BU. 520. 601 28
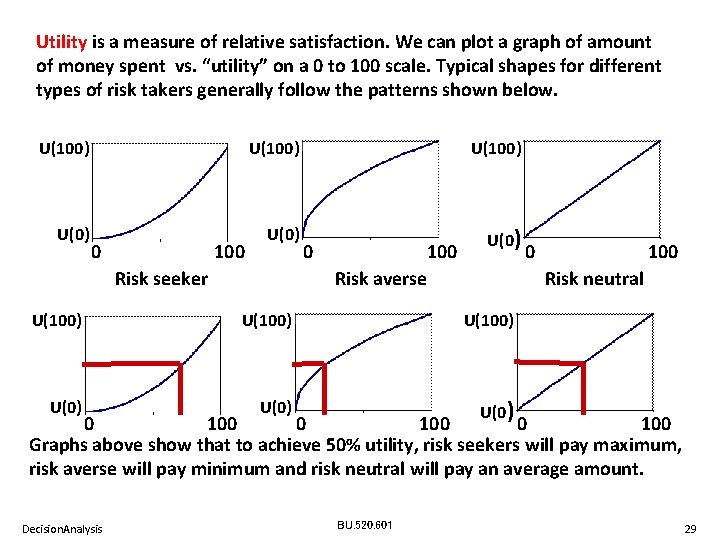
Utility is a measure of relative satisfaction. We can plot a graph of amount of money spent vs. “utility” on a 0 to 100 scale. Typical shapes for different types of risk takers generally follow the patterns shown below. U(100) U(0) 0 100 Risk seeker Risk averse Risk neutral U(100) U(0) 0 100 Graphs above show that to achieve 50% utility, risk seekers will pay maximum, risk averse will pay minimum and risk neutral will pay an average amount. Decision. Analysis BU. 520. 601 29
- Slides: 29