Breaking the ICE Multicollisions in Iterated Concatenated and

Breaking the ICE - Multicollisions in Iterated Concatenated and Expanded (ICE) Hash Functions Ya’akov Hoch and Adi Shamir

Overview n Definitions n Previous results n Our results n Proof of the 3 -permutations case 2

Overview n Definitions n Previous results n Our results n Proof of the 3 -permutations case 3
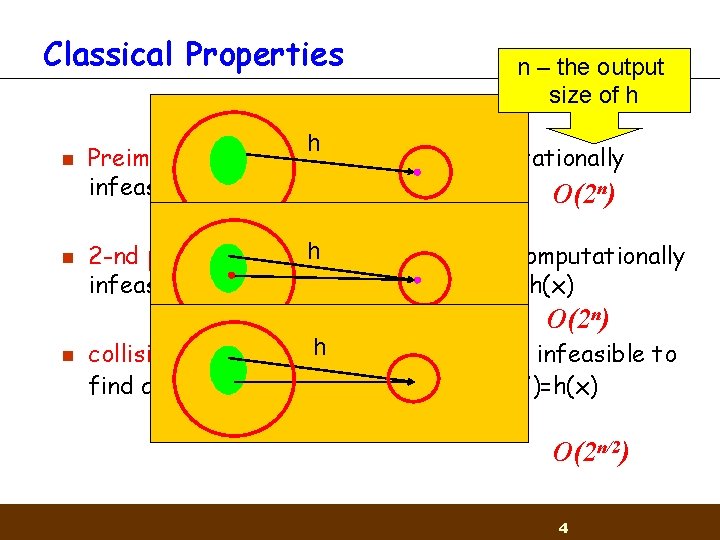
Classical Properties n n n – the output size of h h Preimage resistance: given y it’s computationally infeasible to find a value x s. t. h(x)=y O(2 n) h 2 -nd preimage resistance: given x it’s computationally infeasible to find a value x’ x s. t. h(x’)=h(x) O(2 n) n collision resistance: h it’s computationally infeasible to find any two distinct values x’, x s. t. h(x’)=h(x) O(2 n/2) 4
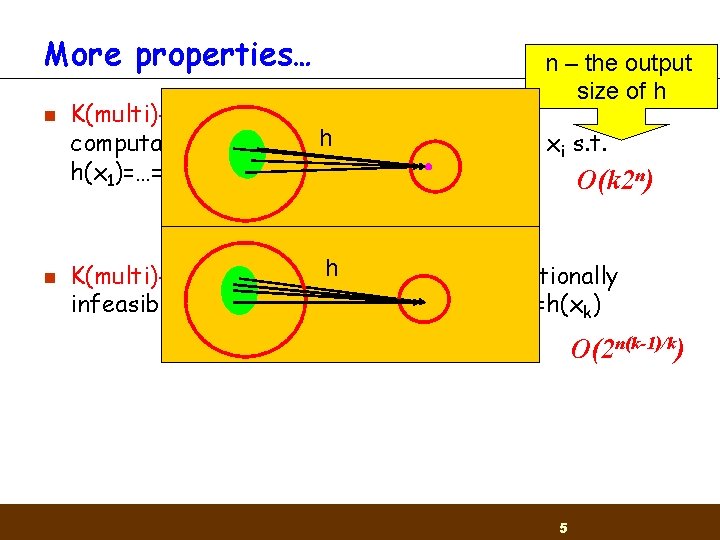
More properties… n n n – the output size of h K(multi)-preimage resistance: given y it’s h to find k values xi s. t. computationally infeasible h(x 1)=…=h(xk)=y O(k 2 n) h K(multi)-collision resistance: it is computationally infeasible to find a k values xi s. t. h(x 1)=…=h(xk) O(2 n(k-1)/k) 5

Iterated Hash Functions n n A standard way to construct hash functions is as follows: Start from an initial hash value h 0 Calculate hi=f(hi-1, mi) f: {0, 1}2 n {0, 1}n Output the last hash value ht m 1 h 0 m 2 h 1 mt h 2 … ht 6

Concatenated Hash Functions n n n Concatenate the outputs of a number of independent hash functions F, G: {0, 1} * {0, 1}n H: {0, 1}* {0, 1) 2 n H(M)=F(M)||G(M) Want to enlarge the output size – to protect against birthday attacks Immunize O(2 n) the construction against discovery of an attack in one of the hash functions Secure against collisions if F and G are random oracles 7

Overview n Definitions n Previous results n Our results n Proof of the 3 -permutations case 8
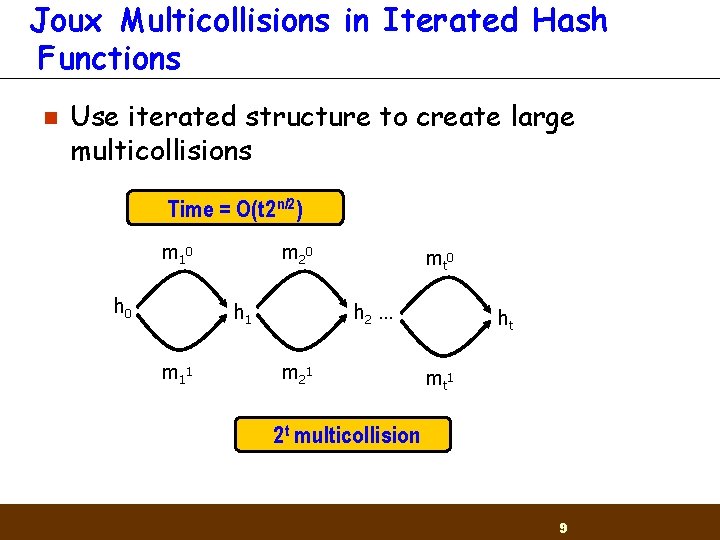
Joux Multicollisions in Iterated Hash Functions n Use iterated structure to create large multicollisions Time = O(t 2 n/2) m 1 0 h 0 m 2 0 h 1 m 1 1 mt 0 h 2 … m 2 1 ht mt 1 2 t multicollision 9

Attacking a concatenated construction n Form a 2 n/2 multicollision in the first hash function We expect to find a collision in the second function among the 2 n/2 colliding messages The attack can be generalized to attack ¨ multiple concatenations ¨ produce multi-preimages (in time 2 n) Mi F(M i) G(M i) M 1 X Y 1 M 2 X Y 2 … … … H(M)=F(M)||G(M) H: {0, 1}* {0, 1}2 n 10

Possible Countermeasures n n Larger internal state - Lucks’ proposition of a double width pipe Expansion - Using message blocks more than once M=m 1 m 2…mt M=m 1 m 2 m 1 m 5 m 1…mtm 2 m 5 mt-1… 11

Problem Statement n n Given a hash function H – find a 2 k multicollision in H Iterated and Concatenated – solved by Joux Iterated, Concatenated and Expanded – a special case solved by Nandi & Stinson Iterated, Concatenated and Expanded (by any constant factor)–solved in this presentation 12
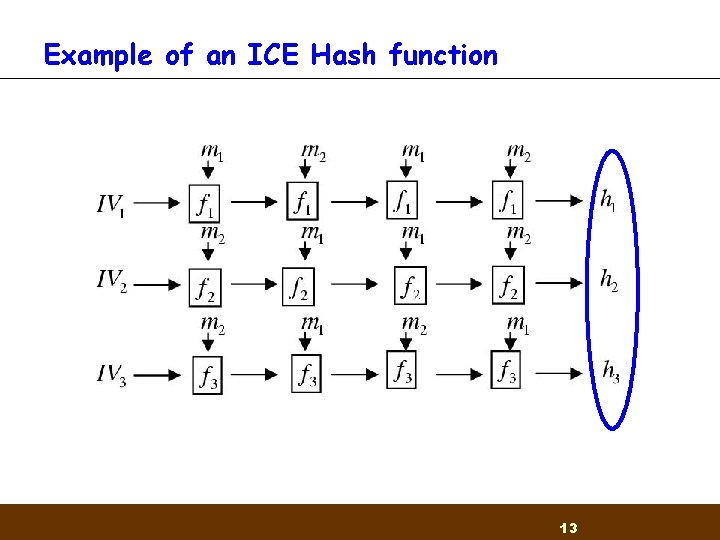
Example of an ICE Hash function 13
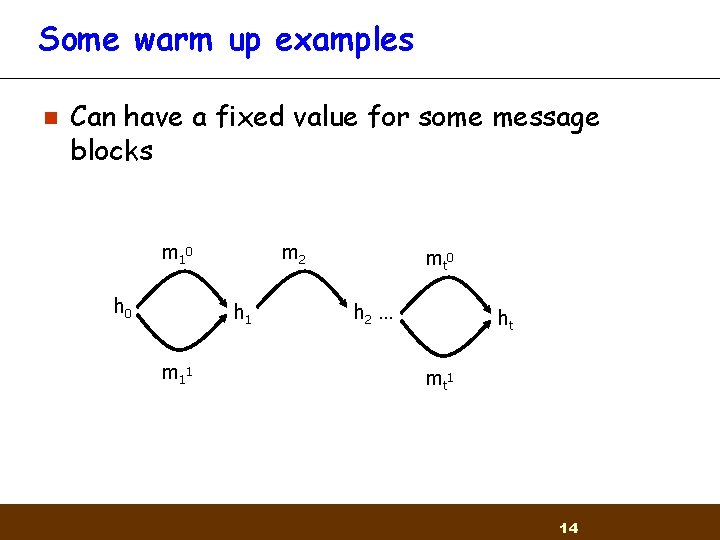
Some warm up examples n Can have a fixed value for some message blocks m 1 0 h 0 m 2 h 1 m 1 1 mt 0 h 2 … ht mt 1 14
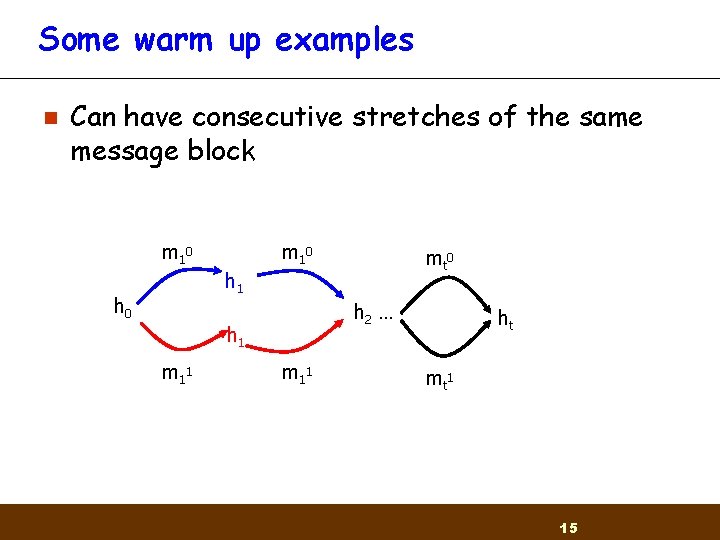
Some warm up examples n Can have consecutive stretches of the same message block m 1 0 mt 0 h 1 h 0 h 2 … h 1 m 1 1 ht mt 1 15
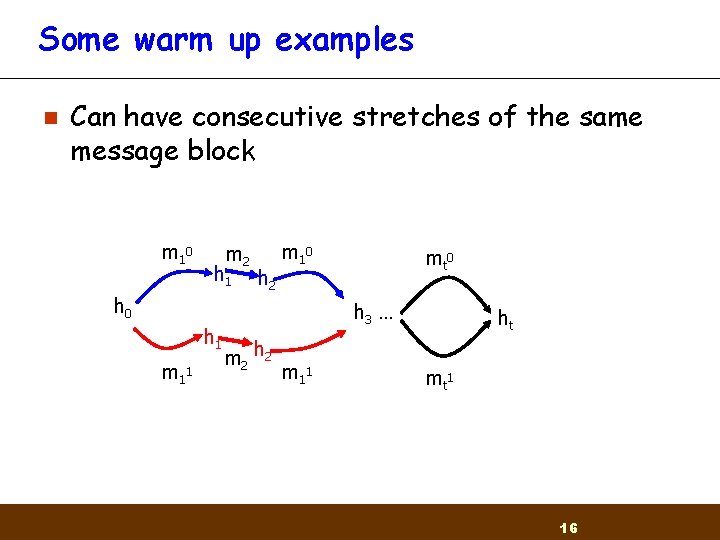
Some warm up examples n Can have consecutive stretches of the same message block m 1 0 m 2 h 1 h 2 m 1 0 h 1 m 1 1 mt 0 h 3 … m 2 h 2 m 1 1 ht mt 1 16

Some warm up examples n n Message expansion takes a message M and outputs M||M Find a 2 k multicollision in the iterated hash function based on the expanded message 17
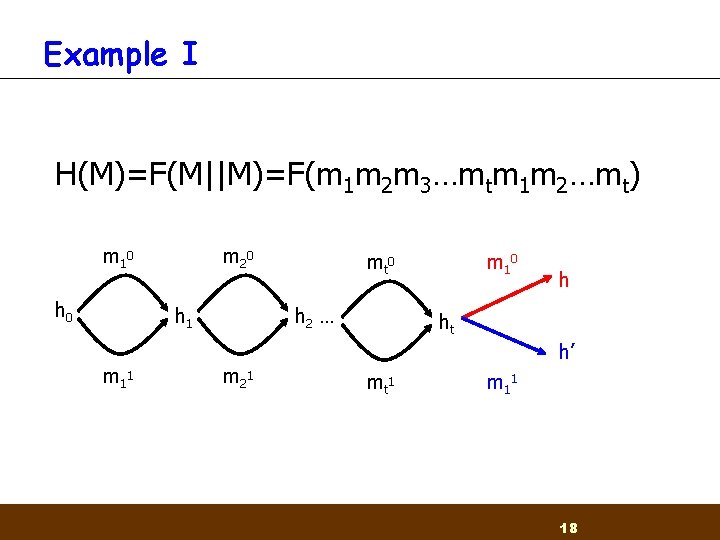
Example I H(M)=F(M||M)=F(m 1 m 2 m 3…mtm 1 m 2…mt) m 1 0 h 0 m 2 0 h 1 m 1 1 mt 0 h 2 … m 2 1 m 1 0 h ht h’ mt 1 m 1 1 18
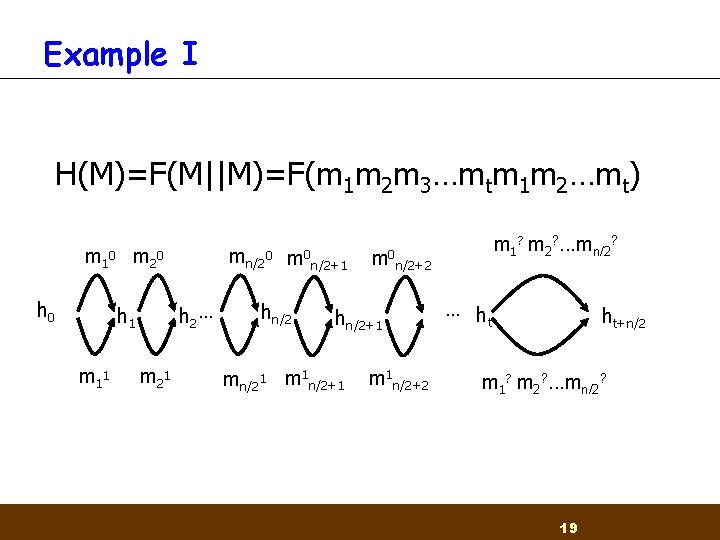
Example I H(M)=F(M||M)=F(m 1 m 2 m 3…mtm 1 m 2…mt) m 1 0 m 2 0 h 2 … h 1 m 1 1 mn/20 m 2 1 m 0 hn/2 n/2+1 m 0 n/2+2 hn/2+1 mn/21 m 1 n/2+1 m 1? m 2? . . . mn/2? m 1 n/2+2 … h t ht+n/2 m 1? m 2? . . . mn/2? 19

Example I H(M)=F(M||M)=F(m 1 m 2 m 3…mtm 1 m 2…mt) m 1 0 m 2 0 h 2 … h 1 m 1 1 mn/20 m 2 1 m 0 hn/2 n/2+1 m 0 n/2+2 hn/2+1 mn/21 m 1 n/2+1 m 1? m 2? . . . mn/2? m 1 n/2+2 … h t ht+n/2 m 1? m 2? . . . mn/2? 20

Example I H(M)=F(M||M)=F(m 1 m 2 m 3…mtm 1 m 2…mt) m 1 0 m 2 0 h 0 m 1 1 mn/20 …h t h 2 … h 1 m 2 1 m 1? m 2? . . . mn/2? mn/21 ht+n/2… h 2 t m 1? m 2? . . . mn/2? Works for any fixed of repetitions 22 t/nnumber multicollision 21

Example II - 2 successive permutations n n n Message expansion adds a permutation of the original message blocks E(M) = m 1 m 2…mtm (1)m (2)…m (t) Use the same procedure as before m 1 0 m 2 0 h 0 …h t h 2 … h 1 m 1 1 mn/20 m 2 1 mn/21 m (1)? . . . m (n/2)? ht+n/2… h 2 t m (1)? . . . m (n/2)? 22

Previous results (Nandi & Stinson) n If the message expansion contains each message block at most twice, can find a 2 k multicollision in time 2 n/2 C(n, k) where C(n, k) is polynomial in n, k 23

Overview n Definitions n Previous results n Our results n Proof of the 3 -permutations case 24

Our results n If the message expansion expands by a constant factor e (by duplicating message blocks) can find a 2 k multicollision in time 2 n/2 C(n, k, e) where C(n, k, e) is polynomial in n, k (but exponential in e) 25
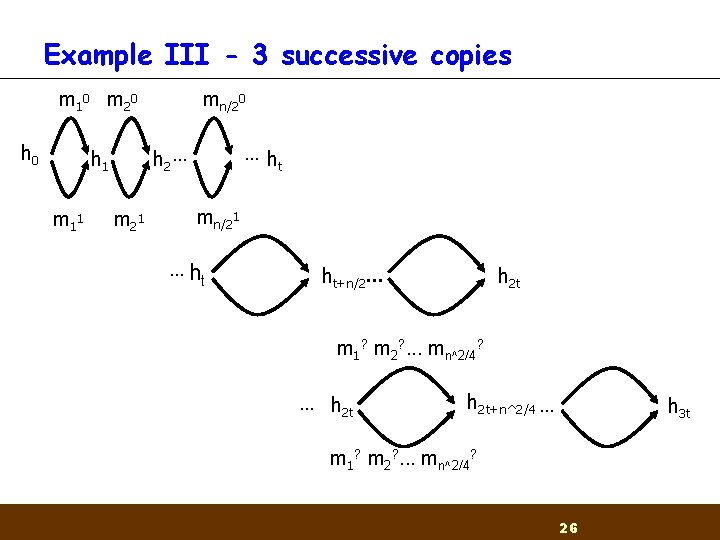
Example III - 3 successive copies m 1 0 m 2 0 h 0 …h t h 2 … h 1 m 1 1 mn/20 m 2 1 mn/21 … ht ht+n/2… h 2 t m 1? m 2? . . . mn^2/4? … h 2 t+n^2/4 … h 3 t m 1? m 2? . . . mn^2/4? 26
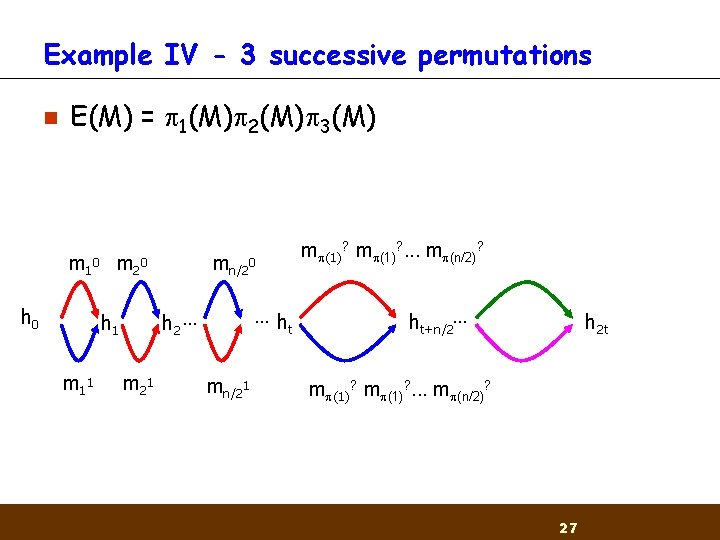
Example IV - 3 successive permutations n E(M) = 1(M) 2(M) 3(M) m 1 0 m 2 0 h 0 …h t h 2 … h 1 m 1 1 mn/20 m 2 1 mn/21 m (1)? . . . m (n/2)? ht+n/2… h 2 t m (1)? . . . m (n/2)? 27
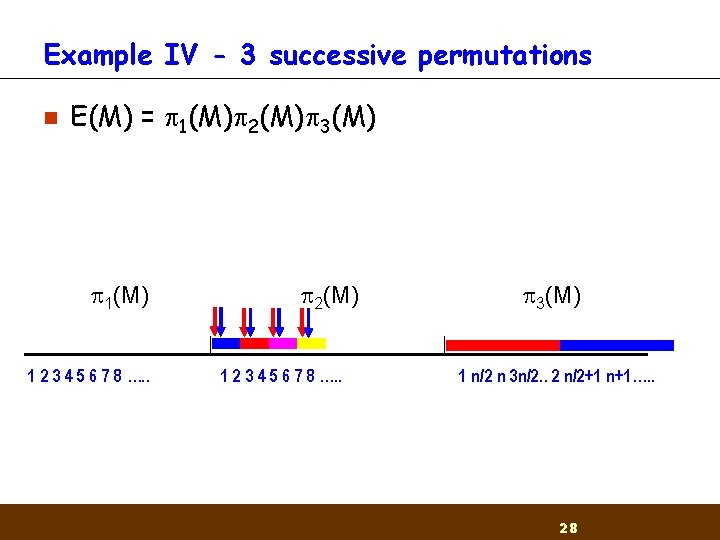
Example IV - 3 successive permutations n E(M) = 1(M) 2(M) 3(M) 1(M) 1 2 3 4 5 6 7 8 …. . 2(M) 1 2 3 4 5 6 7 8 …. . 3(M) 1 n/2 n 3 n/2. . 2 n/2+1 n+1…. . 28

Overview n Definitions n Previous results n Our results n Proof of the 3 -permutations case 29
![Getting started Lemma 1: Let B and C be two permuted sequences of [L]. Getting started Lemma 1: Let B and C be two permuted sequences of [L].](http://slidetodoc.com/presentation_image_h/3800ddebb0ac044e6a4ce91cd1491a86/image-30.jpg)
Getting started Lemma 1: Let B and C be two permuted sequences of [L]. Divide B into k consecutive groups B 1, . . . , Bk and C into C 1, . . . , Ck of size n/k. Then for x>0 and L¸ k 3 x there exists a perfect matching of Bi's and Cj's such that |Bi Cj | ¸ x n 30
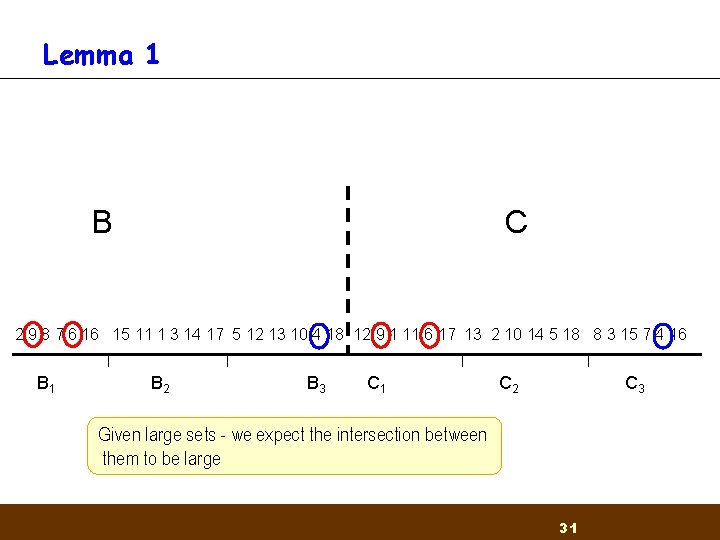
Lemma 1 B C 2 9 8 7 6 16 15 11 1 3 14 17 5 12 13 10 4 18 12 9 1 11 6 17 13 2 10 14 5 18 8 3 15 7 4 16 B 1 B 2 B 3 C 1 C 2 C 3 Given large sets - we expect the intersection between them to be large 31
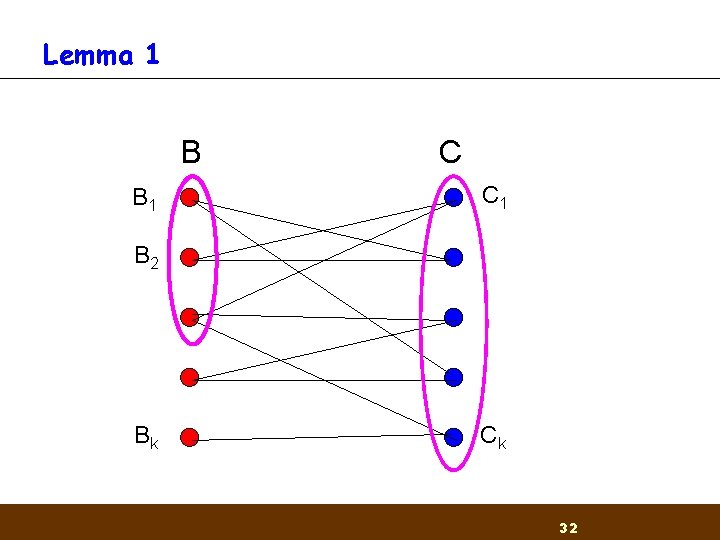
Lemma 1 B B 1 C C 1 B 2 Bk Ck 32
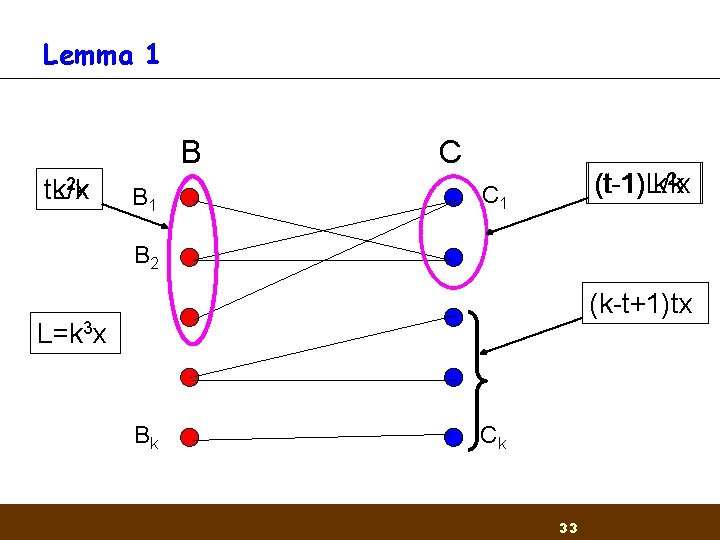
Lemma 1 B 2 x t. L/k tk B 1 C (t-1)L/k (t-1) k 2 x C 1 B 2 (k-t+1)tx L=k 3 x Bk Ck 33
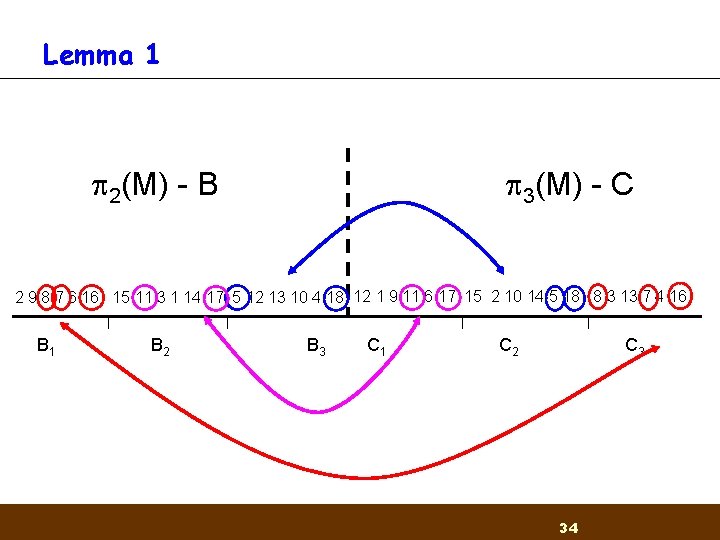
Lemma 1 2(M) - B 3(M) - C 2 9 8 7 6 16 15 11 3 1 14 17 5 12 13 10 4 18 12 1 9 11 6 17 15 2 10 14 5 18 8 3 13 7 4 16 B 1 B 2 B 3 C 1 C 2 C 3 34

3 consecutive permutations n n Find a matching for x=n 2/4 in the last two permutations Set all non active message blocks to 0 Build the multi-collision in 3 stages using larger blocks in each stage Requires a message of length O(k 3 n 2) 35

3 successive permutations 36

Many successive permutations n E(M) = 1(M) 2(M)… q(M) . . . q-1(M) q(M) 37

q consecutive permutations n n n Find a matching for x=O(n 3(q-3)+2) in the last two permutations Set all non active message blocks to 0 Find a matching for x=O(n 3(q-6)+2) in the two second to last permutations … Build the multi-collision in q stages using larger blocks in each stage Requires a message of length O(k 3 n 3(q-3)+2) 38

Reduction from the general case n n So far proved for any constant number of permutations Reduction from general case to succesive permutations: ¨ Choose a set of active message indices such that the resulting sequence is in successive permutations form 39

Case of expansion factor 2 n n At least half the indices appear at most twice Given a sequence in which each index appears at most twice either ¨ There exists a subset of variables which ‘appears’ once ¨ There exists a subset of variables which are in successive permutation form 40

Case of expansion factor 2 n Lemma: for any 2 -sequence over 1. . l where l=MN either ¨ There exists a subset of M variables which ‘appears’ once ¨ There exists a subset of N variables which are in successive permutation form 41

Case of expansion factor 2 Case 2 : 1 N: M-1 elements appear in concatenated Case elements appear only once permutation form n Proof: by induction on l=MN (M-1)N 1 7 4 9 8 3 76 5 4 2 9 13… N 7 does not appear now! If each element appears at most once we are done!! 42

General Case n n At least half the indices appear at most twice the expansion rate e Given a sequence in which each index appears at most 2 e either ¨ There exists a subset of variables which ‘appears’ once ¨ There exists a subset of variables which are in successive permutation form n We already solved the successive permutation case 43

General Case n If the message expansion expands by a constant factor e (by duplicating message blocks) can find a 2 k multicollision in time 2 n/2 C(n, k, e) where C(n, k, e) is polynomial in n, k but exponential in e) 44
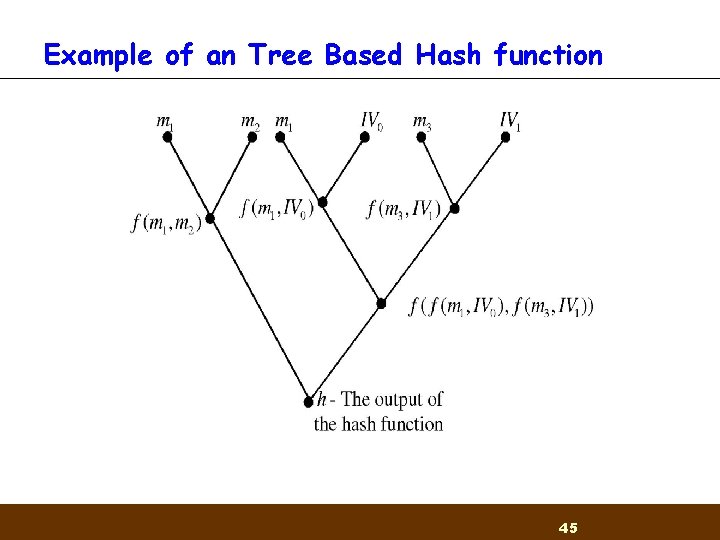
Example of an Tree Based Hash function 45

Further research n Other message expansion procedures ¨ Linear combinations ¨ LFSRs ¨… n n n Keyed hash functions Tree based hash functions Other uses of multicollisions 46
- Slides: 46