Brand Management 2 x 2 model As part

Brand Management 2 x 2 model As part of a brand management experiment, several types of cereal packages were designed. Two colors and two styles of lettering were considered. Each combination was used to produce a package, and each of these combinations was test marketed in 6 comparable stores. At the end of the evaluation period, sales in the 24 (6 x 4) stores were compared.

The data • Y = Sales per store (number of packages); • x 1 = Color of the box: § Green (0) or Red (1); – x 2 = Lettering Style : § Classic (0) o Modern (1). RQ: What is the right combination of color and type style, or does it matter? Data: http: //www. cs. unitn. it/~taufer/Data/Design. txt

Notes • IV are qualitative: there are 4 groups which we want to compare. • A model with interaction allow for all possible combinations of Style and Color E(Y) = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 1 x 2 • The estimated β coefficents will be the mean differences in sales for the 4 groups in the sample • The testing machinery available for regression can be used for probabilistic comparison of groups

Model: E(Y) = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 1 x 2 If x 1 = 0 and x 2 = 0, green-classic (GC) is the reference group E(Y) = β 0 = μGC expected sales for GC If x 1 = 0 and x 2 = 1, green-modern (GM) E(Y) = β 0 + β 2 = μGM expected sales for GM β 2 = μVM - μVC expected difference between GC and GM

Model: E(Y) = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 1 x 2 If x 1 = 1 and x 2 = 0, red-classic (RC) E(Y) = β 0 + β 1 = μRC , β 1 = μRC – μGC expected difference for classic style when passing from green to red If x 1 = 1 and x 2 = 1, red-modern (RM) E(Y) = β 0 + β 1 + β 2 + β 3 = μRM β 3 = (μRM – μRC ) – (μGM – μGC) interaction: difference of differences C-M for red and C-M for green.
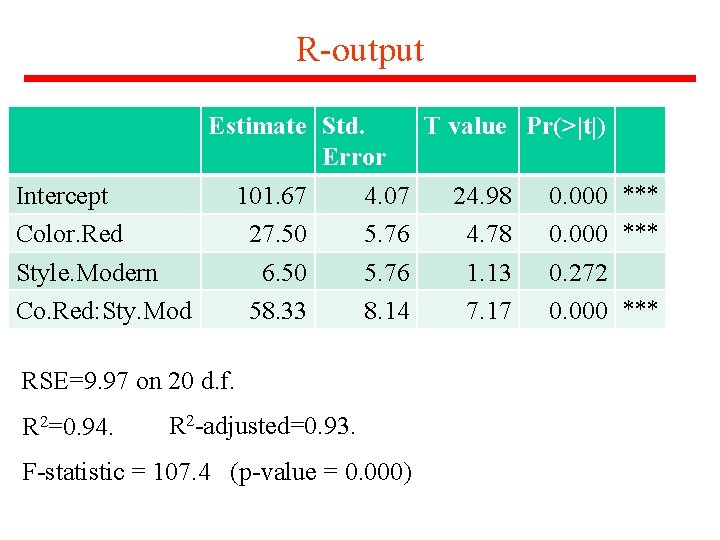
R-output Estimate Std. T value Pr(>|t|) Error Intercept 101. 67 4. 07 24. 98 0. 000 *** Color. Red 27. 50 5. 76 4. 78 0. 000 *** Style. Modern 6. 50 5. 76 1. 13 0. 272 Co. Red: Sty. Mod 58. 33 8. 14 7. 17 0. 000 *** RSE=9. 97 on 20 d. f. R 2=0. 94. R 2 -adjusted=0. 93. F-statistic = 107. 4 (p-value = 0. 000)
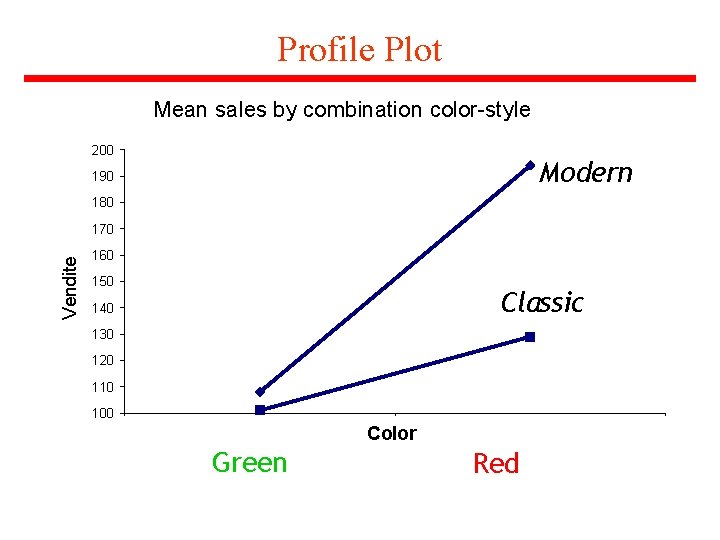
Profile Plot Mean sales by combination color-style 200 Modern 190 180 Vendite 170 160 150 Classic 140 130 120 110 100 Color Green Red

Color effect Hypotheses of interest H 0: β 1 = β 3 = 0 color does not affect sales F-Statistic = 122. 65; p-value = 0. 000, REJECT H 0. Lettering Effect H 0: β 2 = β 3 = 0 lettering does not affect sales F-Statistic = 64. 101; p-value = 0. 000, REJECT H 0. Interaction H 0: β 3 = 0 no moderating (sinergy) effect F-Statistic = 51. 37; p-value = 0. 000, REJECT H 0.
- Slides: 8