Boyer Moore Algorithm Idan Szpektor Boyer and Moore

Boyer Moore Algorithm Idan Szpektor

Boyer and Moore

What It’s About n A String Matching Algorithm n Preprocess a Pattern P (|P| = n) n For a text T (| T| = m), find all of the occurrences of P in T n Time complexity: O(n + m), but usually sub- linear

Right to Left (like in Hebrew) n Matching the pattern from right to left n For a pattern abc: T: P: ↓ bbacdcbaabcddcdaddaaabcbcb abc n Worst case is still O(n m)

The Bad Character Rule (BCR) n On a mismatch between the pattern and the text, we can shift the pattern by more than one place. Sublinearity! ddbbacdcbaabcddcdaddaaabcbcb acabc ↑
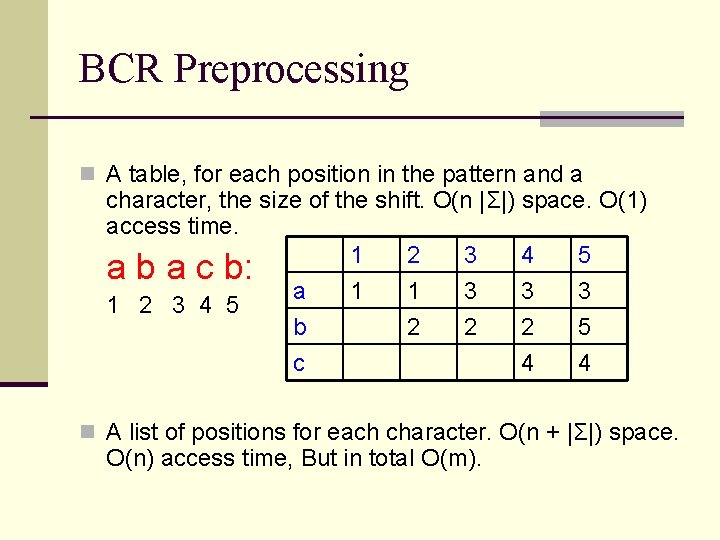
BCR Preprocessing n A table, for each position in the pattern and a character, the size of the shift. O(n |Σ|) space. O(1) access time. 1 2 3 4 5 a b a c b: a 1 1 3 3 3 1 2 3 4 5 b 2 2 2 5 c 4 4 n A list of positions for each character. O(n + |Σ|) space. O(n) access time, But in total O(m).

BCR - Summary n On a mismatch, shift the pattern to the right until the first occurrence of the mismatched char in P. n Still O(n m) worst case running time: T: aaaaaaaaaaaaa P: abaaaa

The Good Suffix Rule (GSR) n We want to use the knowledge of the matched characters in the pattern’s suffix. n If we matched S characters in T, what is (if exists) the smallest shift in P that will align a sub-string of P of the same S characters ?

GSR (Cont…) n Example 1 – how much to move: ↓ T: bbacdcbaabcddcdaddaaabcbcb P: cabbabdbab

GSR (Cont…) n Example 2 – what if there is no alignment: ↓ T: bbacdcbaabcbbabdbabcaabcbcb P: bcbbabdbabc

GSR - Detailed n We mark the matched sub-string in T with t and the mismatched char with x 1. In case of a mismatch: shift right until the first occurrence of t in P such that the next char y in P holds y≠x 2. Otherwise, shift right to the largest prefix of P that aligns with a suffix of t.

Boyer Moore Algorithm n Preprocess(P) n k : = n while (k ≤ m) do n Match P and T from right to left starting at k n If a mismatch occurs: shift P right (advance k) by max(good suffix rule, bad char rule). n else, print the occurrence and shift P right (advance k) by the good suffix rule.

Algorithm Correctness n The bad character rule shift never misses a match n The good suffix rule shift never misses a match

Preprocessing the GSR – L(i) n L(i) – The biggest index j, such that j < n and prefix P[1. . j] contains suffix P[i. . n] as a suffix but not suffix P[i-1. . n] 1 2 3 4 5 6 7 8 9 10 11 12 13 P: b b a a b b c a b b L: 0 0 0 0 0 5 9 0 12

Preprocessing the GSR – l(i) n l(i) – The length of the longest suffix of P[i. . n] that is also a prefix of P P: b b a a b b c a b b l: 2 2 2 1

Using L(i) and l(i) in GSR n If mismatch occurs at position n, shift P by 1 n If a mismatch occurs at position i-1 in P: n If L(i) > 0, shift P by n – L(i) n else shift P by n – l(i) n If P was found, shift P by n – l(2)
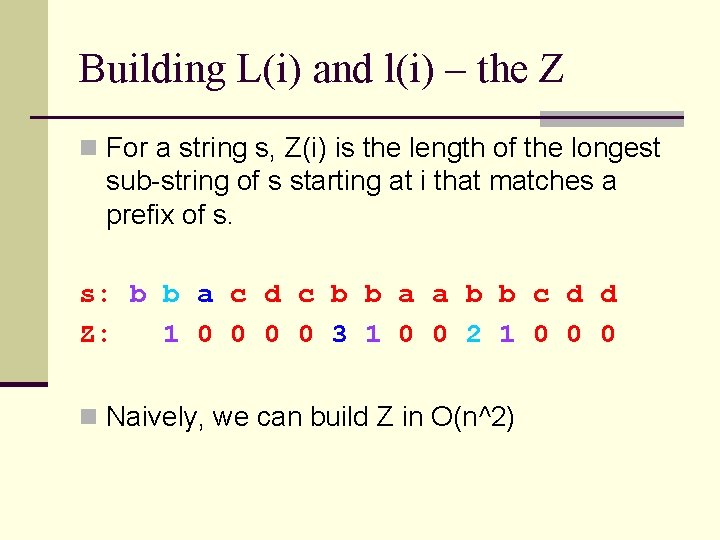
Building L(i) and l(i) – the Z n For a string s, Z(i) is the length of the longest sub-string of s starting at i that matches a prefix of s. s: b b a c d c b b a a b b c d d Z: 1 0 0 3 1 0 0 2 1 0 0 0 n Naively, we can build Z in O(n^2)
![From Z to N n N(i) is the longest suffix of P[1. . i] From Z to N n N(i) is the longest suffix of P[1. . i]](http://slidetodoc.com/presentation_image_h2/3fb46f5d5f45d066c53b64aa317e0339/image-18.jpg)
From Z to N n N(i) is the longest suffix of P[1. . i] that is also a suffix of P. n N(i) is Z(i), built over P reversed. s: d d c b b a a b b c d c a b b N: 0 0 0 1 2 0 0 1 3 0 0 1

Building L(i) in O(n) n L(i) – The biggest index j < n, such that prefix P[1. . j] contains suffix P[i. . n] as a suffix but not suffix P[i-1. . n] n L(i) – The biggest index j < n such that: N(j) == | P[i. . n] | == n – i + 1 n for i : = 1 to n, L(i) : = 0 n for j : = 1 to n-1 n n i : = n – N(j) + 1 L(i) : = j

Building l(i) in O(n) n l(i) – The length of the longest suffix of P[i. . n] that is also a prefix of P n l(i) – The biggest j <= | P[i. . n] | == n – i + 1 such that N(j) == j n k : = 0 n for j : = 1 to n-1 n n If(N(j) == j), k : = j l(n – j + 1) : = k

Building Z in O(n) n For calculating Z(i), we want to use the previously calculated Z(1)…Z(i-1) n For each I we remember the right most Z(j): j, such that j < i and j + Z(j) >= k + Z(k), for all k<i
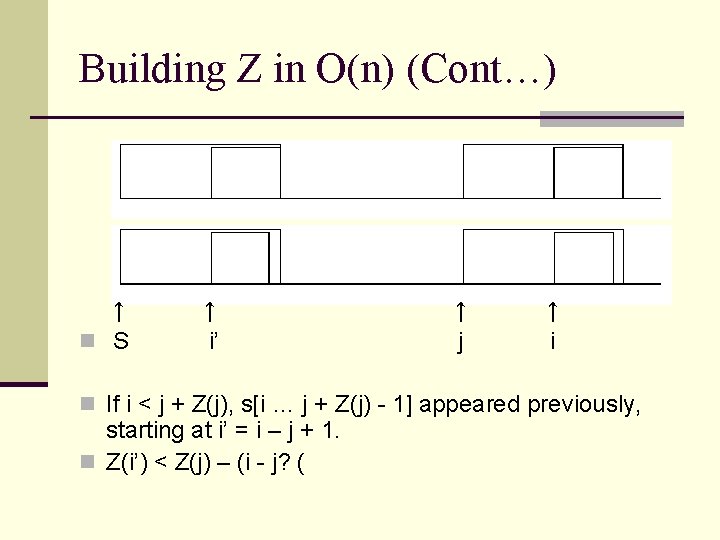
Building Z in O(n) (Cont…) ↑ n S ↑ i’ ↑ j ↑ i n If i < j + Z(j), s[i … j + Z(j) - 1] appeared previously, starting at i’ = i – j + 1. n Z(i’) < Z(j) – (i - j? (

Building Z in O(n) (Cont…) n For Z(2) calculate explicitly n j : = 2, i : = 3 n While i <= |s|: if i >= j + Z(j), calculate Z(i) explicitly n else n Z(i) : = Z(i’) n If Z(i’) >= Z(j) – (i - j), calculate Z(i) tail explicitly n If j + Z(j) < i + Z(i), j : = i n

Building Z in O(n) - Analysis n The algorithm builds Z correctly n The algorithm executes in O(n) n A new character is matched only once n All other operations are in O(1)

Boyer Moore Worst Case Analysis n Assume P consists of n copies of a single char and T consists of m copies of the same char: T: aaaaaaaaaaaaa P: aaaaaa n Boyer Moore Algorithm runs in Θ(m n) when finding all the matches

The Galil Rule n In a specific matching phase, We mark with k the position in T of the right end of P. We mark with s the position of last matched char in this phase. s k k’ T: bbacdcbaabcddcdaddaaabcbcb P: abaab

The Galil Rule (Cont…) n All the chars in position s < j ≤ k are known to be matching. The algorithm doesn’t need to check them. n An extended Boyer Moore algorithm with the Galil rule runs in O(m + n) worst case (even without the bad-character rule).

Don’t Sleep Yet…

O(n + m) proof - Outline n Preprocess in O(n) – already proved 1. Properties of strings 2. Proof of search in O(m) if P is not in T, using only the good suffix rule. 3. Proof of search in O(m) even if P is in T, adding the Galil rule.

Properties of Strings n If for two strings δ, γ: δγ = γδ then there is a string β such that δ = βi and γ = βj, i, j > 0 - Proof by induction n Definition: A string s is semiperiodic with period β if s consists of a non-empty suffix of β (possibly the entire β) followed by one or more complete copies of β. β’ β β β

Properties of Strings (Cont…) n A string is prefix semiperiodic if it contains one or more complete copies of β followed by a non-empty prefix of β. n A string is prefix semiperiodic iff it is semiperiodic with the same length period

Lemma 1 n Suppose P occurs in T starting at position p and also at position q, q > p. If q – p ≤ n/2 then P is semiperiodic with period α = P[n-(q-p)+1…n] p α’ α α α α q α

Proof - when P is Not Found in T n We have R rounds during the search. n After each round the good suffix rule decides on a right shift of si chars. n Σsi ≤ m n We shall use Σsi as an upper bound.

Proof (Cont…) n For each round we count the matched chars by: n fi – the number of chars matched for the first time n gi –the number of chars already matched in previous rounds. n Σfi = m n We want to prove that gi ≤ 3 si ( Σgi ≤ 3 m).

Proof (Cont…) n Each round don’t find P it matched a substring ti and one bad char xi in T (xiti T) T: bbacdcbaabcbbabdbabcaabcbcb P: bdbabc n |ti|+1 ≤ 3 si gi ≤ 3 si (because gi + fi = |ti|+1) n For the rest of the proof we assume that for the specific round i: |ti| + 1 > 3 si

Lemma 2 (|ti| + 1 > 3 si) n In round i we look at the matched suffix of P, marked P*. P* = yi ti, yi≠ xi. n Both P* and ti are semiperiodic with period α of length si and hence with minimal length period β, α = βk. n Proof: by Lemma 1.

Lemma 3 (|ti| + 1 > 3 si) n Suppose P overlapped ti during round i. We shall examine in what ways could P overlap ti in previous rounds. n In any round h < i, the right end of P could not have been aligned with the right end of any full copy of β in ti. - proof: n Both round h and i fail at char xi n two cases of possible shift after round h are invalid

Lemma 4 (|ti| + 1 > 3 si) n In round h < i, P can correctly match at most |β|-1 chars in ti. n By Lemma 3, P is not aligned with a right end of ti in phase h. n Thus if it matched |β| chars or more there is a suffix γ of β followed by a prefix δ of β such that δ γ = γ δ. n By the string properties there is a substring μ such that β = μk, k>1. n This contradicts the minimal period size property of β.

Lemma 5 (|ti| + 1 > 3 si) n If in round h < i the right end of P is aligned with a char in ti, it can only be aligned with one of the following: n One of the left-most |β|-1 chars of ti n One of the right-most |β| chars of ti -proof: n n If not, By Lemma 3, 4, max |β|-1 chars are matched and only from the middle of a β copy, while there at least |β| A shift cannot pass the right end of that β copy

Proof (Cont…) n If |ti| + 1 > 3 si then gi ≤ 3 si n Using Lemma 5, in previous rounds we could match only the bad char xi, the last |β|-1 chars in ti or start from the first |β| right chars in ti. n In the last case, using Lemma 4, we can only match up to |β|-1 chars n in total we could previously match: gi = 1 + |β|-1 + (|β| + |β|-1) ≤ 3|β| ≤ 3 si

Proof - Final n Number of matches = ∑(fi + gi) = ∑fi + ∑gi ≤ m + ∑ 3 si ≤ m + 3 m = 4 m

Proof - when P is Found in T n Split the rounds to two groups: n “match” rounds –an occurrence of P in T was found. n “mismatch” rounds –P was not found in T. n we have proved O(m) for “mismatch” rounds.

Proof (Cont…) n After P was found in T, P will be shifted by a constant length s. (s = n – l(2)). n |n| + 1 ≤ 3 s ∑ matches in round i ≤ ∑ 3 s ≤ m n For the rest of the proof we assume that: |n| + 1 > 3 s

Proof (|n| + 1 > 3 s) n By Lemma 1, P is semiperiodic with minimal length period β, |β| = s. n If round i+1 is also a “match” round then, by the Galil rule, only the new |β| chars are compared. n A contiguous series of “match” rounds, i…i+k is called a “run”.

Proof (|n| + 1 > 3 s) n ∑ The length of a “run”, not including chars that where already matched in previous “runs” ≤ m n How many chars in a “run” where already matched in previous “runs”?

Lemma (|n| + 1 > 3 s) n Suppose k-1 was a “match” round and k is a “mismatch” round that ends the “run”. n If k’ > k is the first “match” round then it overlaps at most |β|-1 chars with the previous “run” (ended by round k-1). n The left end of P at round k’ cannot be aligned with the left end of a full copy of |β| at round k-1. n As a result, P cannot overlap |β| chars or more with round k-1.

Proof (|n| + 1 > 3 s) n By the Lemma and because the shift after every “match” round is of |β|, only the first round of a “run” can overlap, and only with the last previous “run”. n ∑ The length of the chars that where already matched in previous “runs” ≤ m

Proof (|n| + 1 > 3 s) - Final n ∑ The length of a “run” = ∑ The length of a “run”, not including chars that where already matched in previous “runs” + ∑ The length of the chars that where already matched in previous “runs” ≤ m+m
- Slides: 48