Boxplots Box and Whisker Plots Boxplots constructed based
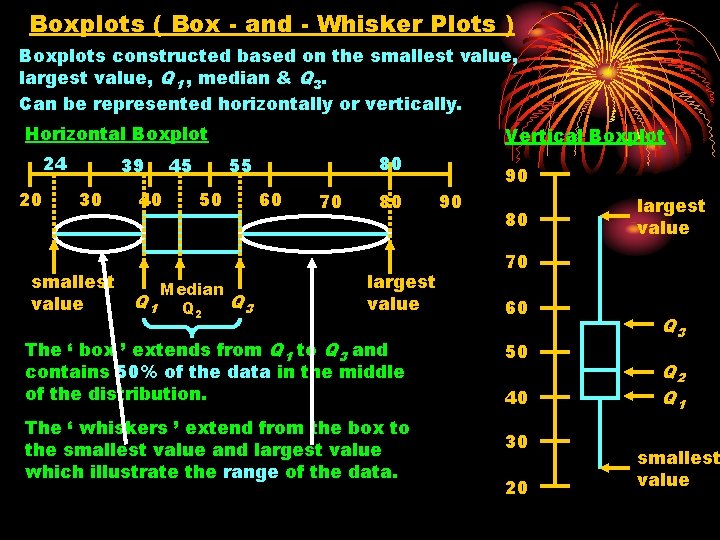
Boxplots ( Box - and - Whisker Plots ) Boxplots constructed based on the smallest value, largest value, Q 1 , median & Q 3. Can be represented horizontally or vertically. Horizontal Boxplot 24 20 39 30 smallest value 40 45 Vertical Boxplot 80 55 50 Median Q 1 Q 2 Q 3 60 70 80 largest value The ‘ box ’ extends from Q 1 to Q 3 and contains 50% of the data in the middle of the distribution. The ‘ whiskers ’ extend from the box to the smallest value and largest value which illustrate the range of the data. 90 90 80 largest value 70 60 50 40 30 20 Q 3 Q 2 Q 1 smallest value
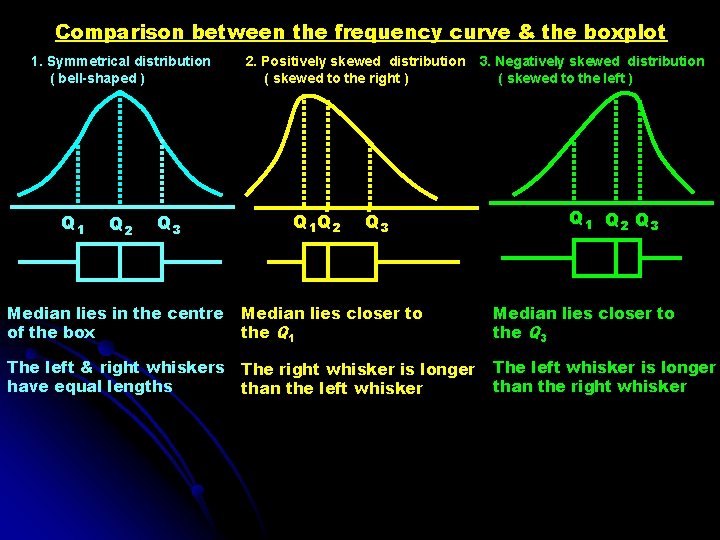
Comparison between the frequency curve & the boxplot 1. Symmetrical distribution ( bell-shaped ) Q 1 Q 2 Q 3 2. Positively skewed distribution ( skewed to the right ) Q 1 Q 2 Q 3 3. Negatively skewed distribution ( skewed to the left ) Q 1 Q 2 Q 3 Median lies in the centre of the box Median lies closer to the Q 1 Median lies closer to the Q 3 The left & right whiskers have equal lengths The right whisker is longer than the left whisker The left whisker is longer than the right whisker

Example 1 : The stemplot below shows the number of flies caught in an insect trap for 28 days Stem Leaf Solution : 0 1 1 2 3 5 5 5 6 2 2 2 3 5 8 8 3 4 4 5 7 7 9 4 2 6 7 7 8 Smallest value = 1 Largest value = 48 Q 1 = x 7 + x 8 2 Q 2 = x 14+ x 15 2 Key : 1 | 2 means 12 flies = 15 + 15 2 = 15 = 28 + 28 = 28 2 a) Illustrate the data by drawing a boxplot Q 3 = x 21+ x 22 = 37 + 37 = 37 2 2 b) Use your boxplot to comment on the type of distribution. a) 0 10 1 20 30 40 50 48 15 28 37 b) The median is closer to the Q 3 and the left whisker is longer than the right whisker. Therefore, the distribution is skewed to the left or negatively skewed.

Example 2 : The following data shows a summary of the marks for Mathematics & Biology for students. Subjects Minimum Maximum Median Q 1 Q 3 Mathematics 10 90 60 45 70 Biology 35 85 60 48 72 Draw two boxplots for this data & give comments regarding the distribution of marks for Mathematics & Biology. Solution : 10 20 30 40 50 60 70 80 90 Mathematics Biology Exercise 5. 12 pg. 222 Comment : Q. 1, 2, 3, 4, 5 & 7 The median for both subjects are the same but the marks for Mathematics shows a bigger range & it is skewed to the left. The Biology marks has a smaller range compared to Mathematics & it has symmetrical distribution.
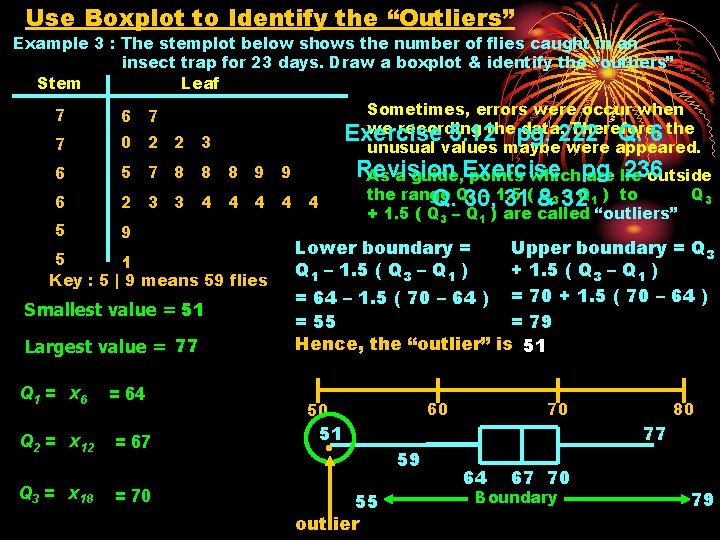
Use Boxplot to Identify the “Outliers” Example 3 : The stemplot below shows the number of flies caught in an insect trap for 23 days. Draw a boxplot & identify the “outliers” Stem Leaf Sometimes, errors were occur when we recording data. 222 Therefore, Exercise 5. 12 thepg. Q. 6 the unusual values maybe were appeared. 7 6 7 7 0 2 2 3 6 5 7 8 8 8 9 9 6 2 3 3 4 4 4 5 9 5 1 Key : 5 | 9 means 59 flies Smallest value = 51 Largest value = 77 Q 1 = x 6 Q 2 = x 12 Q 3 = x 18 = 64 = 67 = 70 Revision 236 As a guide, Exercise points whichpg. are lie outside the range Q 3 32 – Q 1 ) to Q 3 1 – 1. 5 Q. Q 30, 31( & + 1. 5 ( Q 3 – Q 1 ) are called “outliers” Lower boundary = Q 1 – 1. 5 ( Q 3 – Q 1 ) Upper boundary = Q 3 + 1. 5 ( Q 3 – Q 1 ) = 64 – 1. 5 ( 70 – 64 ) = 70 + 1. 5 ( 70 – 64 ) = 55 = 79 Hence, the “outlier” is 51 60 50 51 55 outlier 59 70 80 77 64 67 70 Boundary 79
- Slides: 5