Boundary Representations and Topology Dr Scott Schaefer 1

Boundary Representations and Topology Dr. Scott Schaefer 1

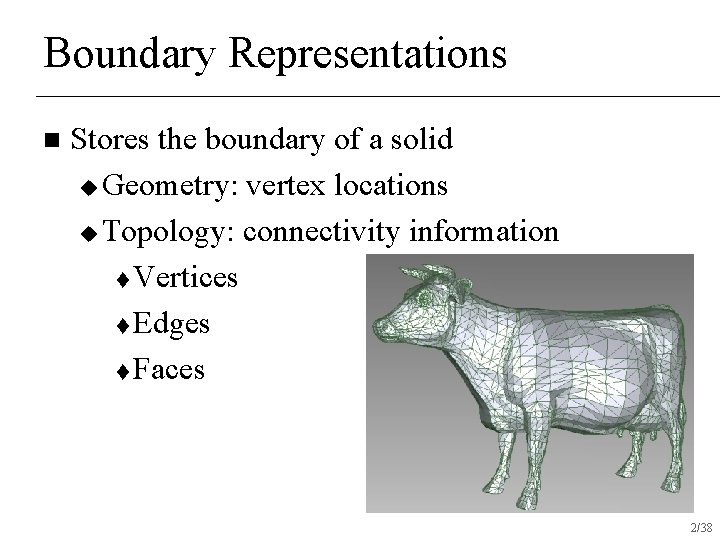
Boundary Representations n Stores the boundary of a solid u Geometry: vertex locations u Topology: connectivity information t Vertices t Edges t Faces 2/38

Boundary Representations n Constant time adjacency information u For each vertex, t Find edges/faces touching vertex u For each edge, t Find vertices/faces touching edge u For each face, t Find vertices/edges touching face 3/38

Boundary Representations n Typically assume the surface is manifold n A surface is manifold if, for every point, locally the surface is equivalent to an open disk 4/38

Boundary Representations n Typically assume the surface is manifold n A surface is manifold if, for every point, locally the surface is equivalent to an open disk Locally manifold 5/38

Boundary Representations n Typically assume the surface is manifold n A surface is manifold if, for every point, locally the surface is equivalent to an open disk Non-manifold edge 6/38

Boundary Representations n Typically assume the surface is manifold n A surface is manifold if, for every point, locally the surface is equivalent to an open disk Non-manifold vertex 7/38

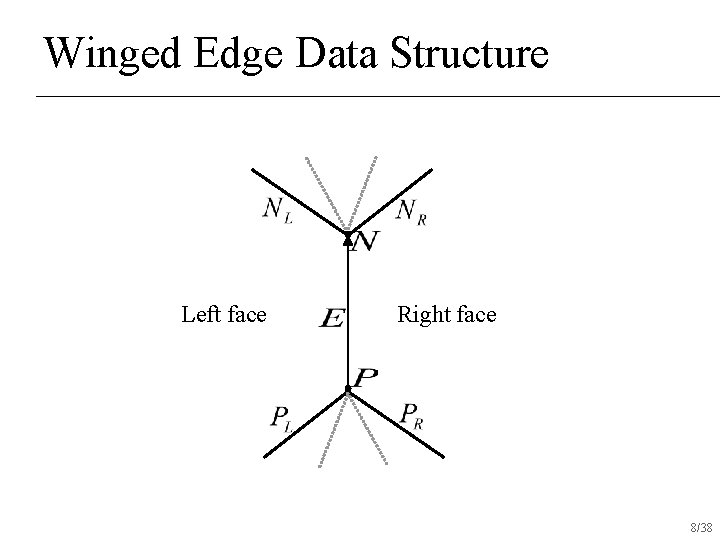
Winged Edge Data Structure Left face Right face 8/38

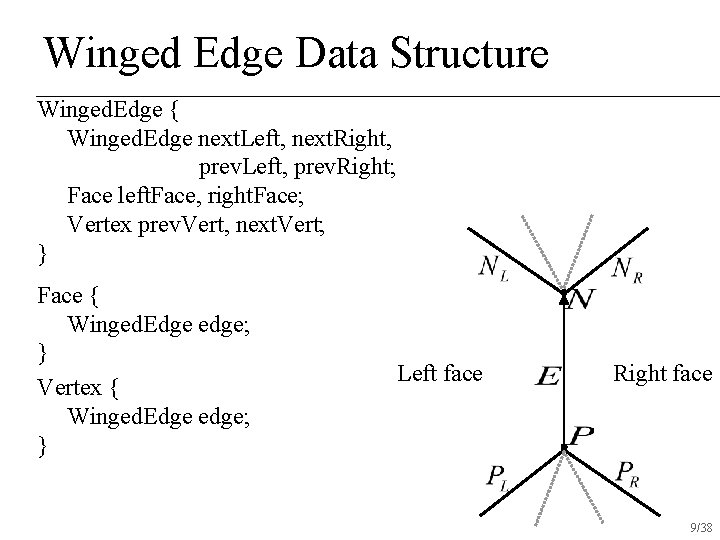
Winged Edge Data Structure Winged. Edge { Winged. Edge next. Left, next. Right, prev. Left, prev. Right; Face left. Face, right. Face; Vertex prev. Vert, next. Vert; } Face { Winged. Edge edge; } Vertex { Winged. Edge edge; } Left face Right face 9/38

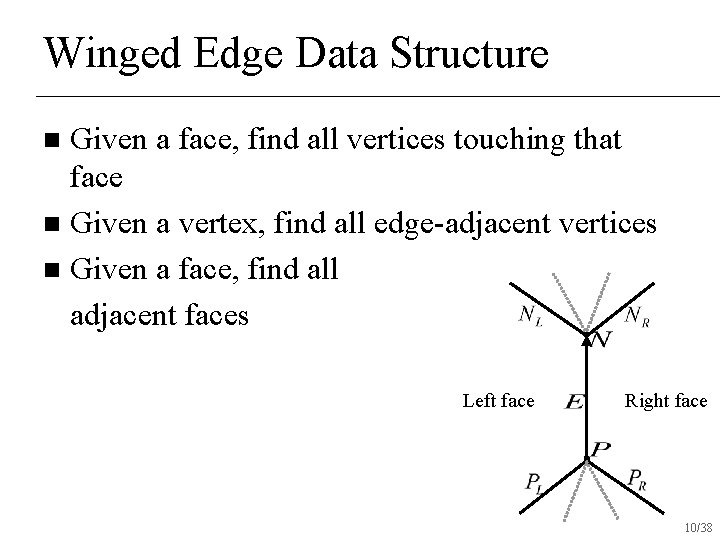
Winged Edge Data Structure Given a face, find all vertices touching that face n Given a vertex, find all edge-adjacent vertices n Given a face, find all adjacent faces n Left face Right face 10/38

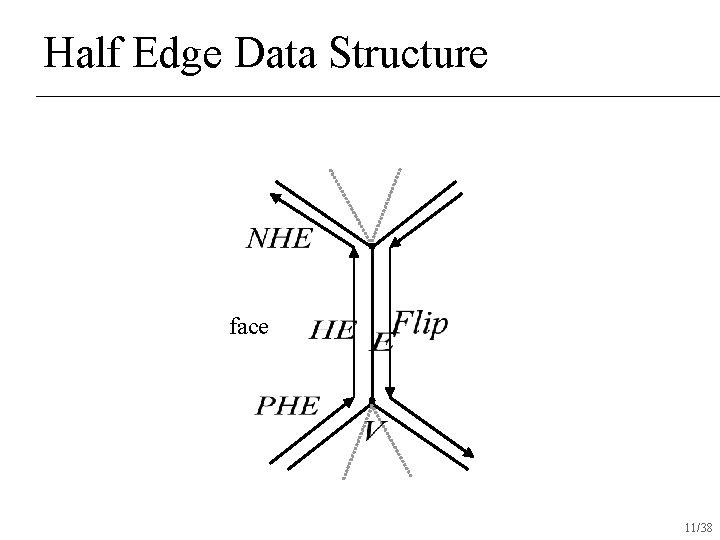
Half Edge Data Structure face 11/38

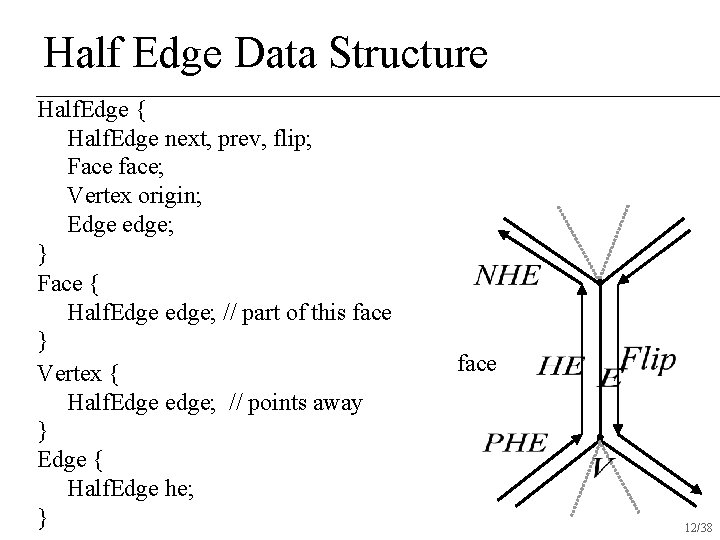
Half Edge Data Structure Half. Edge { Half. Edge next, prev, flip; Face face; Vertex origin; Edge edge; } Face { Half. Edge edge; // part of this face } Vertex { Half. Edge edge; // points away } Edge { Half. Edge he; } face 12/38

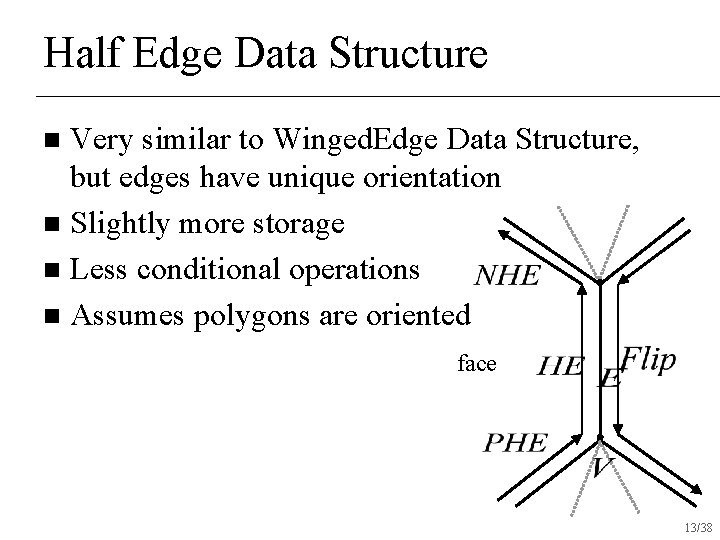
Half Edge Data Structure Very similar to Winged. Edge Data Structure, but edges have unique orientation n Slightly more storage n Less conditional operations n Assumes polygons are oriented n face 13/38

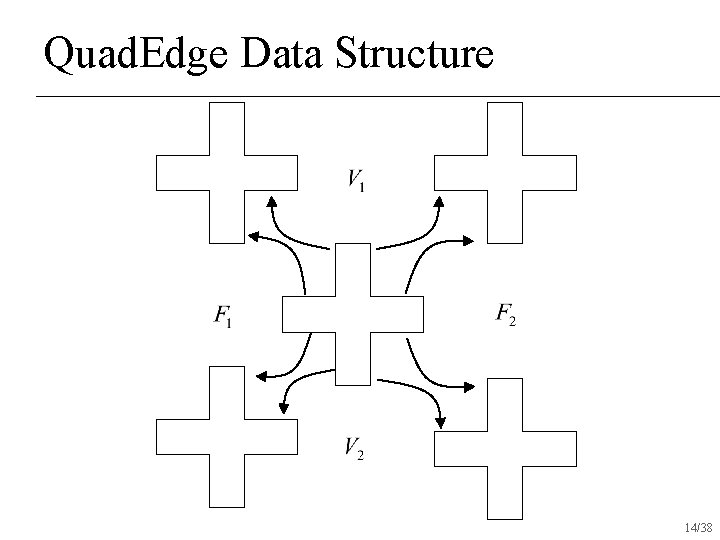
Quad. Edge Data Structure 14/38

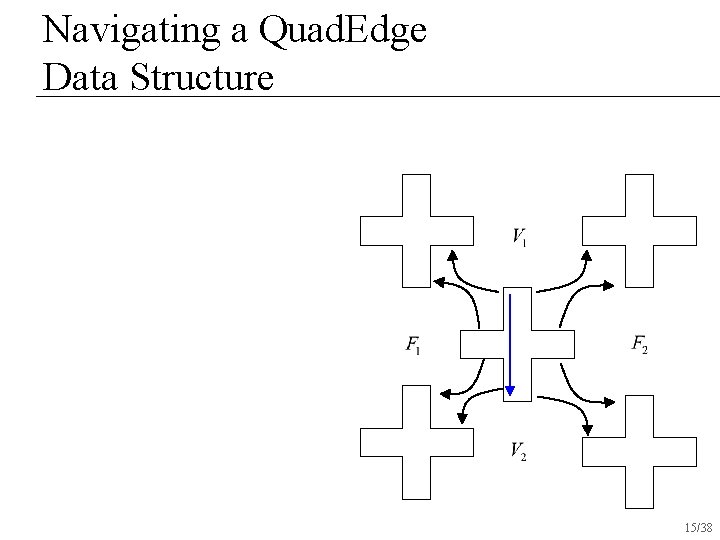
Navigating a Quad. Edge Data Structure 15/38

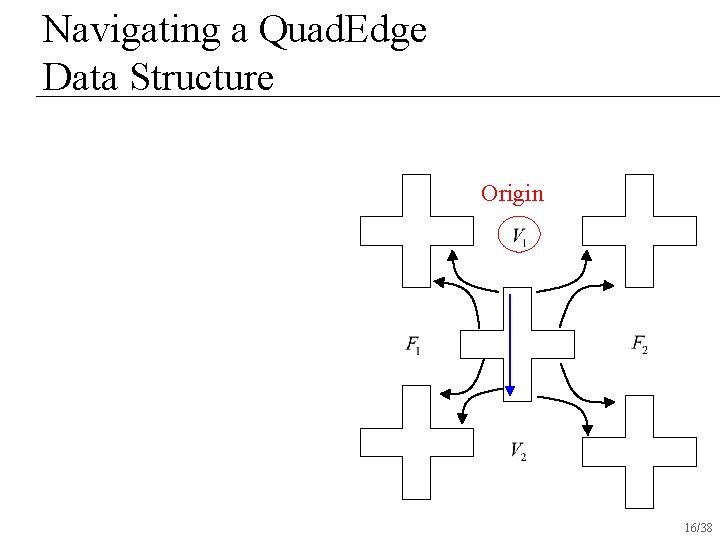
Navigating a Quad. Edge Data Structure Origin 16/38

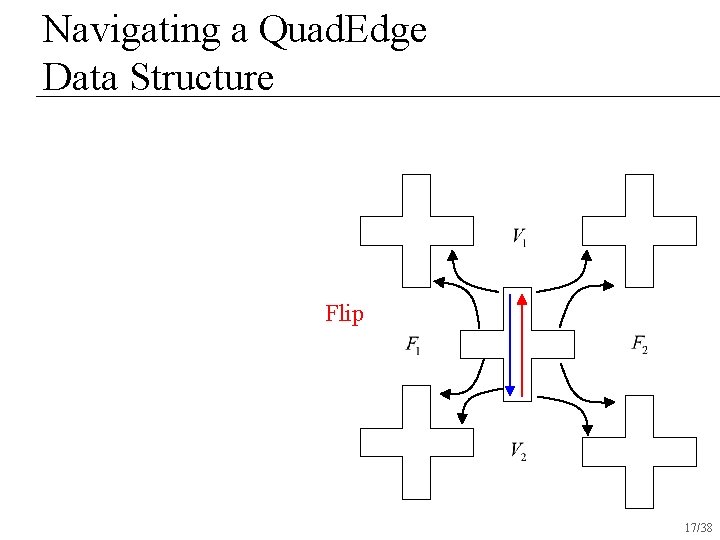
Navigating a Quad. Edge Data Structure Flip 17/38

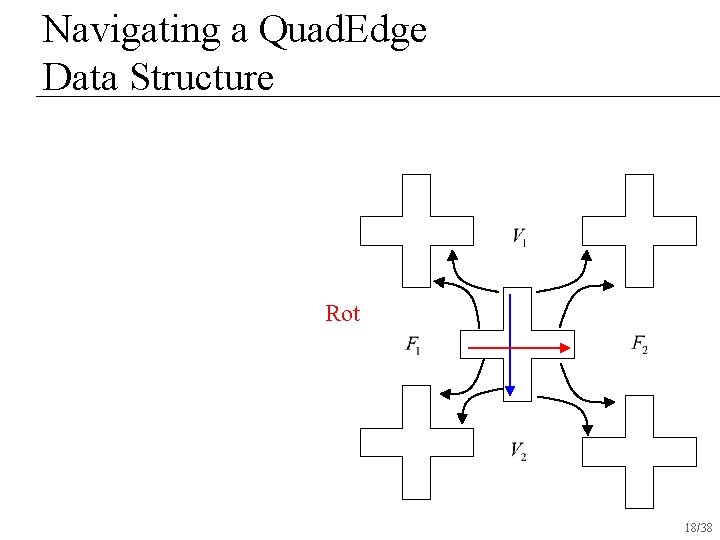
Navigating a Quad. Edge Data Structure Rot 18/38

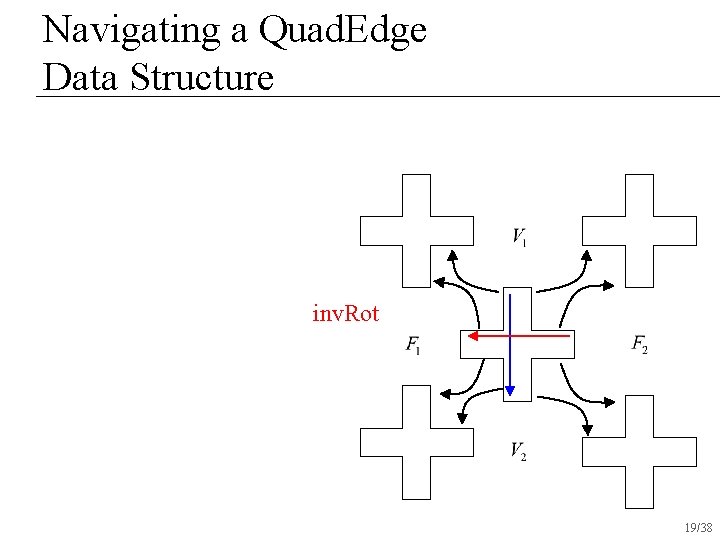
Navigating a Quad. Edge Data Structure inv. Rot 19/38

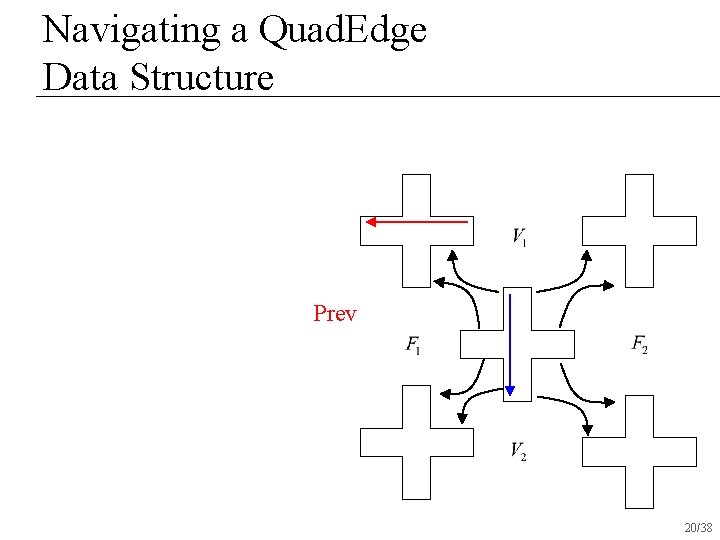
Navigating a Quad. Edge Data Structure Prev 20/38

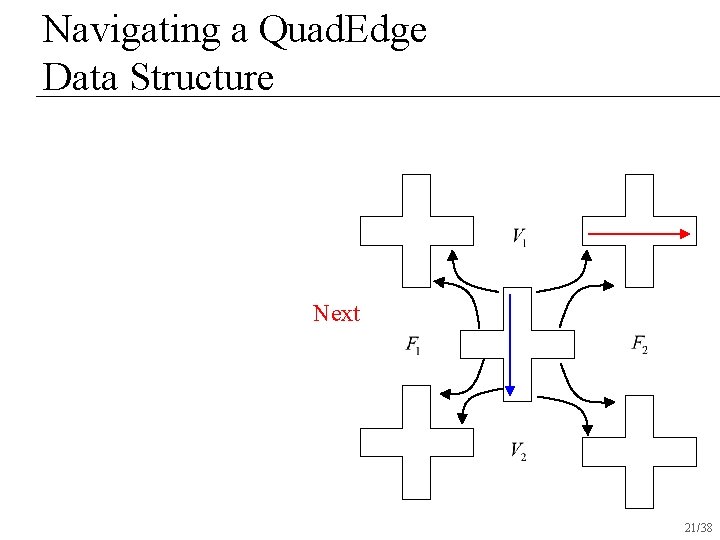
Navigating a Quad. Edge Data Structure Next 21/38

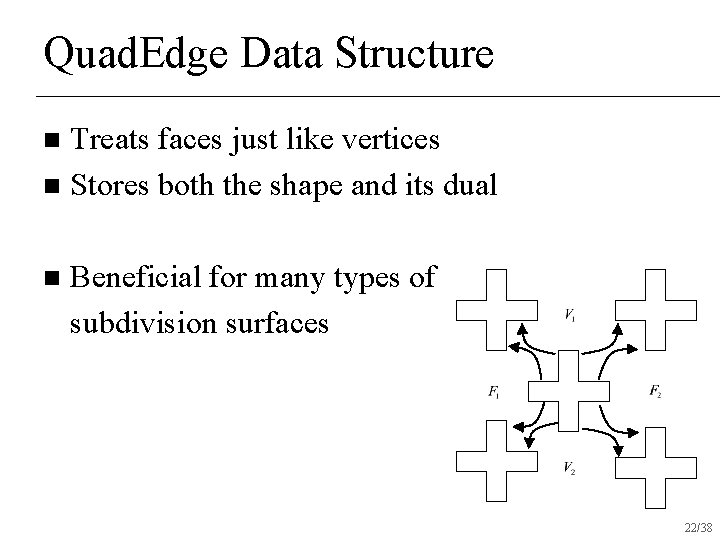
Quad. Edge Data Structure Treats faces just like vertices n Stores both the shape and its dual n n Beneficial for many types of subdivision surfaces 22/38

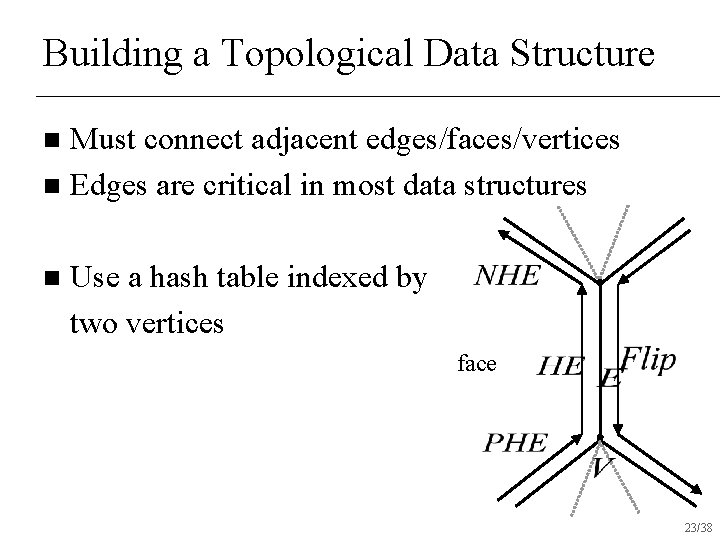
Building a Topological Data Structure Must connect adjacent edges/faces/vertices n Edges are critical in most data structures n n Use a hash table indexed by two vertices face 23/38

Euler Characteristic V: number of vertices n E: number of edges n F: number of faces n G: genus of surface (number of holes) n 24/38

Euler Characteristic V: number of vertices n E: number of edges n F: number of faces n G: genus of surface (number of holes) n 25/38

Euler Characteristic V: number of vertices n E: number of edges n F: number of faces n G: genus of surface (number of holes) n 26/38

Euler Characteristic V: number of vertices n E: number of edges n F: number of faces n G: genus of surface (number of holes) n 27/38

Euler Characteristic V: number of vertices n E: number of edges n F: number of faces n G: genus of surface (number of holes) n 28/38

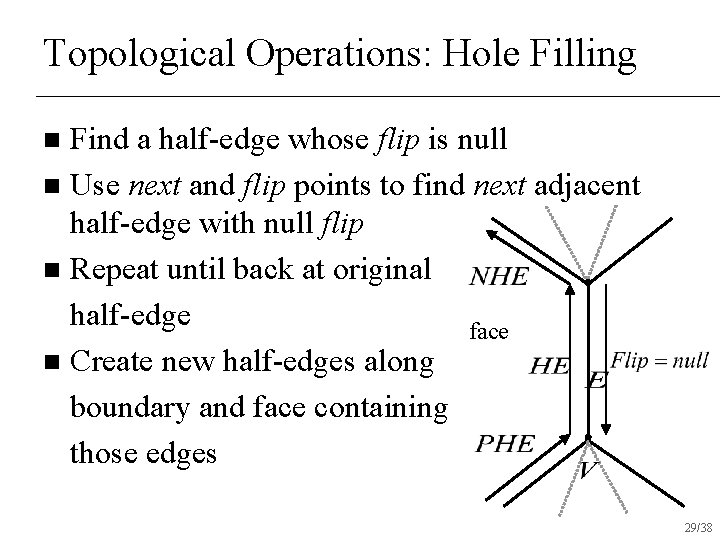
Topological Operations: Hole Filling Find a half-edge whose flip is null n Use next and flip points to find next adjacent half-edge with null flip n Repeat until back at original half-edge face n Create new half-edges along boundary and face containing those edges n 29/38

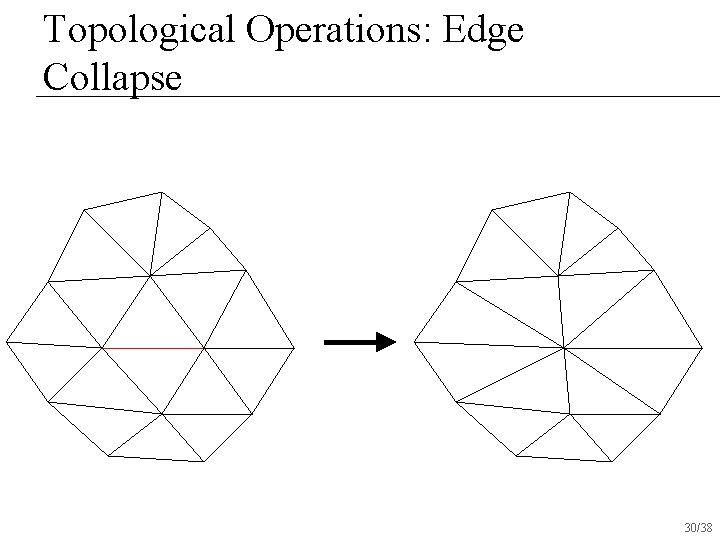
Topological Operations: Edge Collapse 30/38

Topological Operations: Edge Collapse n Set origin of all edges pointing outwards from two vertices to new vertex and vertex to one of the half-edges 31/38

Topological Operations: Edge Collapse n n Set origin of all edges pointing outwards from two vertices to new vertex and vertex to one of the half-edges Set flip on outer edges to point to opposite edge 32/38

Topological Operations: Edge Collapse n n n Set origin of all edges pointing outwards from two vertices to new vertex and vertex to one of the half-edges Set flip on outer edges to point to opposite edge Make sure half-edge pointer for edges point to correct half-edge and vice versa 33/38

Topological Operations: Edge Collapse n n Set origin of all edges pointing outwards from two vertices to new vertex and vertex to one of the half-edges Set flip on outer edges to point to opposite edge Make sure half-edge pointer for edges point to correct half-edge and vice versa Update half-edge for wing-vertices 34/38

Topological Operations: Edge Collapse n n n Set origin of all edges pointing outwards from two vertices to new vertex and vertex to one of the half-edges Set flip on outer edges to point to opposite edge Make sure half-edge pointer for edges point to correct half-edge and vice versa Update half-edge for wing-vertices Delete faces/edges/vertices 35/38

Topological Operation: Edge Collapse n Edge collapse preserves topology as long as the local Euler characteristic of the surface remains the same 36/38

Topological Operation: Edge Collapse n Edge collapse preserves topology as long as the local Euler characteristic of the surface remains the same 37/38

Topological Operation: Edge Collapse n Edge collapse does NOT always preserve topology 38/38

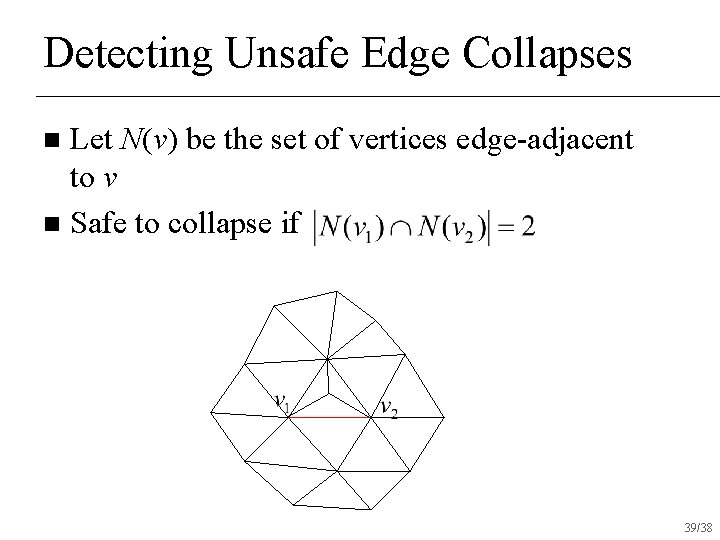
Detecting Unsafe Edge Collapses Let N(v) be the set of vertices edge-adjacent to v n Safe to collapse if n 39/38