Boundary Element Method Introduction Stephen Kirkup School of

Boundary Element Method Introduction Stephen Kirkup School of Engineering, University of Central Lancashire, England

Purpose • The Boundary Element Method is a Numerical Method • From a mathematical viewpoint the BEM finds an approximate solution to a partial differential equation (PDE) governing a domain • For an engineer the BEM can be used to simulate the properties of a design before committing the building the prototyp • Domain of ‘just about any reasonable’ shape and general conditions • Analytic methods only work for simple separable geometries - eg circles, squares, spheres and cylinders. Useful for generating test problems.

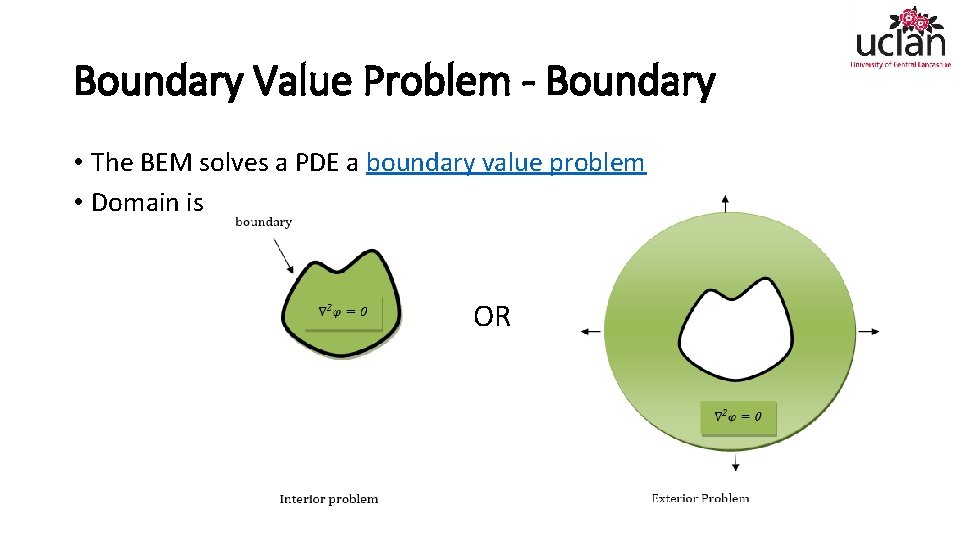
Boundary Value Problem - Boundary • The BEM solves a PDE a boundary value problem • Domain is OR

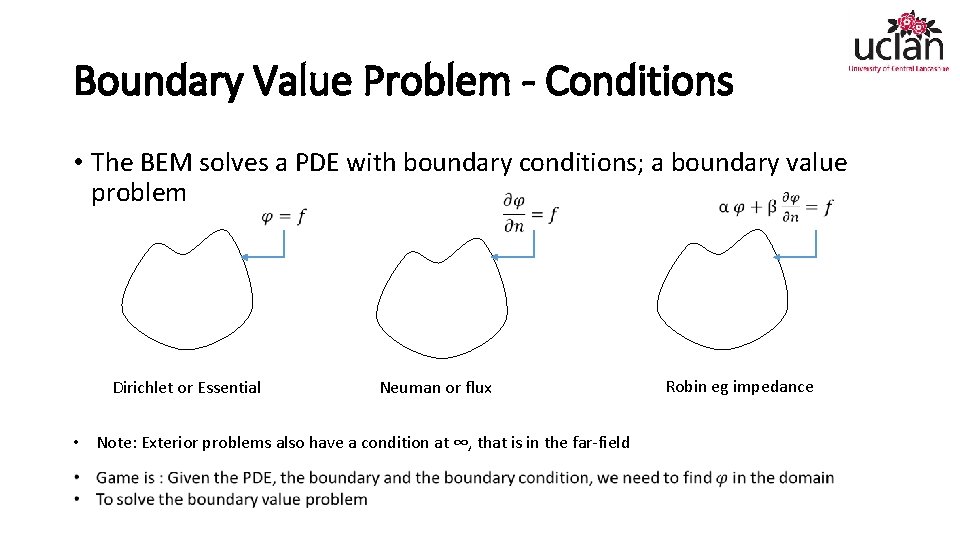
Boundary Value Problem - Conditions • The BEM solves a PDE with boundary conditions; a boundary value problem Dirichlet or Essential Neuman or flux • Note: Exterior problems also have a condition at ∞, that is in the far-field Robin eg impedance

Motivation • Finite element method and the finite difference method? FDM: 27 internal nodes FEM: 42 elements BEM: 16 elements • Finer Mesh? • BEM is possibly more efficient to scale • 3 D? • Only the surface needs to be meshed – benefits of BEM seem more pronounced • Ease of use? • Boundary mesh is ‘easier’ or ‘less bother’ to set up than a domain mesh

Motivation - FEM for exterior problems • Possible Solution – Infinite elements

Motivation - FDM for exterior problems • Possible Solution – Perfectly matched layer

Motivation - BEM for exterior problems

Initial Summary • In the boundary element method only a boundary mesh is required • Hence possibly a lot less elements or nodes – possible efficiency saving • Possible reduction in run time • Less ‘bother’ in comparison to the other methods • Saves development time for the eventual user – typically an engineer • Raises the profile of the BEM as a teaching package • An important research area in humble SK’s view and one that has been largely overlooked • Requires a reformulation of the PDE as a boundary-only equation • Can be done for some linear elliptic PDEs • Quite a restriction although some progress with DRM/MRM

BEM in Practice • Is used in most areas of physics/engineering, but not as widely as FEM • Can be thought of as a competitor to the FEM or FDM • More realistic to see it as a complement to these methods • Could be thought of as an alternative to PML or infinite BEM elements for exterior problems FEM/FDM • In a ‘multiphysics’ situation, the preferred method could be used in each domain BEM eg fluid-structure BEM-FEM

Wot? Still not much maths? • Where are we coming from? • Mathematician or Engineer? • Researcher, Teacher or Student? • How do I learn about the method? • Mathematical basis of BEM is complicated • Traditionally, books on BEM are impenetrable • Educational viewpoint in SK’s humble opinion • Work towards making BEM theory accessible and inclusive • Easy to use the method and so educational possiblities within and outside of BEM world

This week • Develop the BEM for the solution of Laplace’s equation • Simplest equation to which the BEM can be applied • Is widely applicable in physics and engineering: ‘potential’ problems • The model equation for the BEM • Most problems you find with the application of the BEM to any other problem area will be found in this one • It is the best equation with which we learn and teach the BEM and …. • Develop the BEM for the solution of the Helmholtz Equation • Acoustics • Eigenvalue Problems • Fluid-Structure Interaction