BOTTOMUP FORMAL VALIDATION VERIFI CATION OF BINARYSPECIFIC SOFTWARE

BOTTOM-UP FORMAL VALIDATION VERIFI CATION OF BINARY-SPECIFIC SOFTWARE PROPERTIES DR. KEVIN HAMLEN EUGENE MCDERMOTT PROFESSOR COMPUTER SCIENCE DEPARTMENT CYBER SECURITY RESEARCH AND EDUCATION INSTITUTE THE UNIVERSITY OF TEXAS AT DALLAS Supported in part by: AFOSR Award FA 750 -15 -C-0066, ONR Award N 00014 -14 -1 -0030, DARPA Award FA 8750 -19 -C-0006, NSF Award 1513704 and an NSF I/UCRC Award from Lockheed Martin Any opinions, findings, conclusions, or recommendations expressed in this presentation are those of the author(s) and do not necessarily reflect the views of the ONR, NSF, DARPA, or Lockheed Martin.

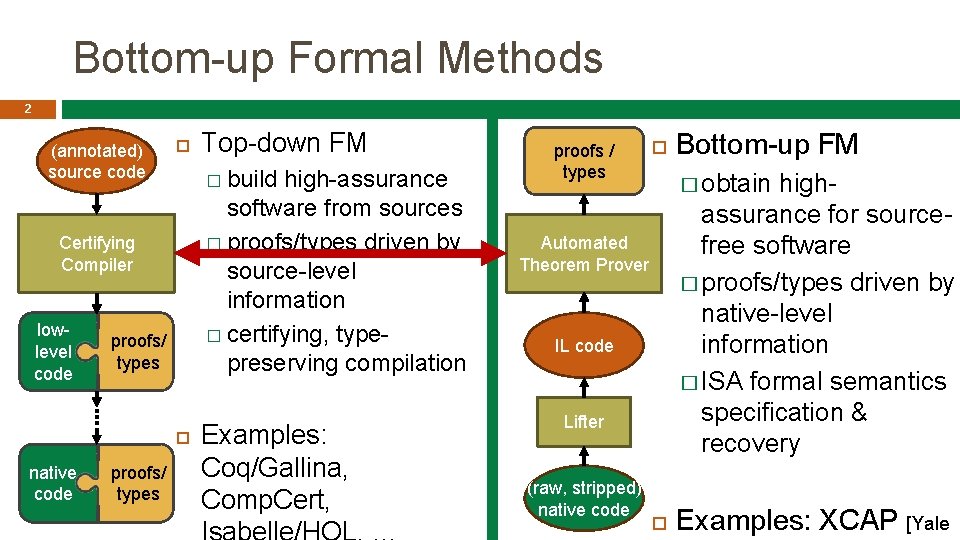
Bottom-up Formal Methods 2 (annotated) source code � build high-assurance software from sources � proofs/types driven by source-level information � certifying, typepreserving compilation Certifying Compiler lowlevel code proofs/ types native code proofs/ types Top-down FM Examples: Coq/Gallina, Comp. Cert, proofs / types � obtain highassurance for sourcefree software � proofs/types driven by native-level information � ISA formal semantics specification & recovery Automated Theorem Prover IL code Lifter (raw, stripped) native code Bottom-up FM Examples: XCAP [Yale

Why Bottom-up? 3 Prevalence of source-free code hand-written assembly � native libraries derived from unverifiable source languages � native libraries generated by unverified/unknown tools � closed-source software products in mission-critical environments � Automated Theorem Prover Formal verification of low-level tools loaders, linkers, compilers, … � reverse-engineering tools (e. g. , decompilers) � virtual machines, kernels, hypervisors, … � proofs / types Reasoning about native code analyses & transformations binary-level control-flow integrity algorithms � security hotpatching � polymorphic malware defenses IL code Lifter � (raw, stripped) native code

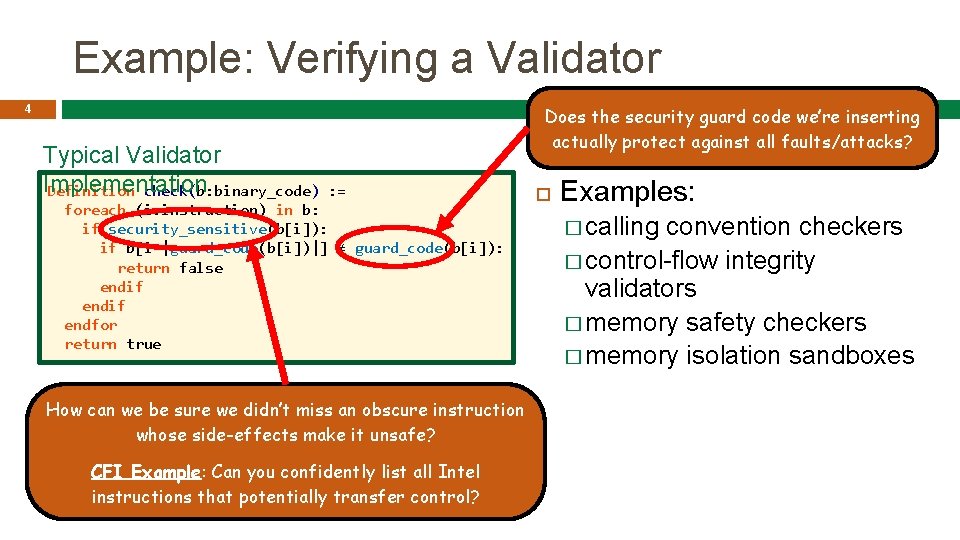
Example: Verifying a Validator 4 Typical Validator Implementation Definition check(b: binary_code) Does the security guard code we’re inserting actually protect against all faults/attacks? : = foreach (i: instruction) in b: if security_sensitive(b[i]): if b[i-|guard_code(b[i])|] ≠ guard_code(b[i]): return false endif endfor return true How can we be sure we didn’t miss an obscure instruction whose side-effects make it unsafe? CFI Example: Can you confidently list all Intel instructions that potentially transfer control? Examples: � calling convention checkers � control-flow integrity validators � memory safety checkers � memory isolation sandboxes

Example: Verifying a Validator 5 Typical Validator Implementation Definition check(b: binary_code) : = foreach (i: instruction) in b: if security_sensitive(b[i]): if b[i-|guard_code(b[i])|] ≠ guard_code(b[i]): return false endif Universally quantified property of endif binary code! (Requires a fairly endfor complete model of the ISA. ) return true Property to Formally Validate: Examples: � calling convention checkers � control-flow integrity validators � memory safety checkers � memory isolation sandboxes non-deterministic! (b: binary_code), check(b) = true -> (σ σ : cpu_state), good_state(σ) -> σ b(σ) -> good_state(σ )

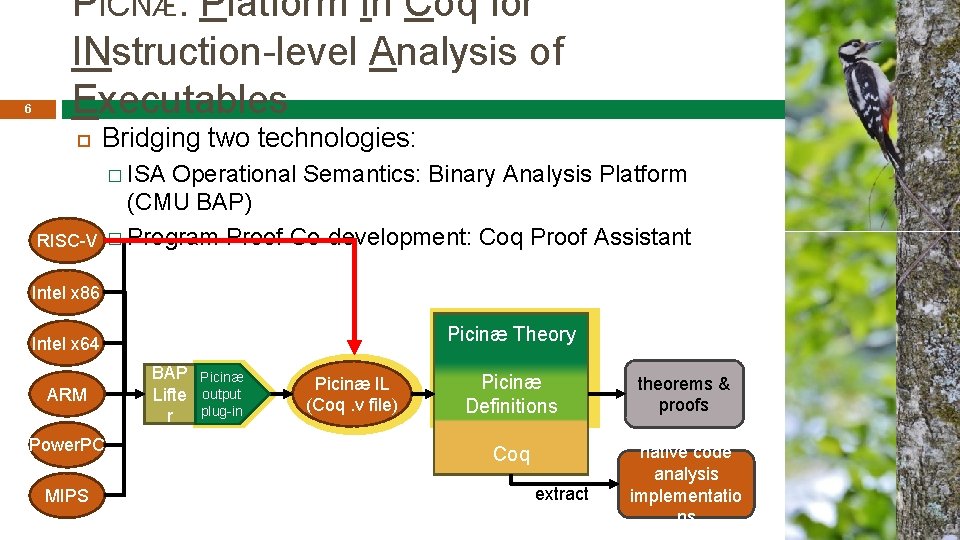
6 PICNÆ: Platform In Coq for INstruction-level Analysis of Executables Bridging two technologies: � ISA RISC-V Operational Semantics: Binary Analysis Platform (CMU BAP) � Program Proof Co-development: Coq Proof Assistant Intel x 86 Picinæ Theory Intel x 64 ARM Power. PC MIPS BAP Lifte r Picinæ output plug-in Picinæ IL (Coq. v file) Picinæ Definitions theorems & proofs Coq native code analysis implementatio ns extract

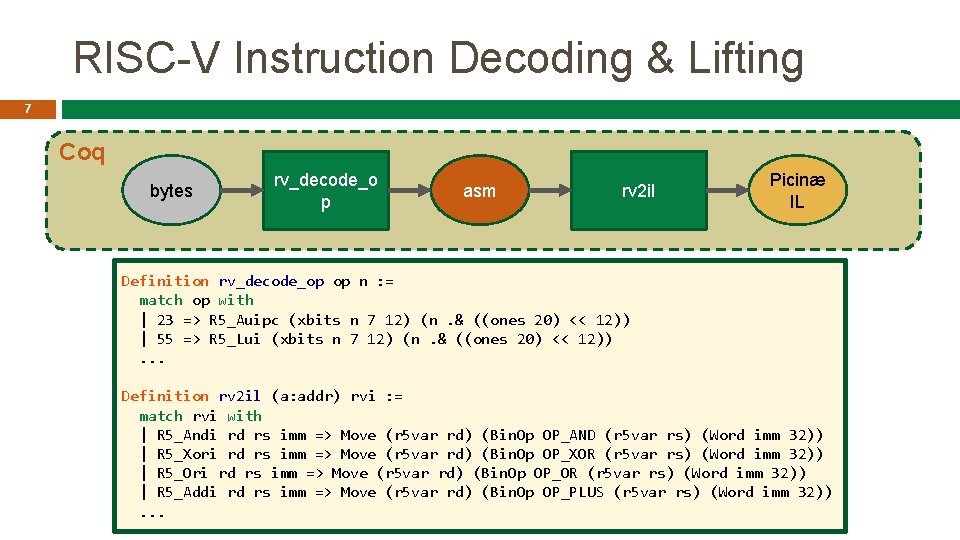
RISC-V Instruction Decoding & Lifting 7 Coq bytes rv_decode_o p asm rv 2 il Picinæ IL Definition rv_decode_op op n : = match op with | 23 => R 5_Auipc (xbits n 7 12) (n. & ((ones 20) << 12)) | 55 => R 5_Lui (xbits n 7 12) (n. & ((ones 20) << 12)). . . Definition rv 2 il (a: addr) rvi : = match rvi with | R 5_Andi rd rs imm => Move (r 5 var rd) (Bin. Op OP_AND (r 5 var rs) (Word imm 32)) | R 5_Xori rd rs imm => Move (r 5 var rd) (Bin. Op OP_XOR (r 5 var rs) (Word imm 32)) | R 5_Ori rd rs imm => Move (r 5 var rd) (Bin. Op OP_OR (r 5 var rs) (Word imm 32)) | R 5_Addi rd rs imm => Move (r 5 var rd) (Bin. Op OP_PLUS (r 5 var rs) (Word imm 32)). . .

Project Objectives 8 Reason about near arbitrary native code without appeal to source-derived meta-data (e. g. , invariants, CFGs, debug info, or disassembly maps) ISA-general, machine-checked theory � support for cross-ISA software analysis minimal trusted computing base � minimal semantic gap between native code and IL code � minimal base of trusted definitions approachable by Coq novices � ~250 lines of core definitions (functions + propositions) � ~300 theorems (searchable on as-needed basis) Reason about code transformation algorithms � native code can be an unknown in the proof

Project Scope 9 Out of Scope � Validating/deriving the native-to-IL lifting � Modeling hardware details � Picinæ IL semantics resemble a Von Neumann / Harvard machine no caching effects, no multicore modeling, etc. (yet? ) Unhandled hardware exception control-flows no comprehensive, machine-readable spec of many ISAs Picinæ IL targetable by many lifting strategies Supportable, but significantly complicates other analyses Possibly a future extension Supported features � � � instruction aliasing (e. g. , misaligned instructions on Intel ISAs) dynamic changes to page access permissions (readable/writable) localized reasoning about memory (separation logic) undefined processor elements (non-determinism) self-modifying code (supported in theory; requires Coq port of instruction decoder)

IL Encoding 11 Programs Definition program : = addr -> option (N * stmt). Statements (one per machine instruction) Inductive stmt : = | | | | Expressions (effect-free) Inductive exp : = | Var (v: var) | Word (n: N) (w: bitwidth) | Load (e 1 e 2: exp) (en: endianness) (w: bitwidth) | Store (e 1 e 2 e 3: exp) (en: endianness) (w: bitwidth) | Bin. Op (b: binop_typ) (e 1 e 2: exp) | Un. Op (u: unop_typ) (e: exp) | Cast (c: cast_typ) (w: bitwidth) (e: exp) | Let (v: var) (e 1 e 2: exp) | Unknown (w: bitwidth). Nop (* Do nothing. *) Move (v: var) (e: exp) (* Assign to variable. *) Jmp (e: exp) (* Jump to a label/address. *) Exn (i: N) (* CPU Exception (numbered) *) Seq (q 1 q 2: stmt) (* sequence: q 1 then q 2 *) If (e: exp) (q 1 q 2: stmt) (* If e<>0 then q 1 else q 2 *) Rep (e: exp) (q: stmt) (* Repeat q for e iterations *).

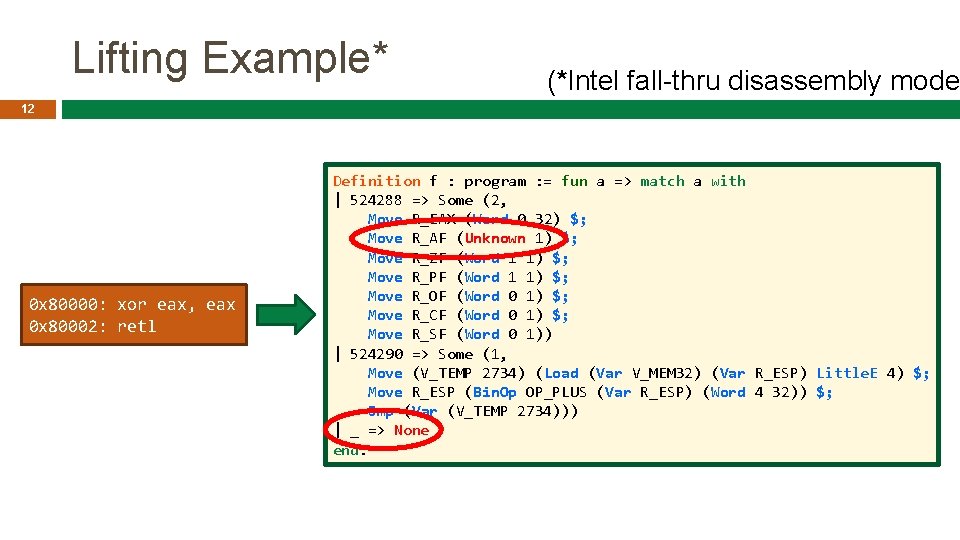
Lifting Example* (*Intel fall-thru disassembly mode 12 0 x 80000: xor eax, eax 0 x 80002: retl Definition f : program : = fun a => match a with | 524288 => Some (2, Move R_EAX (Word 0 32) $; Move R_AF (Unknown 1) $; Move R_ZF (Word 1 1) $; Move R_PF (Word 1 1) $; Move R_OF (Word 0 1) $; Move R_CF (Word 0 1) $; Move R_SF (Word 0 1)) | 524290 => Some (1, Move (V_TEMP 2734) (Load (Var V_MEM 32) (Var R_ESP) Little. E 4) $; Move R_ESP (Bin. Op OP_PLUS (Var R_ESP) (Word 4 32)) $; Jmp (Var (V_TEMP 2734))) | _ => None end.

Operational Semantics (18 rules) 13 Expressio ns: Statement s: Program s:

Picinæ Theory 14 Functional Interpreter � Static Semantics � � � Converts IL expressions to Coq theories of N and Z Facilitates verification of machine operations that conflate signed+unsigned ops Monotonicity & Frame Theorems � Floyd-Hoare style inductive proofs of partial and total correctness Theory of two’s complement � Proves type-soundness of lifted IL code Implies basic well-formedness properties of register/memory values Inductive proof principles � Implements IL semantics as a deterministic function for faster symbolic interpretation (~600% faster than tactics) Proofs completed with partial info about cpu+program state hold extensionally Separation Logic � Deep embedding of Frame Axiom for localized memory reasoning about data structures

ISA Modularity via Dependent Typing 15 IL semantics implemented as a Coq Functor parameterized by an ISA 1 specification Inductive x 86 var : = 2 3 4 5 6 7 | MEM 32 (* main memory *) | AF | CF | DF | OF | PF | SF | ZF (* flags *) | EAX | EBX | ECX | EDI | ESI (* general-purpose registers *). . . | A_READ | A_WRITE (* page access permission bits *) | V_TEMP (n: N) (* temporaries (introduced by lifter) *). 8 Module X 86 Arch <: Architecture. 9 Module Var : = Make_UDT Mini. X 86 Var. Eq. 10 Definition mem_bits : = 8. 11 Definition mem_readable s a : = exists r, s A_READ = Some (Va. M r 32) / r a <> 0. 12 Definition mem_writable s a : = exists w, s A_WRITE = Some (Va. M w 32) / w a <> 0. 13 Theorem mem_readable_mono: forall s 1 s 2 a, s 1 ⊆ s 2 -> mem_readable s 1 a -> mem_readable s 2 a. 14 Proof. intros. destruct H 0. eexists. split; [apply H|]; apply H 0. Qed. 15 Theorem mem_readable_mono: forall s 1 s 2 a, s 1 ⊆ s 2 -> mem_writable s 1 a -> mem_writable s 2 a. 16 Proof. intros. destruct H 0. eexists. split; [apply H|]; apply H 0. Qed. 17 End X 86 Arch.

16 Verifying Binary Properties of se. L 4 Microkernel Proof goals currently in progress: � functional adherence to architectural calling conventions: preservation of callee-save registers restoration of stack pointer weakest precondition for return address integrity � total correctness validation of low-level libraries string/memory manipulation library routines (e. g. , memset) Main challenge: Low-level library code is aggressively optimized in ways not typically found at source code level or even in automated compiler optimizations

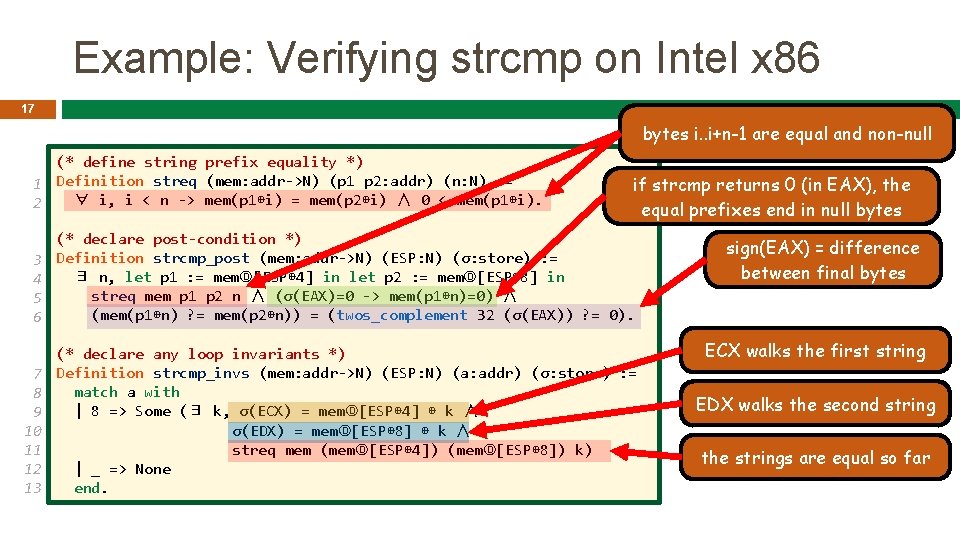
Example: Verifying strcmp on Intel x 86 17 bytes i. . i+n-1 are equal and non-null (* define string prefix equality *) 1 Definition streq (mem: addr->N) (p 1 p 2: addr) (n: N) : = ∀ i, i < n -> mem(p 1⊕i) = mem(p 2⊕i) ∧ 0 < mem(p 1⊕i). 2 if strcmp returns 0 (in EAX), the equal prefixes end in null bytes 3 4 5 6 (* declare post-condition *) Definition strcmp_post (mem: addr->N) (ESP: N) (σ: store) : = ∃ n, let p 1 : = memⒹ[ESP⊕ 4] in let p 2 : = memⒹ[ESP⊕ 8] in streq mem p 1 p 2 n ∧ (σ(EAX)=0 -> mem(p 1⊕n)=0) ∧ (mem(p 1⊕n) ? = mem(p 2⊕n)) = (twos_complement 32 (σ(EAX)) ? = 0). 7 8 9 10 11 12 13 (* declare any loop invariants *) Definition strcmp_invs (mem: addr->N) (ESP: N) (a: addr) (σ: store) : = match a with | 8 => Some (∃ k, σ(ECX) = memⒹ[ESP⊕ 4] ⊕ k ∧ σ(EDX) = memⒹ[ESP⊕ 8] ⊕ k ∧ streq mem (memⒹ[ESP⊕ 4]) (memⒹ[ESP⊕ 8]) k) | _ => None end. sign(EAX) = difference between final bytes ECX walks the first string EDX walks the second string the strings are equal so far

Example: Verifying strcmp on Intel x 86 18 1 Theorem strcmp_correctness (entrypoint: addr): ∀ (σ σ : store) (mem: addr->N) (n: N) (x: exit_condition), 2 models x 86 typctx σ -> σ(MEM) = mem -> 3 valid_return_address (σ(memⒹ[σ(ESP)])) -> 4 exec_prog strcmp entrypoint σ n σ x), 5 all_invariants_hold (strcmp_invset mem (σ(ESP)) strcmp σ ). 6 7 Proof. (*. . . 27 lines of proof. . . *) … 35 Qed.

Some Preliminary Take-aways 19 Aggressive optimization is the biggest challenge. � � Much more powerful validation feasible on RISC-V than on other ISAs � � � ARM: optimizations heavily use conditional instructions, which results in massively complex CFGs Intel: CISC ISA means many optimizations use bizarre side-effects of obscure instructions (e. g. , parity flag) RISC-V instruction decoder much easier to formalize than other ISAs! More powerful automated theory of 2’s complement binary arithmetic needed for Coq � Example: ((~x) xor (x - 0 x 0101)) & 0 x 01010100 = 0 iff x contains no zero-bytes (? ? ? ) Level-agnostic: Verification difficulty is about the same whether the optimization is expressed at the source or binary level. (But binary code tends to be more aggressively optimized than source. ) w + n 1 – n 2) mod 2 w Example: n 1 ⊖ n 2 = (2 Coq’s dependent type system is enormously helpful relative to non-dependent proof systems

Summary 20 Picinæ bridges two important technologies: ISA semantic-lifters (e. g. , BAP) � automated theorem provers / proof assistants (Coq) � Improvements over prior works � Prove properties of near arbitrary native code � No reliance on source semantics � not just the ISA subset produced by some particular compiler Binary might have been generated by source-less tools (e. g. , binary hotpatching, macro assembler) Source semantics still usable to infer proof steps (e. g. , invariants) Suitable for verifying properties of binary code transforms Substantial theory � static semantics (progress, preservation), Floyd-Hoare induction, symbolic interpretation, separation logic, sign-unknown binary arithmetic, non-determinism, monotonic reasoning

Forthcoming paper 21 Kevin W. Hamlen, Dakota Fisher, and Gilmore Lundquist. Source-free Machine-checked Validation of Native Code in Coq. In Proc. of the 3 rd Workshop on Forming an Ecosystem Around Code Transformation (FEAST), November 2019 (co-located with ACM CCS, forthcoming).