BOSHLANGICH MATEMATIKA KURSI NAZARIYASI FANIDAN TAQDIMOT 17 Mavzu

“BOSHLANG`ICH MATEMATIKA KURSI NAZARIYASI” FANIDAN TAQDIMOT 17 -Mavzu: Mulohazalar va ular ustida amallar. Bilim sohasi: 100000 – gumanitar soha Ta’lim sohasi: 110000 - pedagogika Bakavriat yo’nalishi: 5111700 – boshlang’ich ta’lim va sport- tarbiyaviy ish

Maruza rejasi: Mulohazalar dizyunksiyasi, uning xossalari va rostlik jadvalini. Mulohazalar im’likatsiyasi, uning xossalari va rostlik jadvalini. Mulohazalar ekvivalensiyasi, uning xossalari va rostlik jadvalini.

B. B. B. jadvali (bilaman, bilishni xohlayman, bildim) № Mavzu savoli Bilaman Bilishni Bildim xohlayman 1 2 3 4 2 Mulоhazani inkоrini 3 Mulоhaza kоn’yunksiyasi diz’yunksiyasini 4 Mulоhazalar ustidagi amallarni хоssalarini isbоtlashni va Mulоhaza va 5

Blits-so’rov uchun savollar Mulоhaza nima? Mulоhaza inkоri nima? Mulоhaza kоn’yunksiyasi va diz’yunksiyasi dеb nimaga aytiladi? Mulоhazalar ustidagi amallarni хоssalarini isbоtlab bеring.

Mulohazalar dizyunksiyasi. 1 -ta’rif. Ikkita sodda A, B mulohazalardan tuzilgan «A yoki B» mulohazaga mulohazalar dizyunksiyasi deyiladi. Mulohazalar dizyunksiyasi «A∨B» ko’rinishda yoziladi, «A yoki B» deb o’qiladi va uning tarkibiga kirgan mulohazalarning hech bo’lmaganda bittasi rost bo’lganda, rost bo’ladi. Dizyunksiyaning rostlik jadvali quyidagicha: A B A∨B R R Y Y Y

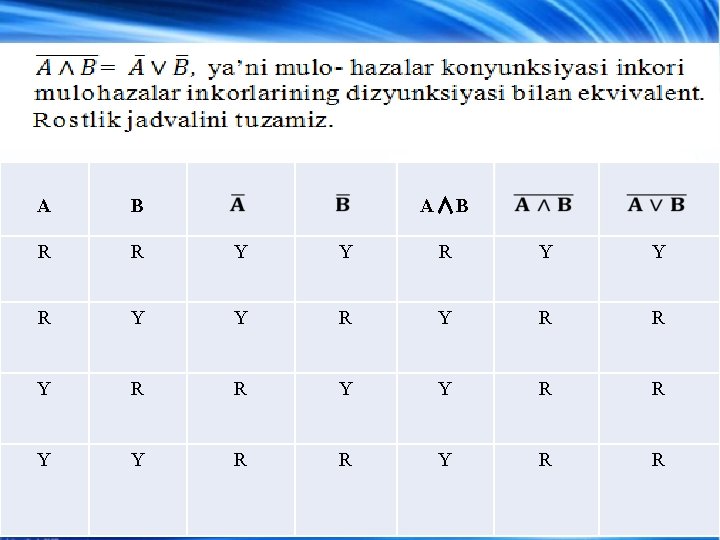
A B A∧B R R Y Y R R Y Y R R

Mulohazalar implikatsiyasi. 2 -ta’rif. Sodda A va B mulohazalardan tuzilgan «Agar. A bo’lsa, B bo’ladi» ko’rinishidagi mulohaza A va B mulohazalarning implikatsiyasi deyiladi va «A⇒B» ko’rinishda belgilanadi.

Mulohazalar implikatsiyasi. A⇒B implikatsiya faqat A rost B yolg’on bo’lgandagina yolg’on bo’ladi. A — im’likatsiya sharti, B — xulosasi deyiladi. A ni B uchun yetarli, B ni A uchun zaruriy shart deb ham ataladi. Im’likatsiyaning rostlik jadvali quyidagicha bo’ladi: A B A⇒B R R Y Y Y R R Y Y R

Implikatsiya turlari.

Mulohazalar ekvivalensiyasi. Thus p ↔ q is true if p and q are either both true or both false. We say that a well-formed proposition is true if its truth-value is true whatever truth-values are assigned to the atomic propositions it contains. Truth tables allow you to determine whether any well-formed proposition is true or false. 14 14 Herbert Gintis. Mathematical Literacy for Humanists. Printed in the United States of America, 2010

Mulohazalar ekvivalensiyasi. 3 -ta’rif. Sodda A va B mulohaialardan tuzilgan «A faqat va faqat B bo’lgandagina bo’ladi» ko ‘rinishdagi mulohaza A va B ning ekvivalensiyasi deyiladi va «A⇔B» ko ‘rinishda yoziladi. A⇔B ekvivalensiya Ava B mulohazalarning qiymatlari bir xil bo’lganda rost bo’ladi.

Ekvivalensiyaning rostlik jadvali: A B A⇔B R R Y Y Y R

Prove them using truth tables, and say what they mean in words. Modus Ponens: (p ˄ (p → q)) → q; Modus Tollens: (p → q) ˄ ¬ q) → ¬ p; ((p → q) ˄ (q → r)) → (p → r); ((p ˅ q) ˄ ¬ p) → q; ((p ˅ q) ˅ r) (p ˅ (q ˅ r)) ((p ˄ q) ˄ r) (p ˄ (q ˄ r)) www. themegallery. com

((p → q) ˄ (r → s) ˄ (p ˅ r)) → (q ˅ s); p ˄ q → p p → p ˅ q ((p → q) ˄ (p → r)) → (p → (q ˄r)); De Morgan’s Theorem I: ¬ (p ˄ q) (¬ p ˅ ¬ q) De Morgan’s Theorem II: ¬ (p ˅ q) (¬ p ˄ ¬ q) Double Negation: ¬¬p p; Distributive I: p ˄ (q ˅ r) (p ˄ q) ˅ (p ˄ r); Distributive II: p ˅ (q ˄ r) (p ˅ q) ˄ (p ˅ r); p ˅ ¬ p. 15 15 Herbert Gintis. Mathematical Literacy for Humanists. Printed in the United States of America, 2010

O‘z-o‘zini tеkshirish uchun savоllar: Mulohazalar dizyunksiyasining ta’rifni va xossasini ayting. ü Mulohazalar dizyunksiyasining rostlik jadvalini ko’rsating. ü Mulohazalar im’likatsiyasining ta’rifni va xossasini ayting. ü Mulohazalar im’likatsiyasining rostlik jadvalini ko’rsating. ü Mulohazalar ekvivalensiyasining ta’rifni va xossasini ayting. ü Mulohazalar ekvivalensiyasining rostlik jadvalini ko’rsating. ü

E’tiboringiz uchun rahmat Thank you for your attention