BoseEinstein Correlations from pp Collisions at RHIC Thomas

Bose-Einstein Correlations from pp Collisions at RHIC Thomas D. Gutierrez University of California, Davis UCD Nuclear Physics Seminar • Introduction • Analysis • Results • Outlook Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 1

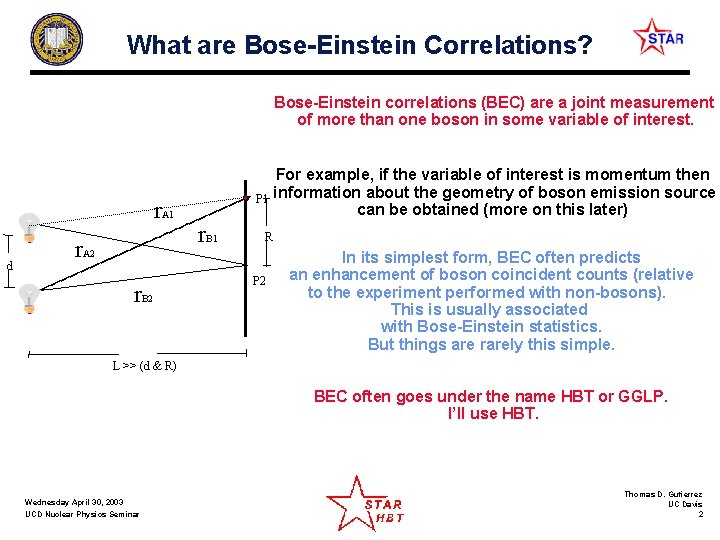
What are Bose-Einstein Correlations? Bose-Einstein correlations (BEC) are a joint measurement of more than one boson in some variable of interest. r. A 1 d r. A 2 r. B 2 For example, if the variable of interest is momentum then P 1 information about the geometry of boson emission source can be obtained (more on this later) r. B 1 R P 2 In its simplest form, BEC often predicts an enhancement of boson coincident counts (relative to the experiment performed with non-bosons). This is usually associated with Bose-Einstein statistics. But things are rarely this simple. L >> (d & R) BEC often goes under the name HBT or GGLP. I’ll use HBT. Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 2

What is HBT? The technique was originally developed by two English astronomers Robert Hanbury-Brown and Richard Twiss (circa 1952) It’s a form of “Intensity Interferometry” -- as opposed to “regular” amplitude-level (Young or Michelson) interferometry -and was used to measure the angular sizes of stars A quantum treatment of HBT generated much controversy and led to a revolution in quantum optics Later it was used by high energy physicists to measure source sizes of elementary particle or heavy ion collisions (the GGLP effect) But how does HBT work? And why use it instead of “regular” interferometry? Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 3

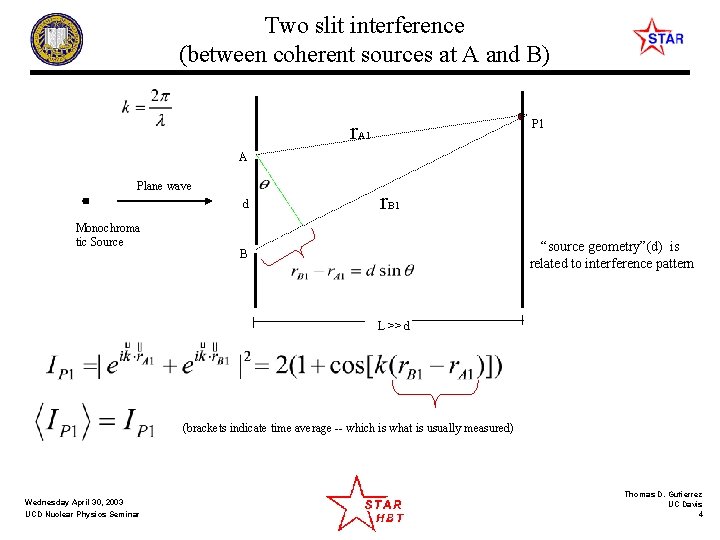
Two slit interference (between coherent sources at A and B) P 1 r. A 1 A Plane wave d Monochroma tic Source r. B 1 “source geometry”(d) is related to interference pattern B L >> d (brackets indicate time average -- which is what is usually measured) Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 4

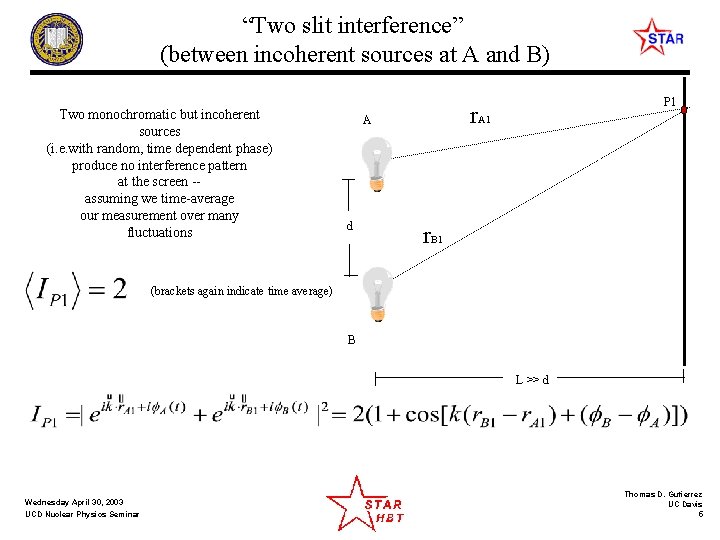
“Two slit interference” (between incoherent sources at A and B) Two monochromatic but incoherent sources (i. e. with random, time dependent phase) produce no interference pattern at the screen -assuming we time-average our measurement over many fluctuations r. A 1 A d P 1 r. B 1 (brackets again indicate time average) B L >> d Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 5

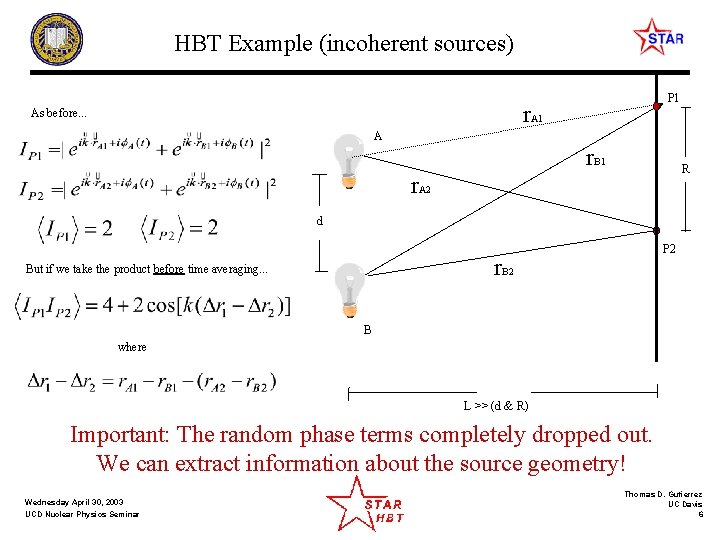
HBT Example (incoherent sources) P 1 r. A 1 As before. . . A r. B 1 R r. A 2 d P 2 r. B 2 But if we take the product before time averaging. . . B where L >> (d & R) Important: The random phase terms completely dropped out. We can extract information about the source geometry! Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 6

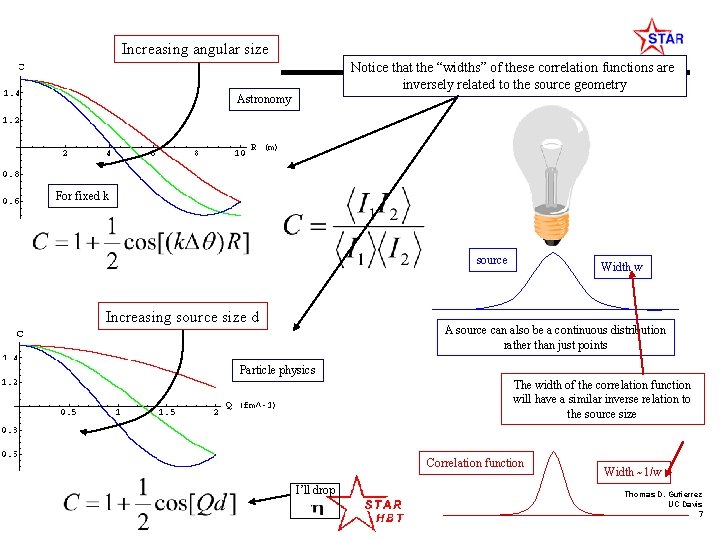
Increasing angular size Notice that the “widths” of these correlation functions are inversely related to the source geometry Astronomy For fixed k source Increasing source size d Width w A source can also be a continuous distribution rather than just points Particle physics The width of the correlation function will have a similar inverse relation to the source size Correlation function I’ll drop Wednesday April 30, 2003 UCD Nuclear Physics Seminar Width ~1/w Thomas D. Gutierrez UC Davis 7

More About HBT As we’ve seen, when treated with classical waves, HBT is basically just a kind of beat phenomenon When treated quantum mechanically (i. e. actually counting particles) the situation is more complex Lets define the two particle correlation function as: e density matrix in the second expression tells us two very important things C 2 is sensitive not only to the quantum statistics (determined by the commutation relations of the a and a’) but also the quantum field configuration; C 2 is sensitive to the source distribution, the dynamics of the problem, as well as any space-momentum correlations Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 8

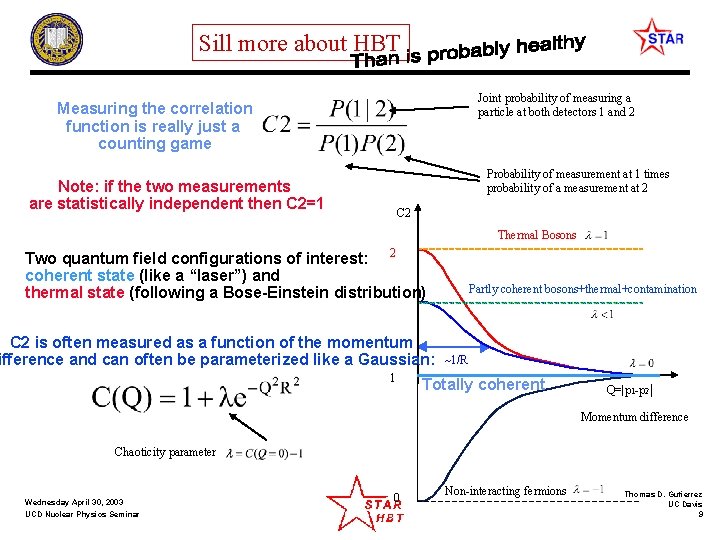
Sill more about HBT Joint probability of measuring a particle at both detectors 1 and 2 Measuring the correlation function is really just a counting game Probability of measurement at 1 times probability of a measurement at 2 Note: if the two measurements are statistically independent then C 2=1 C 2 Thermal Bosons Two quantum field configurations of interest: 2 coherent state (like a “laser”) and thermal state (following a Bose-Einstein distribution) C 2 is often measured as a function of the momentum ifference and can often be parameterized like a Gaussian: 1 Partly coherent bosons+thermal+contamination ~1/R Totally coherent Q=|p 1 -p 2| Momentum difference Chaoticity parameter Wednesday April 30, 2003 UCD Nuclear Physics Seminar 0 Non-interacting fermions Thomas D. Gutierrez UC Davis 9

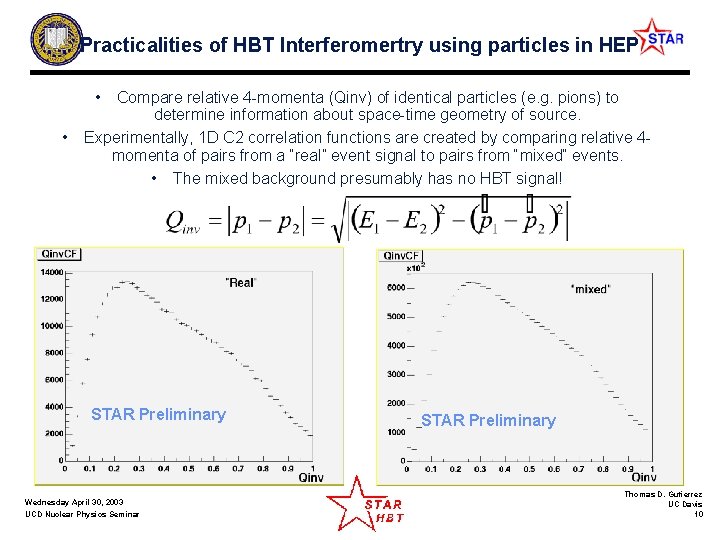
Practicalities of HBT Interferomertry using particles in HEP • Compare relative 4 -momenta (Qinv) of identical particles (e. g. pions) to determine information about space-time geometry of source. • Experimentally, 1 D C 2 correlation functions are created by comparing relative 4 momenta of pairs from a “real” event signal to pairs from “mixed” events. • The mixed background presumably has no HBT signal! STAR Preliminary Wednesday April 30, 2003 UCD Nuclear Physics Seminar STAR Preliminary Thomas D. Gutierrez UC Davis 10

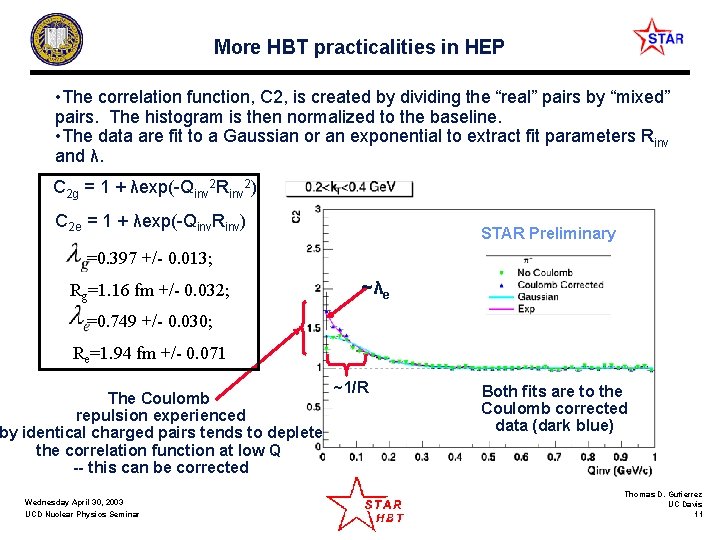
More HBT practicalities in HEP • The correlation function, C 2, is created by dividing the “real” pairs by “mixed” pairs. The histogram is then normalized to the baseline. • The data are fit to a Gaussian or an exponential to extract fit parameters Rinv and λ. C 2 g = 1 + λexp(-Qinv 2 Rinv 2) C 2 e = 1 + λexp(-Qinv. Rinv) STAR Preliminary =0. 397 +/- 0. 013; Rg=1. 16 fm +/- 0. 032; ~λe =0. 749 +/- 0. 030; Re=1. 94 fm +/- 0. 071 The Coulomb repulsion experienced by identical charged pairs tends to deplete the correlation function at low Q -- this can be corrected Wednesday April 30, 2003 UCD Nuclear Physics Seminar ~1/R Both fits are to the Coulomb corrected data (dark blue) Thomas D. Gutierrez UC Davis 11

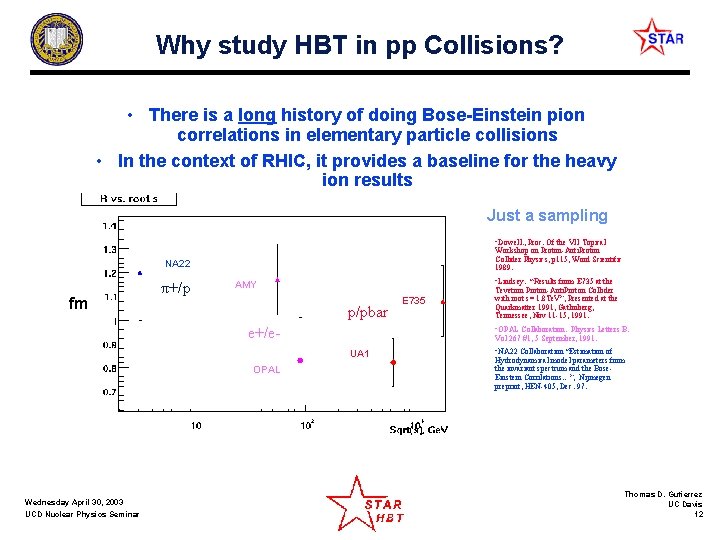
Why study HBT in pp Collisions? • There is a long history of doing Bose-Einstein pion correlations in elementary particle collisions • In the context of RHIC, it provides a baseline for the heavy ion results Just a sampling • Dowell. , Proc. Of the VII Topical Workshop on Proton-Anti. Proton Collider Physics, p 115, Word Scientific 1989. NA 22 fm π+/p • Lindsey. “Results from E 735 at the AMY p/pbar e+/e- Wednesday April 30, 2003 UCD Nuclear Physics Seminar Tevetron Proton-Anti. Proton Collider with root s= 1. 8 Te. V”, Presented at the Quarkmatter 1991, Gatlinberg, Tennessee, Nov 11 -15, 1991. • OPAL Collaboration. Physics Letters B. Vol 267 #1, 5 September, 1991. UA 1 OPAL E 735 • NA 22 Collaboration “Estimation of Hydrodynamical model parameters from the invariant spectrum and the Bose. Einstein Corrilations…”, Nijmegen preprint, HEN-405, Dec. 97. Thomas D. Gutierrez UC Davis 12

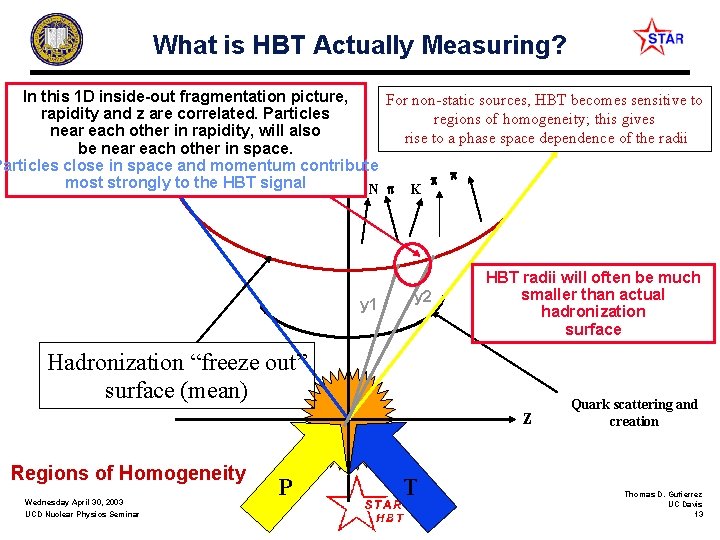
What is HBT Actually Measuring? In this 1 D inside-out fragmentation picture, For non-static sources, HBT becomes sensitive to t rapidity and z are correlated. Particles regions of homogeneity; this gives near each other in rapidity, will also rise to a phase space dependence of the radii be near each other in space. Particles close in space and momentum contribute most strongly to the HBT signal N K y 1 y 2 Hadronization “freeze out” surface (mean) Regions of Homogeneity Wednesday April 30, 2003 UCD Nuclear Physics Seminar P HBT radii will often be much smaller than actual hadronization surface z T Quark scattering and creation Thomas D. Gutierrez UC Davis 13

HBT Study of the pp System • HBT studies in pp interactions provide a peek into the fascinating softphysics regime of hadronic collisions • • • Some HBT-related questions: What do the regions of homogeneity look like? What is the pair source distribution function? How do the HBT parameters depend on event multiplicity? Do the HBT parameters depend on the polarization of the initial state (a fun idea but won’t have time to talk about it today)? This analysis is a first step in answering some of these questions Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 14

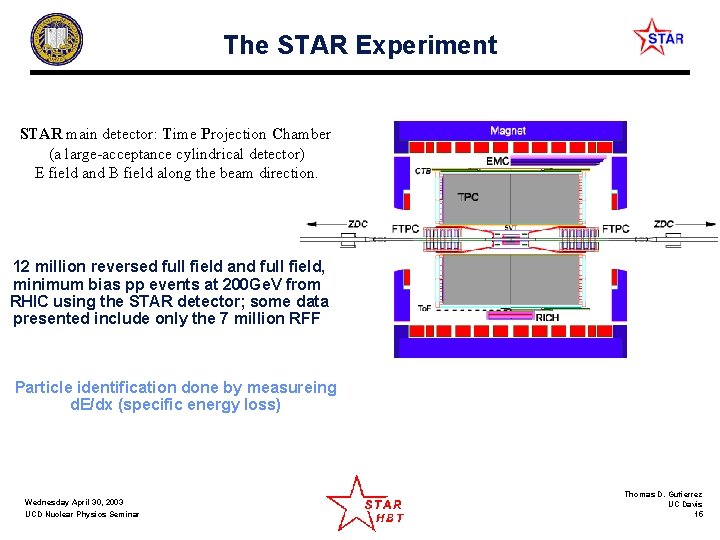
The STAR Experiment STAR main detector: Time Projection Chamber (a large-acceptance cylindrical detector) E field and B field along the beam direction. 12 million reversed full field and full field, minimum bias pp events at 200 Ge. V from RHIC using the STAR detector; some data presented include only the 7 million RFF Particle identification done by measureing d. E/dx (specific energy loss) Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 15

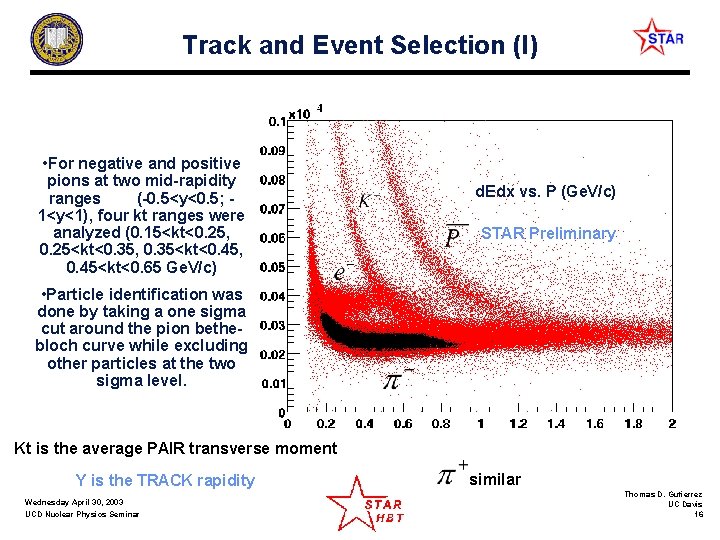
Track and Event Selection (I) • For negative and positive pions at two mid-rapidity ranges (-0. 5<y<0. 5; 1<y<1), four kt ranges were analyzed (0. 15<kt<0. 25, 0. 25<kt<0. 35, 0. 35<kt<0. 45, 0. 45<kt<0. 65 Ge. V/c) d. Edx vs. P (Ge. V/c) STAR Preliminary • Particle identification was done by taking a one sigma cut around the pion bethebloch curve while excluding other particles at the two sigma level. Kt is the average PAIR transverse moment Y is the TRACK rapidity Wednesday April 30, 2003 UCD Nuclear Physics Seminar similar Thomas D. Gutierrez UC Davis 16

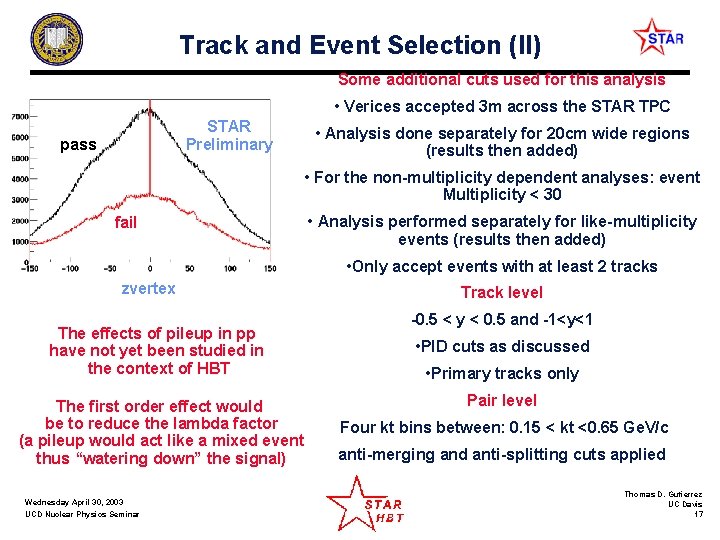
Track and Event Selection (II) Some additional cuts used for this analysis • Verices accepted 3 m across the STAR TPC STAR Preliminary pass • Analysis done separately for 20 cm wide regions (results then added) • For the non-multiplicity dependent analyses: event Multiplicity < 30 fail • Analysis performed separately for like-multiplicity events (results then added) • Only accept events with at least 2 tracks zvertex The effects of pileup in pp have not yet been studied in the context of HBT The first order effect would be to reduce the lambda factor (a pileup would act like a mixed event thus “watering down” the signal) Wednesday April 30, 2003 UCD Nuclear Physics Seminar Track level -0. 5 < y < 0. 5 and -1<y<1 • PID cuts as discussed • Primary tracks only Pair level Four kt bins between: 0. 15 < kt <0. 65 Ge. V/c anti-merging and anti-splitting cuts applied Thomas D. Gutierrez UC Davis 17

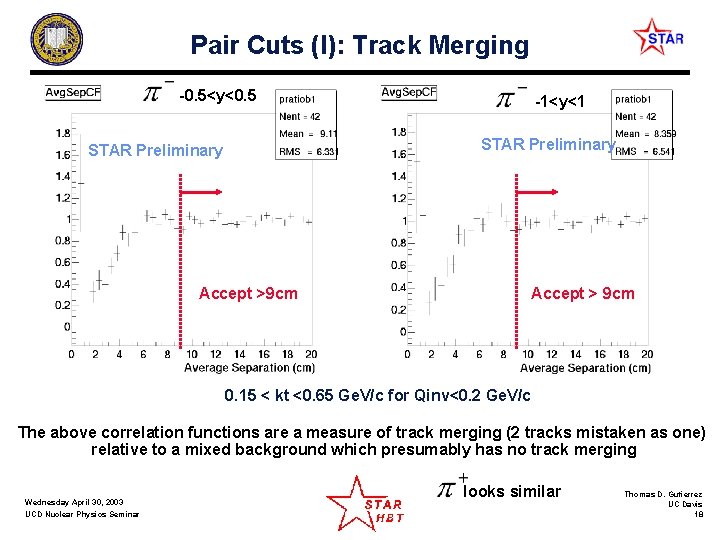
Pair Cuts (I): Track Merging -0. 5<y<0. 5 -1<y<1 STAR Preliminary Accept >9 cm Accept > 9 cm 0. 15 < kt <0. 65 Ge. V/c for Qinv<0. 2 Ge. V/c The above correlation functions are a measure of track merging (2 tracks mistaken as one) relative to a mixed background which presumably has no track merging Wednesday April 30, 2003 UCD Nuclear Physics Seminar looks similar Thomas D. Gutierrez UC Davis 18

Pair Cuts (II): Track Splitting -0. 5<y<0. 5 Splitting is when one track is mistaken as 2 STAR Preliminary Accept -0. 5<Quality<0. 6 Pads with two hits are circled Qual~0 no splitting (really DO have 2 tracks) Qual=1 totally split 0. 15 < kt <0. 65 Ge. V/c (one track mistaken as 2) The above correlation function is a measure of the quality relative to a mixed background. The mixed background presumably has no splitting (high quality means more splitting) Wednesday April 30, 2003 UCD Nuclear Physics Seminar and +/- 1 y looks similar Thomas D. Gutierrez UC Davis 19

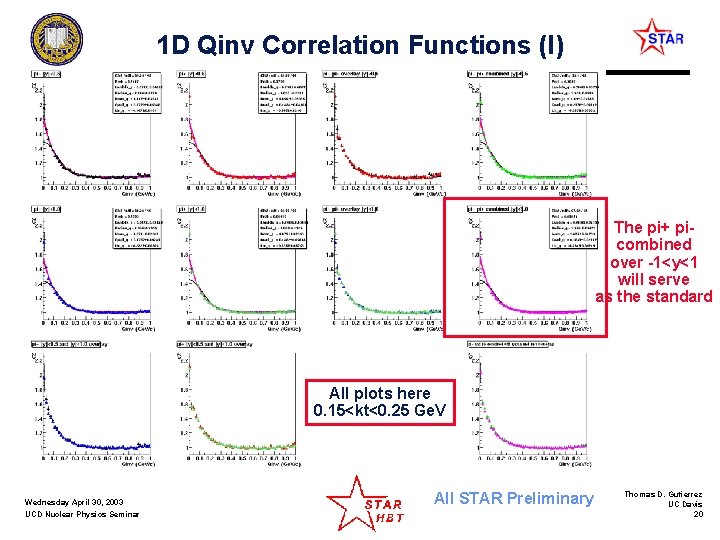
1 D Qinv Correlation Functions (I) All fits are to the Coulomb corrected data: The pi+ picombined over -1<y<1 will serve as the standard All plots here 0. 15<kt<0. 25 Ge. V Wednesday April 30, 2003 UCD Nuclear Physics Seminar All STAR Preliminary Thomas D. Gutierrez UC Davis 20

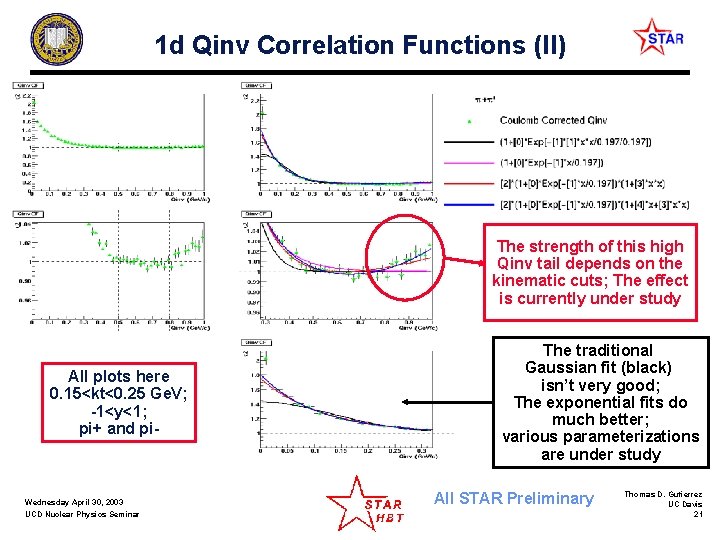
1 d Qinv Correlation Functions (II) The strength of this high Qinv tail depends on the kinematic cuts; The effect is currently under study All plots here 0. 15<kt<0. 25 Ge. V; -1<y<1; pi+ and pi- Wednesday April 30, 2003 UCD Nuclear Physics Seminar The traditional Gaussian fit (black) isn’t very good; The exponential fits do much better; various parameterizations are under study All STAR Preliminary Thomas D. Gutierrez UC Davis 21

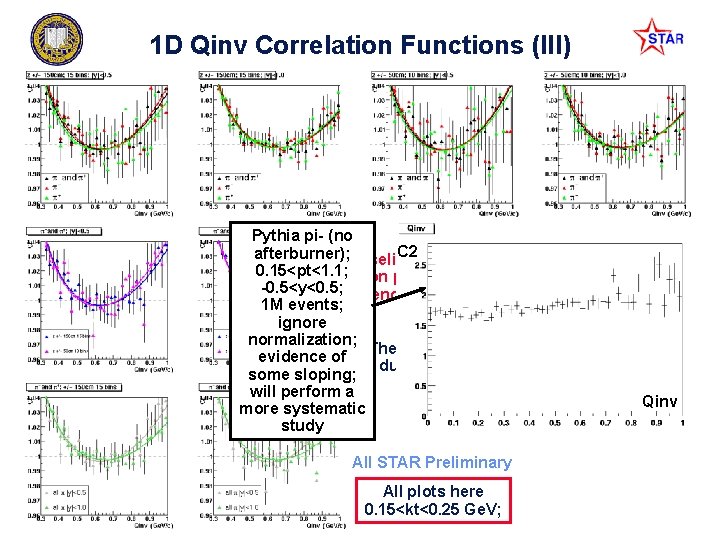
1 D Qinv Correlation Functions (III) Pythia pi- (no C 2 curvature depends only very weakly afterburner); Baseline 0. 15<pt<1. 1; on particle species and zvertex choices; -0. 5<y<0. 5; depends more strongly on rapidity and kt cuts; 1 M events; Still a rather small effect overall ignore normalization; The current hypothesis is that the effect evidence of is due to energy-momentum conservation some sloping; will perform a Qinv more systematic study All STAR Preliminary Wednesday April 30, 2003 UCD Nuclear Physics Seminar All plots here 0. 15<kt<0. 25 Ge. V; Thomas D. Gutierrez UC Davis 22

1 D Qinv HBT Parameters R (fm) All are from 0. 15<kt<0. 25 Ge. V; -1<y<1; pi+ and pi- Highly parameterization dependent values = bad Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 23

Source Image Another interesting way to approach HBT is one can transform the correlation function to obtain the actual source numerically Thermal limit: Koonin-Pratt equation S is the source distribution and represents the probability of emitting a pair of particles with relative 4 -momentum=Qinv separated by a distance r; S is the quantity we want to extract K 0 is the angle averaged integration kernel and is given by is the pair wavefunction and includes all the appropriate quantum statistics and relevant interactions between the pair Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 24

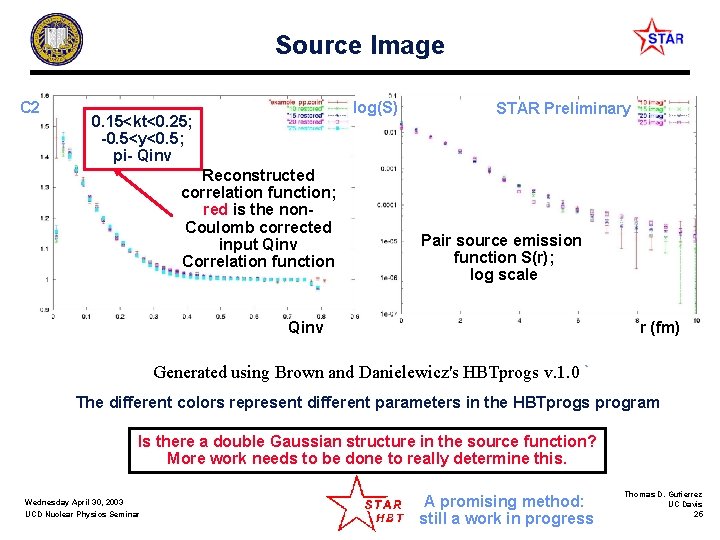
Source Image C 2 log(S) 0. 15<kt<0. 25; -0. 5<y<0. 5; pi- Qinv Reconstructed correlation function; red is the non. Coulomb corrected input Qinv Correlation function STAR Preliminary Pair source emission function S(r); log scale Qinv r (fm) Generated using Brown and Danielewicz's HBTprogs v. 1. 0 ` The different colors represent different parameters in the HBTprogs program Is there a double Gaussian structure in the source function? More work needs to be done to really determine this. Wednesday April 30, 2003 UCD Nuclear Physics Seminar A promising method: still a work in progress Thomas D. Gutierrez UC Davis 25

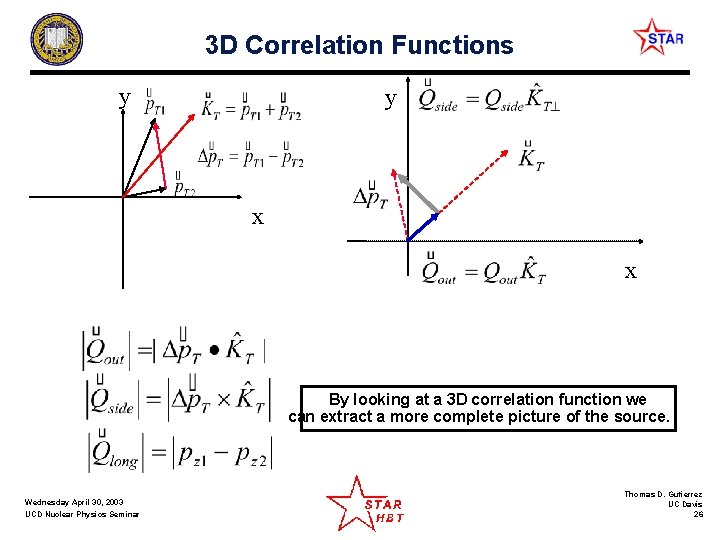
3 D Correlation Functions y y x x By looking at a 3 D correlation function we can extract a more complete picture of the source. Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 26

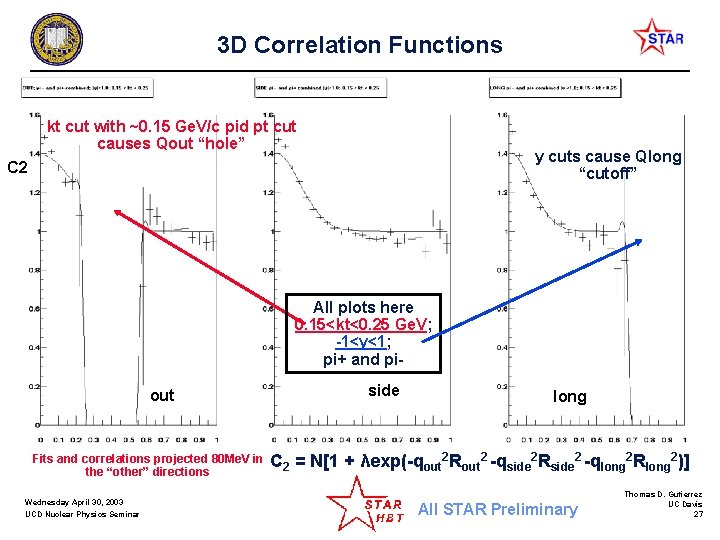
3 D Correlation Functions kt cut with ~0. 15 Ge. V/c pid pt cut causes Qout “hole” y cuts cause Qlong “cutoff” C 2 All plots here 0. 15<kt<0. 25 Ge. V; -1<y<1; pi+ and piout Fits and correlations projected 80 Me. V in the “other” directions Wednesday April 30, 2003 UCD Nuclear Physics Seminar side long C 2 = N[1 + λexp(-qout 2 Rout 2 -qside 2 Rside 2 -qlong 2 Rlong 2)] All STAR Preliminary Thomas D. Gutierrez UC Davis 27

3 D Correlation Parameters C 2 = N[1 + λexp(-qout 2 Rout 2 -qside 2 Rside 2 -qlong 2 Rlong 2)] Rout Rside 0. 15<kt<0. 25 Ge. V; -1<y<1; pi+ and pi- Rlong Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 28

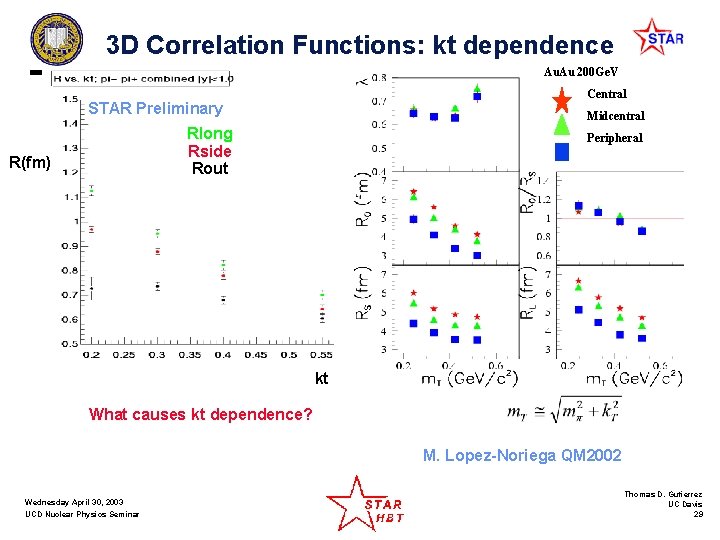
3 D Correlation Functions: kt dependence Au. Au 200 Ge. V Central STAR Preliminary Midcentral Rlong Rside Rout R(fm) Peripheral kt kt What causes kt dependence? M. Lopez-Noriega QM 2002 Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 29

What Causes Kt Dependence? Space momentum correlations We are looking at a region of homogeneity caused by: Space momentum correlations Kt = pair Pt Rout If the source is not static or collective effects are present Rsidethen space-momentum correlations can develop and cause the radii to change as you look in different locations in phase space. Some examples Inside-out fragmentation/ hadronization jets (the ultimate space-momentum correlation) fireball-like expansion Not all of these will give the collective flow same kt dependence. The rick is in distinguishing between them. This is currently under study Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 30

Multiplicity Dependence of HBT parameters It has been reported by some experiments (e. g. UA 1 ppbar at 630 Ge. V) that lambda tends to drop with event multiplicity while the radius increases slowly Other experiments (e. g. NA 27 pp at 27 Ge. V) report that lambda is flat as a function of event multiplicity This puzzle has numerous explanations from the mundane to the exotic. Some current speculations: Pion emission becomes more coherent in high multiplicity events involving particle-antiparticle collisions but not particle-particle High multiplicity events from ppbar may involve multistring fragmentation -- pions from different strings will not correlate strongly Resonance contributions and other contaminates may contribute to different degrees at different multiplicities at different experiments All of the above would have the tendency to reduce lambda Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 31

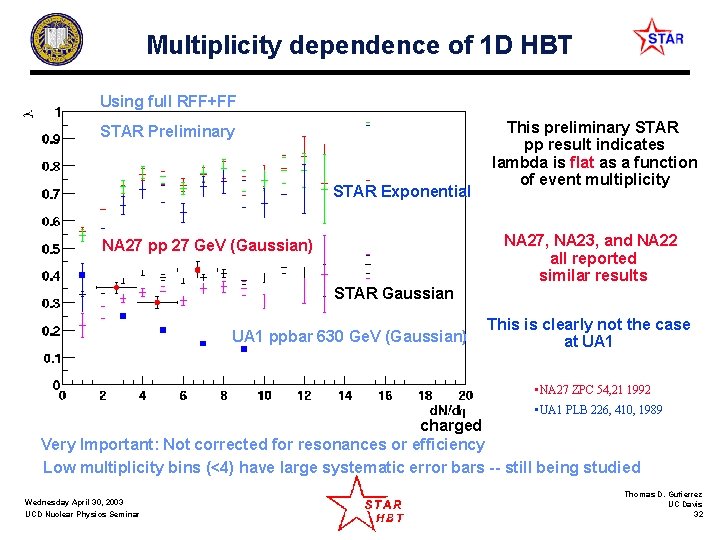
Multiplicity dependence of 1 D HBT Using full RFF+FF STAR Preliminary STAR Exponential This preliminary STAR pp result indicates lambda is flat as a function of event multiplicity NA 27, NA 23, and NA 22 all reported similar results NA 27 pp 27 Ge. V (Gaussian) STAR Gaussian UA 1 ppbar 630 Ge. V (Gaussian) This is clearly not the case at UA 1 • NA 27 ZPC 54, 21 1992 • UA 1 PLB 226, 410, 1989 charged Very Important: Not corrected for resonances or efficiency Low multiplicity bins (<4) have large systematic error bars -- still being studied Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 32

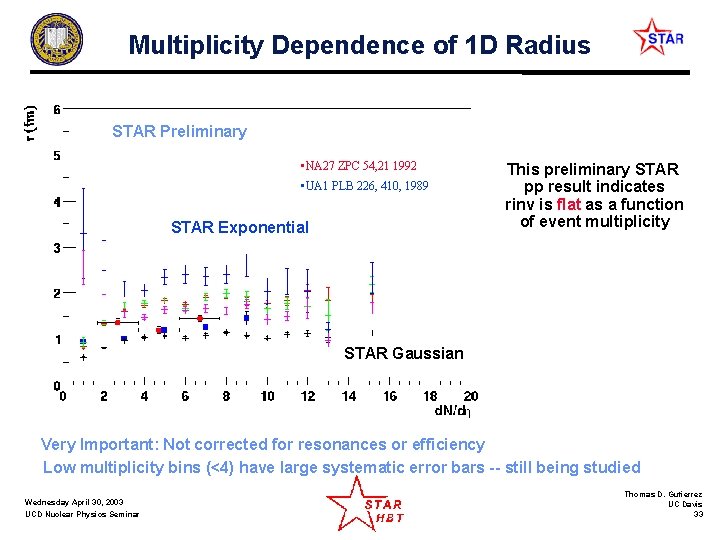
Multiplicity Dependence of 1 D Radius STAR Preliminary • NA 27 ZPC 54, 21 1992 • UA 1 PLB 226, 410, 1989 STAR Exponential This preliminary STAR pp result indicates rinv is flat as a function of event multiplicity STAR Gaussian Very Important: Not corrected for resonances or efficiency Low multiplicity bins (<4) have large systematic error bars -- still being studied Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 33

Summary Bose-Einstein correlations provide a means of probing the space-time geometry of the pion emission source in high energy collisions; The pion emission source size is ~1 fm A kt dependence is seen in the 3 D HBT parameters of pp collisions indicating a pion source with space-momentum correlations; The nature of ths source is still under study Lambda and rinv are constant as a function of event multiplicity; This is consistent with other pp experiments but differ from ppbar results; The effect is still under study Wednesday April 30, 2003 UCD Nuclear Physics Seminar Thomas D. Gutierrez UC Davis 34