Bootstrap Confidence Intervals for Threeway Component Methods Henk

Bootstrap Confidence Intervals for Three-way Component Methods Henk A. L. Kiers University of Groningen The Netherlands 1

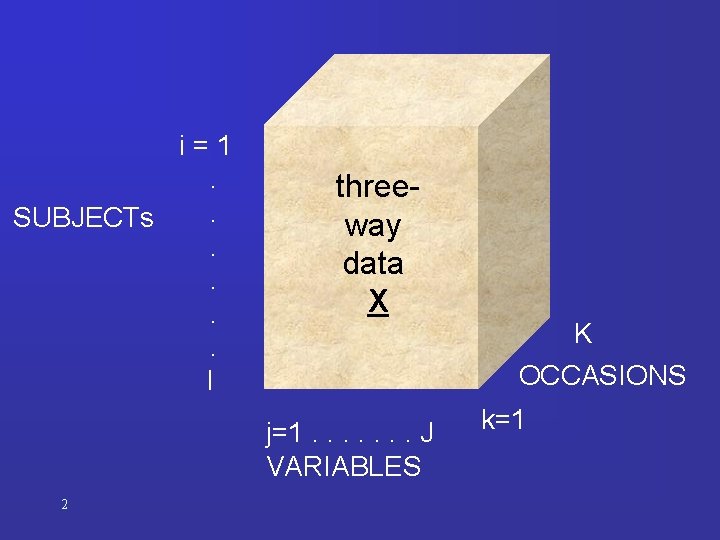
i=1. . SUBJECTs. . I threeway data X j=1. . . . J VARIABLES 2 K OCCASIONS k=1

i=1. SUBJECTs. . . threeway data X K OCCASIONS j=1. . . . J k=1 VARIABLES Three-way Methods: I Tucker 3 Xa = AGa(C B ) + Ea A (I P), B (J Q), C (K R) component matrices Ga matricized version of G (P Q R) core array CP = Candecomp/Parafac Xa = AGa(C B ) + Ea G (R R R) superdiagonal Practice: • three-way methods applied to sample from population 3 • goal: results should pertain to population

Example (Kiers & Van Mechelen 2001): • scores of 140 individuals, on 14 anxiousness response scales in 11 different situations • Tucker 3 with P=6, Q=4, R=3 (41. 1%) Rotation: B, C, and Core to simple structure 4

Results for example data Kiers & Van Mechelen 2001: B 5

C 6

Core 7

Is solutions stable? Is solution ‘reliable’? Would it also hold for population? Kiers & Van Mechelen report split-half stability results: Split-half results: rather global stability measures 8

How can we assess degree of stability/reliability of individual results? confidence intervals (CI) for all parameters • not readily available • derivable under rather strong assumptions (e. g. , normal distributions, full identification) • alternative: BOOTSTRAP 9

BOOTSTRAP • distribution free • very flexible (CI’s for ‘everything’) • can deal with nonunique solutions • computationally intensive 10

Bootstrap procedure: Analyze sample data X (I J K) by desired method sample outcomes (e. g. , A, B, C and G) Repeat for b=1: 500 • draw sample with replacement from I slabs of X Xb (I J K) • analyze bootstrap sample Xb in same way as sample outcomes b (e. g. , Ab, Bb, Cb and Gb) For each individual parameter : • 500 values available • range of 95% middle values 11 “ 95% percentile interval” ( Confidence Interval)

Basic idea of bootstrap: • distribution in sample = nonparametric maximum likelihood estimate of population distribution • draw samples from estimated population distribution, just as actual sample drawn from population From which mode do we resample? Answer: mimic how we sampled from population • sample subjects from population resample A-mode 12

Three questions: • How deal with transformational nonuniqueness? Lots of possibilities, depends on interpretation • Are bootstrap intervals good approximations of confidence intervals? Not too bad • How deal with computational problems (if any)? Simple effective procedure 13

1. How to deal with transformational nonuniqueness? • identify solution completely • identify solution up to permutation/reflection for CP and Tucker 3 • identify solution up to orthogonal transformations • identify solution up to arbitrary nonsingular transformations only for Tucker 3 14

Identify solution completely: uniquely defined outcome parameters bootstrap straightforward (CI’s directly available) CP and Tucker 3 (principal axes or simple structure) - solution identified up to scaling/permutation Both cases: - further identification needed 15

Identify solution up to permutation/reflection outcome parameters b may differ much, but maybe only due to ordering or sign bootstrap CI’s unrealistically broad ! how to make b’s comparable? Solution: reorder and reflect columns in (e. g. ) Bb, Cb such that Bb, Cb optimally resemble B, C 16 does not affect fit

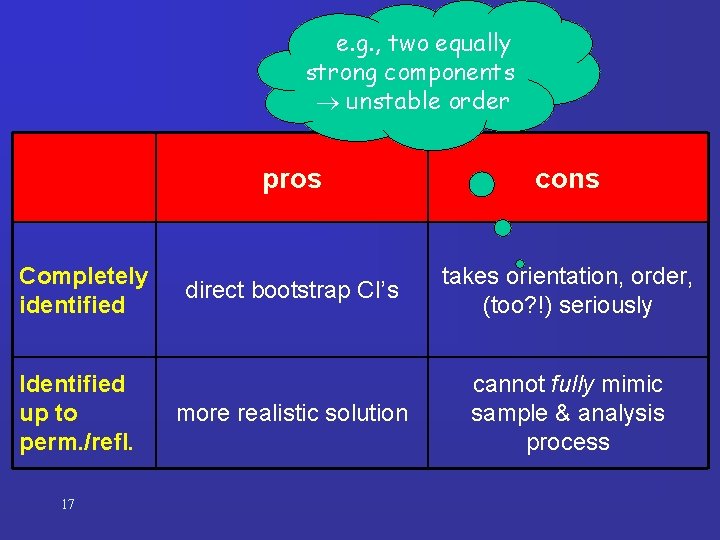
e. g. , two equally strong components unstable order Completely identified Identified up to perm. /refl. 17 pros cons direct bootstrap CI’s takes orientation, order, (too? !) seriously more realistic solution cannot fully mimic sample & analysis process

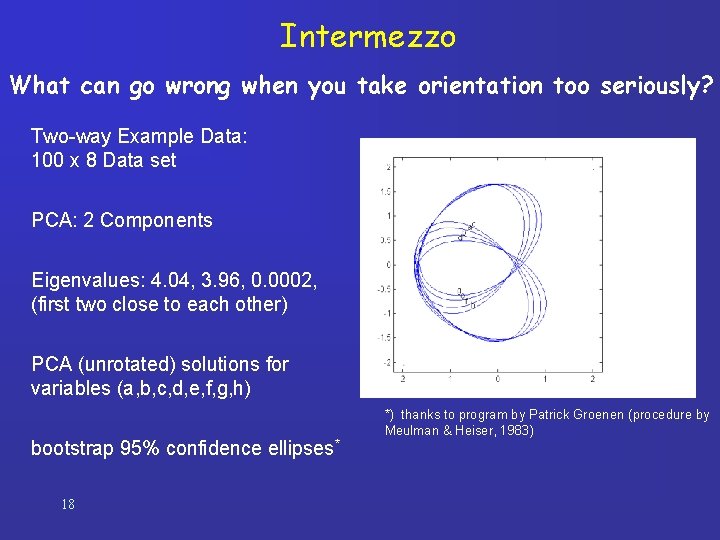
Intermezzo What can go wrong when you take orientation too seriously? Two-way Example Data: 100 x 8 Data set PCA: 2 Components Eigenvalues: 4. 04, 3. 96, 0. 0002, (first two close to each other) PCA (unrotated) solutions for variables (a, b, c, d, e, f, g, h) bootstrap 95% confidence ellipses* 18 *) thanks to program by Patrick Groenen (procedure by Meulman & Heiser, 1983)

What caused these enormous ellipses? Look at loadings for data and some bootstraps: … leading to standard errors: . . . 19

Conclusion: solutions very unstable, hence: loadings seem very uncertain However …. Configurations of subsamples very similar So: We should’ve considered the whole configuration ! 20

Identify solution up to orthogonal transformations Tucker 3 solution with A, B, C columnwise orthonormal: any rotation gives same fit (counterrotation of core) outcome parameters b may differ much, but maybe only due to coincidental ‘orientation’ bootstrap CI’s unrealistically broad Make b’s comparable: rotate Bb, Cb, Gb such that they optimally resemble B, C, G comparable across bootstraps How? • minimize f 1(T)=||Bb. T–B||2 and f 2(U)=||Cb. U–C||2 • counterrotate core: Gb(U T) • minimize f 3(S)=||SGb–G||2 • use Bb* = Bb. T , Cb* = Cb. U, Gb* = SGb to determine 95%CI’s 21

Notes: • first choose orientation of sample solution (e. g. , principal axes or other) • order of rotations (first B and C, then G): somewhat arbitrary, but may have effect 22

Identify solution up to nonsingular transformations. . analogously. . . transform Bb, Cb, Gb so as to optimally resemble B, C, G 23

Expectation: the more transformational freedom used in bootstraps the smaller the CI’s Example: • anxiety data set (140 subjects, 14 scales, 11 situations) • apply 4 bootstrap procedures • compare bootstrap se’s of all outcomes 24

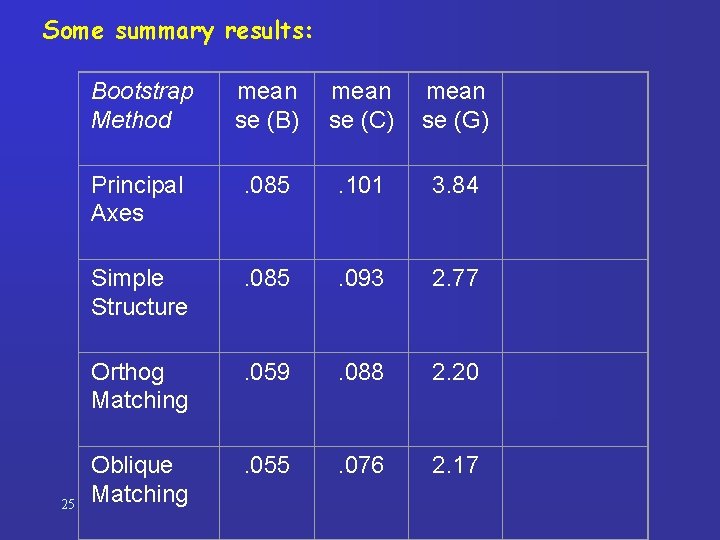
Some summary results: 25 Bootstrap Method mean se (B) mean se (C) mean se (G) Principal Axes . 085 . 101 3. 84 Simple Structure . 085 . 093 2. 77 Orthog Matching . 059 . 088 2. 20 Oblique Matching . 055 . 076 2. 17

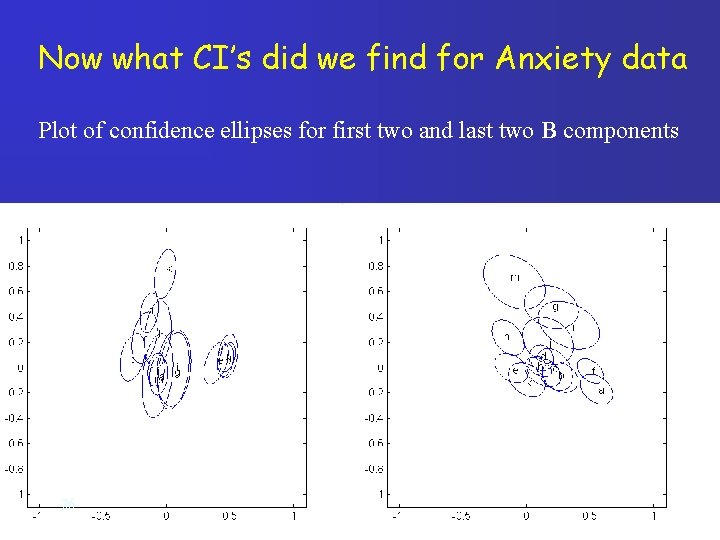
Now what CI’s did we find for Anxiety data Plot of confidence ellipses for first two and last two B components 26

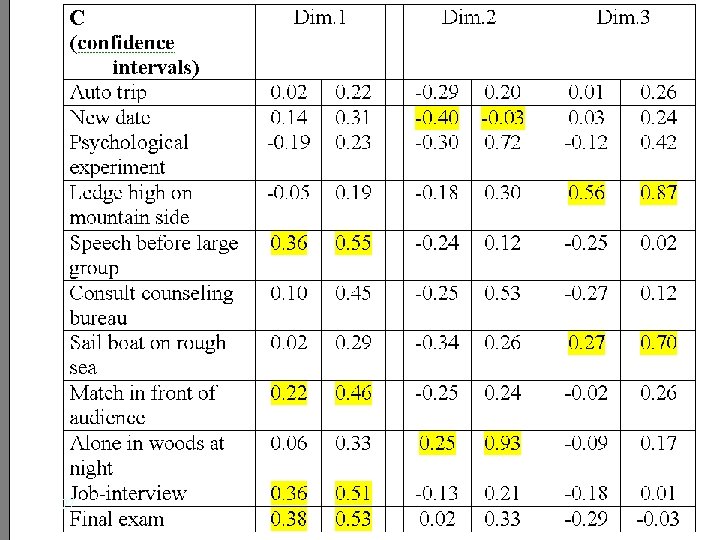
Confidence intervals for Situation Loadings 27

Confidence intervals for Higest Core Values 28

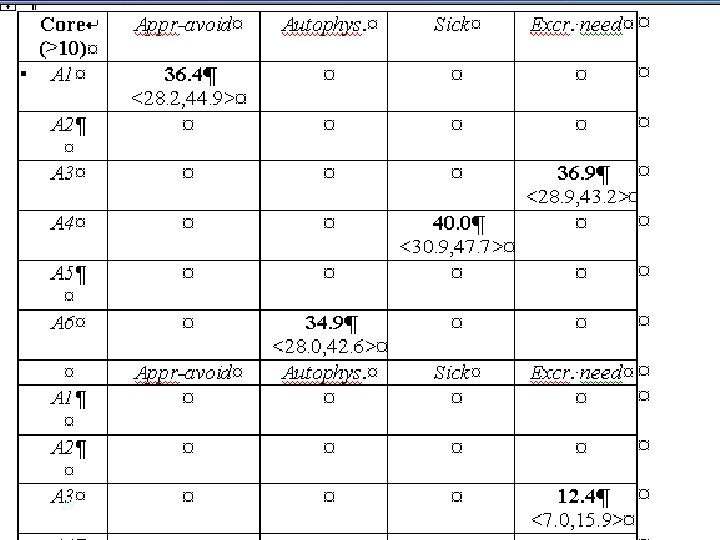
29

2. Are bootstrap intervals good approximations of Confidence Intervals? 95%CI should contain popul. values in 95% of samples “coverage” should be 95% Answered by SIMULATION STUDY Set up: • construct population with Tucker 3/CP structure + noise • apply Tucker 3/CP to population parameters • draw samples from population • apply Tucker 3/CP to sample and construct bootstrap CI’s • check coverage: how many CI’s contain popul. parameter 30

Design of simulation study: • noise: low, medium, high • sample size (I): 20, 50, 100 • 6 size conditions: (J=4, 8, K=6, 20, core: 222, 333, 432) Other Choices • number of bootstraps: always 500 • number of populations: 10 • number of samples 10 Each cell: 10 10 500 = 50000 Tucker 3 or CP analyses (full design: 3 3 6=54 conditions) 31

Should be close to 95% Here are the results 32

Some details: ranges of values per cell in design (and associated se’s) e g a r e v o s c n o w i o t l i d y l n l o a c e r n i s l e e s c a c e m c i o t a • S m e l ) b 0 o r 2 p = I t ( s • Mo small I with 33

3. How deal with computational problems (if any) Is there a problem? Computation times per 500 boostraps: (Note: largest data size: 100 8 20) CP: Tucker 3 (Simp. Str): Tucker 3 (Orthog. Match): Problem most severe with CP 34 min 4 s, max 452 s min 3 s, max 30 s min 1 s, max 23 s

How deal with computational problems for CP? Idea: Start bootstraps from sample solution Problem: May detract from coverage Tested by simulation: • CP with 5 different starts per bootstrap vs • Fast bootstrap procedure 35

Results: Fast method about 6 times faster (as expected) Coverage Optimal method: B: 95. 5% C: 95. 1% Fast method: B: 95. 3% C: 94. 7% • Time gain enormous • 36 Coverage hardly different

Conclusion & Discussion • Bootstrap CI’s seem reasonable • Matching makes intervals smaller • Computation times for Tucker 3 acceptable, for CP can be decreased by starting each bootstrap in sample solution 37

Conclusion & some first tests show that this Discussion works • What do bootstrap CI’s mean in case of matching? • 95% confidence for each value ? - chance capitalization - ignores dependence of parameters (they vary together) some first tests Show dependence by bootstrap movie. . . !? ! show that this does not work Develop joint intervals (hyperspheres). . . ? • Sampling from two modes (e. g. , A and C) ? 38