Boolean Algebra Sungho Kang Yonsei University Outline l

Boolean Algebra Sungho Kang Yonsei University

Outline l l l Set, Relations, and Functions Partial Orders Boolean Functions Don’t Care Conditions Incomplete Specifications Computer Systems Lab. YONSEI UNIVERSITY 2

Set Notation Set and Relations Element is a member of set Element is not a member of set Cardinality (number of members) of set Set is a subset of The empty set (a member of all sets) The complement of set The universe: Computer Systems Lab. YONSEI UNIVERSITY 3

Set Notation l l l Set and Relations Inclusion ( ) Proper Inclusion ( ) Complementation Intersection ( ) Union ( ) Difference Computer Systems Lab. YONSEI UNIVERSITY 4

Power Sets Set and Relations The power set of set (the set of all subsets of set The cardinality of a power set is a power of 2 Computer Systems Lab. YONSEI UNIVERSITY 5

Power Sets Set and Relations 3 -member set 1 subset with 0 members 3 subsets with 1 members 3 subsets with 2 members 1 subset with 3 members Power sets are Boolean Algebras Computer Systems Lab. YONSEI UNIVERSITY 6

Cartesian Products Set and Relations The Cartesian Product of sets A and B is denoted A x. B Suppose , then Set is unordered ( ) denotes Ordered Set Computer Systems Lab. YONSEI UNIVERSITY 7

Binary Relations l l Set and Relations The Cartesian Product of sets A and B is denoted A x B consists of all possible ordered pairs (a, b) such that and A subset is called a Binary Relation Graphs, Matrices, and Boolean Algebras can be viewed as binary relations Computer Systems Lab. YONSEI UNIVERSITY 8

Binary Relations as Graphs or Matrices a c b d f Bipartite Graph Computer Systems Lab. b a 1 c 1 d 0 1 Set and Relations f 0 1 Rectangular Matrix YONSEI UNIVERSITY 9
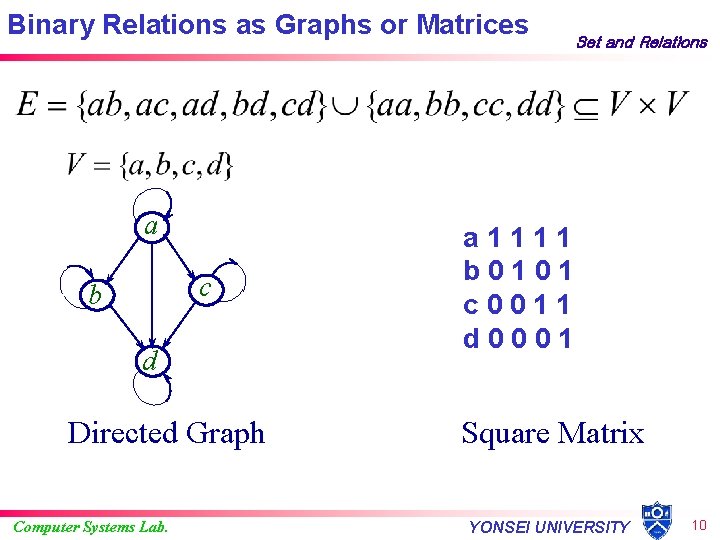
Binary Relations as Graphs or Matrices a c b d Directed Graph Computer Systems Lab. Set and Relations a 1111 b 0101 c 0011 d 0001 Square Matrix YONSEI UNIVERSITY 10

Properties of Binary Relations l l Set and Relations A binary relation can be § reflexive, and/or § transitive, and/or § symmetric, and/or § antisymmetric We illustrate these properties on the next few slides Computer Systems Lab. YONSEI UNIVERSITY 11

Notation for Binary Relations If , we say that of the relation , and that Set and Relations is the domain is the range. If , we say that the pair is in the relation , or. Computer Systems Lab. YONSEI UNIVERSITY 12

Missing Figure 3. 2, Page 80 3. 1. 3 Computer Systems Lab. Set and Relations YONSEI UNIVERSITY 13

Example: “Less than or Equal” Computer Systems Lab. Set and Relations YONSEI UNIVERSITY 14

Example: “a times b = 12” Computer Systems Lab. Set and Relations 1 2 3 12 6 4 YONSEI UNIVERSITY 15
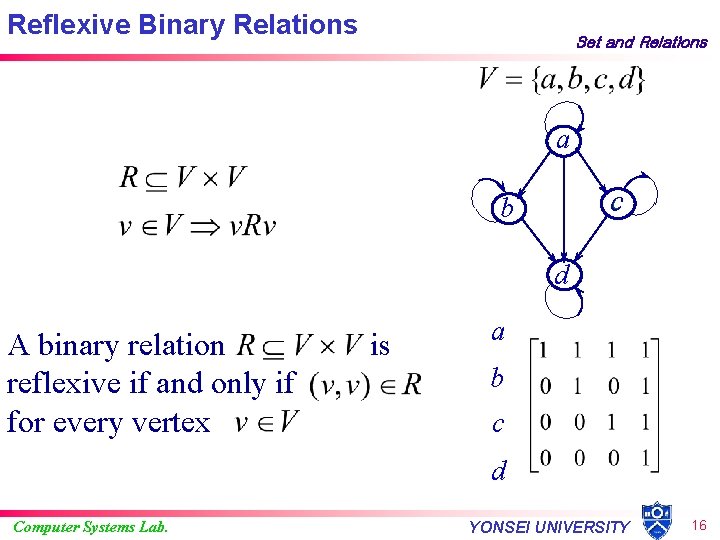
Reflexive Binary Relations Set and Relations a c b d A binary relation reflexive if and only if for every vertex is a b c d Computer Systems Lab. YONSEI UNIVERSITY 16
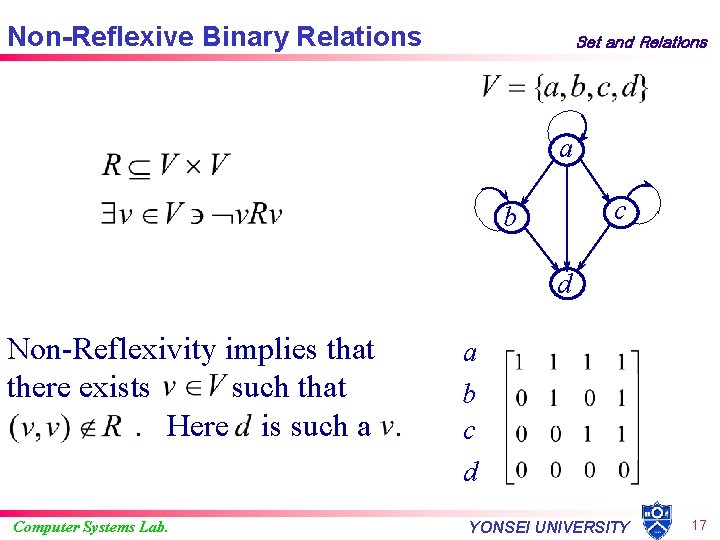
Non-Reflexive Binary Relations Set and Relations a c b d Non-Reflexivity implies that there exists such that. Here is such a. Computer Systems Lab. a b c d YONSEI UNIVERSITY 17
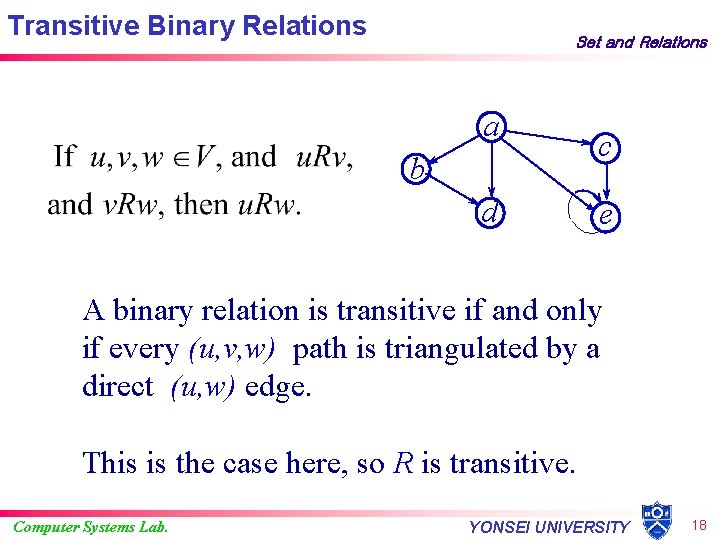
Transitive Binary Relations Set and Relations a b d c e A binary relation is transitive if and only if every (u, v, w) path is triangulated by a direct (u, w) edge. This is the case here, so R is transitive. Computer Systems Lab. YONSEI UNIVERSITY 18
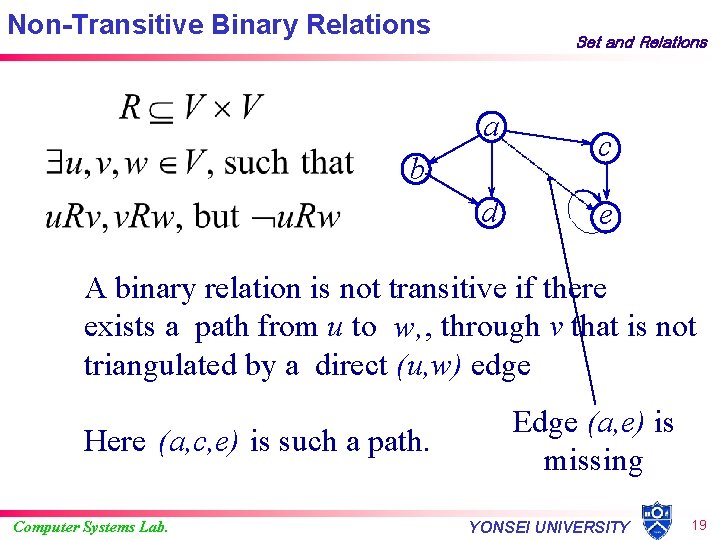
Non-Transitive Binary Relations Set and Relations a b d c e A binary relation is not transitive if there exists a path from u to w, , through v that is not triangulated by a direct (u, w) edge Here (a, c, e) is such a path. Computer Systems Lab. Edge (a, e) is missing YONSEI UNIVERSITY 19
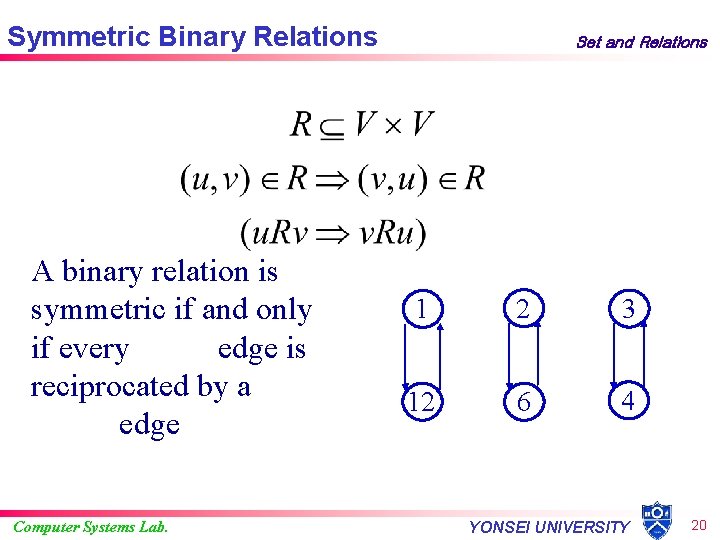
Symmetric Binary Relations A binary relation is symmetric if and only if every edge is reciprocated by a edge Computer Systems Lab. Set and Relations 1 2 3 12 6 4 YONSEI UNIVERSITY 20
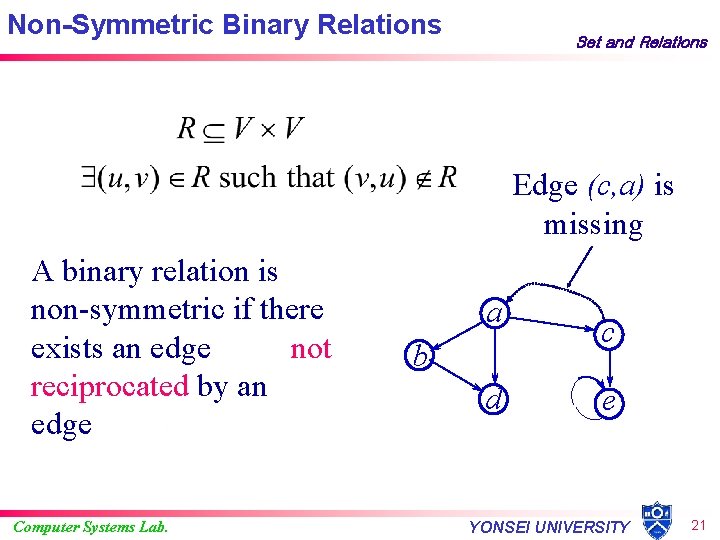
Non-Symmetric Binary Relations Set and Relations Edge (c, a) is missing A binary relation is non-symmetric if there exists an edge not reciprocated by an edge Computer Systems Lab. a b d c e YONSEI UNIVERSITY 21

Antisymmetric Binary Relations A binary relation is antisymmetric if and only if no edge is reciprocated by a edge Set and Relations a b d c e Not antisymmetric if any such edge is reciprocated : here Computer Systems Lab. YONSEI UNIVERSITY 22

Functions l l l Set and Relations A function f are binary relations from set A (called the domain) to B (called the range) But, it is required that each a in A be associated with exactly 1 b in B For functions, it cannot be true that both (a, b) in R and (a, c) in R, b different from c Computer Systems Lab. YONSEI UNIVERSITY 23
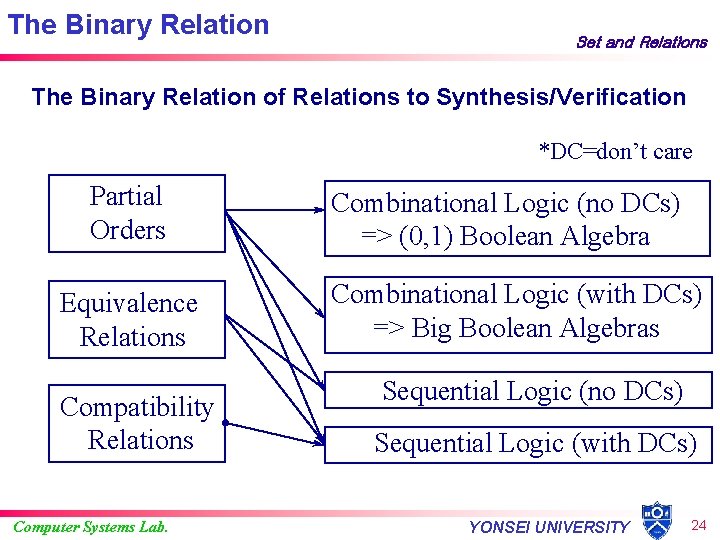
The Binary Relation Set and Relations The Binary Relation of Relations to Synthesis/Verification *DC=don’t care Partial Orders Equivalence Relations Compatibility Relations Computer Systems Lab. Combinational Logic (no DCs) => (0, 1) Boolean Algebra Combinational Logic (with DCs) => Big Boolean Algebras Sequential Logic (no DCs) Sequential Logic (with DCs) YONSEI UNIVERSITY 24
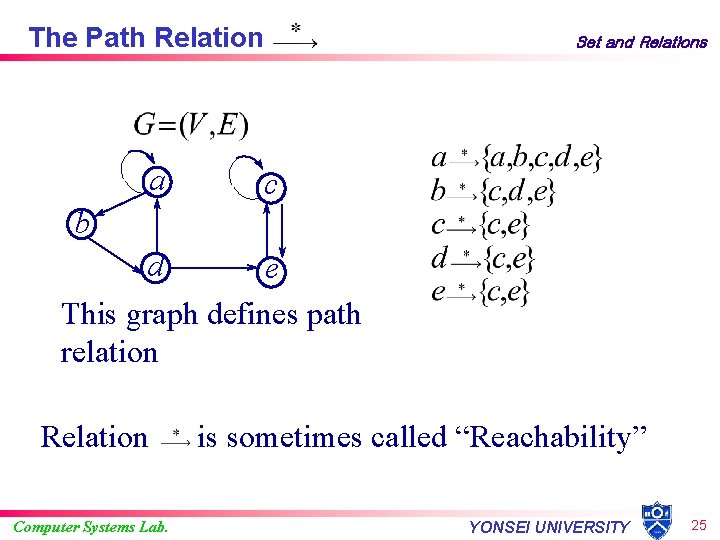
The Path Relation a Set and Relations c b d e This graph defines path relation Relation Computer Systems Lab. is sometimes called “Reachability” YONSEI UNIVERSITY 25
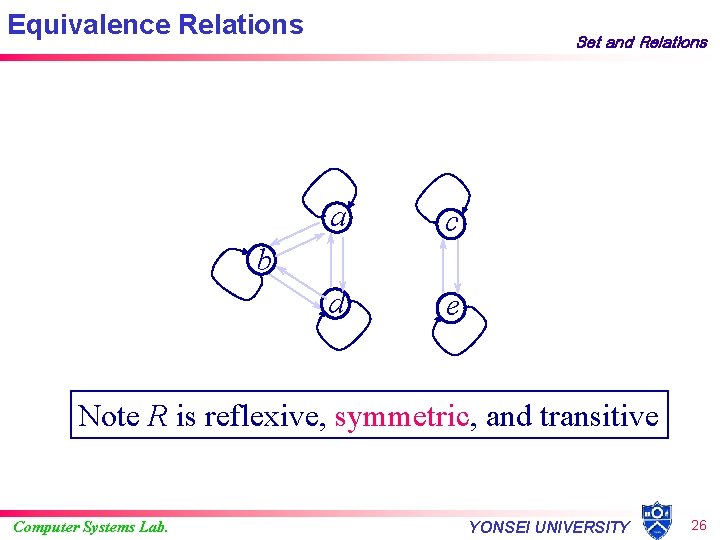
Equivalence Relations Set and Relations a c d e b Note R is reflexive, symmetric, and transitive Computer Systems Lab. YONSEI UNIVERSITY 26
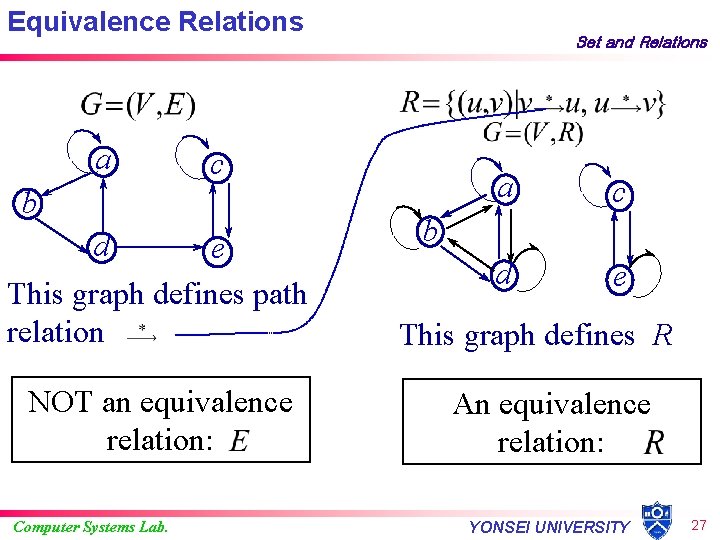
Equivalence Relations a c b d e This graph defines path relation NOT an equivalence relation: Computer Systems Lab. Set and Relations a c d e b This graph defines R An equivalence relation: YONSEI UNIVERSITY 27
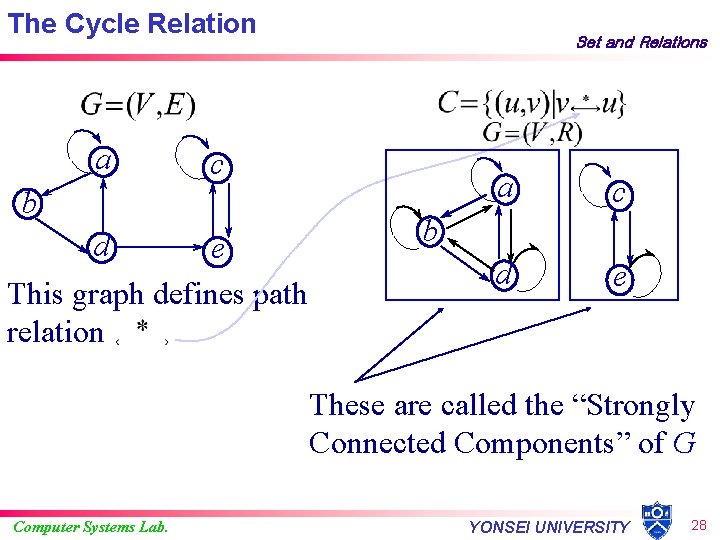
The Cycle Relation a Set and Relations c b d e This graph defines path relation a c d e b These are called the “Strongly Connected Components” of G Computer Systems Lab. YONSEI UNIVERSITY 28

Refinement l Set and Relations Given any set B a partition of B is a set of subsets Bi B with two properties § Bi Bj = for all i j § i B i = B l Given two partitions P 1 and P 2 of a set S, P 1 is a refinement of P 2 if each block B 1 i of P 1 is a subset of some block of 2 Computer Systems Lab. YONSEI UNIVERSITY 29

Other Binary Relations Set and Relations • Partial Orders (Includes Lattices, Boolean Algebras) • Reflexive • Transitive • Antisymmetric • Compatibility Relations • Reflexive • Not Transitive--Almost an equivalence relation • Symmetric Computer Systems Lab. YONSEI UNIVERSITY 30

Functions l Set and Relations A function f from A to B written f : A B is a rule that associates exactly one element of B to each element of A § A relation from A to B is a function if it is right-unique and if every element of A appears in one pair of the relation § A is called the domain of the function § B is called the co-domain (range) l If y=f(x) : A B, y is image of x § Given a domain subset C A IMG(f, C) = { y B | x C y = f(x) } § preimage of C under f PRE(f, C) = { x A | y C y = f(x) } l l A function f is one-to-one (injective) if x y implies f(x) f(y) A function f is onto (surjective) if for every y B, there exists an element x A, such that f(x) = y Computer Systems Lab. YONSEI UNIVERSITY 31

Algebraic Systems l l Partial Orders The pair is called an algebraic system is a set, called the carrier of the system is a relation on ( , are similar to ) This algebraic system is called a partially ordered set, or poset for short Computer Systems Lab. YONSEI UNIVERSITY 32

Partially Ordered Sets l l A poset has two operations, and meet and join (like AND and OR) Sometimes written or even , since is implied Computer Systems Lab. Partial Orders , called YONSEI UNIVERSITY 33
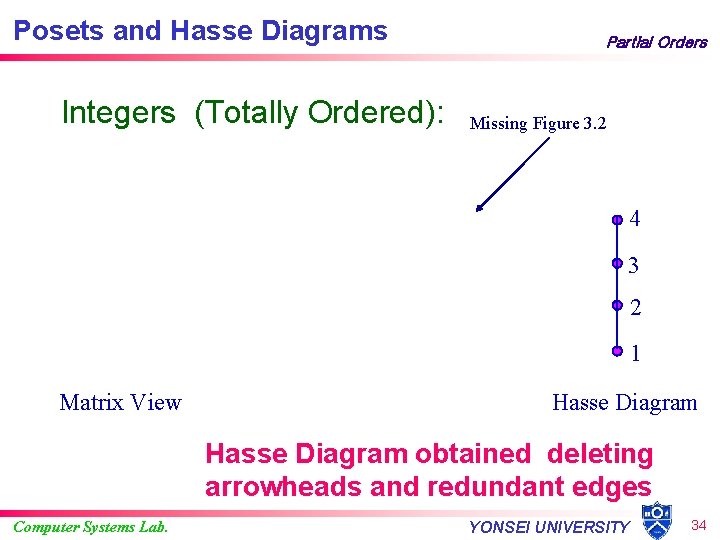
Posets and Hasse Diagrams Integers (Totally Ordered): Partial Orders Missing Figure 3. 2 4 3 2 1 Matrix View Hasse Diagram obtained deleting arrowheads and redundant edges Computer Systems Lab. YONSEI UNIVERSITY 34
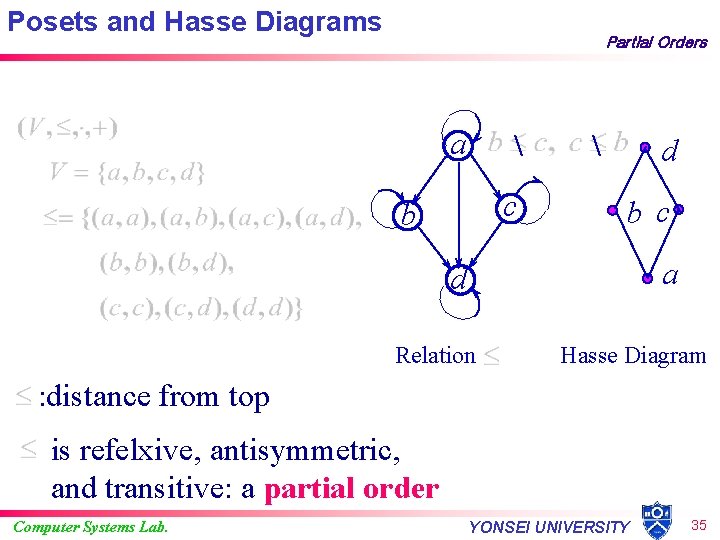
Posets and Hasse Diagrams Partial Orders a c b d b c a d Relation Hasse Diagram : distance from top is refelxive, antisymmetric, and transitive: a partial order Computer Systems Lab. YONSEI UNIVERSITY 35

Meet Partial Orders An element m of a poset P is a lower bound of elements a and b of P, if and. m is the greatest lower bound or meet of elements a and b if m is a lower bound of a and b and, for any such that and also , . Computer Systems Lab. YONSEI UNIVERSITY 36

Join: the Dual of Meet Partial Orders An element of a poset is a upper bound of elements and of , if and. is the least upper bound or join of elements if is an upper bound of and, for any that and also , . Computer Systems Lab. and such YONSEI UNIVERSITY 37
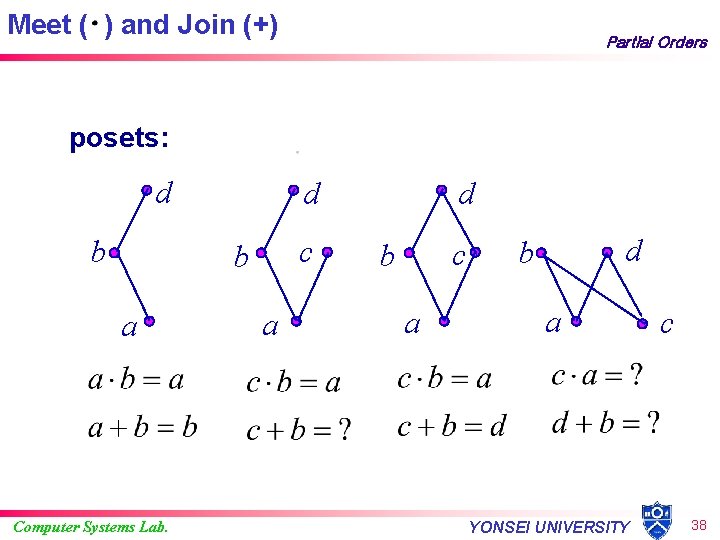
Meet ( ) and Join (+) Partial Orders posets: d b d c b a Computer Systems Lab. a d c b a d b a YONSEI UNIVERSITY c 38

POSET Properties Theorem 3. 2. 1 If and lower bound (meet), then Partial Orders have a greatest Similarly, if and have a least upper bound (join), then Proof: Since meet exists, Also, since join exists, Computer Systems Lab. by definition. YONSEI UNIVERSITY 39

More POSET Properties Partial Orders Theorem 3. 2. 2 Proof ( ): This means assume. • is a lower bound of and (by Def. ) • is also the meet of and Proof: by contradiction. Suppose. Then where. But since was a lower bound of and , as well. Thus , by the anti-symmetry of posets. Proof ( Computer Systems Lab. ): From Definition of meet YONSEI UNIVERSITY 40

Well-Ordered l l Partial Orders If all pairs of elements of a poset are comparable, then the set is totally ordered If every non-empty subset of a totally ordered set has a smallest element, then the set is well-ordered § e. g. ) Natural numbers l Mathematical Induction § Given, for all n N, propositions P(n), if ÄP(0) is true Äfor all n>0, if P(n-1) is true then P(n) is true § then, for all n N, P(n) is true Computer Systems Lab. YONSEI UNIVERSITY 41

Lattices l l l Partial Orders Lattice: a poset with both meet and join for every pair of elements of the carrier set Boolean Algebra: a distributed and complemented lattice Every lattice has a unique minimum element and a unique maximum element Computer Systems Lab. YONSEI UNIVERSITY 42

Lattices and Not Lattices d b d c b a (lattice) Partial Orders a d d b c b a a c (lattice) (Boolean algebra) Computer Systems Lab. YONSEI UNIVERSITY 43
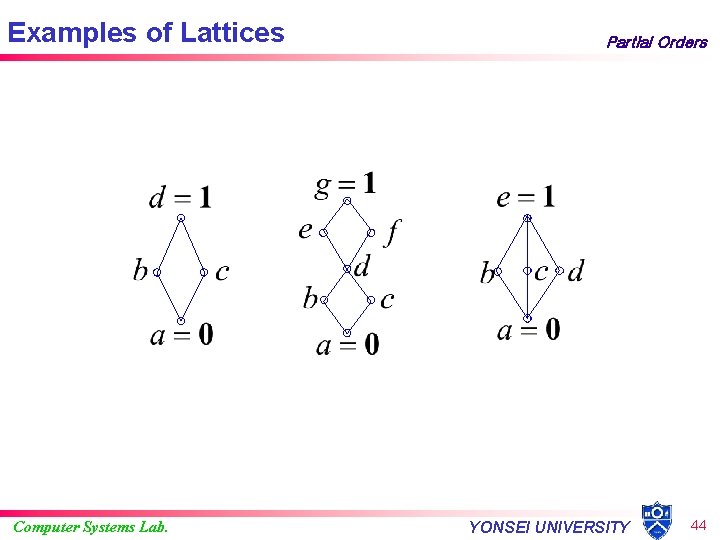
Examples of Lattices Computer Systems Lab. Partial Orders YONSEI UNIVERSITY 44

More Notation Partial Orders • “There Exists a in set ” is denoted by • The following are equivalent: ( ( ) ) • Does make sense in a poset? No--Complement is defined for lattices but not for posets Computer Systems Lab. YONSEI UNIVERSITY 45

Properties of Lattices Partial Orders Meet, Join, Unique maximum (1), minimum (0) element are always defined Idempotent: Commutative: Associative: Absorptive: Absorptive properties are fundamental to optimization Computer Systems Lab. YONSEI UNIVERSITY 46

Duality Partial Orders Every lattice identity is transformed into another identity by interchanging: • and Example: Computer Systems Lab. YONSEI UNIVERSITY 47

Complementation l l If x+y=1 and xy=0 then x is the complement of y and vice versa A lattice is complemented if all elements have a complement Computer Systems Lab. YONSEI UNIVERSITY 48
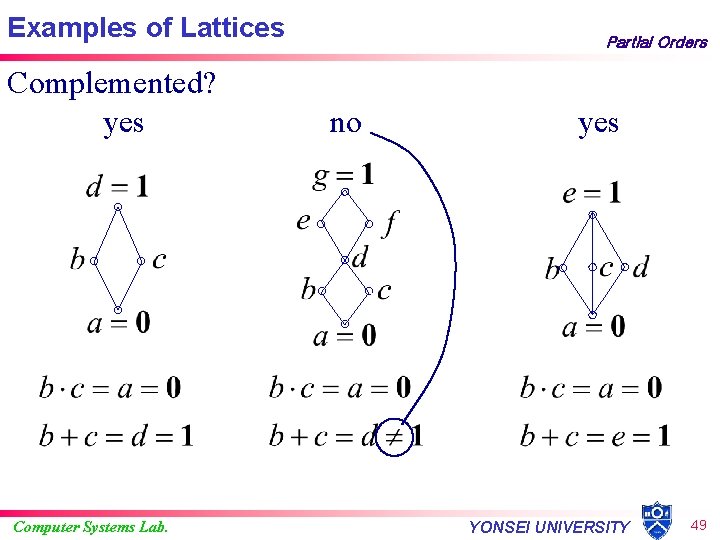
Examples of Lattices Complemented? yes Computer Systems Lab. Partial Orders no yes YONSEI UNIVERSITY 49

Distributivity Partial Orders Semi-distributivity: Proof : 1. 2. 3. 4. 5. Computer Systems Lab. (def. of meet) (def. of meet, join) (def. of meet) (mutatis mutandis: (def. of join) YONSEI UNIVERSITY ) 50

Distributivity Partial Orders • Boolean Algebras have full distributivity: • Boolean Algebras are complemented. That is, must hold for every Computer Systems Lab. in the carrier of the poset YONSEI UNIVERSITY 51

Definition of Boolean Algebra l Partial Orders A complemented, distributive lattice is a Boolean lattice or Boolean algebra § § § Idempotent x+x=x Commutative x+y=y+x Associative x+(y+z)=(x+y)+z Absorptive x(x+y)=x Distributive x+(yz)=(x+y)(x+z) Existence of the complement Computer Systems Lab. xx=x xy = yx x(yz) = (xy)z x+(xy) = x x(y+z) = xy +xz YONSEI UNIVERSITY 52

Are these Lattices Boolean Algebras? Complemented and distributed? yes no Computer Systems Lab. Partial Orders no YONSEI UNIVERSITY 53

Fundamental Theorem of Boolean Algebras Partial Orders • Every poset which is a Boolean Algebra has a power of 2 elements in its carrier • All Boolean Algebras are isomorphic to the power set of the carrier. Example: Computer Systems Lab. YONSEI UNIVERSITY 54

Examples of Boolean Algebras Partial Orders 1 -cube 2 -cube Computer Systems Lab. YONSEI UNIVERSITY 55

Atoms of a Boolean Algebra Partial Orders • A Boolean Algebra is a Distributive, Complemented Lattice • The minimal non-zero elements of a Boolean Algebra are called “atoms” 1 -atom 2 -atoms Can a Boolean Algebra have 0 atoms? Computer Systems Lab. NO! YONSEI UNIVERSITY 56
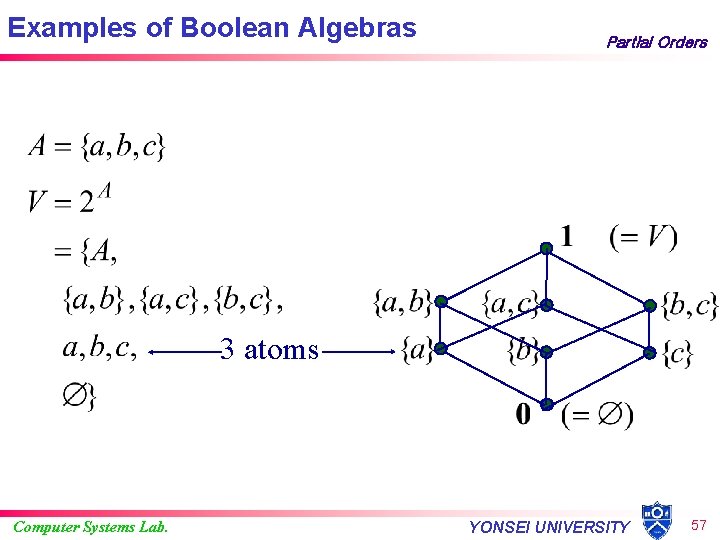
Examples of Boolean Algebras Partial Orders 3 atoms Computer Systems Lab. YONSEI UNIVERSITY 57

Examples of Boolean Algebras Level 4 --1 elt* Level 3 --4 elts Level 2 --6 elts Level 1 --4 elts Level 0 --1 elts Computer Systems Lab. Partial Orders * “elt” = element YONSEI UNIVERSITY 58

Boolean Algebras Theorem 3. 2. 6 proof: Suppose of ( Partial Orders Complementation is unique. and are both complements ). Hence Note we used distributivity. Similarly, we have Theorem 3. 2. 7 (Involution): Computer Systems Lab. YONSEI UNIVERSITY 59

Properties of Boolean Algebra l l Partial Orders x + x’y = x+y x(x’+y) = xy Computer Systems Lab. YONSEI UNIVERSITY 60

Lemma: The Isotone Property Partial Orders Proof: By Theorem 3. 2. 2, , so we get. Note we used idempotence, commutativity, and associativity. Then we use Theorem 3. 2. 2 again to prove the lemma. Computer Systems Lab. YONSEI UNIVERSITY 61

Duality for Boolean Algebras Partial Orders Every Boolean Algebra identity is transformed into another valid identity by interchanging: • and This rule not valid for lattices Example: Computer Systems Lab. YONSEI UNIVERSITY 62

Theorem Partial Orders Proof: By the isotone property we have The second identity follows by duality. Computer Systems Lab. YONSEI UNIVERSITY 63

Other Theorems Partial Orders De. Morgan’s Laws Consensus Computer Systems Lab. YONSEI UNIVERSITY 64

Consensus Examples Partial Orders 1. 3. Note use of De. Morgan’s Law Computer Systems Lab. YONSEI UNIVERSITY 65

Consensus Example Partial Orders 5. Is wrong. Replace by • Uphill Move: Note addition of redundant consensus term enables deletion of two other terms by consensus • This avoids local minima--a crucial part of the logic minimization paradigm Computer Systems Lab. YONSEI UNIVERSITY 66

Functions and Boolean Functions Ordinary functions of 1 variable: Ordinary functions of 2 real variables: Computer Systems Lab. YONSEI UNIVERSITY 67

Functions and Boolean Functions Boolean functions of Computer Systems Lab. Boolean Functions variables: YONSEI UNIVERSITY 68

Boolean Formulae Boolean Functions Boolean Formulae: Meets and Joins of Variables and Constants Computer Systems Lab. YONSEI UNIVERSITY 69

n-variable Boolean Formulae Boolean Functions The elements of are Boolean formulae. • Each variable is a Boolean formula. • If and are Boolean formulae, then so are • • A string is a Boolean formula if and only if it derives from finitely many applications of these rules. • Computer Systems Lab. YONSEI UNIVERSITY 70

Distinct Formulas, Same Function Boolean Functions Truth Table for 0000 0 ab 1 Computer Systems Lab. aaaa 0 ab 1 aa 11 bbbb 0 ab 1 b 1 b 1 1111 0 ab 1 1111 YONSEI UNIVERSITY 71

Boolean Functions on Boolean Algebra Boolean Functions • is a Boolean function • is also • If and are Boolean, functions then so are • • A function is Boolean if and only if it derives from finitely many applications of these rules. Computer Systems Lab. YONSEI UNIVERSITY 72

Cofactors Boolean Functions Positive Cofactor WRT : Negative Cofactor WRT : Note: prime denotes complement Computer Systems Lab. YONSEI UNIVERSITY 73

Cofactors Boolean Functions Positive Cofactor WRT : Negative Cofactor WRT : Example: This term drops out when is replaced by This term is unaffected Computer Systems Lab. YONSEI UNIVERSITY 74

Cofactors Boolean Functions Example: Computer Systems Lab. YONSEI UNIVERSITY 75

Boole’s Expansion Theorem Boolean Functions Example: Sum form: Product form: Computer Systems Lab. YONSEI UNIVERSITY 76

Variables and Constants Boolean Functions • In the previous slide and were constants, and the were variables. • But we can also use letters like and as variables, without explicitly stating what the elements of the Boolean Algebra are. Computer Systems Lab. YONSEI UNIVERSITY 77

Boole’s Expansion (Sum Form) Computer Systems Lab. Boolean Functions YONSEI UNIVERSITY 78

Boole’s Expansion (Product Form) Boolean Functions Note application of absorptive law Computer Systems Lab. YONSEI UNIVERSITY 79

Minterm Canonical Form Boolean Functions The minterm canonical form is a canonical, or standard way of representing functions. From p 100, is represented by millions of distinct Boolean formulas, but just 1 minterm canonical form. Note Thus some texts refer to f as {0, 1, 3, 4, 5, 6, 7} Computer Systems Lab. YONSEI UNIVERSITY 80
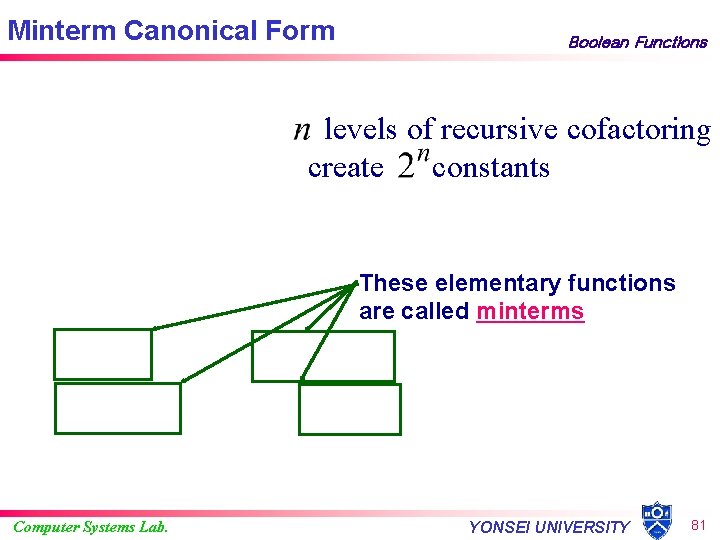
Minterm Canonical Form Boolean Functions levels of recursive cofactoring create constants These elementary functions are called minterms Computer Systems Lab. YONSEI UNIVERSITY 81

Minterm Canonical Form Boolean Functions Thus a Boolean function is uniquely determined by its values at the corner points These constants are aptly called discrimants Computer Systems Lab. YONSEI UNIVERSITY 82

Minterm Canonical Form Boolean Functions This function is Boolean (from Boolean Formula) 0000 0 ab 1 aa 11 Ý Ý aaaa 0 ab 1 00 bb bbbb 0 ab 1 aa 11 1111 0 ab 1 00 bb Ý Ý Thus all 16 cofactors match--not just discriminants Computer Systems Lab. YONSEI UNIVERSITY 83

Now Suppose Truth Table is Given Boolean Functions • Here we change 15 th cofactor, but leave the 4 discriminants unchanged • Since the given function doesn’t match at all 16 cofactors, is not Boolean 0000 0 ab 1 aa 11 Ý Computer Systems Lab. Ý aaaa 0 ab 1 00 bb bbbb 0 ab 1 aa 11 1111 0 ab 1 001 b 00 bb Ý YONSEI UNIVERSITY Ý 84

2 -Variable Boolean Functions Minterms 2 -variable functions 4 3 2 1 0 Note that the minterms just depend on the number and names of the variables, independent of the particular Boolean Algebra Computer Systems Lab. YONSEI UNIVERSITY 85

Boolean Function Algebras Boolean Functions The notation Fn(B) means “the Boolean Algebra whose carrier is the set of all n-variable Boolean Functions” which map B into Fn(B): Bn |-> B minterms If the atoms of Fn(B) are its n-variable B is called the “Base Algebra” of the Boolean Function algebra The atoms of B are called Base Atoms Computer Systems Lab. YONSEI UNIVERSITY 86
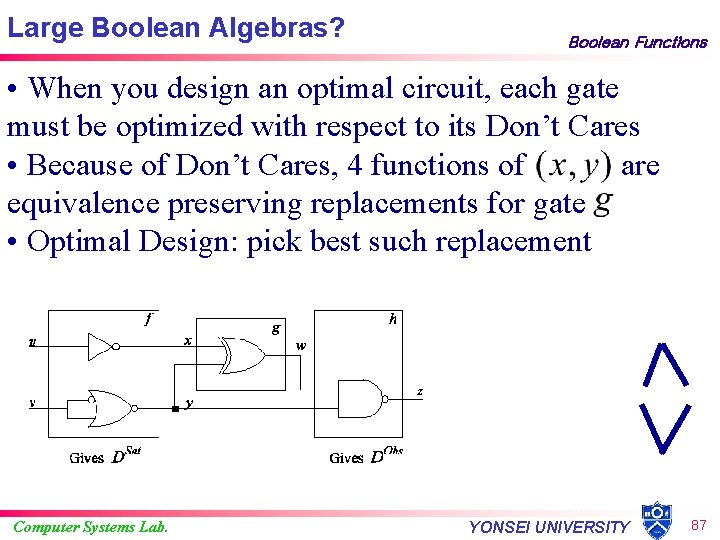
Large Boolean Algebras? Boolean Functions • When you design an optimal circuit, each gate must be optimized with respect to its Don’t Cares • Because of Don’t Cares, 4 functions of are equivalence preserving replacements for gate • Optimal Design: pick best such replacement Computer Systems Lab. YONSEI UNIVERSITY 87

Boolean Algebra Boolean Functions Level (= # of atoms) 4 3 Each element has 3 Atoms 2 Each element has 2 Atoms 1 Computer Systems Lab. Each element has 1 Atom Note: base atoms act like 2 extra literals YONSEI UNIVERSITY 88

Boolean Algebra Boolean Functions Level (= # of atoms) 4 3 3 minterms (3 atoms) 2 2 minterms (2 atoms) 1 1 minterm (1 atom) Computer Systems Lab. YONSEI UNIVERSITY 89

Boolean Algebra Boolean Functions Boolean Algebra 1 -Variable Functions of 3 Atoms 2 Atoms 1 Atom Subalgebras are incompletely specified Boolean Functions (most important) Computer Systems Lab. YONSEI UNIVERSITY 90
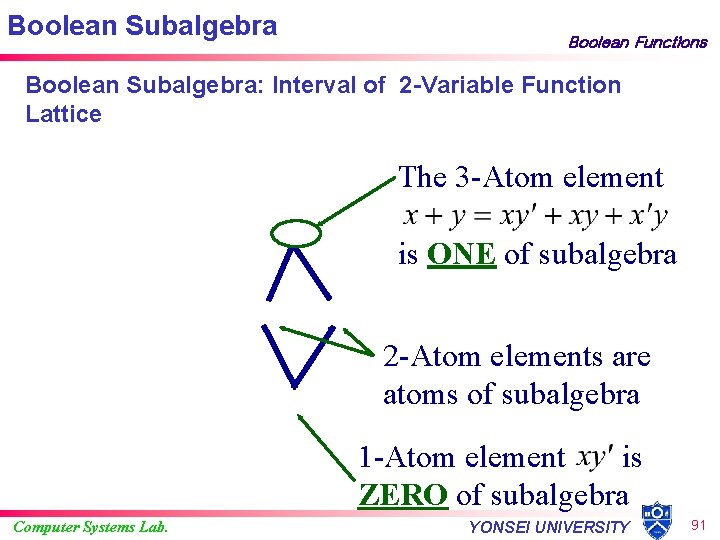
Boolean Subalgebra Boolean Functions Boolean Subalgebra: Interval of 2 -Variable Function Lattice The 3 -Atom element is ONE of subalgebra 2 -Atom elements are atoms of subalgebra 1 -Atom element is ZERO of subalgebra Computer Systems Lab. YONSEI UNIVERSITY 91

More On Counting Level (= # of atoms) 4 3 Boolean Functions An algebra (or subalgebra) with levels has exactly elements, because levels implies atoms 2 1 Computer Systems Lab. YONSEI UNIVERSITY 92
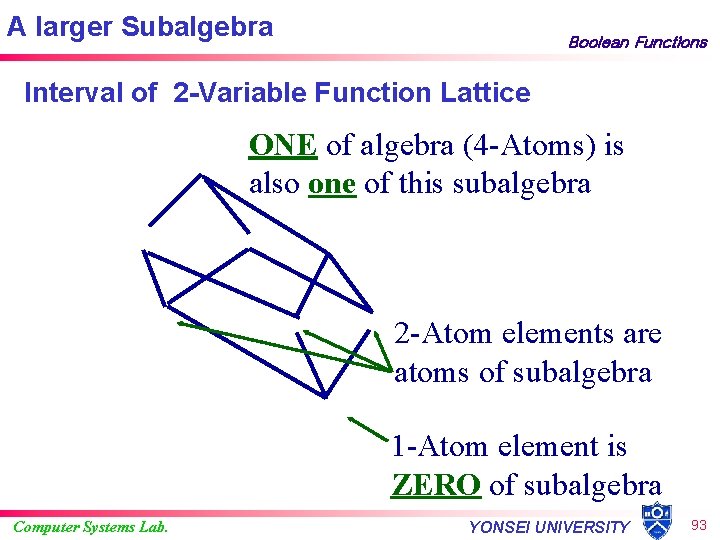
A larger Subalgebra Boolean Functions Interval of 2 -Variable Function Lattice ONE of algebra (4 -Atoms) is also one of this subalgebra 2 -Atom elements are atoms of subalgebra 1 -Atom element is ZERO of subalgebra Computer Systems Lab. YONSEI UNIVERSITY 93

Counting Elements of l l l Boolean Functions For each of the minterms, the discriminant can be chosen as any of the elements of. Therefore, the number of elements of is Examples Computer Systems Lab. YONSEI UNIVERSITY 94

Counting Elements of Fn(B) l Boolean Functions Examples with l Note 2(4) base atoms act like 1(2) extra variables Computer Systems Lab. YONSEI UNIVERSITY 95

Boolean Difference (Sensitivity) Boolean Functions A Boolean function depends on and only if. Thus if is called the Boolean Difference, or Sensitivity of with respect to Computer Systems Lab. YONSEI UNIVERSITY 96

Boolean Difference (Sensitivity) Boolean Functions Example: Note the formula depends on implied function does not Computer Systems Lab. , but the YONSEI UNIVERSITY 97
![Don’t Care l l l Don't Cares An interval [L, U] in a Boolean Don’t Care l l l Don't Cares An interval [L, U] in a Boolean](http://slidetodoc.com/presentation_image_h2/0d225581d1f24ab1000266ec6c2dc139/image-98.jpg)
Don’t Care l l l Don't Cares An interval [L, U] in a Boolean algebra B is the subset of B defined by [L, U] = { x B : L x U } Satisfiability don’t cares Observability don’t cares Computer Systems Lab. YONSEI UNIVERSITY 98

Intervals and Don’t Cares Computer Systems Lab. Incomplete Specifications YONSEI UNIVERSITY 99

Don’t Cares Don't Cares if and only if for all possible Input Filter Output Filter input if and only if local never occurs The complete don’t care set for gate Computer Systems Lab. . is YONSEI UNIVERSITY 100

Don’t Cares Don't Cares Local inputs For this circuit, local input combinations do not occur. That is, the local minterm is don’t care. Computer Systems Lab. YONSEI UNIVERSITY 101

Don’t Cares Don't Cares For this circuit, global input combination 10 sets which makes insensitive to. However, local input pair 10 ( ) is NOT don’t care, since also gives , and in this case. Computer Systems Lab. YONSEI UNIVERSITY 102

Computing ALL Don’t Cares Don't Cares if and only and does not occur for any row in the truth table. Here, ( does not occur) Computer Systems Lab. YONSEI UNIVERSITY 103

Computing ALL Don’t Cares Don't Cares Note these differ! Similarly that if and only for every row and , Here 10 ( ) is NOT don’t care since the first row. Computer Systems Lab. YONSEI UNIVERSITY such in 104

Computing ALL Don’t Cares Don't Cares Note these differ! Thus the exclusive OR gate can be replaced by a NAND Computer Systems Lab. YONSEI UNIVERSITY 105

Don’t Cares and Function Subalgebras Don't Cares Suppose we are given a Boolean Function and a don’t care set. Then any function in the interval (subalgebra) is an acceptable replacement for in the environment that produced. Here is the 0 of the subalgebra and is the 1. Computer Systems Lab. YONSEI UNIVERSITY 106

Incompletely Specified Functions Incomplete Specifications Suppose we are given a Boolean Function a don’t care set. Then the triple where , , and an Incompletely specified function. Note Computer Systems Lab. and is called. YONSEI UNIVERSITY 107
- Slides: 107