Boolean Algebra Purpose of BA is to facilitates
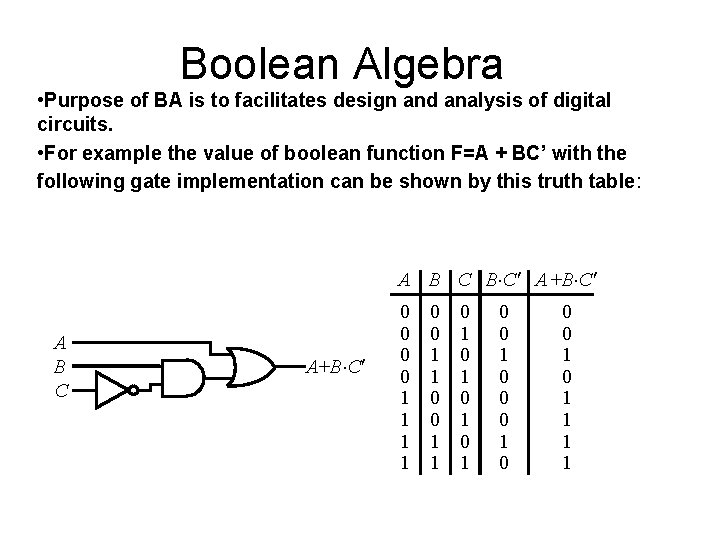
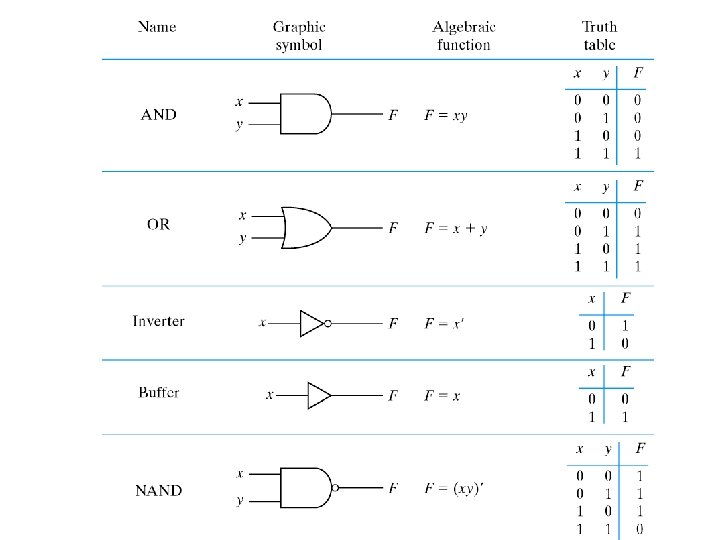
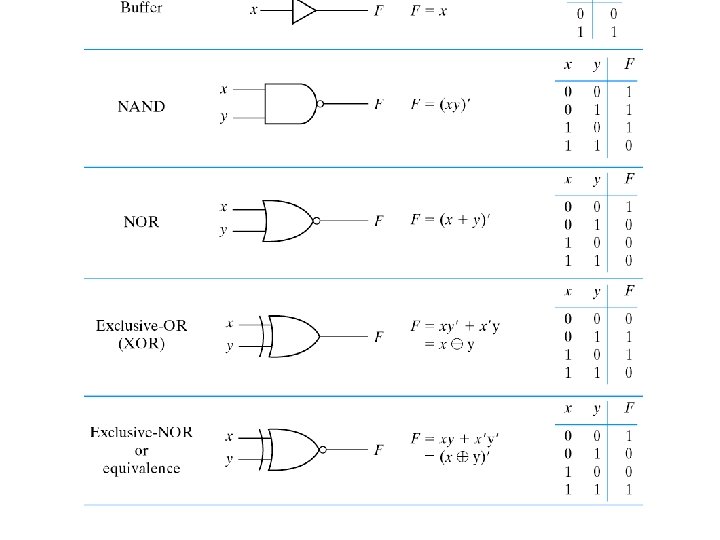
Boolean Algebra • Purpose of BA is to facilitates design and analysis of digital circuits. • For example the value of boolean function F=A + BC’ with the following gate implementation can be shown by this truth table: A B C B×C A+B×C A B C A+B×C 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1

Boolean Algebra • Basic identities of boolean algebra 1. X + 0 = X 2. X× 1 = X identity 3. X + 1 = 1 4. X× 0 = 0 base 5. X + X = X 6. X×X = X idempotence 7. X + X ’ = 1 excluded middle 8. X×X’ = 0 non contradiction 9. (X ’)’ = X involution 10. X + Y = Y + X 11. X×Y = Y×X commutative 12. X+(Y+Z ) = (X+Y )+Z 13. X×(Y×Z ) = (X×Y )×Z associative 14. X(Y+Z ) = X×Y + X×Z 15. X+(Y×Z ) = (X+Y )×(X+Z ) distributive 16. (X + Y ) = X ×Y 17. (X×Y)’ = X +Y demorgan 18. X + XY = X 19. X. (X+Y) = x absorbtion
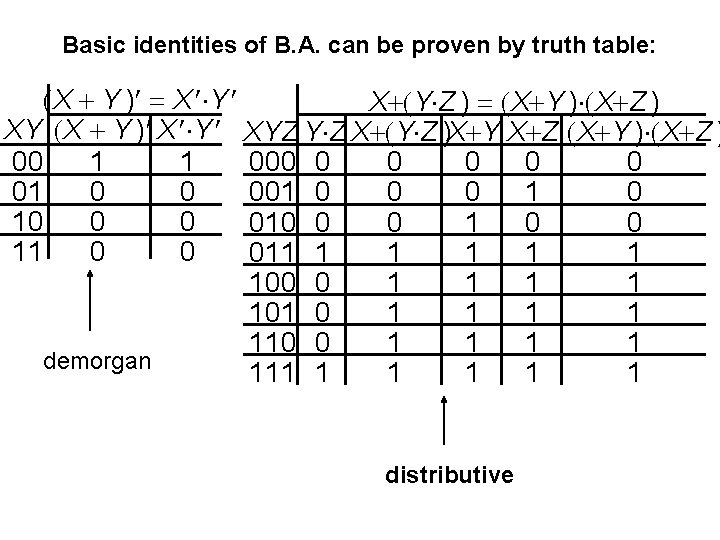
Basic identities of B. A. can be proven by truth table: (X + Y ) = X ×Y X+(Y×Z ) = (X+Y )×(X+Z ) XY (X + Y ) X ×Y XYZ Y×Z X+(Y×Z )X+Y X+Z (X+Y )×(X+Z ) 1 1 00 0 0 0 01 0 0 0 1 0 10 0 0 010 0 0 11 0 0 011 1 1 100 0 1 1 101 0 1 1 110 0 1 1 demorgan 111 1 1 distributive

Boolean Algebra • For each algebraic expression the dual of of algebraic expression achieved by interchanging AND and OR operators and replacing 0’s and 1’s. • Parallel columns illustrate duality principle. The duality principle states that if E 1 and E 2 are Boolean expressions then E 1= E 2 dual (E 1)=dual (E 2) where dual(E) is the dual of E • Note: 15 -17 have no counterpart in ordinary algebra. • Other handy identity. X+X’Y=X+Y (15, 7 and 2)

Boolean Algebra • By using boolean algebra rules, a simpler expression may be obtained • Operator Precedence: when evaluating boolean expression , order of precedence is: 1. Parentheses 2. NOT 3. AND 4. OR For example : Look at De. Morgan truth table first (x+Y) is computed then complement of (X+Y). But for x’. y’ first the complement of x and complement of y is computed and then the result is ANDed
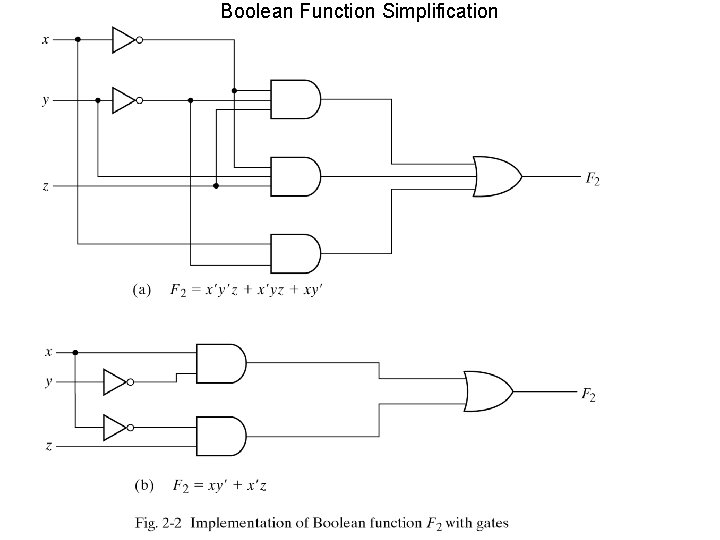
Boolean Function Simplification

Boolean function simplification • It means by manipulation of B. A. reducing the number of terms and literals in the function. For example: f= x’y’z + x’yz + xy’ = x’(y’z + yz) + xy’ = x’ (z(y’+y)) + xy’ = x’(z. 1) +xy’ = x’z + xy’

The Consensus Theorem. XY +YZ + X Z = XY + X Z Proof. XY +YZ + X Z = XY + (X + X )YZ + X Z 2, 7 = XY + XYZ + X Z 14 = XY(1 + Z ) + X Z(Y + 1) 2, 11, 14 = XY + X Z 3, 2 Dual. (X + Y )(Y + Z )(X + Z ) = (X + Y )(X + Z )

Complement of a Function There are two ways for doing that: 1) Using De. Morgan’s theorem 2) Taking the dual of the function and complement each literal For example complements of x’yz’ + x’y’z = (x+y’+ z)(x+ y+z’) x(y’z’ + yz) = x’ + (y+z)(y’ + z’)

Canonical and standard Forms • The sum of products is one of two standard forms for Boolean expressions. sum-of-products-expression = p-term + p-term . . . + p-term = literal × ××× × literal – example. X Y Z + XYZ • A minterm is a term that contains every variable, in either complemented or un-complemented form. – example. in expression above, X Y Z is minterm, but X Z is not • A sum of minterms expression is a sum of products expression in which every term is a minterm. – example: X Y Z + X YZ + XYZ is sum of minterms expression that is equivalent to expression above. – shorthand : list minterms numerically, so X Y Z + X YZ + XYZ becomes 001+011+110+111 or Sm (1, 3, 6, 7)

Canonical and standard Forms • The product of sums is the second standard form for Boolean expressions. product-of-sums-expression = s-term × s-term . . . × s-term = literal + ××× + literal – example. (X +Y +Z )(X +Y +Z ) • A maxterm is a sum term that contains every variable, in complemented or uncomplemented form. – example. in exp. above, X +Y +Z is a maxterm, but X +Z is not • A product of maxterms expression is a product of sums expression in which every term is a maxterm. – example. (X +Y +Z )(X +Y+Z )(X+Y+Z ) is product of maxterms expression that is equivalent to expression above. – shorthand : list maxterms numerically: so, (X +Y +Z )(X +Y+Z) (X+Y+Z ) becomes 110+100+001+000 or – P M(6, 4, 1, 0)

How to build the boolean function from truth table • One way is to find a minterms or standard products by ANDing the terms of the n variable, each being primed if it is 0 and unprimed if it is 1. A boolean function can be formed by forming a minterm for each combination of variables that produce 1 in the function and then taking OR of all those forms. • Another way is by finding maxterms or standard sums by OR term of the n variables, with each variable being unprimed if corresponding bit is 0 and primed if it is 1. A boolean function can be formed as a product of maxterms for each combination of variables that produce 0 in the function and then form And of all those forms

For example: x y z function f 1 function f 2 minterms maxterms 0 0 0 m 0 M 0 0 0 1 1 0 m 1 M 1 0 0 0 m 2 M 2 0 1 1 0 1 m 3 M 3 1 0 0 1 0 m 4 M 4 1 0 1 m 5 M 5 1 1 0 0 1 m 6 M 6 1 1 1 m 7 M 7 Sum of minterms f 1 = x’y’z + xy’z’ + xyz = m 1 + m 4 + m 7 f 2= x’yz + xy’z + xyz’ + xyx = m 3 + m 5 + m 6 + m 7 Product of maxterms f 1= (x+y+ z)(x+y’+z)(x’+ y + z’)(x’ + y + z) = M 0 M 2 M 3 M 5 M 6 f 2= (x+y+z)(x+y+z’)(x+y’+z)(x’+y+z) = M 0 M 1 M 2 M 4

Conversion between Canonical Forms • By reading from a truth table the two canonical forms ( sum of minterms and product of maxterms) can be obtained. • A boolean function can be converted to the canonical form. For example: F= xy + x’y (in form of sum of the products S. O. P) = (z+ z’)xy + x’z(y+y) = xyz + xyz’ + x’zy’ can be converted to sum of minterms that can be shown by m 1+m 3+m 6+m 7 or ∑(1, 3, 6, 7)

Conversion between Canonical Forms • To convert it to the product of maxterms F= xy + x’y = (xy + x’)(xy +z) = (x’ + x) (x’+ y)(x+z)(y+z) = (x’+y)(x+z)(y+z) it is in the form of products of sums (P. O. S) but we want the product of maxterms. So = (x’+y+(z. z’)) (x + z + (y. y’))(y +z + (x. x’)) = (x’ + y + z)(x + z + y)(x+ z + y’)(x’ + y +z’) = M 0 M 2 M 4 M 5=∏(0, 2, 4, 5)

Conversion between Canonical Forms • To convert from one canonical form to another, interchange the symbol ∑ and ∏ and list those numbers missing from the total number of minterms or maxterms which is 2 n, where n is number of variables. • To verify that we convert sum of minterms to the product of maxterms by finding the complement of a function presented as sum of minterms. From the result the product of maxterms can be easily obtained For example: F(x, y, z) = m 1+m 3+m 6+m 7= ∑(1, 3, 6, 7) the complement of F (presented in the form of sum of the minterms) are the minterms that makes F to be zero thus F’(x, y, z) = (∑(1, 3, 6, 7))’= (m 0 + m 2 + m 4 + m 5) F = (F’(x, y, z))’ = (m 0 + m 2 + m 4 + m 5)’ Using Demorgan’s =m 0’m 2’m 4’m 5’= since each m’j = Mj it is M 0 M 2 M 4 M 5 = ∏(0, 2, 4, 5)

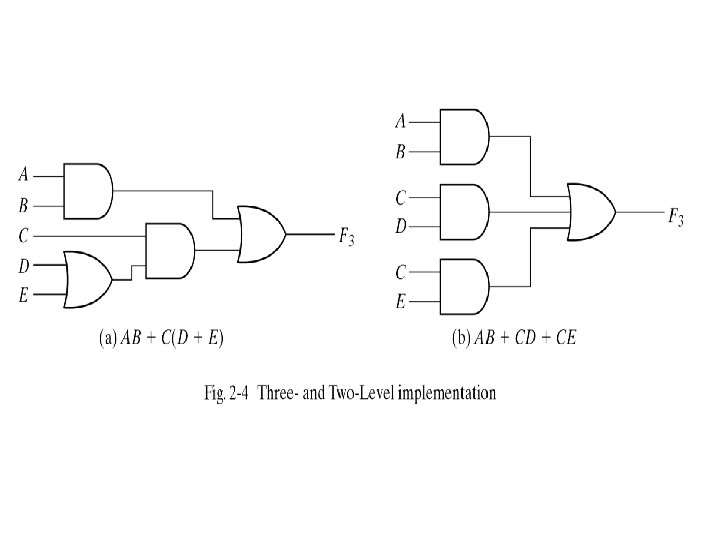
Standard forms • Sometimes boolean functions are shown as standard forms. For example: F 1 =y’ + xy + x’y’z’ ( sum of products) F 2 = x(y’ + z) (x’ + y + z’) (product of sums) the product and sum can be used to make the gate structure consist of AND and OR gates • Sometimes boolean function can be shown in non standard forms: F 3= AB + C(D + E) can be changed to AB + CD + CE • Different forms results different level of implementation of logical gates (see the next slide)
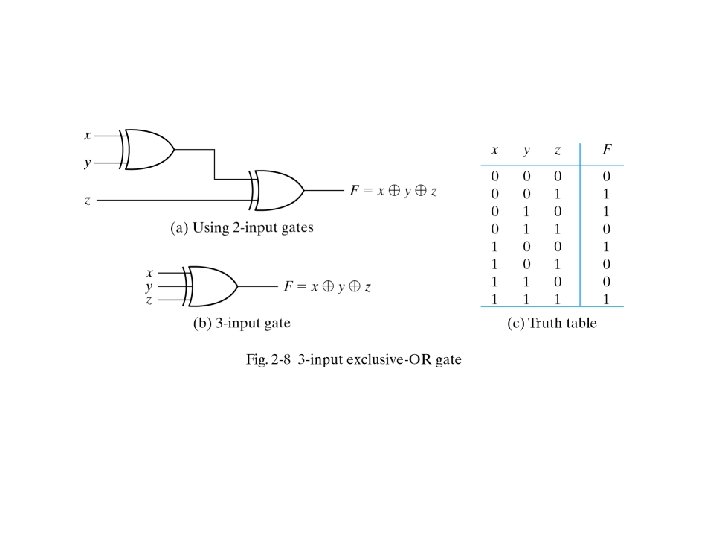
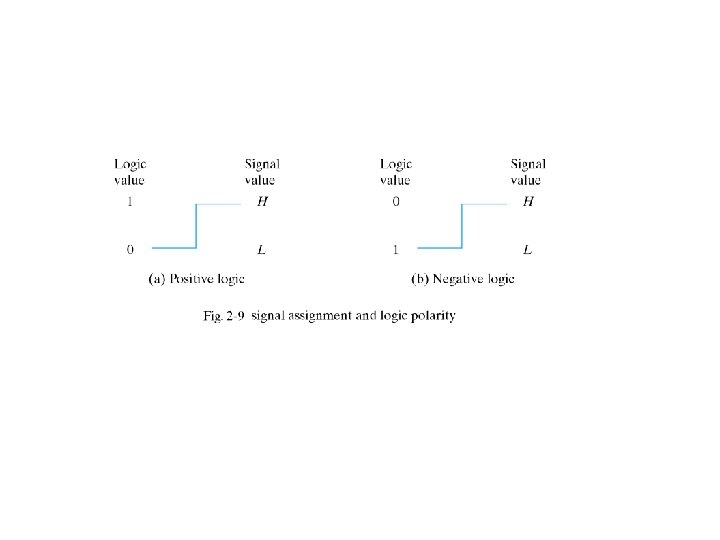
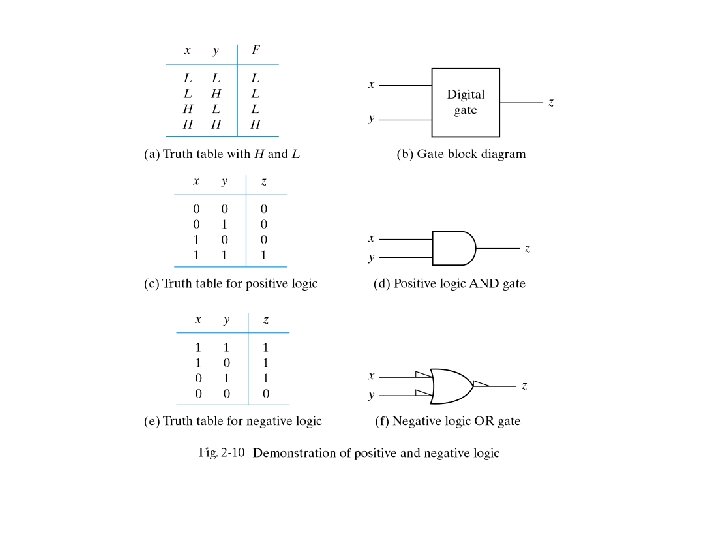
- Slides: 25