BOOLEAN ALGEBRA AND LOGIC SIMPLIFICATION By Kumutha Boolean

BOOLEAN ALGEBRA AND LOGIC SIMPLIFICATION By Kumutha…

Boolean Operations and Expression: Boolean algebra is the mathematics of digital systems. A basic knowledge of Boolean algebra is indispensable to the study and analysis of logic circuits. Terms used in Boolean Algebra: A variable is a symbol (usually an italic uppercase letter) used to represent a logical quantity. Any single variable can have a 1 or 0 value. The complement is the inverse of a variable and is indicated by a bar over the variable (overbar)

Law of Boolean Algebra The basic law of Boolean Algebra: The commutative laws The associative laws The distributive law for addition and multiplication are the same as in ordinary algebra. Each of the laws is illustrated with two or three variables, but the number of variables is not limited to this.

Commutative Laws of addition The commutative law of addition for two variables is written as A+B= B+A This law states that the order in which the variables are ORed makes no difference. This law is applied to the OR gate.

Commutative law of multiplication The commutative law of multiplication for two variables is AB=BA This law states that the order in which the variables are ANDed make no difference. This law as applied to the AND gate.

Associative Laws The associative law of addition is written as follows for three variables: A + (B+C) = (A+B)+C This law states that when OR more than two variables, the result is the same regardless of the grouping of the variables.

Associative law of multiplication The associative law of multiplication is written as follows for three variables: A(BC) = (AB)C This law states that it makes no difference in what order the variables are grouped when ANDing more two variables.

Distributive Laws The distributive law is written for three variables as follows: A(B+C) = AB + AC This law states that ORing two or more variables and then ANDing the result with a single variable is equivalent to ANDing the single variable with each of the two or more variables and then ORing the products. The distributive law also expresses the process of factoring in which the common variable A is factored out of the product terms.

Rules of Boolean Algebra
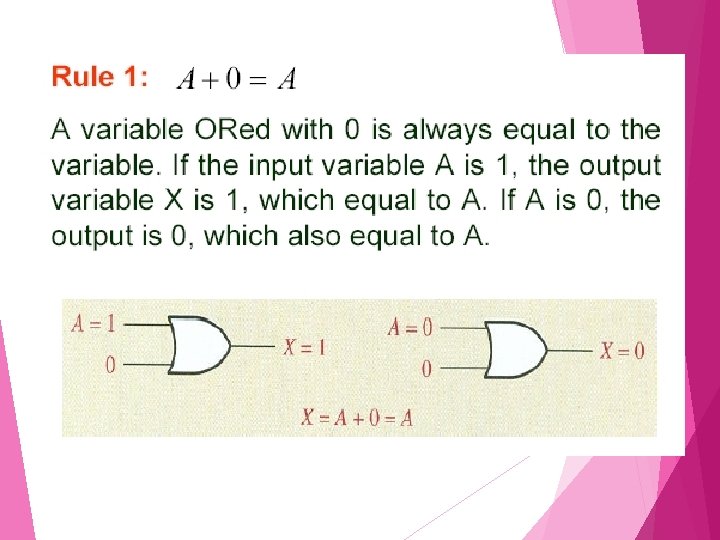
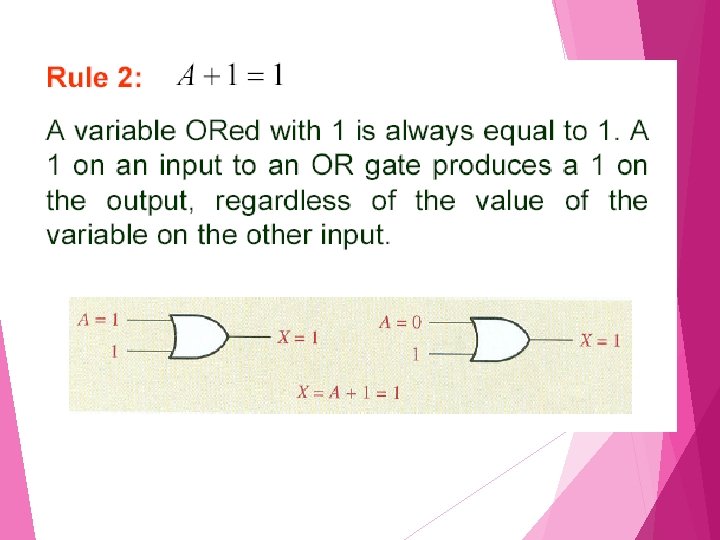
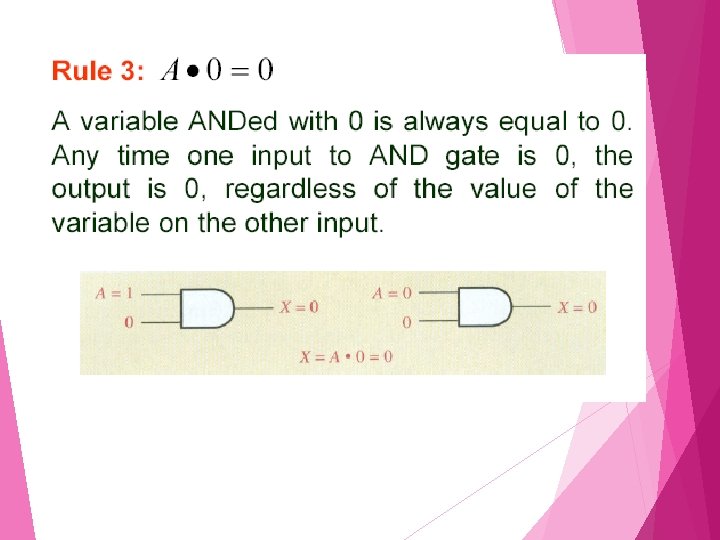
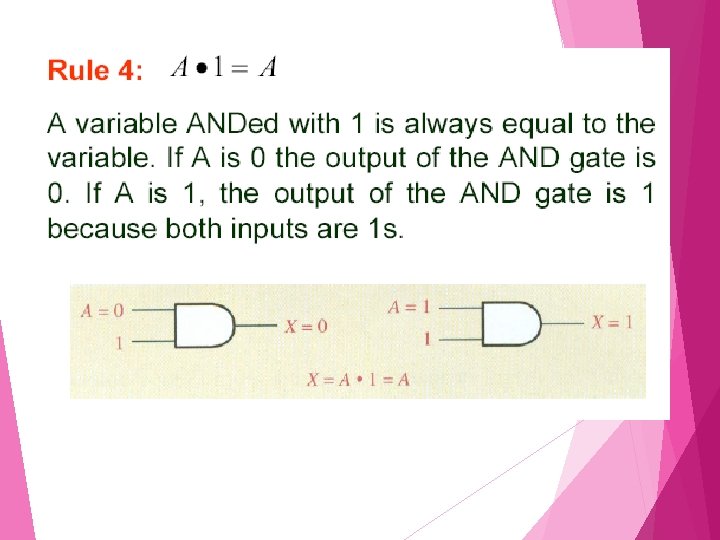
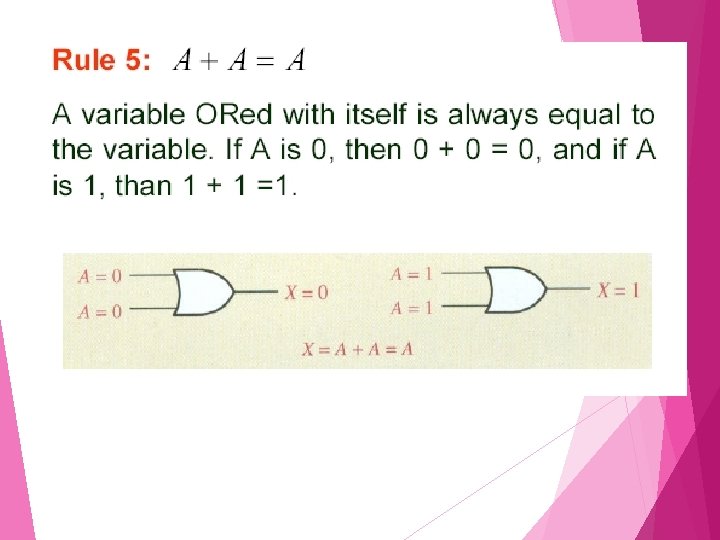

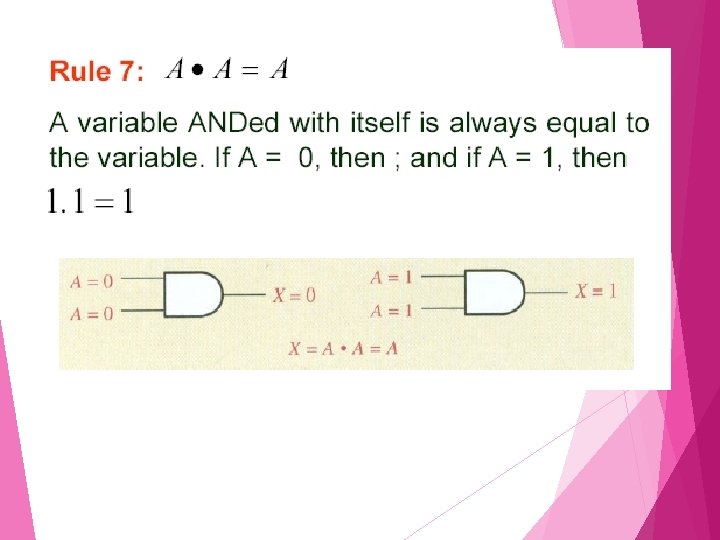
Rule 6:






Exercise 1 Simplify the Boolean Expression using Rules of Boolean Algebra a) AB(C+B) b) AB + ABC
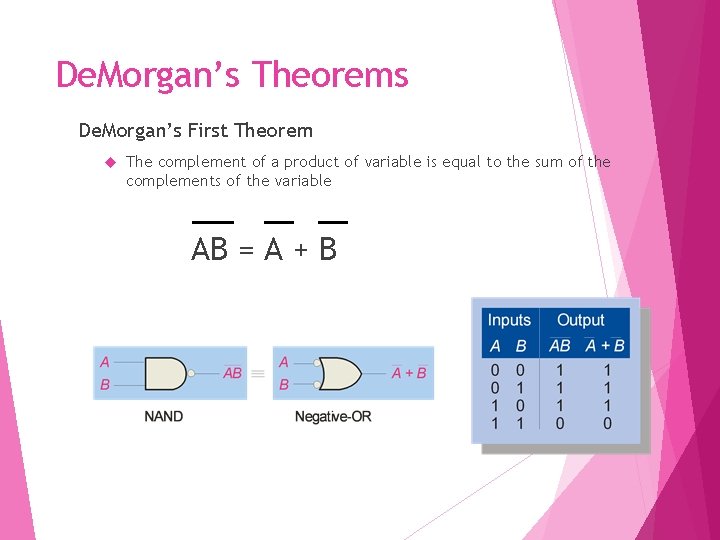
De. Morgan’s Theorems De. Morgan’s First Theorem The complement of a product of variable is equal to the sum of the complements of the variable AB = A + B

De. Morgan’s Theorems De. Morgan’s Second Theorem The complement of a sum of variables is equal to the product of the compliments of the variable A+B = A B

De. Morgan’s Theorems Example 1 Apply De. Morgan’s Theorem to the expression (A+B+C)D Let A+B+C = X and D = Y. So its equal to XY = X + Y and can be rewrite as (A+B+C)D = A + B + C + D Next, apply De. Morgan’s Theorem to term A + B + C A+B+C+D=ABC+D

Example 2

SOP and POS Form

• Standardexpression Non Standard expression

Example

POS Standard Form Example
- Slides: 30