Boolean Algebra and Gate Networks Modern digital computers

Boolean Algebra and Gate Networks • Modern digital computers are designed , maintained , and their operation is analyzed using techniques and symbology from a field of mathematics called modern algebra • The name Boolean algebra honors a fascinating English mathematics called modern algebra • Boolean algebra was first brought to bear on problems by Claude Shannon in 1938 (switching circuits)

Boolean Algebra & logic gates • In formula 2 x+5 y=z, in normal algebra (x, y and z may range through the entire field of real numbers) • In Boolean algebra , the variables take only one of two possible values ( 0 or 1). • So in equation x+y=z each of the variables x, y and z will be one of the values 0 or 1.

• The possible input and output combinations may be arranged as follows: • 0+0=0 • 0+1 =1 • 1+0 =1 • 1+1 =1 • This is called logical addition (+ OR)

• The second important operation in Boolean algebra is called (. AND) or Logical Multiplication. • 0. 0 =0 • 0. 1 =0 • 1. 0 =0 • 1. 1 =1 • Both (+) and (. ) Obey a mathematical rule called the associative law. • (x+y)+z = x +(y+z) • (x. y). z = x. (y. z)

• If +’s and. ’s mixed , then the rule which is used is that (. always performed before +) • So x. y+z = (x. y )+ z • And x. y + x. z means (x. y) + (x. z)

• The (. ) Operations are physically realized by electronic circuit called AND Gate • Logical Multiplication function Input A 0 0 1 1 B 0 1 Output F 0 0 0 1 • • • 1 output 2 inputs 3 inputs 4 inputs Multiple inputs A B F

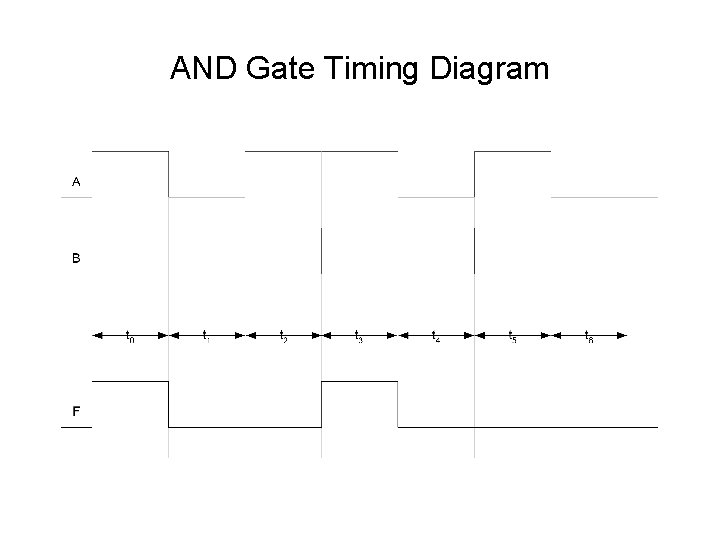
AND Gate Timing Diagram

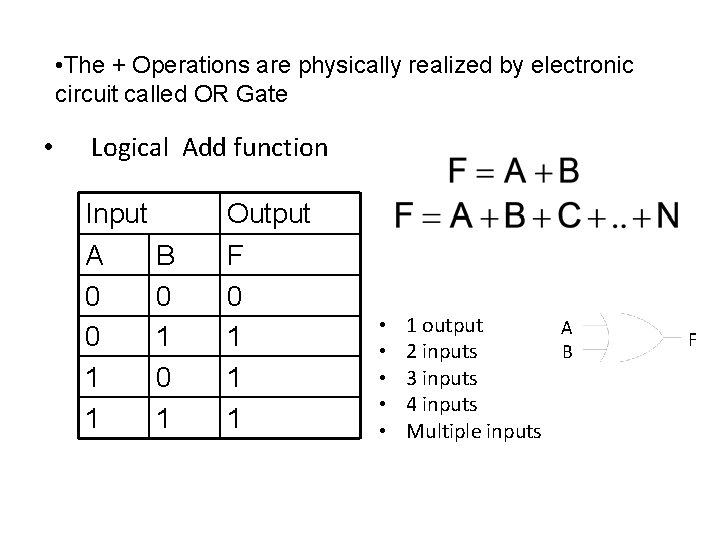
• The + Operations are physically realized by electronic circuit called OR Gate • Logical Add function Input A 0 0 1 1 B 0 1 Output F 0 1 1 1 • • • 1 output A B 2 inputs 3 inputs 4 inputs Multiple inputs F

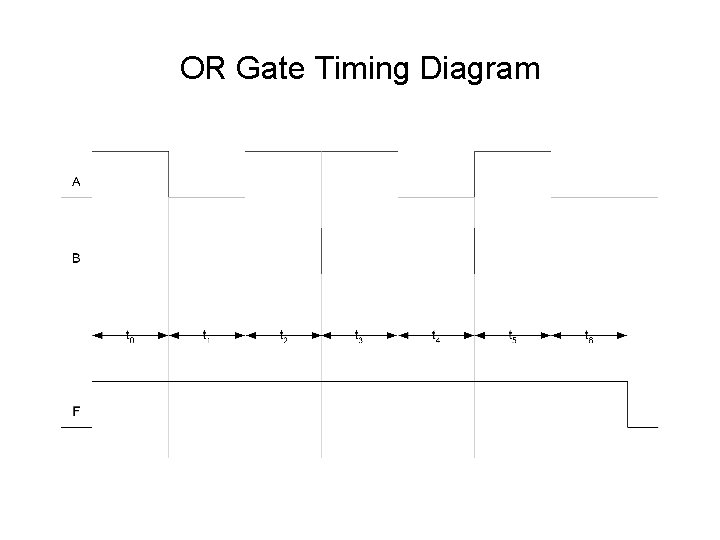
OR Gate Timing Diagram

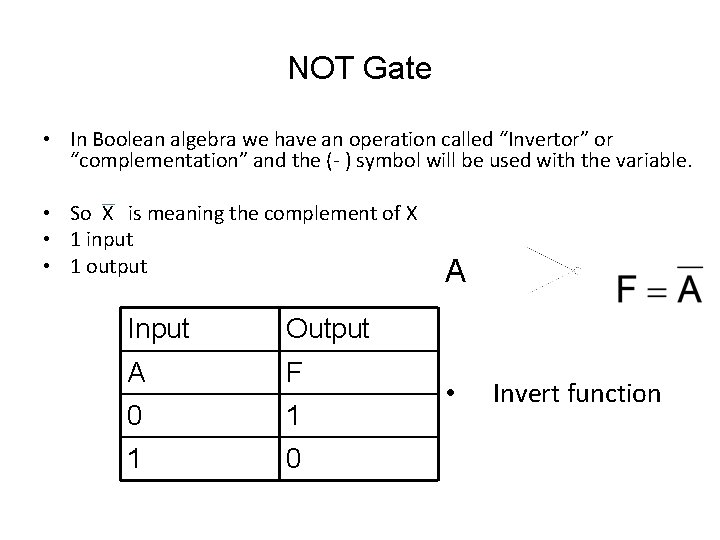
NOT Gate • In Boolean algebra we have an operation called “Invertor” or “complementation” and the (- ) symbol will be used with the variable. • So X is meaning the complement of X • 1 input • 1 output Input Output A F 0 1 1 0 A • Invert function

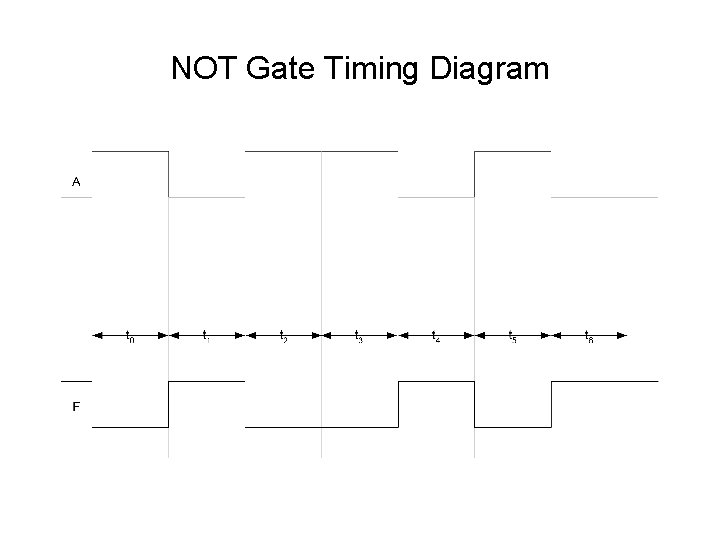
NOT Gate Timing Diagram

• The complement of a value can be taken repeatedly • 0 =1=0=1

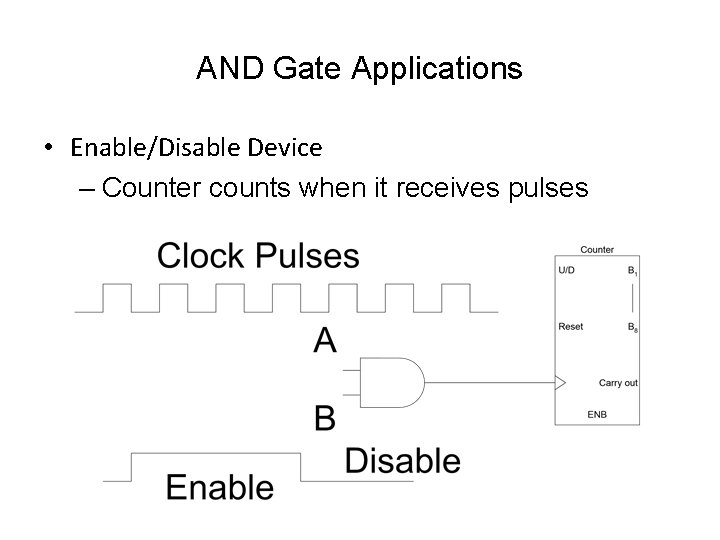
AND Gate Applications • Enable/Disable Device – Counter counts when it receives pulses

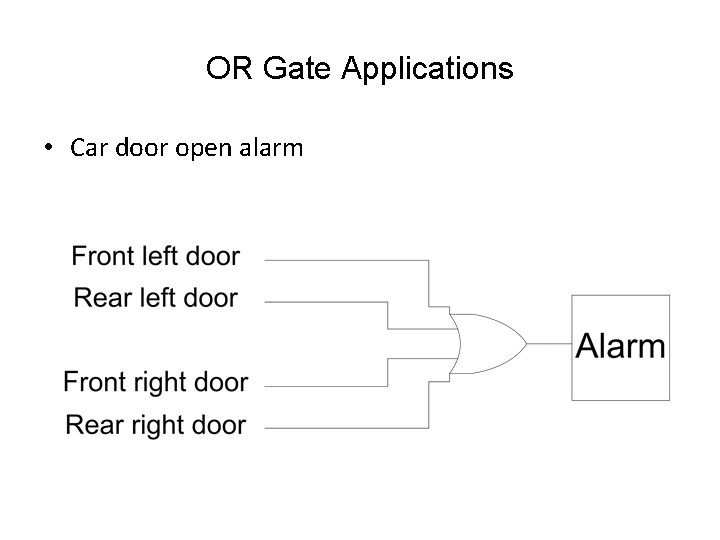
OR Gate Applications • Car door open alarm

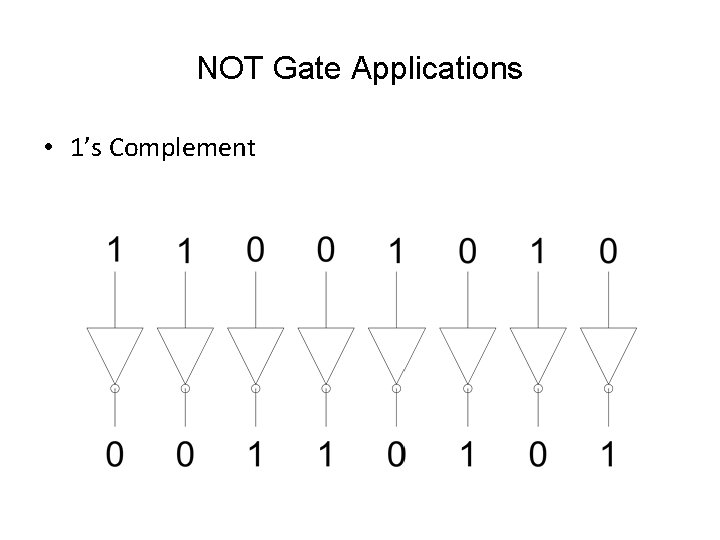
NOT Gate Applications • 1’s Complement

Evaluation of logical expressions • To study a logical expression it is very useful to construct a table of values (Truth table) for the variables then evaluate the expression for each of the possible combination of variables in turn • Consider the expression x+yz , there are 3 variables x, y, z so there are 2^3 combinations. X Y Z 0 0 0 1 1 1 0 0 1 1 1 ‘Z Y’Z X+Y’Z

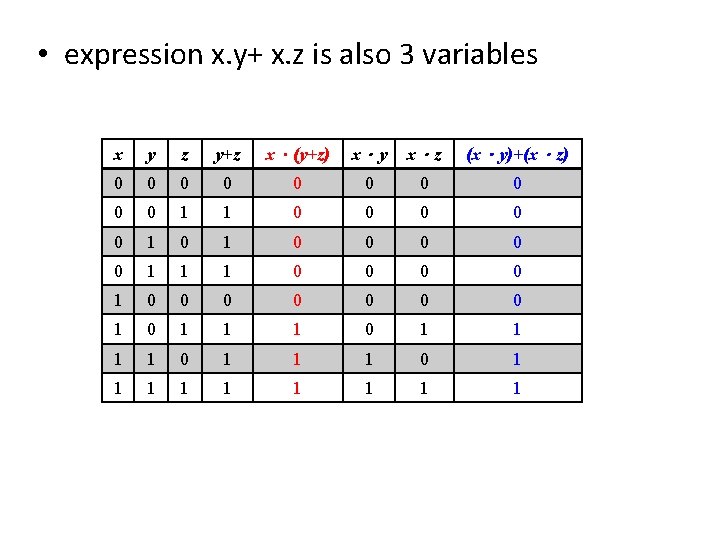
• expression x. y+ x. z is also 3 variables x y z y+z x．(y+z) x．y x．z (x．y)+(x．z) 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 0 1 1 1 1 1

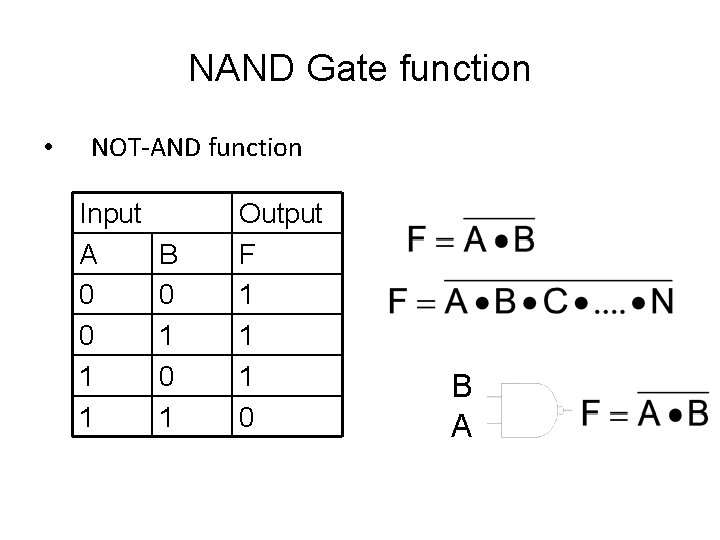
NAND Gate function • NOT-AND function Input A 0 0 1 1 B 0 1 Output F 1 1 1 0 B A

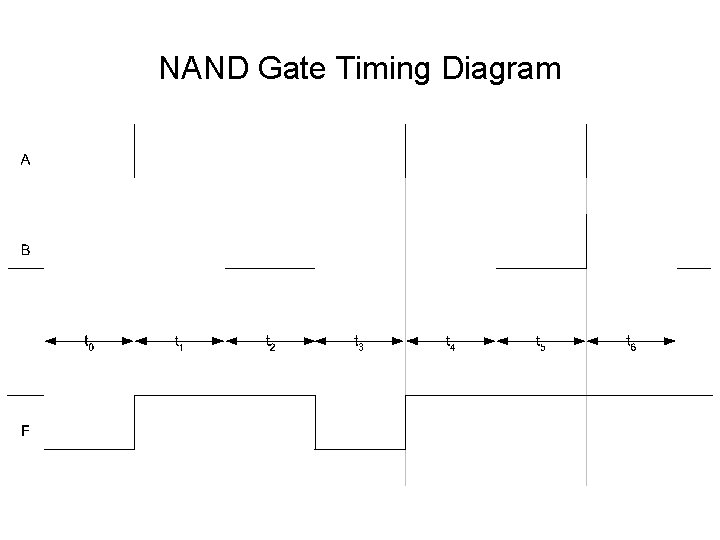
NAND Gate Timing Diagram

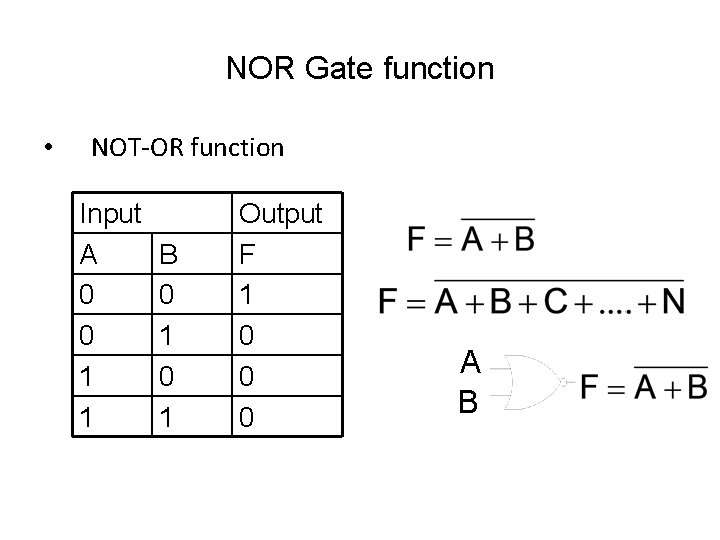
NOR Gate function • NOT-OR function Input A 0 0 1 1 B 0 1 Output F 1 0 0 0 A B

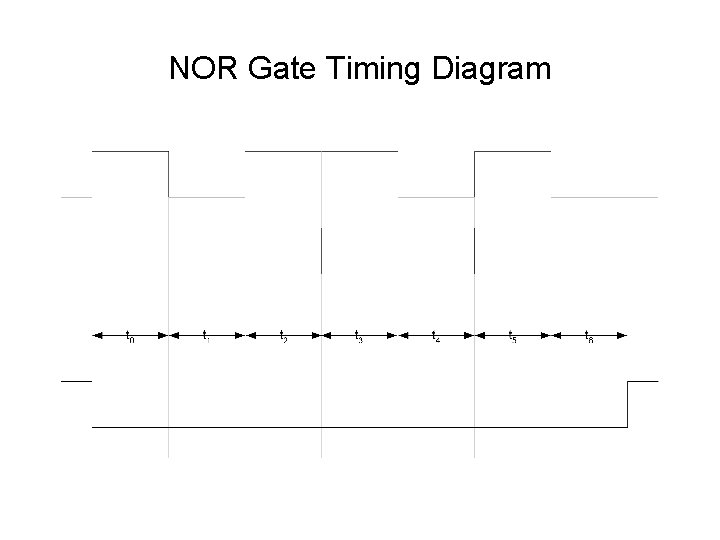
NOR Gate Timing Diagram