Boolean Algebra 1 The Laws of Boolean Algebra

Boolean Algebra 1 The Laws of Boolean Algebra
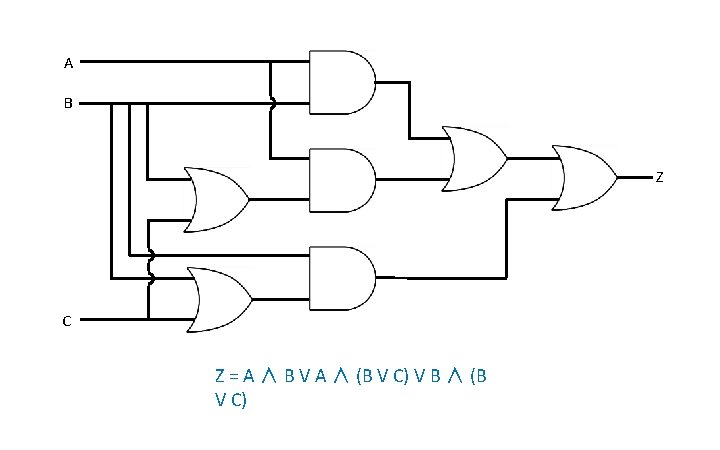
A B Z C Z = A ∧ B V A ∧ (B V C) V B ∧ (B V C)
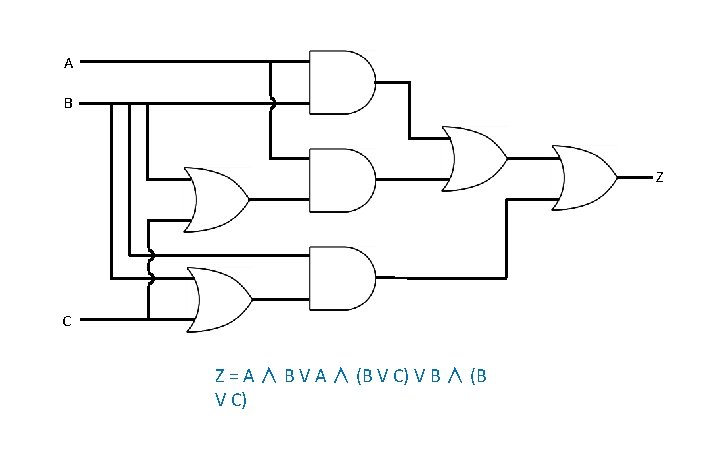
A B Z C Z = A ∧ B V A ∧ (B V C) V B ∧ (B V C)

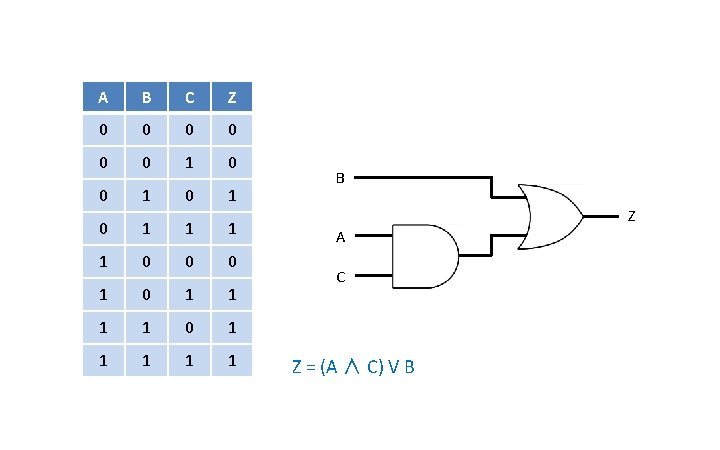
A B C Z 0 0 0 1 0 1 1 0 0 0 1 1 1 1 0 1 1 1 B Z A C Z = (A ∧ C) V B

The Laws of Boolean Algebra
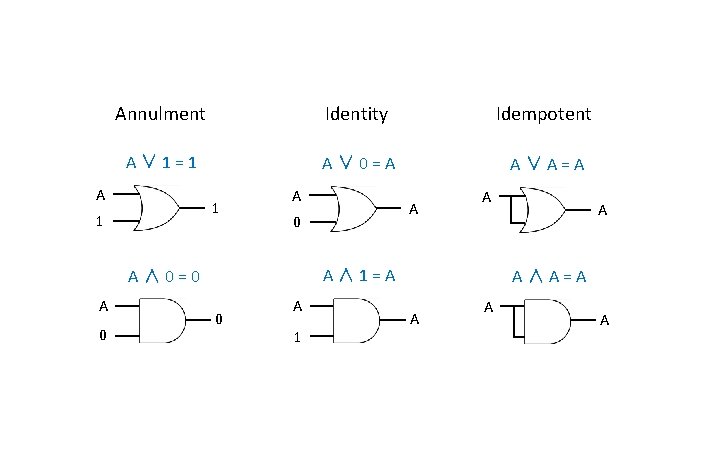
Annulment Identity Idempotent A∨ 1=1 A∨ 0=A A∨A=A A 1 1 A 0 0 A A∧ 1=A A∧ 0=0 A A 0 A 1 A A∧A=A A
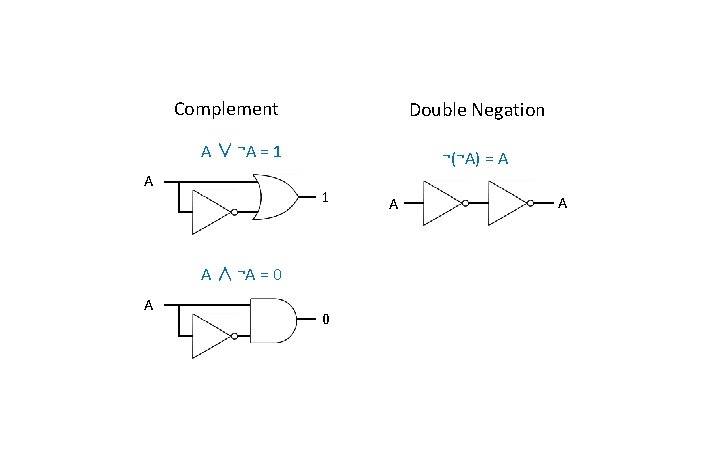
Complement Double Negation A ∨ ¬A = 1 A ¬(¬A) = A 1 A ∧ ¬A = 0 A A
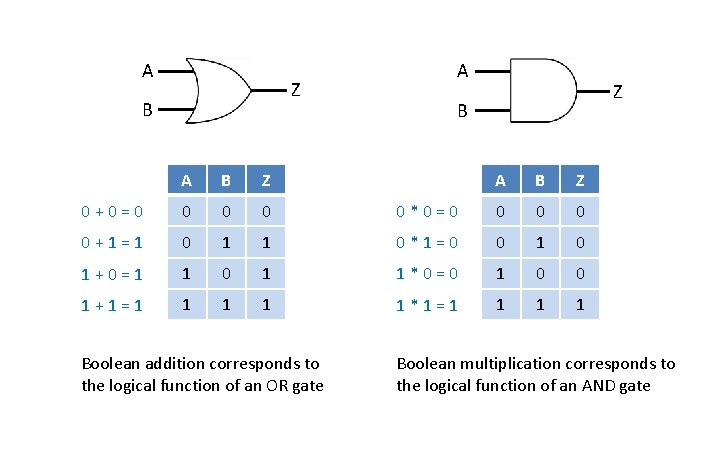
A Z B A B Z 0+0=0 0 0+1=1 0 1 1+0=1 1 1+1=1 1 A Z B A B Z 0*0=0 0 1 0*1=0 0 1 1*0=0 1 0 0 1 1 1*1=1 1 Boolean addition corresponds to the logical function of an OR gate Boolean multiplication corresponds to the logical function of an AND gate
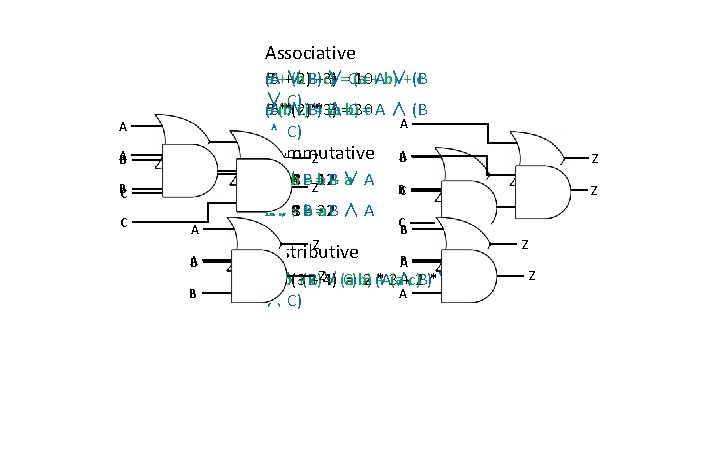
Associative (A++∨ (5 a 5 (b (2 2)B) ++c) 3) ∨ 3 =C(a 10 =+Ab) ∨+(B c ∨ C) (5(b a 5 (A **∧ (2 2)B) c) *=*3) ∧ (a 3 =b) C 30 =c A ∧ (B A ∧ C) A A B Commutative Z A B Z BC 8 +∨b 4 a 4 A 8 B=Z=b 12 B+ ∨ a A BC Z C A A B B 8 b*∧=8 a 4 A 4 Bb = =32 a. B ∧ A Z Distributive CB B A 2 a. A (b *∧(3 +(Bc) +Z∨ 4) = (a C) = b) =2 (A *+ 3(a ∧ +c)2 B)*∨ 4 (A A ∧ C) Z Z
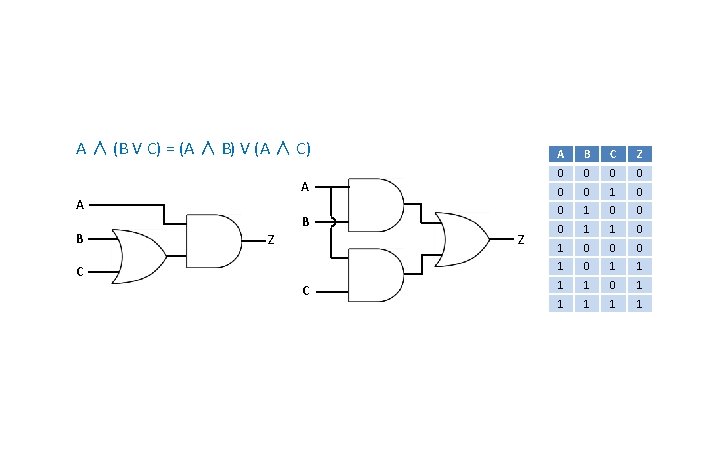
A ∧ (B V C) = (A ∧ B) V (A ∧ C) A A B B Z Z C C A B C Z 0 0 0 1 1 0 0 0 1 1 1 1 0 1 1 1
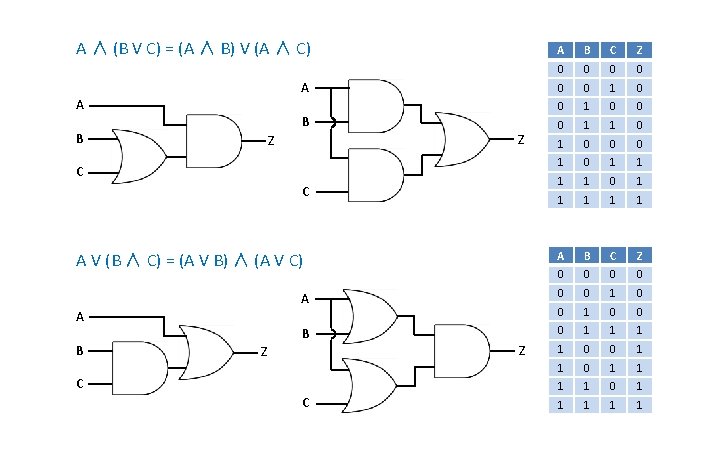
A ∧ (B V C) = (A ∧ B) V (A ∧ C) A B C Z 0 0 0 1 1 0 0 0 1 1 1 1 0 1 1 1 A B C Z 0 0 A 0 0 1 0 0 B 0 1 1 0 0 1 1 1 1 0 1 1 1 A A B B Z Z C C A V (B ∧ C) = (A V B) ∧ (A V C) A B Z C C Z

Associative (A ∨ B) ∨ C = A ∨ (B ∨ C) (A ∧ B) ∧ C = A ∧ (B ∧ C) Commutative A∨B=B∨A A∧B=B∧A Distributive A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)

Associative (A ∨ B) ∨ C = A ∨ (B ∨ C) (A ∧ B) ∧ C = A ∧ (B ∧ C) Commutative A∨B=B∨A A∧B=B∧A Distributive A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) Absorptive A ∨ (A ∧ B) = A A ∧ (A ∨ B) = A
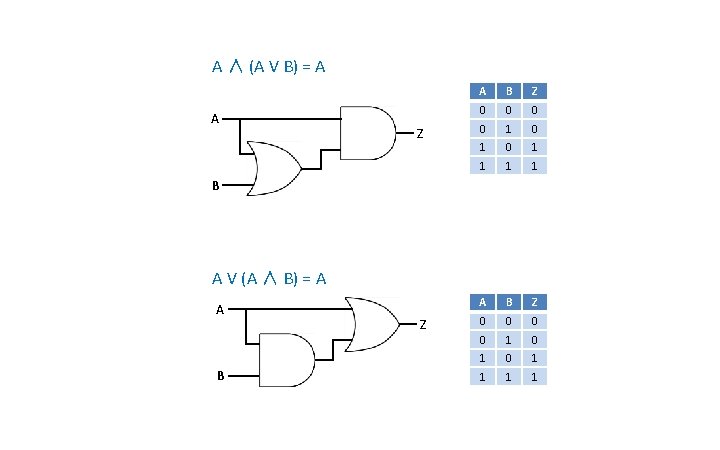
A ∧ (A V B) = A A Z A B Z 0 0 0 0 1 0 1 0 1 1 1 1 B A V (A ∧ B) = A A B Z

Associative (A ∨ B) ∨ C = A ∨ (B ∨ C) (A ∧ B) ∧ C = A ∧ (B ∧ C) Commutative A∨B=B∨A A∧B=B∧A Distributive A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) Absorptive A ∨ (A ∧ B) = A A ∧ (A ∨ B) = A

Complement A∧ 0=0 A ∨ ¬A = 1 Associative A∨ 1=1 A ∧ ¬A = 0 Identity Double Negation (A ∨ B) ∨ C = A ∨ (B ∨ C) (A ∧ B) ∧ C = A ∧ (B ∧ C) A∧ 1=A ¬(¬A) = A Annulment Commutative A∨B=B∨A A∨ 0=A A∧B=B∧A Idempotent Distributive A∨A=A A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) A∧A=A Absorptive A ∨ (A ∧ B) = A A ∧ (A ∨ B) = A

De Morgan’s Theorem
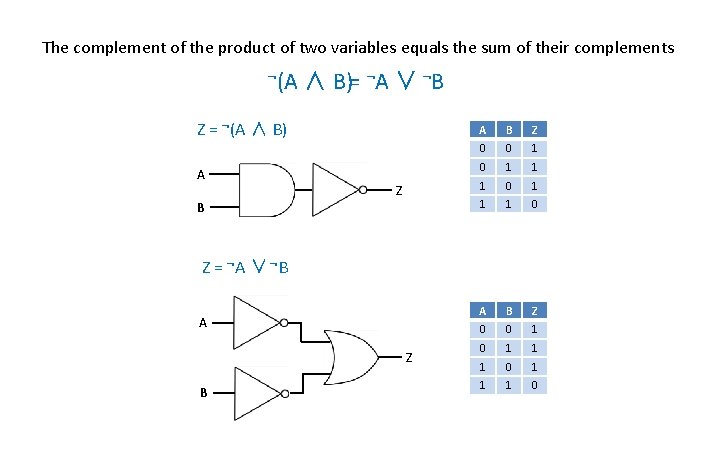
The complement of the product of two variables equals the sum of their complements ¬(A ∧ B)= ¬A ∨ ¬B Z = ¬(A ∧ B) A Z B A B Z 0 0 1 0 1 1 1 0 Z = ¬A ∨ ¬B A Z B
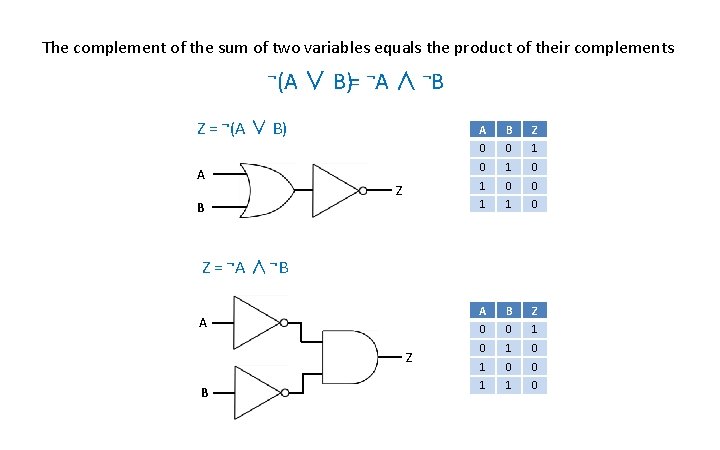
The complement of the sum of two variables equals the product of their complements ¬(A ∨ B)= ¬A ∧ ¬B Z = ¬(A ∨ B) A B Z 0 0 1 0 1 0 0 1 1 0 Z = ¬A ∧ ¬B A Z B

Complement A∧ 0=0 A ∨ ¬A = 1 Associative A∨ 1=1 A ∧ ¬A = 0 Identity Double Negation (A ∨ B) ∨ C = A ∨ (B ∨ C) (A ∧ B) ∧ C = A ∧ (B ∧ C) A∧ 1=A ¬(¬A) = A Annulment Commutative A∨B=B∨A A∧B=B∧A A∨ 0=A Idempotent De Morgan’s Distributive A∨A=A ¬(A ∧ B) = ¬A ∨ ¬B ¬(A ∨ B) = ¬A ∧ ¬B A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) A∧A=A Absorptive A ∨ (A ∧ B) = A A ∧ (A ∨ B) = A
- Slides: 21