Bonferonni correction Adapted from presentation of Experiments in

Bonferonni correction+ Adapted from presentation of Рубанович А. В.

Experiments in finding people with paranormal powers: Joseph Rhine (1950) 1000 people guessed the sequence of 10 cards: red or black? 12 persons guessed 9 of 10 cards, two of them all 10 cards All these “physics” in further experiments did’t confirm their paranormal abilities



Problems of «multiple comparisons» ? q Genome-wide association: gene expression studies with DNA chips – 500 000 SNP. For the significance 0. 01 we can large expect probability up to 5000 falseto Multiple testing islevel dangerous: associations find false association! q Meta-studies: joining and comparison of different results obtained by different authors
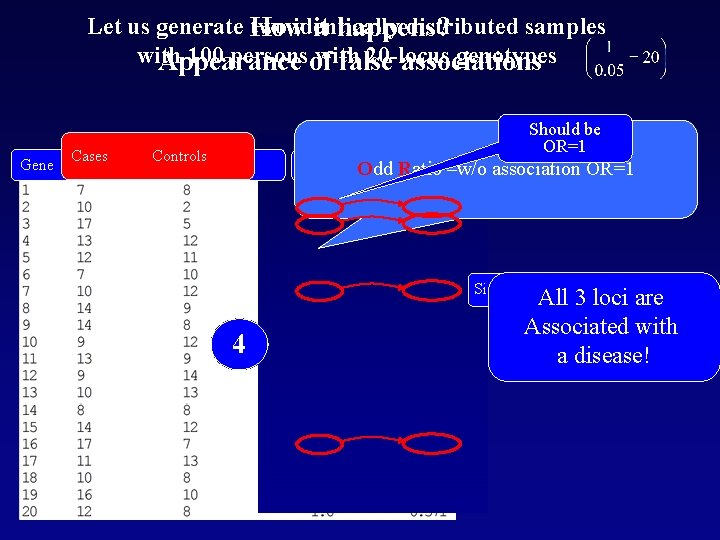
Let us generate How two identically distributed samples it happens? with 100 personsof with 20 -locus genotypes Appearance false associations Gene Cases Sample 1 Should be OR=1 Controls Sample 2 OR p –w/o association OR=1 Odd Ratio Significant! 4123 All 3 loci are Associated with a disease!

How to avoid false associations? Applying m independent statistical tests with significance level a, a probability of at least one false association should be 1 -(1 -a)m < 0. 05 Carlo Bonferroni (1935): When applying m independent statistical test, only significant results are results with

Bonferroni correction kills the significance of certain results: Two mutations associated with the disease Control (100) Cases (100) OR p Mutation 1 1 8 8, 61 0, 044 Mutation 2 5 15 3, 35 0, 024 But adjusted by Bonferroni it should be: p < 0, 05/2=0, 025 1 against 8 with equal size samples :

Example to compute OR case_mut 1=matrix(1, 8, 1) case_non_mut 1=matrix(0, 92, 1) control_mut 1=matrix(1, 1, 1) control_non_mut 1=matrix(0, 99, 1) data=rbind(case_mut 1, case_non_mut 1, control_non_mut 1) res=rbind(matrix(1, 100, 1), matrix(0, 100, 1)) mylogit<- glm(as. formula(res~data), family=binomial(link="logit"), na. action=na. pass) exp(mylogit$coefficients[2]) summary(mylogit)[["coefficients"]][, "Pr(>|z|)"] case_mut 1=matrix(1, 15, 1) case_non_mut 1=matrix(0, 85, 1) control_mut 1=matrix(1, 5, 1) control_non_mut 1=matrix(0, 95, 1) data=rbind(case_mut 1, case_non_mut 1, control_non_mut 1) res=rbind(matrix(1, 100, 1), matrix(0, 100, 1)) mylogit<- glm(as. formula(res~data), family=binomial(link="logit"), na. action=na. pass) exp(mylogit$coefficients[2]) summary(mylogit)[["coefficients"]][, "Pr(>|z|)"]

Assessment of individual sensitivity to ionizing radiation and DNA repair efficiency in a healthy population F. Marcona, C. Andreoli, et al. Mut. Res. , 541 (2003) Not significant! According to Bonferroni shoud be: Genotypes

High-Throughput Detection of GST Polymorphic Alleles in a Pediatric Cancer Population P. Barnette, R. Scholl, et al. Cancer Epidemiology, Biomarkers & Prevention. Vol. 13, 304– 313, 2004 Control 13 genotypes OR=6, 4 P=0, 007 8 diseases Homozygocity in GST prevents cancer! OR=2, 3 P=0, 018 Not significant! Bonferroni correction requests:

Bonferroni method creates more problems than it solves (Thomas Perneger, 1998): q Bonferroni correction leads to very high probability to miss proper association! “Bonferroni adjustments are, at best, unnecessary and, at worst, deleterious to sound statistical inference…”

Errors by statistical testing Null hypothesis – usually about absence of differences in two … and is not taking care about samples the possibility to miss discovery (Type II Error) Type I Error a biologist is trying to Probability to Traditionally reject null hypothesis=probability to avoid find Typethere I error, differences where are i. e. anyto= guarantee avoidance of False discoveries Probability of false discovery Type II Error Probability to accept wrong null hypothesis = Probability not to find existing differences = Probability to miss proper discovery Test power = 1 - Type II error = Probability to reject correctly null hypothesis = Probability to make a discovery

Dependence of Type II error on number of tests using the Bonferroni correction Probability to miss gene with OR=2. 7 with sample sizes 100 (case) and 100 (control) Type II error With 100 comparisons to guarantee avoidance of 1 false discovery, we miss 88% proper discoveries! For m=100 the probability of error is 0. 88 In single test a 5 probability to we miss 50% With comparisons of isdiscoveries miss the discovery 0. 2 1 Number of tests

New algorithm to test statistical hypothesis: FDR-control False Discovery Rate control: Benjamini, Hochberg (1995)) Probability of false discovery < Significance level Type I Error < 0. 05 Traditional principle is replaced by >105 papers in Average fraction of false discoveries < Significance level chosen

Algorithm of FDR control (Benjamini, Hochberg, 1995) q q Order tests according to p-value : p 1 < p 2 < … < pm. Order number oflevel Significance For FDR control on α level ( e. g. 0. 05) , gene P-value for j-th test required we find (gene) Total number of tests Differences are assumed to be significant(genes) for j = 1, …, j*. For j > j* differences are assumed not to be significant

Example: multiple comparisons on 10 tests Test pi 1 0, 001 2 0, 0055 3 4 5 6 7 8 9 10 Order tests FDR in ascending Bonferroni of p-value Significant Correction ordercorrections 0, 005 after FDR control 0, 005 0, 010 0, 005 0, 01 In first cell Bonferonni Bonferroni p-value 0, 005 0, 020 correction 0, 015 In second leaves only first value 0, 005 0, 02 two times larger Three times larger 0, 005 0, 030 0, 04 and so on …. Significant p-values 0, 005 0, 035 0, 3 without correction That’s 0, 040 it!!! 0, 5 For 6 th 0, 005 test 0, 005 0, 045 0, 6 is larger p-value than FDR 0, 8 0, 005 0, 050
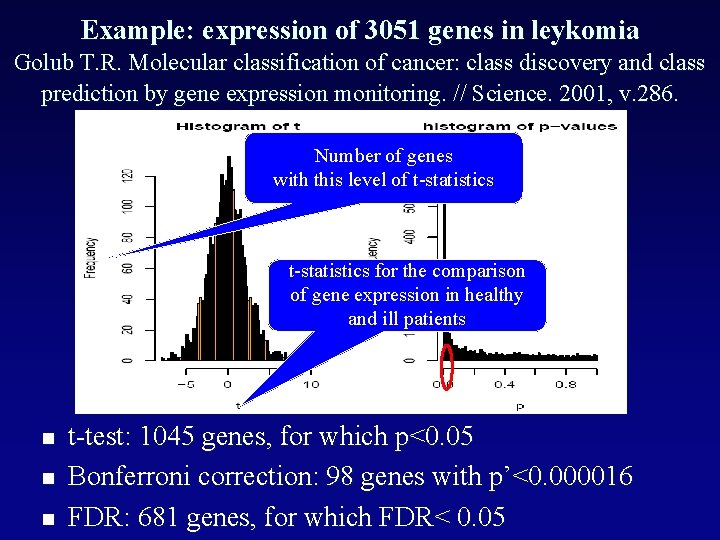
Example: expression of 3051 genes in leykomia Golub T. R. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. // Science. 2001, v. 286. Number of genes with this level of t-statistics for the comparison of gene expression in healthy and ill patients n n n t-test: 1045 genes, for which p<0. 05 Bonferroni correction: 98 genes with p’<0. 000016 FDR: 681 genes, for which FDR< 0. 05
- Slides: 18