Bonding in Solids Melting point K Molecular crystals

Bonding in Solids Melting point (K) Molecular crystals Metals Ionic crystals W(3683) C(<3500) BN(3270) 3000 Mo(2883) Pt(2034) Fe(1808) 2000 1000 0 Covalent crystals organic crystals Cu(1336) Al(933) Pb(600) Na(371) Hg(234) Si. O 2(2001) Li. F(1143) KCl(1063) Si(1683) Ge(1240)

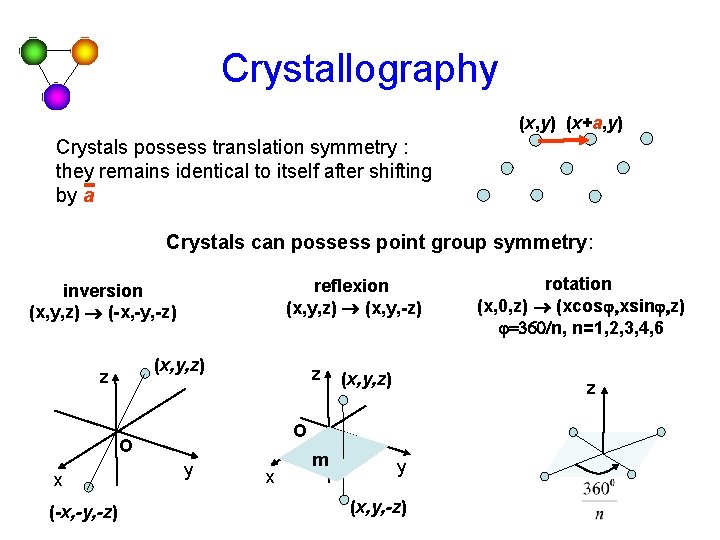
Crystallography (x, y) (x+a, y) Crystals possess translation symmetry : they remains identical to itself after shifting by a Crystals can possess point group symmetry: reflexion (x, y, z) ® (x, y, -z) inversion (x, y, z) ® (-x, -y, -z) (x, y, z) z z (-x, -y, -z) z O O x (x, y, z) y x m rotation (x, 0, z) ® (xcosj, xsinj, z) j=360/n, n=1, 2, 3, 4, 6 y (x, y, -z)

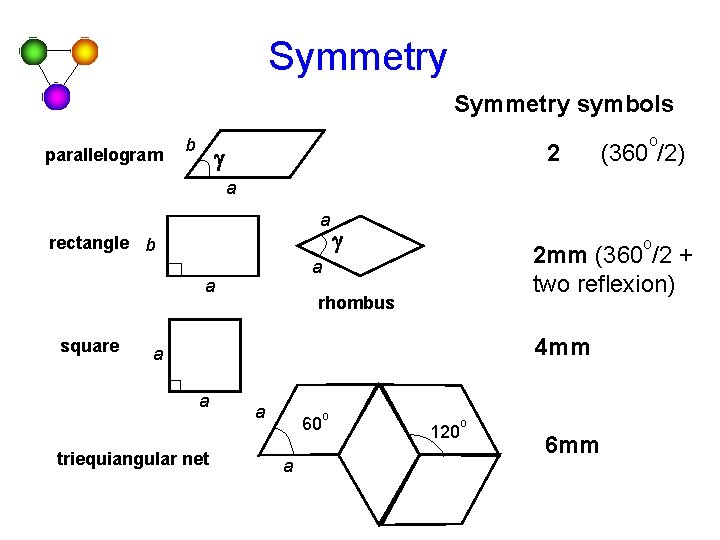
Symmetry symbols parallelogram b 2 g o (360 /2) a a rectangle b o 2 mm (360 /2 + two reflexion) a a square g rhombus 4 mm a a triequiangular net a 60 a o 120 o 6 mm

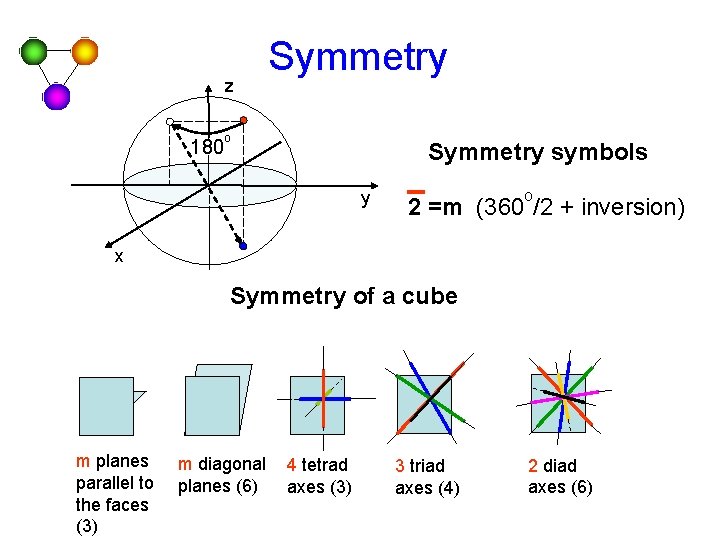
z 180 Symmetry o Symmetry symbols y o 2 =m (360 /2 + inversion) x Symmetry of a cube m planes parallel to the faces (3) m diagonal planes (6) 4 tetrad axes (3) 3 triad axes (4) 2 diad axes (6)

Symmetry There are 32 crystal classes and 230 space groups (see Practical Crystallography). Crystal systems System c b g a a b Axes Min sym o Triclinic (1) a¹b¹c, a¹b¹g¹ 90 Monoclinic (2) a¹b¹c, a=b=90 ¹g Orthrhombic (4) a¹b¹c, a=b=g=90 o Trigonal (1) a=b=c, a=b=g¹ 90 o 3 Tetragonal (2) a=b¹c, a=b=g=90 o 4 Hexagonal (1) a=b¹c, a=b=90 o g=120 Cubic (3) a=b=c, a=b=g=90 o o 1, 1 2, m, 2/m mm, 22 6 o Four-3

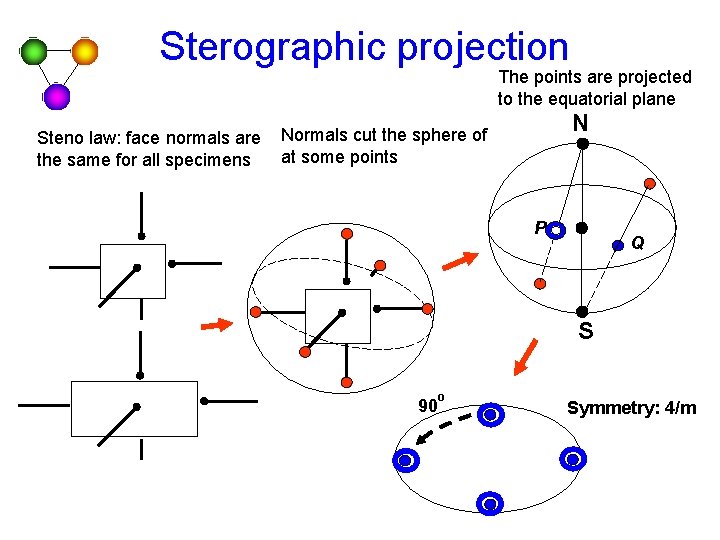
Sterographic projection The points are projected to the equatorial plane Steno law: face normals are the same for all specimens N Normals cut the sphere of at some points P Q S 90 o Symmetry: 4/m

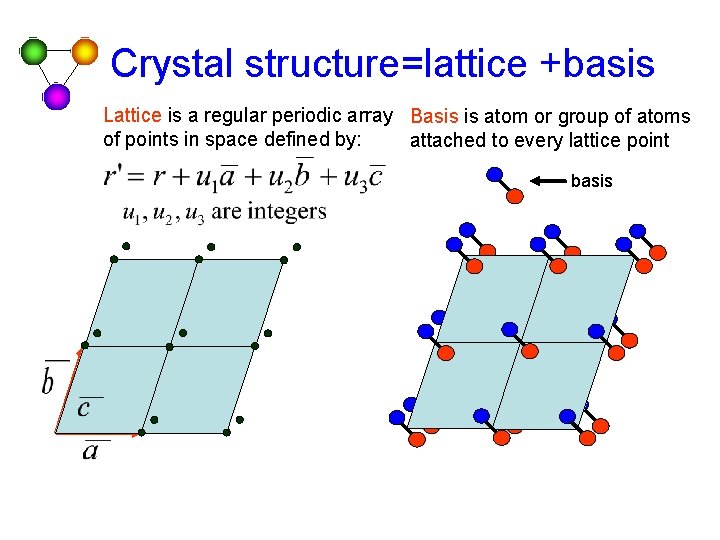
Crystal structure=lattice +basis Lattice is a regular periodic array Basis is atom or group of atoms of points in space defined by: attached to every lattice point basis

Miller Indices [2, 3, 3] 2 Plane intercepts axes at Reciprocal numbers are: Indices of the plane (Miller): (2, 3, 3) 2 Indices of the direction: [2, 3, 3] 3 (200) (111) (100) (110)

Miller Indices Form- set of similar planes resulting from symmetry operation {100} Þ (100), (010), (001), (100), (010), (001) {110} Þ 12 members {111} Þ 6 members [100] (100) Set of dirctions- set of similar directions resulting from symmetry operation <100> Þ [100], [010], [001] <110> Þ 6 members <111> Þ 4 members

Screw axis and glide plane o N-fold screw axes C - combination of rotation 360 /n around C and translation by integer of C/n C C C/2 180 o C/3 120 o 0, C 2 C/3 height 2 -fold axes 3 -fold axes

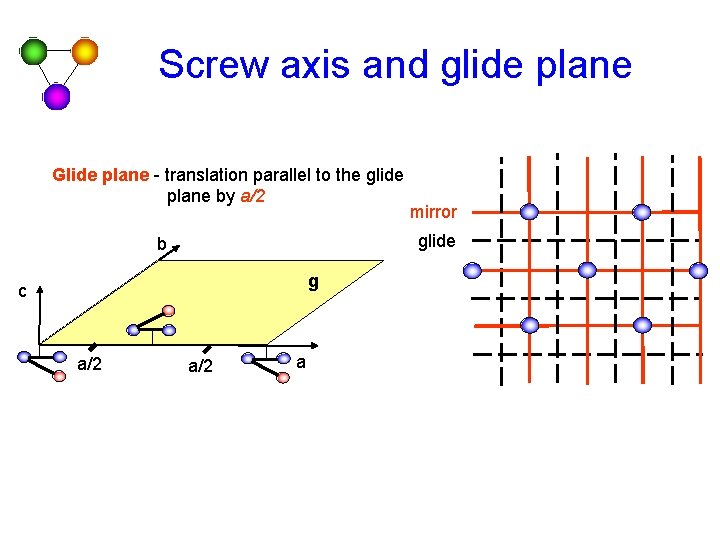
Screw axis and glide plane Glide plane - translation parallel to the glide plane by a/2 glide b g c a/2 mirror a/2 a