Bond Prices and Yields CHAPTER 9 Bond Prices

Bond Prices and Yields CHAPTER 9

Bond Prices and Yields Objectives: 1. Analyze the relationship between bond prices and bond yields. 2. Calculate how bond prices will change over time for a given interest-rate projection. 3. Identify the determinants of bond safety and rating. 4. Analyze how callable, convertible, and sinking fund provisions will affect a bond's equilibrium yield to maturity. 5. Define the yield curve and study its properties

Bond Characteristics n n n n Long-term debt contract Fixed interest payment is paid throughout the life of bond Entire principal payment is paid at maturity date Coupon rate: determines the fixed interest payment Yield to maturity: the average return per year that the investors (or the market) require on the bond if they buy and hold the bond until maturity Coupon rate is fixed, determined by the issuing firm YTM can fluctuate, depending on the investors in the market Zero-coupon bond zero coupon payment ¨ par at maturity date ¨

Treasury Notes and Bonds n n n T Note maturities range up to 10 years T bond maturities range from 10 – 30 years Bid and ask price ¨ Quoted in points and as a percent of par Accrued interest ¨ Quoted price does not include interest accrued Example: if the coupon payments are made on May 1 and Nov 1, you buy a bond on June 11. Assume the price on June 11 is 990, how much you have to pay in order to buy the bond. (assume there are 40 days from May 1 -June 11

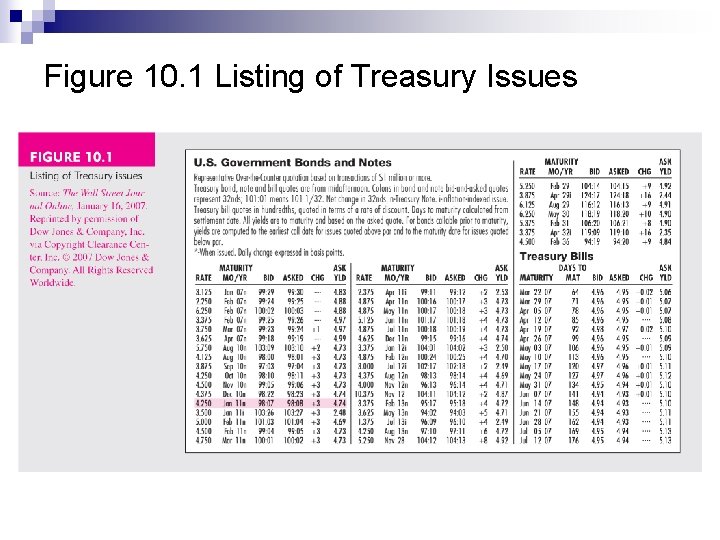
Figure 10. 1 Listing of Treasury Issues

Corporate Bonds n n Most bonds are traded over the counter Registered Bearer bonds Secured and unsecured ¨ Secured: n n ¨ Unsecured n n n Collateral Mortgage Debentures Notes Call provisions: allows issuer to buy back bond before maturity date at a specific call price Why the company wants to call the bond? ¨ Call provision is in favor of the issuer. So if everything else is the same, callable bond would have to give higher yield, higher coupon to investors than regular bonds ¨

Corporate Bonds n Convertible bond: a bond with option allowing the bondholder to exchange the bond for a specific number of shares of common stock in the firm ¨ n When bondholder want to convert bond into stocks? Puttable bond: gives the option to bondholder to either exchange the bond for par value at some date or to extend for a given number of year When bondholders want to exchange for par value before maturity ¨ When bondholders want to extend the bond for a given number of year after maturity ¨ n Floating rate bond ¨ n coupon rate is tied to current market rates Preferred stocks

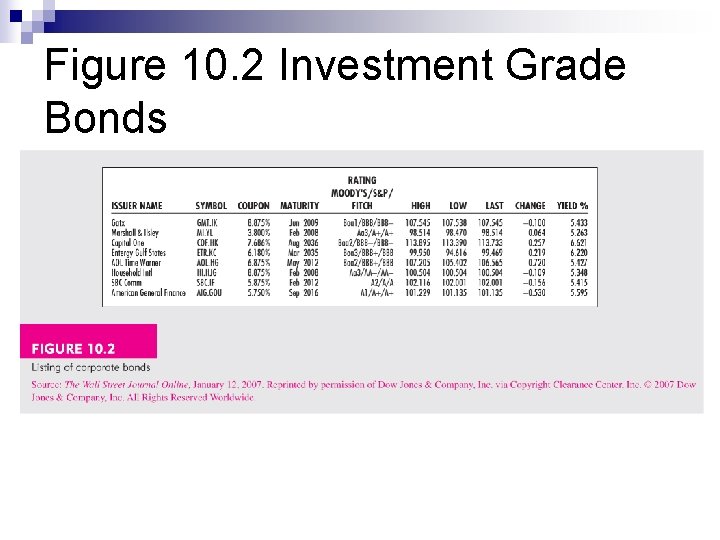
Figure 10. 2 Investment Grade Bonds

Other Domestic Issuers Federal Home Loan Bank Board n Farm Credit Agencies n Ginnie Mae n Fannie Mae n Freddie Mac n

Innovations in the Bond Market n Reverse floaters ¨ n Asset-backed bonds ¨ n backed by assets of the firm Pay-in-kind bonds ¨ n Reverse of floating rate bond issuers may choose to pay interest either in cash or in additional bon Catastrophe bonds issued by insurance company, give high yield ¨ In the event of catastrophe, the obligation to pay interest and principal can be delayed or forgiven ¨ n Indexed bonds ¨ payments are tied to a general price index or price of a particular commodity ¨ TIPS (Treasury Inflation Protected Securities)

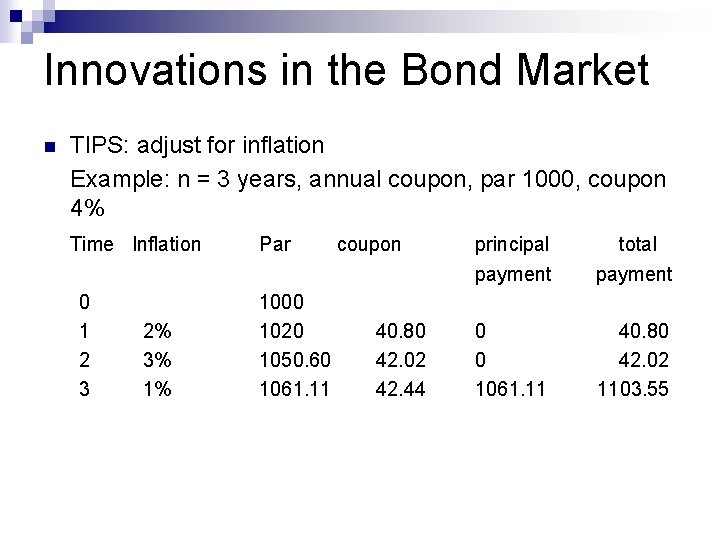
Innovations in the Bond Market n TIPS: adjust for inflation Example: n = 3 years, annual coupon, par 1000, coupon 4% Time Inflation 0 1 2 3 2% 3% 1% Par 1000 1020 1050. 60 1061. 11 coupon 40. 80 42. 02 42. 44 principal payment total payment 0 0 1061. 11 40. 80 42. 02 1103. 55

Bond Pricing T P B = å t =1 Ct T (1+ r ) + Par Value T T (1+ r ) Price of bond = present value of all future coupon payments + present value of the par value PB = Price of the bond Ct = interest or coupon payments T = number of periods to maturity r = semi-annual discount rate or the semi-annual yield to maturity

Example 1) 8% coupon, pay annually, 10 years to maturity, par = 1000, YTM = 6% • Using formula • Using calculator • PMT = 80, FV = 1000, n = 10, I/Y = 6 2) The same information, but the bond is paying interest semiannually. What is the price of the bond?

Yield to Maturity Yield to maturity is a measure of the average rate of return that will be earned if the bond is held to maturity. YTM is the discount rate that makes the present value of a bond’s payments equal to its price YTM is the solution of : n 8% coupon, 30 -year bond selling at $1, 276. 76, what is the yield to maturity?

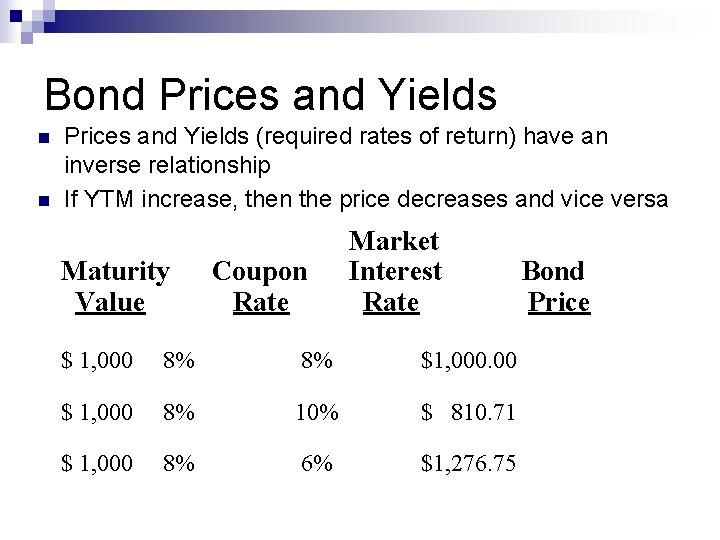
Bond Prices and Yields n n Prices and Yields (required rates of return) have an inverse relationship If YTM increase, then the price decreases and vice versa Maturity Value Coupon Rate Market Interest Rate $ 1, 000 8% 8% $1, 000. 00 $ 1, 000 8% 10% $ 810. 71 $ 1, 000 8% 6% $1, 276. 75 Bond Price

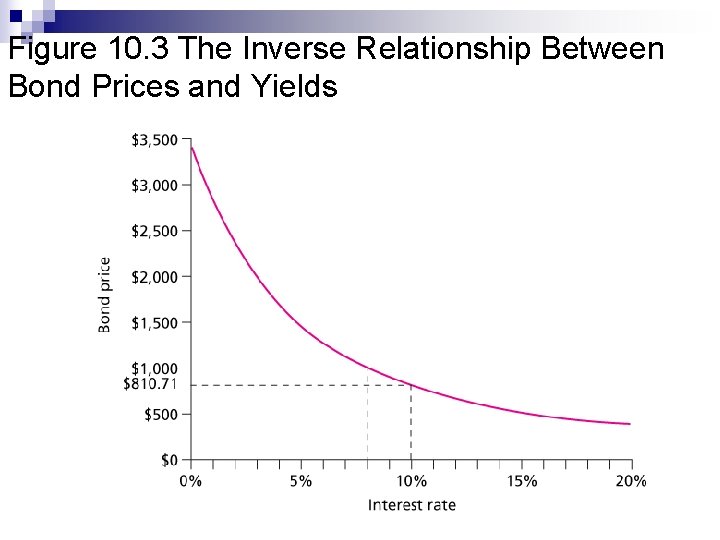
Figure 10. 3 The Inverse Relationship Between Bond Prices and Yields

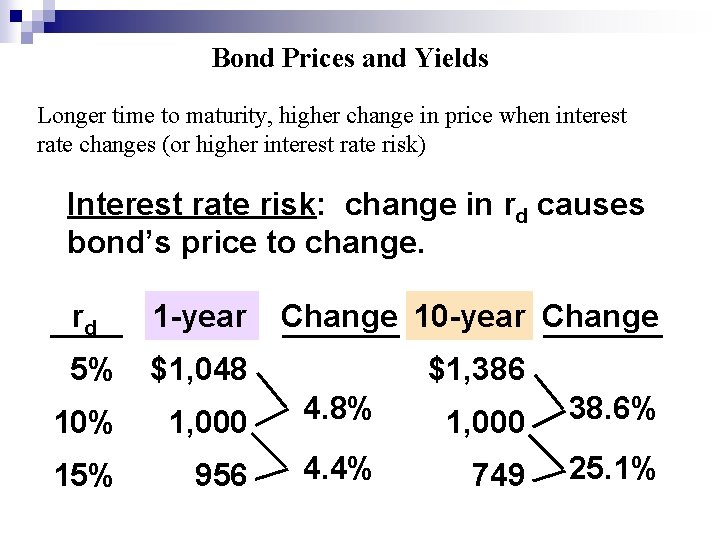
Bond Prices and Yields Longer time to maturity, higher change in price when interest rate changes (or higher interest rate risk) Interest rate risk: change in rd causes bond’s price to change. rd 1 -year Change 10 -year Change 5% $1, 048 $1, 386 10% 1, 000 4. 8% 15% 956 4. 4% 1, 000 38. 6% 749 25. 1%

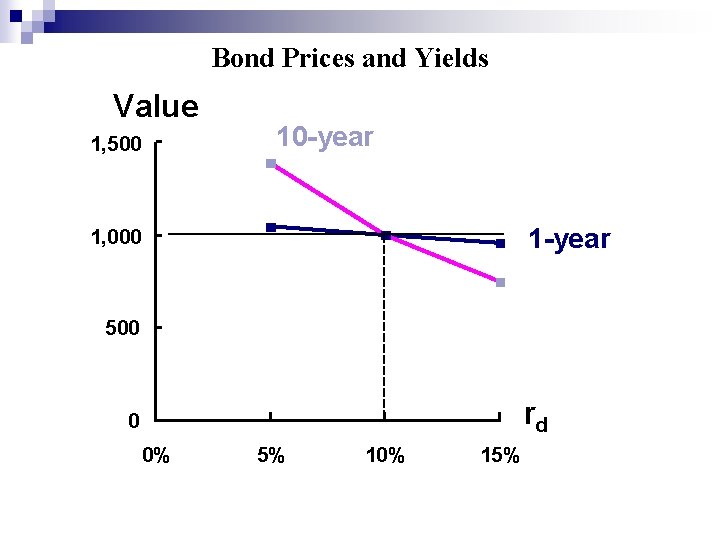
Bond Prices and Yields Value 1, 500 10 -year 1, 000 500 rd 0 0% 5% 10% 15%

Alternative Measures of Yield n Yield to Call ¨ Call price replaces par ¨ Call date replaces maturity ¨ Example: 8% coupon, semi-annual, 30 years to maturity, current price = 1150, callable in 10 years, call price = 1100. What is the yield to call and yield to maturity

Holding Period Return Where Pt = Bond Price at time t Pt+1= Bond Price at time t+1

Definitions Annual coupon pmt Current yield = Current price Capital gains yield = Change in price Beginning price Expected total = return YTM = Expected Curr yld + Expected cap gains yld

Find current yield and capital gains yield for a 9%, 10 -year bond when the bond sells for $887 and YTM = 10. 91%. $90 Current yield = $887 = 0. 1015 = 10. 15%.

YTM = Current yield + Capital gains yield. Cap gains yield = YTM - Current yield = 10. 91% - 10. 15% = 0. 76%. Could also find values in Years 1 and 2, get difference, and divide by value in Year 1. Same answer.

BOND PRICES OVER TIME

Premium and Discount Bonds n n n Premium Bond ¨ price > par ¨ Coupon rate exceeds yield to maturity ¨ Bond price will decline to par over its maturity Discount Bond ¨ price < par ¨ Yield to maturity exceeds coupon rate ¨ Bond price will increase to par over its maturity Bond selling at par price = par ¨ Yield to maturity = coupon rate ¨ bond price is constant throughout the life of bond ¨

BOND PRICES OVER TIME Suppose the bond was issued 20 years ago and now has 10 years to maturity. What would happen to its value over time if the required rate of return or the YTM remained at 10%, or at 13%, or at 7%?

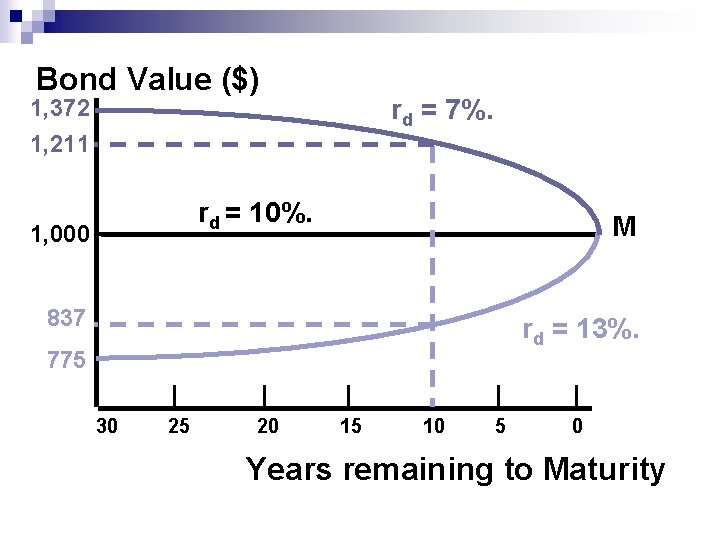
Bond Value ($) rd = 7%. 1, 372 1, 211 rd = 10%. 1, 000 M 837 rd = 13%. 775 30 25 20 15 10 5 0 Years remaining to Maturity

BOND PRICES OVER TIME At maturity, the value of any bond must equal its par value. n The value of a premium bond would decrease to $1, 000. n The value of a discount bond would increase to $1, 000. n A par bond stays at $1, 000 if rd (YTM) remains constant. n

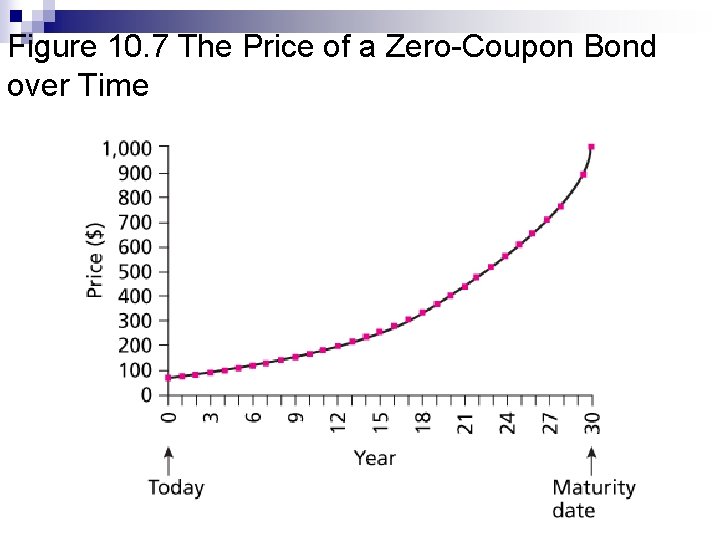
Figure 10. 7 The Price of a Zero-Coupon Bond over Time

DEFAULT RISK AND BOND PRICING

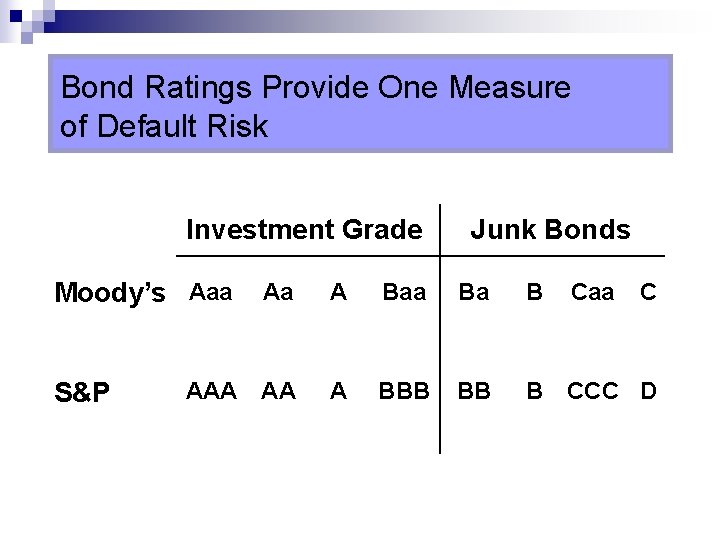
Default Risk and Ratings n Rating companies ¨ Moody’s Investor Service ¨ Standard & Poor’s ¨ Fitch n Rating Categories ¨ Investment grade ¨ Speculative grade

Figure 10. 8 Definitions of Each Bond Rating Class

Bond Ratings Provide One Measure of Default Risk Investment Grade Moody’s Aaa S&P Junk Bonds Aa A Baa Ba B Caa C AAA AA A BBB BB B CCC D

Factors Used by Rating Companies Coverage ratios n Leverage ratios n Liquidity ratios n Profitability ratios n Cash flow to debt n

Protection Against Default n Sinking funds ¨ n Subordination of future debt ¨ n Restrictions on additional borrowing that stipulates that senior bondholders will be paid first in the event of bankruptcy Dividend restrictions ¨ n A bond that calls for the issuer to periodically repurchase some proportion of the outstanding bonds prior to maturity Limit dividend payout to protect bondholders Collateral Uses assets to back up bonds: mortgage bond, collateral trust bond, equipment obligation bond. ¨ Collaterals are secured bonds ¨ Unsecured bond: debentures ¨

THE YIELD CURVE

Term Structure of Interest Rates Relationship between yields to maturity and maturity n Yield curve - a graph of the yields on bonds relative to the number of years to maturity n ¨ Usually Treasury Bonds ¨ Have to be similar risk or other factors would be influencing yields

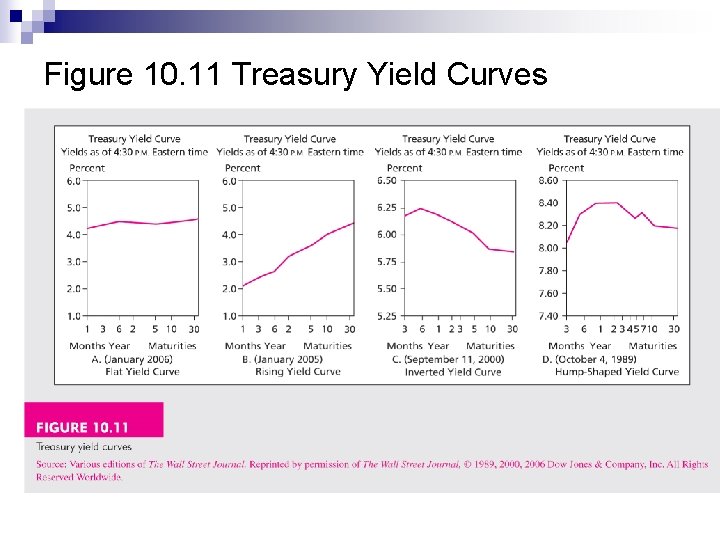
Figure 10. 11 Treasury Yield Curves

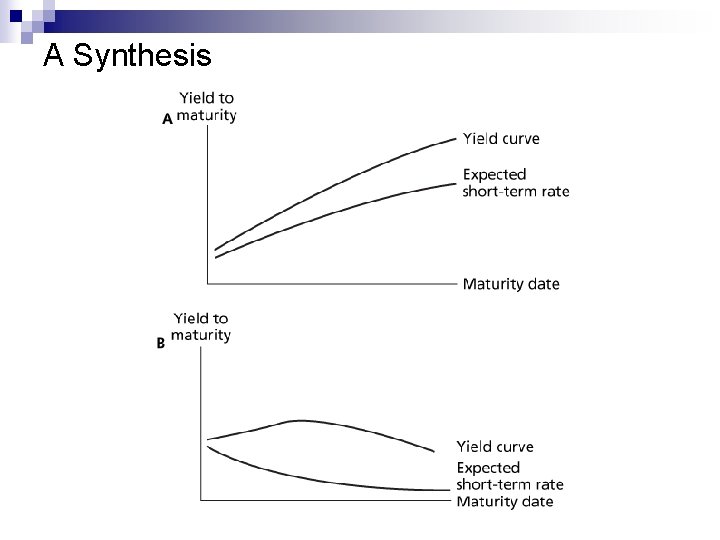
Theories of Term Structure n Expectations ¨ Long term rates are a function of expected future short term rates ¨ Upward slope means that the market is expecting higher future short term rates ¨ Downward slope means that the market is expecting lower future short term rates n Liquidity Preference ¨ Upward bias over expectations ¨ The observed long-term rate includes a risk premium n Combination (Synthesis)

Expectation hypothesis (when short-term interest rate is expected to increase) n n n n Current interest on 1 -year bond = 8% (r 1=8%) Everyone in the market believes that the interest one 1 year bond next year will rise to 10% (E(r 2) = 10%) Investment A: year 1: buy 1 -year bond year 2: buy another 1 -year bond Investment B: year 1: buy 2 -year bond In order for investment B to be competitive with investment A, B has to offer an average annual compound return = average annual compound return of A What is the average annual compound return of B or YTM of the 2 -year bond in B? You will find the YTM of 2 -year bond > YTM of 1 -year bond at time = 0, this is due to E(r 2) > r 1 ( the expected short-term rate increases in the future)

Figure 10. 12 Returns to Two 2 -year Investment Strategies

Expectation hypothesis (when short-term interest rate is expected to decrease) n n n n Current interest on 1 -year bond = 8% (r 1=8%) Everyone in the market believes that the interest one 1 year bond next year will decrease to 6% (E(r 2) = 6%) Investment A: year 1: buy 1 -year bond year 2: buy another 1 -year bond Investment B: year 1: buy 2 -year bond In order for investment B to be competitive with investment A, B has to offer an average annual compound return = average annual compound return of A What is the average annual compound return of B or YTM of the 2 -year bond in B? You will find the YTM of 2 -year bond < YTM of 1 -year bond at time = 0, this is due to E(r 2) < r 1 ( the expected short-term rate decreases in the future)

The Expectation Hypothesis • In practice, we don’t observe directly the expectation of next year’s rate, but we can observe the yields on bonds of different maturities. So from that, using the yields on bonds of different maturities, we can calculate the expected short-term interest rate (or the expected YTM of 1 -year bond) in the future • According to expectation hypothesis, the forward rate = expected short term rate. • Forward rate is the inferred short-term rate of interest for a future period that makes the expected total return of a long-term bond = that of rolling over short-term bonds. Example: Suppose that 1 -year bonds offer yields to maturity of 8%, and 2 -year bonds have yields of 8. 995%. What is the expected one-period rate or forward rate for the third year?

Forward Rates Implied in the Yield Curve (1+ y n ) (1. 07 ) 3 n = (1+ y n -1) (1+ f n ) n -1 2 = (1. 06) (1. 0902 ) Example: Suppose that 2 -year bonds offer yields to maturity of 6%, and 3 -year bonds have yields of 7%. What is the expected one-period rate for the third year? For example, using a 1 -yr and 2 -yr rates Longer term rate, y(n) = 7% Shorter term rate, y(n-1) = 6% Forward rate, a one-year rate in one year = 9. 02%

Liquidity preference theory n n According to expectation theory, long-term yield depends on expected short-term yield. If expected short-term increases, then long-term increases, and vice versa This theory does not take into account risk. Risk of long-term > risk of short-term Liquidity preference theory: investors demand of risk premium (liquidity premium) for holding long-term bonds ¨ fn = E(rn) + Liquidity premium ¨ Forward rate in year n = expected short-term rate in year n + liquidity premium ¨ Predict upward sloping yield curve even in the case of expected short-term rates are unchanged. ¨

Liquidity preference theory n n n Suppose the short-term rate of interest rate is currently 8%, and investors expect it to remain at 8% next year. In the absence of liquidity premium, with no expectation of a change in yields, the YTM on two-year bonds would be 8% (according to expectation hypothesis), and the yield curve would be flat, the forward rate would be 8% However, what if investors demand a risk premium to invest in two-year rather than one-year bonds? If the liquidity premium = 1%, then according to liquidity theory, the forward rate would be = 8%+1% = 9% and the YTM of two-year bond would be (1+y 2)2 = 1. 08× 1. 09 = 1. 7772 therefore y 2=0. 085 = 8. 5% n YTM of 2 -year bond (8. 5%) > YTM of 1 -year bond (8%) solely due to the liquidity premium.

A Synthesis

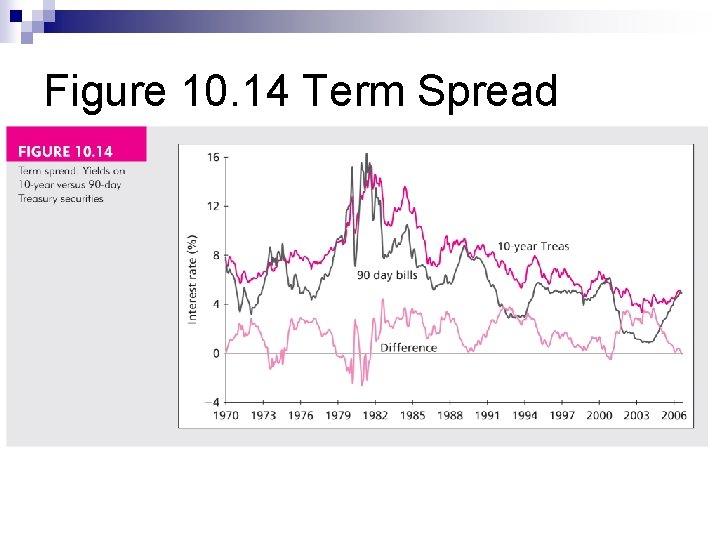
Figure 10. 14 Term Spread

Summary • Inverse relationship between bond prices and bond yields • Premium and discount bonds • Corporate bonds and default risk • Term structure of interest rates Expectations theory Liquidity preference theory Synthesis • Next Class: Managing Bond Portfolios