Bond Prices and Yields CHAPTER 14 BOND CHARACTERISTICS

Bond Prices and Yields CHAPTER 14

BOND CHARACTERISTICS Face or par value Coupon rate Zero coupon bond Compounding and payments Accrued Interest Indenture BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 2

DIFFERENT ISSUERS OF BONDS U. S. Treasury Notes and Bonds Corporations Municipalities International Governments and Corporations Innovative Bonds Floaters and Inverse Floaters Asset-Backed Catastrophe BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 3

FIGURE 14. 1 LISTING OF TREASURY ISSUES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 4
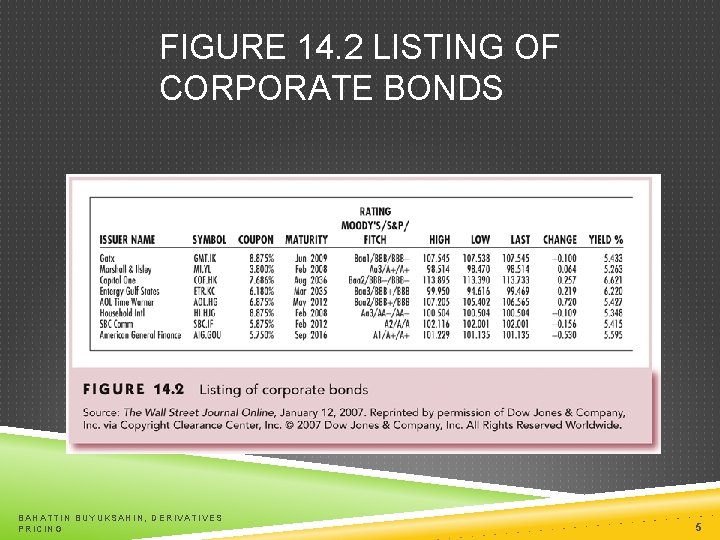
FIGURE 14. 2 LISTING OF CORPORATE BONDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 5

PROVISIONS OF BONDS Secured or unsecured Call provision Convertible provision Put provision (putable bonds) Floating rate bonds Preferred Stock BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 6

CONVERTIBLE BONDS Give bondholders an option to exchange each bond for a specified nb of shares of common stock Conversion ratio = number of shares per convertible bond Market conversion value = conversion ratio * current market value per share Conversion premium = bond value - conversion value intuitively: extra amount to pay so as to become a shareholder BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 7

CONVERSION EXAMPLE BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 8

CONVERSION EXAMPLE BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 9

INNOVATION IN THE BOND MARKET Inverse Floaters Asset-Backed Bonds Catastrophe Bonds Indexed Bonds BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 10
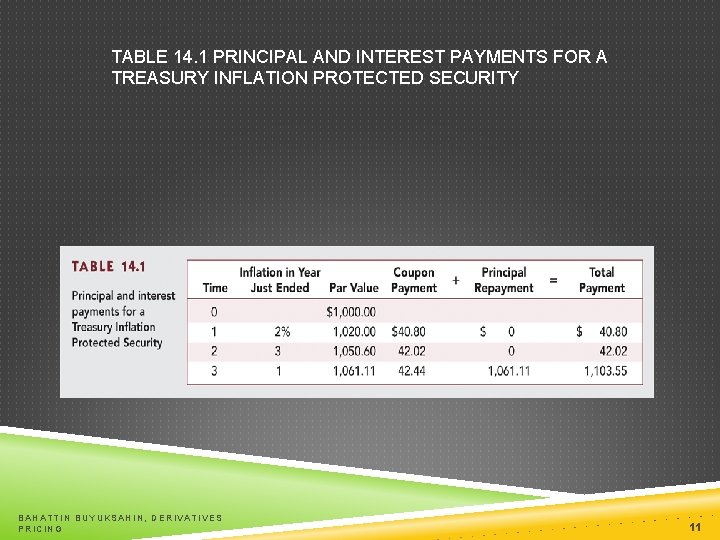
TABLE 14. 1 PRINCIPAL AND INTEREST PAYMENTS FOR A TREASURY INFLATION PROTECTED SECURITY BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 11

BOND PRICES AND YIELDS Time value of money and bond pricing Time to maturity and risk Yield to maturity vs. yield to call vs. realized compound yield Determinants of YTM risk, maturity, holding period, etc. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 12

BOND PRICING PB = Price of the bond Ct = interest or coupon payments T = number of periods to maturity y = semi-annual discount rate or the semiannual yield to maturity BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 13

PRICE: 10 -YR, 8% COUPON, FACE = $1, 000 Ct P T r = 40 (SA) = 1000 = 20 periods = 3% (SA) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 14

BOND PRICING Equation: P = PV(annuity) + PV(final payment) = Example: Ct = $40; Par = $1, 000; disc. rate = 4%; T=60 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 15

BOND PRICES AND YIELDS Prices and Yields (required rates of return) have an inverse relationship When yields get very high the value of the bond will be very low When yields approach zero, the value of the bond approaches the sum of the cash flows BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 16

PRICES VS. YIELDS P yield intuition convexity Fig 14. 3 intuition: yield P price impact BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 17
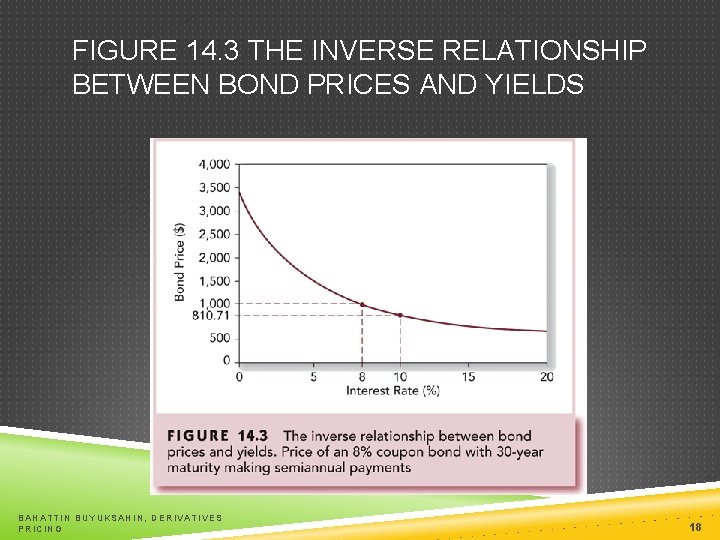
FIGURE 14. 3 THE INVERSE RELATIONSHIP BETWEEN BOND PRICES AND YIELDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 18
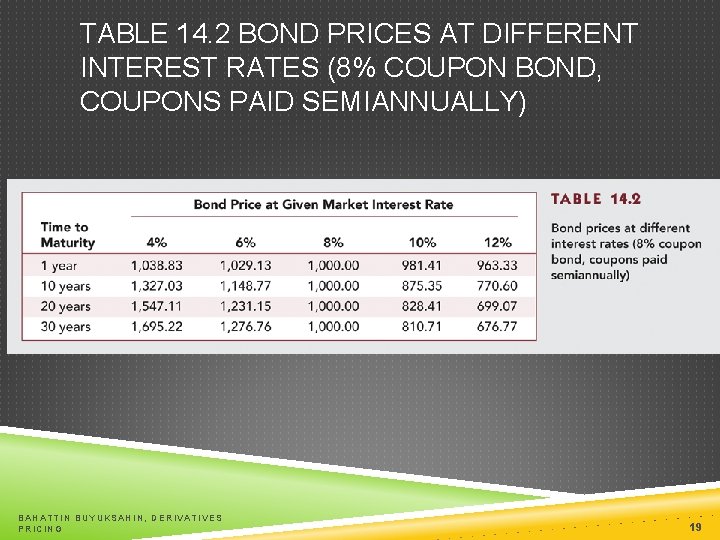
TABLE 14. 2 BOND PRICES AT DIFFERENT INTEREST RATES (8% COUPON BOND, COUPONS PAID SEMIANNUALLY) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 19

YIELD TO MATURITY Interest rate that makes the present value of the bond’s payments equal to its price Solve the bond formula for r BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 20

YIELD TO MATURITY EXAMPLE 10 yr Maturity Coupon Rate = 7% Price = $950 Solve for r = semiannual rate BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING r = 3. 8635% 21

YIELD MEASURES Bond Equivalent Yield 7. 72% = 3. 86% x 2 Effective Annual Yield (1. 0386)2 - 1 = 7. 88% Current Yield Annual Interest / Market Price $70 / $950 = 7. 37 % Yield to Call BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 22

PURE DISCOUNT BONDS (ZEROCOUPON BONDS) A zero rate (or spot rate), for maturity T is the rate of interest earned on an investment that provides a payoff only at time T Discount bonds, also called zero-coupon bonds, are securities which “make a single payment at a date in the future known as maturity date. The size of this payment is the face value of the bond. The length of time to the maturity date is the maturity of the bond” (Campbell, Lo, Mac. Kinley (1996)). BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 23

PURE DISCOUNT BOND The promised cash payment on a pure discount bond is called its face value or par value. Yield (interest rate) on a pure discount bond is the annualized rate of return to investors who buy it and hold it until it matures. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 24
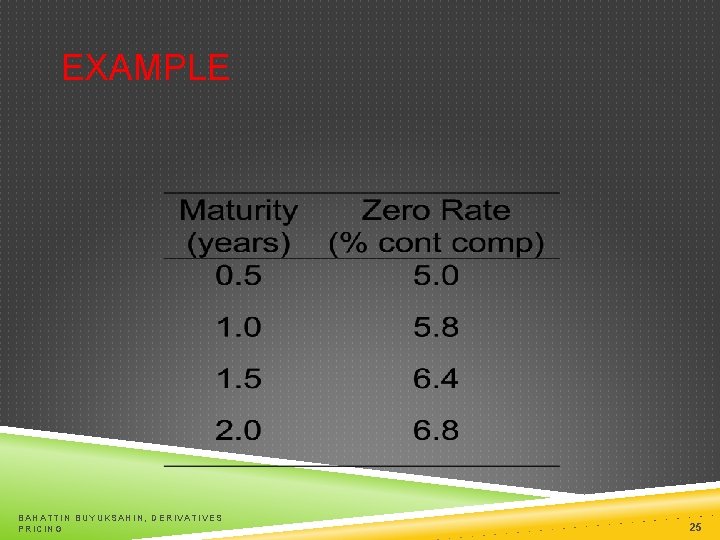
EXAMPLE BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 25

BOND PRICING To calculate the cash price of a bond we discount each cash flow at the appropriate zero rate The theoretical price of a two-year bond providing a 6% coupon semiannually is BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 26

BOND YIELD The bond yield is the discount rate that makes the present value of the cash flows on the bond equal to the market price of the bond Suppose that the market price of the bond in our example equals its theoretical price of 98. 39 The bond yield is given by solving to get y = 0. 0676 or 6. 76%. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 27

PAR YIELD The par yield for a certain maturity is the coupon rate that causes the bond price to equal its face value. In our example we solve BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 28

PAR YIELD (CONTINUED) In general if m is the number of coupon payments per year, d is the present value of $1 received at maturity and A is the present value of an annuity of $1 on each coupon date BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 29

BOOTSTRAP METHOD TO CALCULATE DISCOUNT FACTOR A discount function is a set of discount factors, where each discount factor is just a present value multiplier. For example, d(1. 0) is the present value of $1 dollar received in one year. The key idea is that each d(x) can be solved as one variable under one equation because we already solved for shorter-term discount factors. The most popular approach is to use bootstrap method BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 30
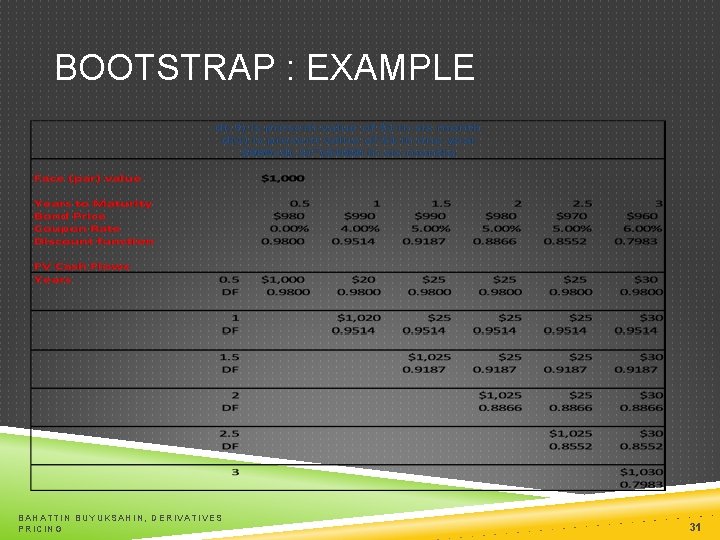
BOOTSTRAP : EXAMPLE BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 31
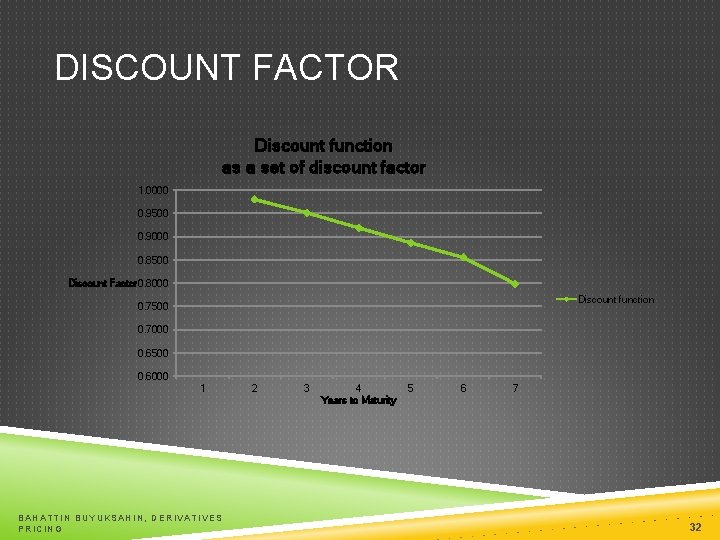
DISCOUNT FACTOR Discount function as a set of discount factor 1. 0000 0. 9500 0. 9000 0. 8500 Discount Factor 0. 8000 Discount function 0. 7500 0. 7000 0. 6500 0. 6000 1 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 2 3 4 Years to Maturity 5 6 7 32

DETERMINING TREASURY ZERO RATES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 33
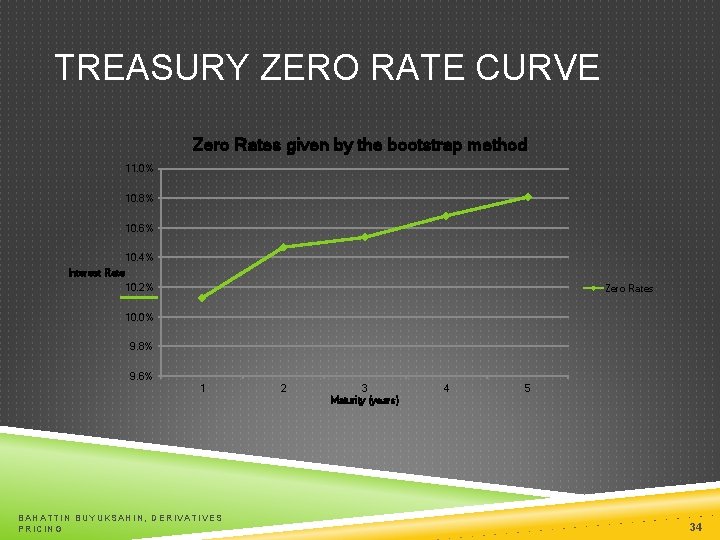
TREASURY ZERO RATE CURVE Zero Rates given by the bootstrap method 11. 0% 10. 8% 10. 6% 10. 4% Interest Rate 10. 2% Zero Rates 10. 0% 9. 8% 9. 6% 1 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 2 3 Maturity (years) 4 5 34
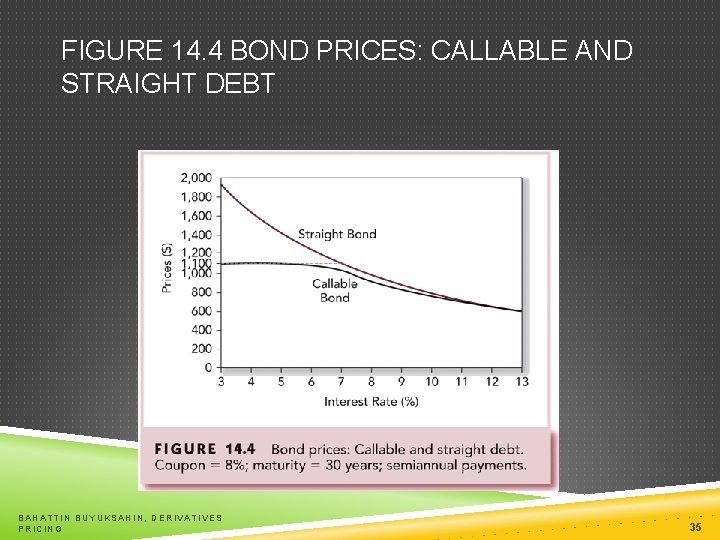
FIGURE 14. 4 BOND PRICES: CALLABLE AND STRAIGHT DEBT BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 35

EXAMPLE 14. 4 YIELD TO CALL BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 36

REALIZED YIELD VERSUS YTM Reinvestment Assumptions Holding Period Return Changes in rates affect returns Reinvestment of coupon payments Change in price of the bond BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 37
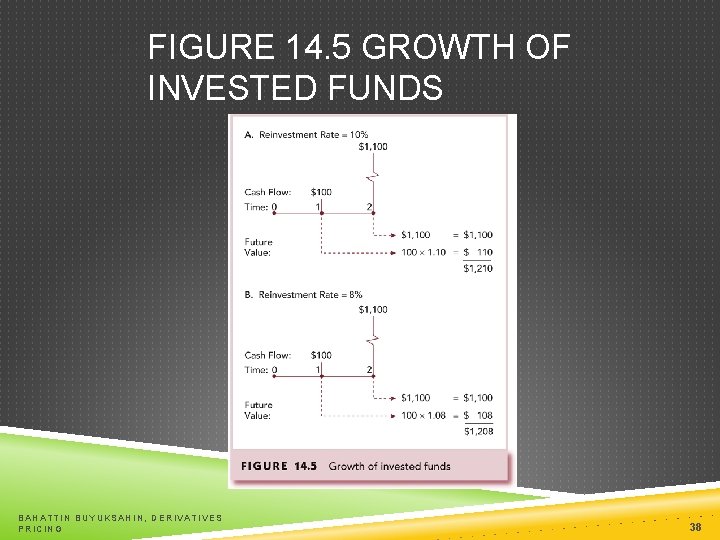
FIGURE 14. 5 GROWTH OF INVESTED FUNDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 38
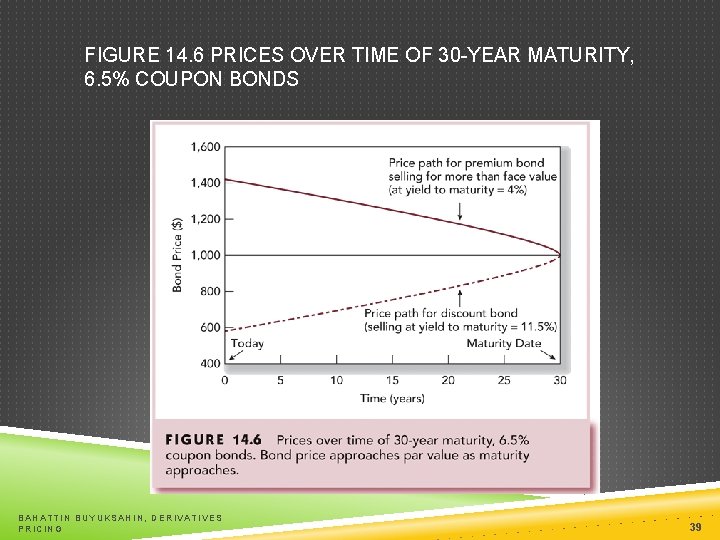
FIGURE 14. 6 PRICES OVER TIME OF 30 -YEAR MATURITY, 6. 5% COUPON BONDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 39

HOLDING-PERIOD RETURN: SINGLE PERIOD HPR = [ I + ( P 0 - P 1 )] / P 0 where I = interest payment P 1 = price in one period P 0 = purchase price BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 40

HOLDING-PERIOD RETURN EXAMPLE CR = 8% YTM = 8% N=10 years Semiannual Compounding. P 0 = $1000 In six months the rate falls to 7% P 1 = $1068. 55 HPR = [40 + ( 1068. 55 - 1000)] / 1000 HPR = 10. 85% (semiannual) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 41
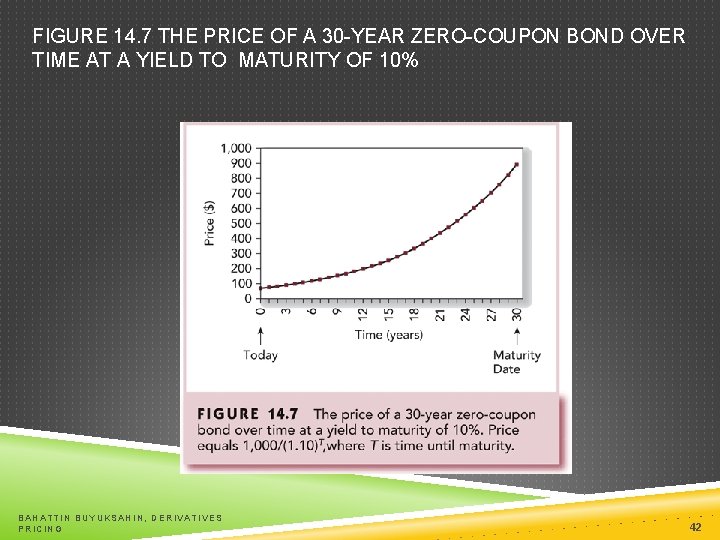
FIGURE 14. 7 THE PRICE OF A 30 -YEAR ZERO-COUPON BOND OVER TIME AT A YIELD TO MATURITY OF 10% BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 42

DEFAULT RISK AND RATINGS Rating companies Moody’s Investor Service Standard & Poor’s Fitch Rating Categories Investment grade Speculative grade/Junk Bonds BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 43
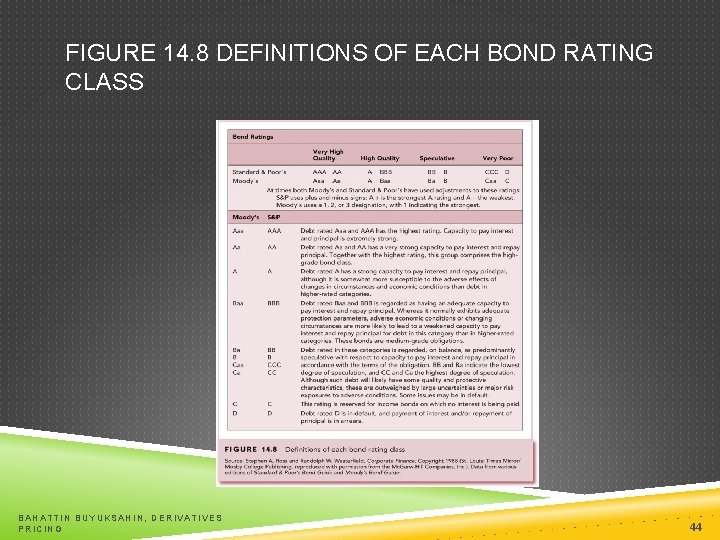
FIGURE 14. 8 DEFINITIONS OF EACH BOND RATING CLASS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 44

FACTORS USED BY RATING COMPANIES Coverage ratios Leverage ratios Liquidity ratios Profitability ratios Cash flow to debt BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 45

TABLE 14. 3 FINANCIAL RATIOS AND DEFAULT RISK BY RATING CLASS, LONGTERM DEBT BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 46
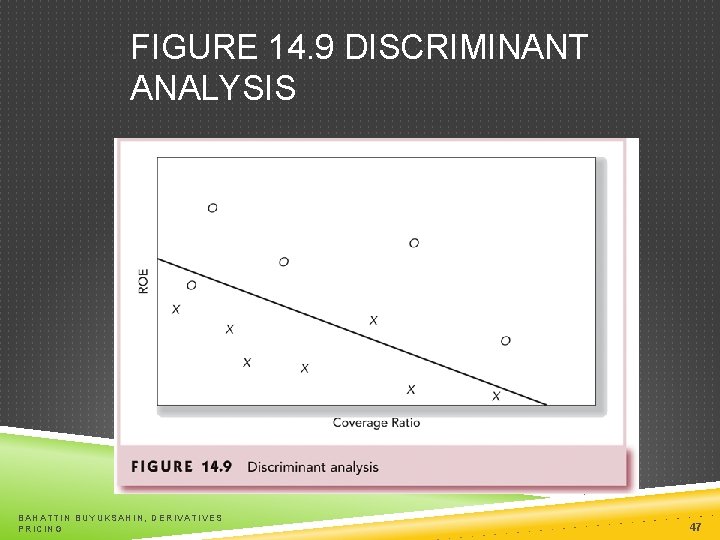
FIGURE 14. 9 DISCRIMINANT ANALYSIS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 47

PROTECTION AGAINST DEFAULT Sinking funds Subordination of future debt Dividend restrictions Collateral BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 48

FIGURE 14. 10 CALLABLE BOND ISSUED BY MOBIL BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 49

DEFAULT RISK AND YIELD Risk structure of interest rates Default premiums Yields compared to ratings Yield spreads over business cycles BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 50
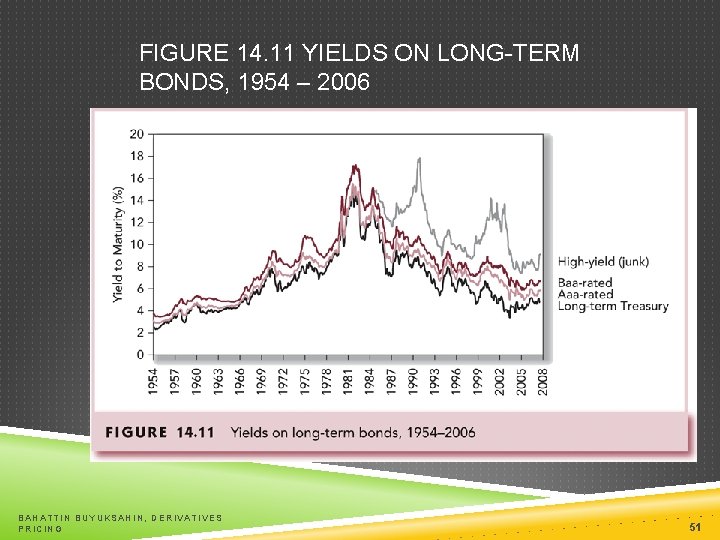
FIGURE 14. 11 YIELDS ON LONG-TERM BONDS, 1954 – 2006 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 51

CREDIT RISK AND COLLATERALIZED DEBT OBLIGATIONS (CDOS) Major mechanism to reallocate credit risk in the fixed-income markets Structured Investment Vehicle (SIV) often used to create the CDO Mortgage-backed CDOs were an investment disaster in 2007 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 52

FIGURE 14. 12 COLLATERALIZED DEBT OBLIGATIONS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 53

CHAPTER 15 The Term Structure of Interest Rates BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 54

OVERVIEW OF TERM STRUCTURE Information on expected future short term rates can be implied from the yield curve The yield curve is a graph that displays the relationship between yield and maturity Three major theories are proposed to explain the observed yield curve BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 55
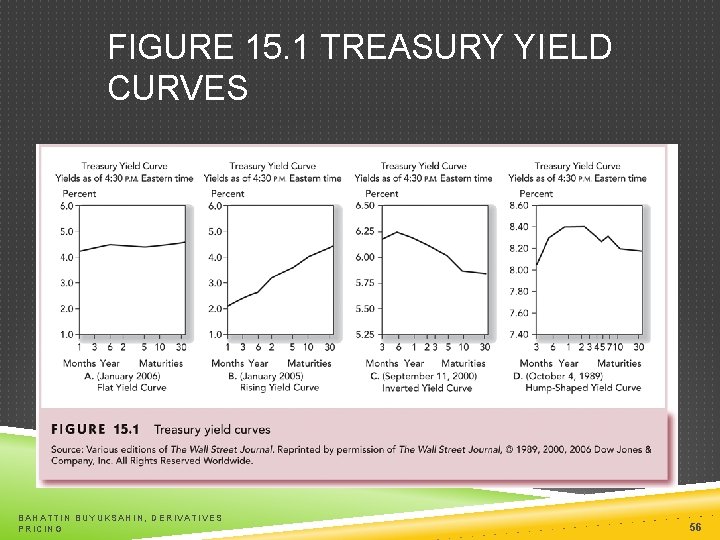
FIGURE 15. 1 TREASURY YIELD CURVES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 56

BOND PRICING Yields on different maturity bonds are not all equal Need to consider each bond cash flow as a stand-alone zero-coupon bond when valuing coupon bonds BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 57
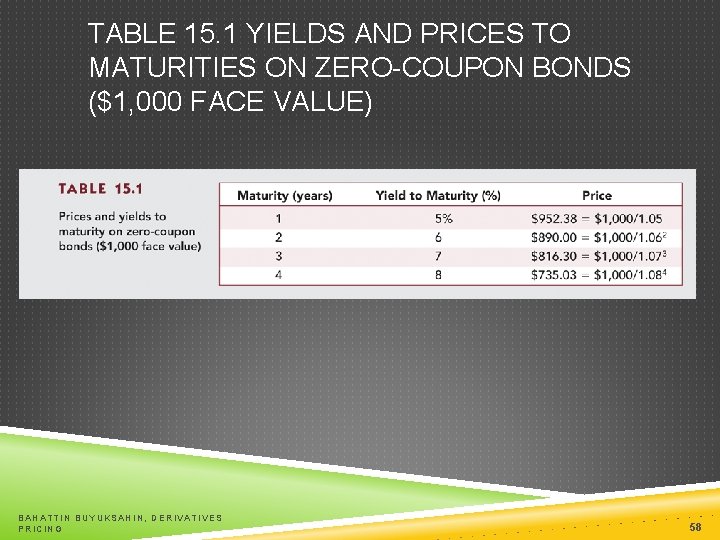
TABLE 15. 1 YIELDS AND PRICES TO MATURITIES ON ZERO-COUPON BONDS ($1, 000 FACE VALUE) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 58

YIELD CURVE UNDER CERTAINTY An upward sloping yield curve is evidence that short-term rates are going to be higher next year When next year’s short rate is greater than this year’s short rate, the average of the two rates is higher than today’s rate BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 59
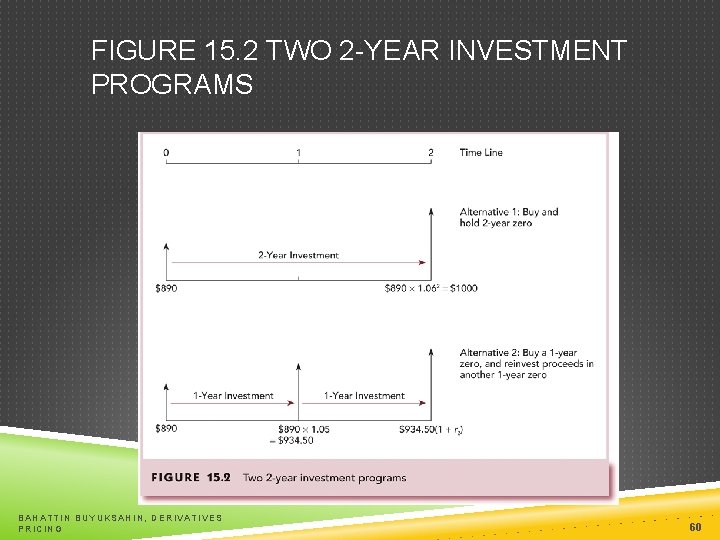
FIGURE 15. 2 TWO 2 -YEAR INVESTMENT PROGRAMS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 60

FIGURE 15. 3 SHORT RATES VERSUS SPOT RATES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 61

FORWARD RATES FROM OBSERVED RATES fn = one-year forward rate for period n yn = yield for a security with a maturity of n BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 62

EXAMPLE 15. 4 FORWARD RATES 4 yr = 8. 00% 3 yr = 7. 00% fn = ? (1. 08)4 = (1. 07)3 (1+fn) (1. 3605) / (1. 2250) = (1+fn) fn =. 1106 or 11. 06% BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 63

DOWNWARD SLOPING SPOT YIELD CURVE EXAMPLE Zero-Coupon Rates Bond Maturity 12% 1 11. 75% 2 11. 25% 3 10. 00% 4 9. 25% 5 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 64

FORWARD RATES FOR DOWNWARD SLOPING Y C EXAMPLE 1 yr Forward Rates 1 yr [(1. 1175)2 / 1. 12] - 1 = 0. 115006 2 yrs [(1. 1125)3 / (1. 1175)2] - 1 = 0. 102567 3 yrs [(1. 1)4 / (1. 1125)3] - 1 = 0. 063336 4 yrs [(1. 0925)5 / (1. 1)4] - 1 = 0. 063008 BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 65

INTEREST RATE UNCERTAINTY What can we say when future interest rates are not known today Suppose that today’s rate is 5% and the expected short rate for the following year is E(r 2) = 6% then: The rate of return on the 2 -year bond is risky for if next year’s interest rate turns out to be above expectations, the price will lower and vice versa BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 66

INTEREST RATE UNCERTAINTY CONTINUED Investors require a risk premium to hold a longer-term bond This liquidity premium compensates shortterm investors for the uncertainty about future prices BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 67
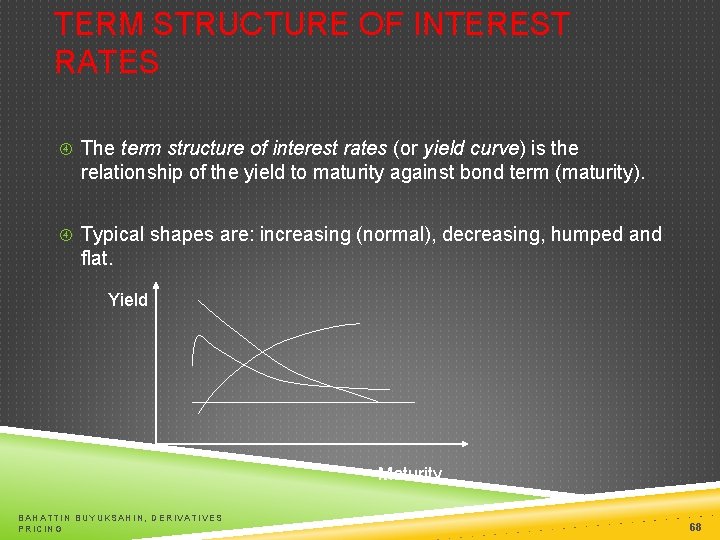
TERM STRUCTURE OF INTEREST RATES The term structure of interest rates (or yield curve) is the relationship of the yield to maturity against bond term (maturity). Typical shapes are: increasing (normal), decreasing, humped and flat. Yield Maturity BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 68

UPWARD VS DOWNWARD SLOPING YIELD CURVE For an upward sloping yield curve: Fwd Rate > Zero Rate > Par Yield For a downward sloping yield curve Par Yield > Zero Rate > Fwd Rate BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 69

THEORIES OF THE TERM STRUCTURE A number of theory have been proposed: Expectation Hypothesis, Liquidity Preference Theory, Preferred Habitats Theory, Segmentation Hypothesis. Fabozzi (1998): Pure Expectation Hypothesis, Liquidity Preference Theory, Preferred Habitats Theory are different forms of the expectation theory ==> two major theories: expectation theory and market segmentation theory. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 70

THEORIES OF THE TERM STRUCTURE OF INTEREST RATES (1) The Pure Expectation Hypothesis: Implied forward rates are unbiased expectations of future spot rates ==> a rising term structure indicate that market expects short-term rates to rise in the future; a flat term structure reflects expectations that the future short term structure will be constant; and so on; Hicks (1937). Problems: It neglects the risks inherent in investing in bonds: if forward rates were perfect predictors of future interest rates then the future prices of bonds will be known with certainty. The Liquidity Preference Theory (Keynes): Given that there is uncertainty, long bonds should have higher returns than short bonds ==> we should expect a risk premium arising out from investors liquidity preferences. It is consistent with the empirical results that yield curves are upward sloping ==> positive risk premium. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 71

THEORIES OF THE TERM STRUCTURE OF INTEREST RATES (2) The Preferred Habitat Theory: It adopts the view that the term structure is composed by two components: Expectations plus risk premium (= liquidity preference theory). However, the risk premium might be negative as well as positive to induce market participants to shift out of their preferred habitat (Modigliani & Sutch (1966)). The Segmentation Hypothesis (Culbertson (1957)): It also recognises that investors have preferred habitat (= preferred habitat theory) ==> individuals have strong maturity preferences ==> there need be no relationship between bonds with different maturities ==> bonds with different maturities are traded in different markets. BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 72

EXPECTATIONS THEORY Observed long-term rate is a function of today’s short-term rate and expected future short-term rates Long-term and short-term securities are perfect substitutes Forward rates that are calculated from the yield on long-term securities are market consensus expected future short-term rates BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 73

LIQUIDITY PREMIUM THEORY Long-term bonds are more risky Investors will demand a premium for the risk associated with long-term bonds The yield curve has an upward bias built into the long-term rates because of the risk premium Forward rates contain a liquidity premium and are not equal to expected future shortterm rates BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 74
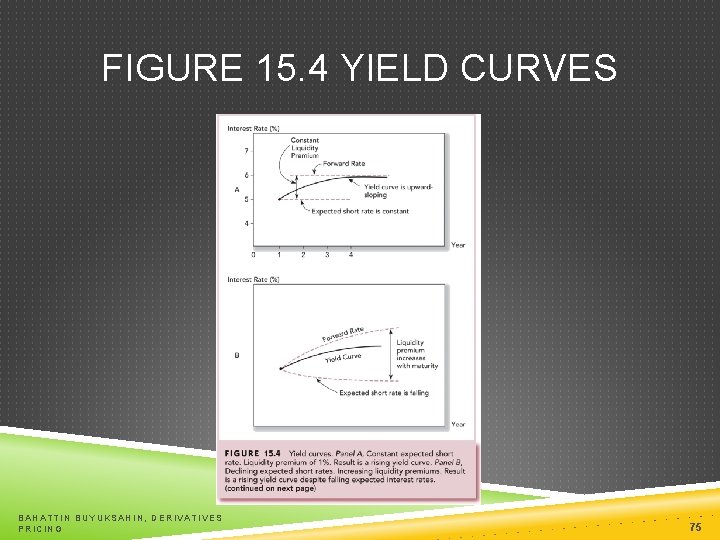
FIGURE 15. 4 YIELD CURVES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 75

FIGURE 15. 4 YIELD CURVES (CONCLUDED) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 76

INTERPRETING THE TERM STRUCTURE If the yield curve is to rise as one moves to longer maturities A longer maturity results in the inclusion of a new forward rate that is higher than the average of the previously observed rates Reason: Higher expectations forward rates or Liquidity premium BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 77
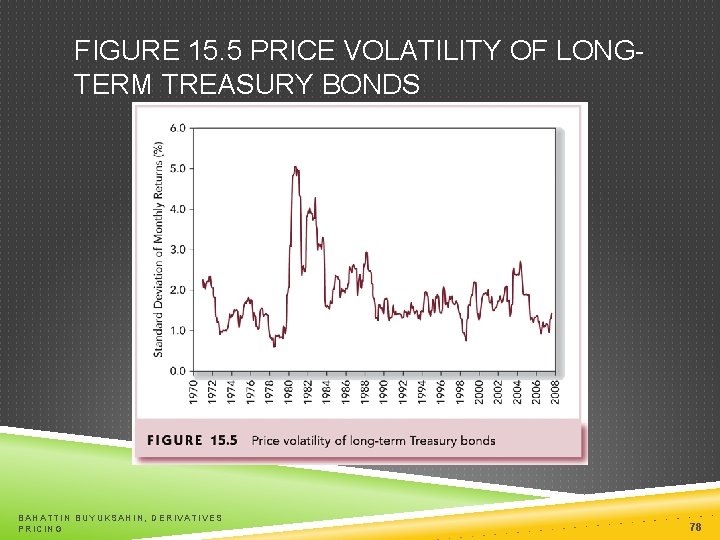
FIGURE 15. 5 PRICE VOLATILITY OF LONGTERM TREASURY BONDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 78
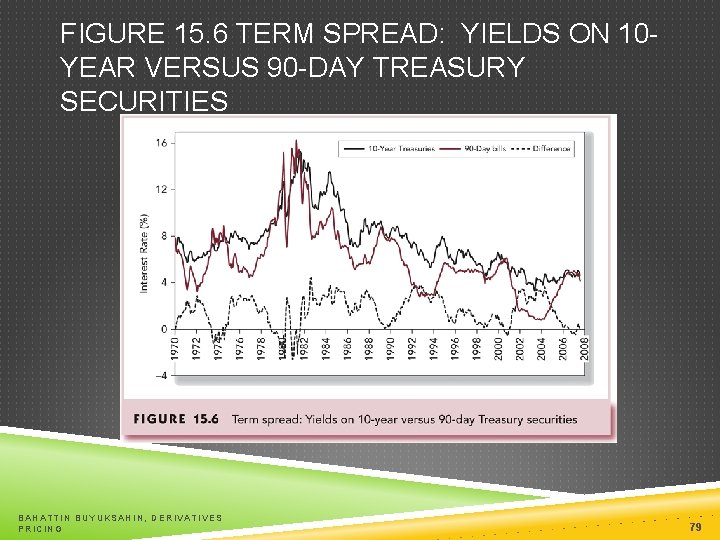
FIGURE 15. 6 TERM SPREAD: YIELDS ON 10 YEAR VERSUS 90 -DAY TREASURY SECURITIES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 79

FORWARD RATES AS FORWARD CONTRACTS In general, forward rates will not equal the eventually realized short rate Still an important consideration when trying to make decisions : Locking in loan rates BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 80

FIGURE 15. 7 ENGINEERING A SYNTHETIC FORWARD LOAN BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 81

CHAPTER 16 Managing Bond Portfolios BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 82

BOND PRICING RELATIONSHIPS Inverse relationship between price and yield An increase in a bond’s yield to maturity results in a smaller price decline than the gain associated with a decrease in yield Long-term bonds tend to be more price sensitive than short-term bonds BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 83
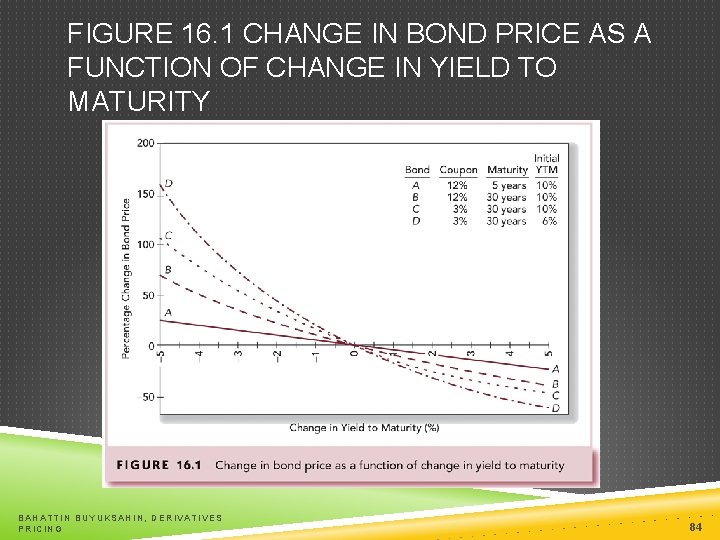
FIGURE 16. 1 CHANGE IN BOND PRICE AS A FUNCTION OF CHANGE IN YIELD TO MATURITY BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 84

BOND PRICING RELATIONSHIPS CONTINUED As maturity increases, price sensitivity increases at a decreasing rate Price sensitivity is inversely related to a bond’s coupon rate Price sensitivity is inversely related to the yield to maturity at which the bond is selling BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 85

TABLE 16. 1 PRICES OF 8% COUPON BOND (COUPONS PAID SEMIANNUALLY) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 86
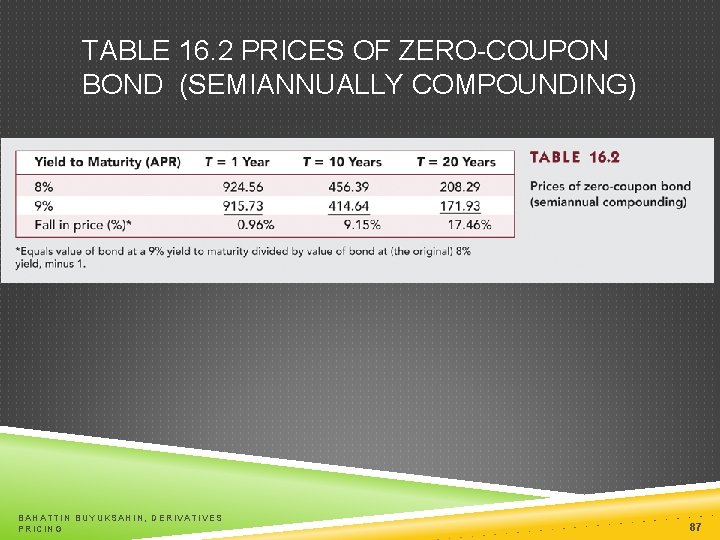
TABLE 16. 2 PRICES OF ZERO-COUPON BOND (SEMIANNUALLY COMPOUNDING) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 87

DURATION A measure of the effective maturity of a bond The weighted average of the times until each payment is received, with the weights proportional to the present value of the payment Duration is shorter than maturity for all bonds except zero coupon bonds Duration is equal to maturity for zero coupon bonds BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 88

DURATION: CALCULATION BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 89
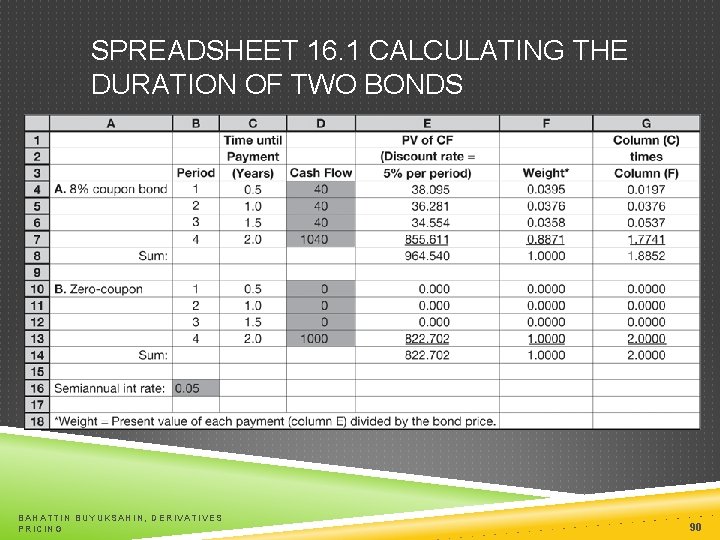
SPREADSHEET 16. 1 CALCULATING THE DURATION OF TWO BONDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 90
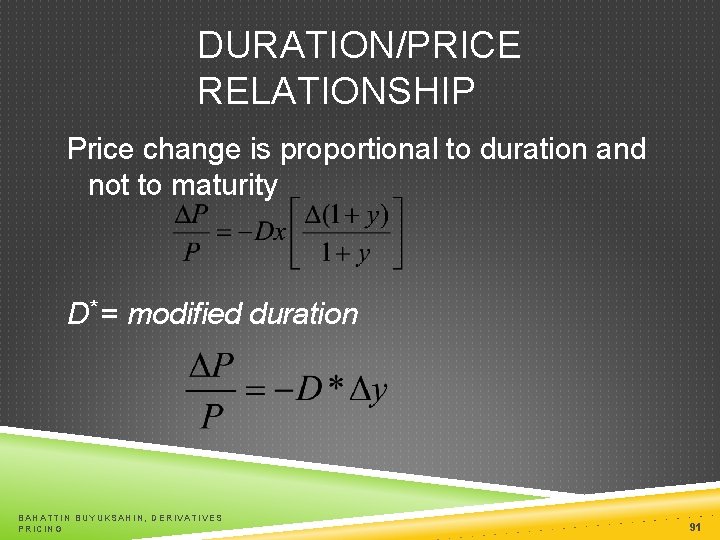
DURATION/PRICE RELATIONSHIP Price change is proportional to duration and not to maturity D* = modified duration BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 91

RULES FOR DURATION Rule 1 The duration of a zero-coupon bond equals its time to maturity Rule 2 Holding maturity constant, a bond’s duration is higher when the coupon rate is lower Rule 3 Holding the coupon rate constant, a bond’s duration generally increases with its time to maturity Rule 4 Holding other factors constant, the duration of a coupon bond is higher when the bond’s yield to maturity is lower Rules 5 The duration of a level perpetuity is equal to: (1+y) / y BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 92
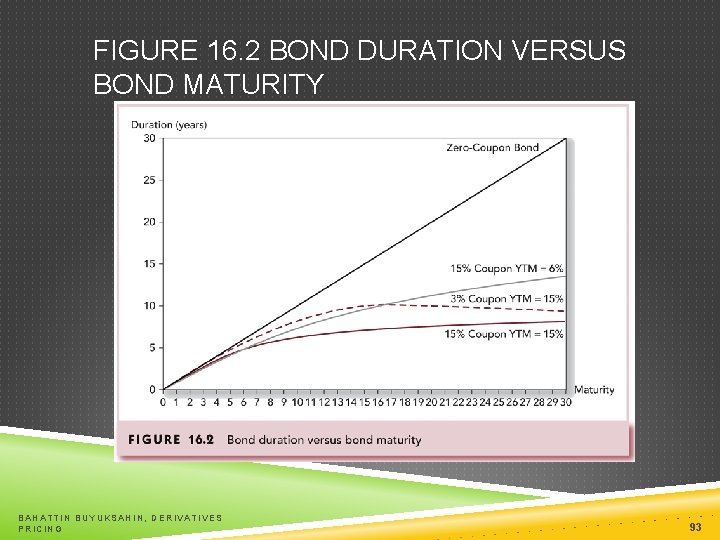
FIGURE 16. 2 BOND DURATION VERSUS BOND MATURITY BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 93
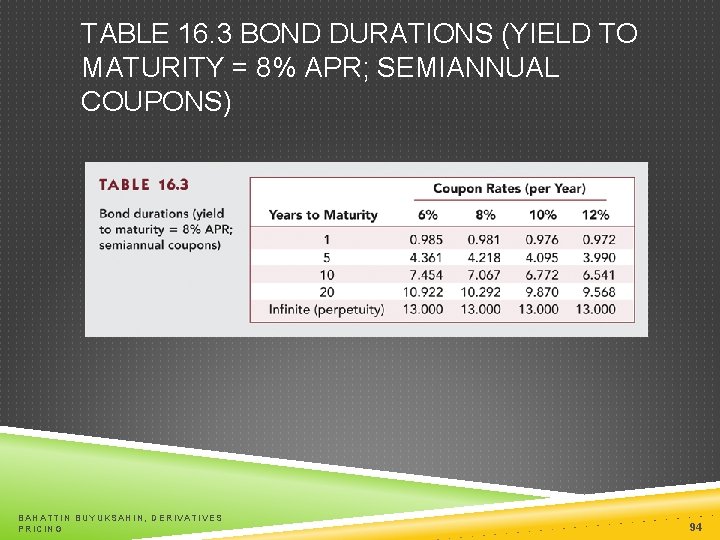
TABLE 16. 3 BOND DURATIONS (YIELD TO MATURITY = 8% APR; SEMIANNUAL COUPONS) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 94

CONVEXITY The relationship between bond prices and yields is not linear Duration rule is a good approximation for only small changes in bond yields BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 95
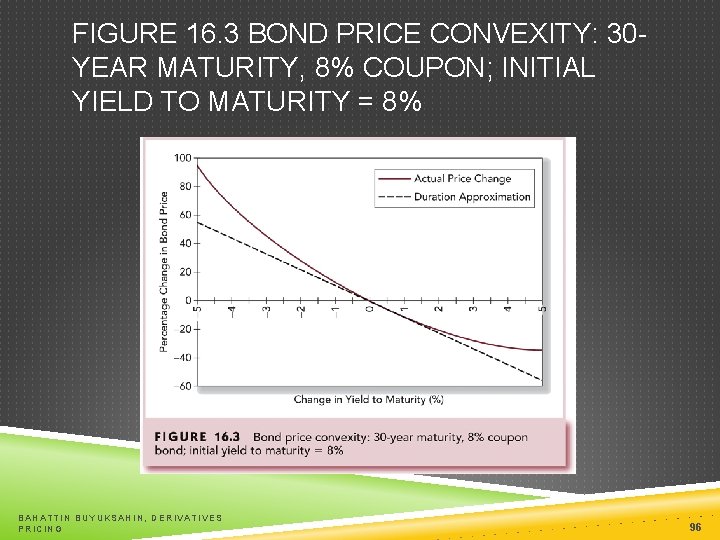
FIGURE 16. 3 BOND PRICE CONVEXITY: 30 YEAR MATURITY, 8% COUPON; INITIAL YIELD TO MATURITY = 8% BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 96

CORRECTION FOR CONVEXITY Correction for Convexity: BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 97
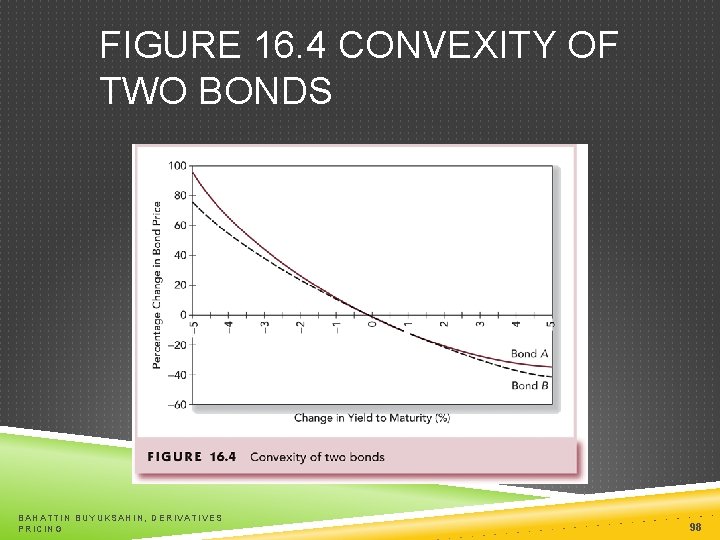
FIGURE 16. 4 CONVEXITY OF TWO BONDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 98

CALLABLE BONDS As rates fall, there is a ceiling on possible prices The bond cannot be worth more than its call price Negative convexity Use effective duration: BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 99
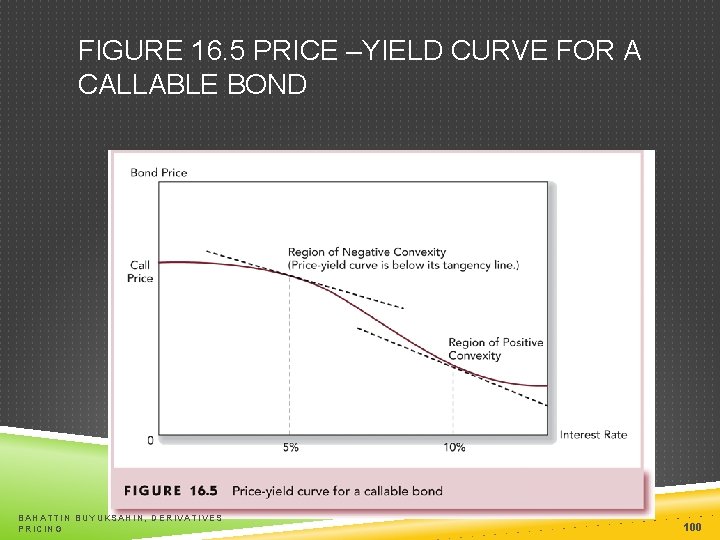
FIGURE 16. 5 PRICE –YIELD CURVE FOR A CALLABLE BOND BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 100

MORTGAGE-BACKED SECURITIES Among the most successful examples of financial engineering Subject to negative convexity Often sell for more than their principal balance Homeowners do not refinance their loans as soon as interest rates drop BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 101
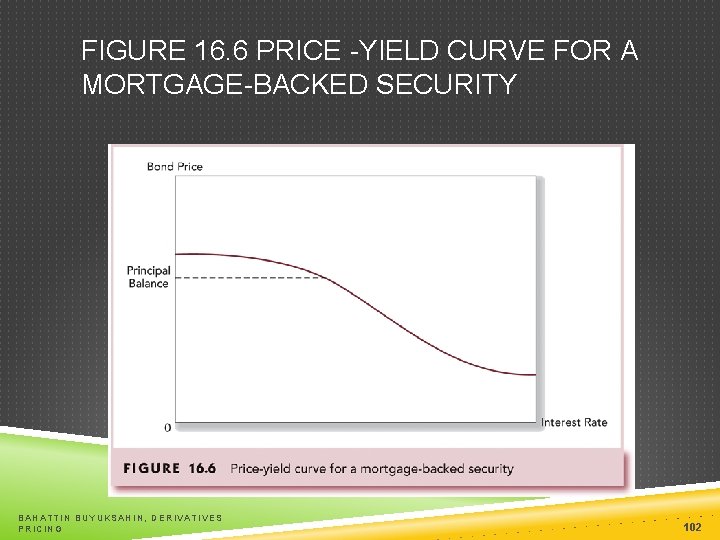
FIGURE 16. 6 PRICE -YIELD CURVE FOR A MORTGAGE-BACKED SECURITY BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 102

MORTGAGE-BACKED SECURITIES CONTINUED They have given rise to many derivatives including the CMO (collateralized mortgage obligation) Use of tranches BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 103
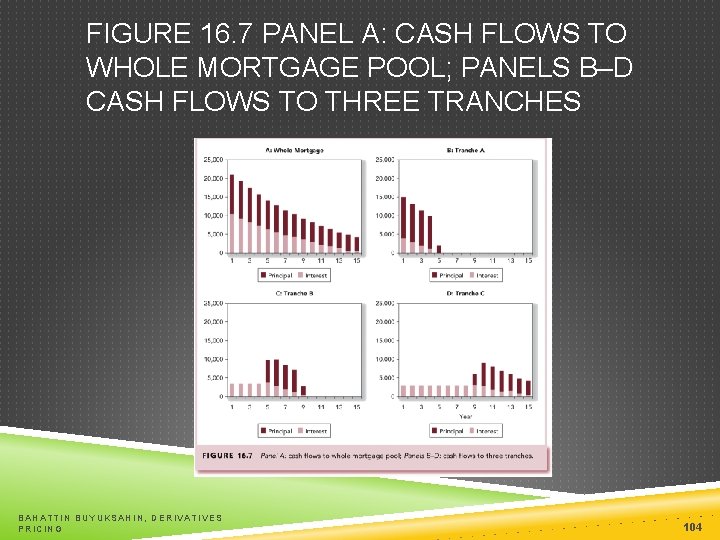
FIGURE 16. 7 PANEL A: CASH FLOWS TO WHOLE MORTGAGE POOL; PANELS B–D CASH FLOWS TO THREE TRANCHES BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 104

PASSIVE MANAGEMENT Bond-Index Funds Immunization of interest rate risk: Net worth immunization Duration of assets = Duration of liabilities Target date immunization Holding Period matches Duration BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 105
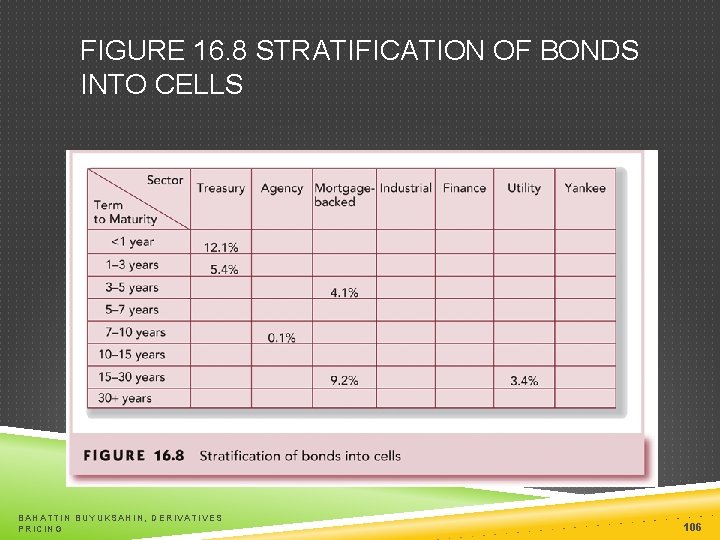
FIGURE 16. 8 STRATIFICATION OF BONDS INTO CELLS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 106
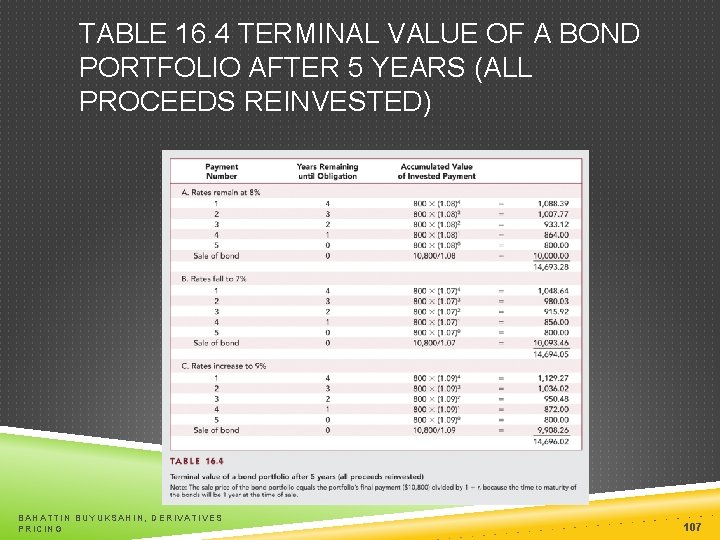
TABLE 16. 4 TERMINAL VALUE OF A BOND PORTFOLIO AFTER 5 YEARS (ALL PROCEEDS REINVESTED) BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 107
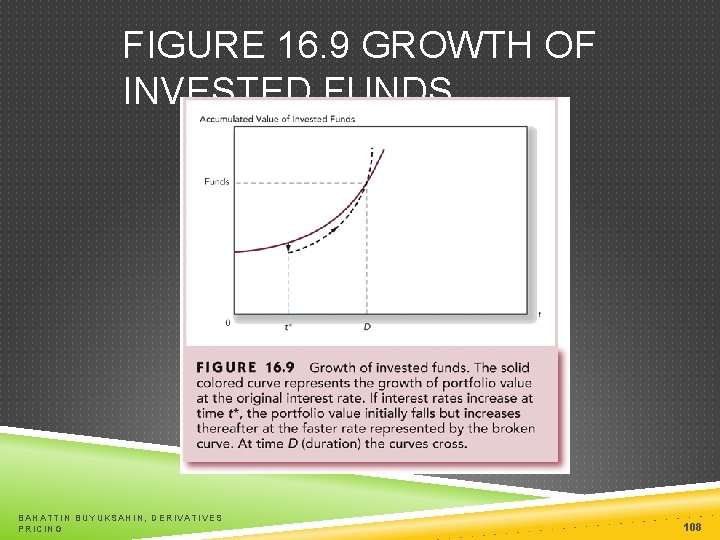
FIGURE 16. 9 GROWTH OF INVESTED FUNDS BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 108
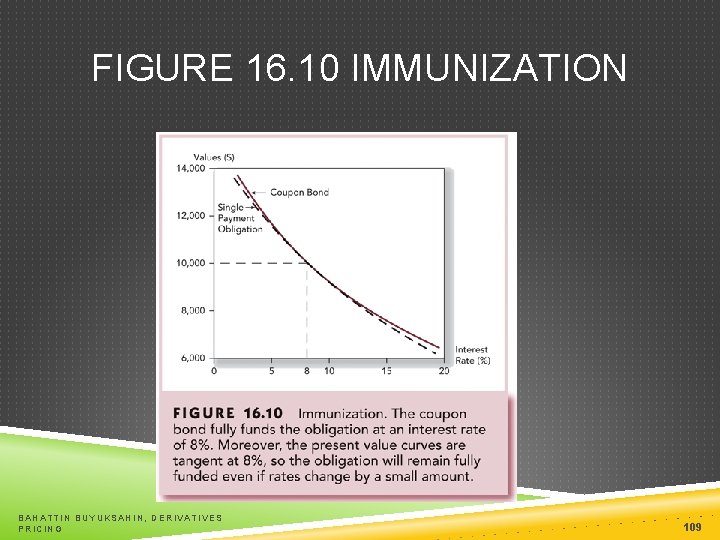
FIGURE 16. 10 IMMUNIZATION BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 109
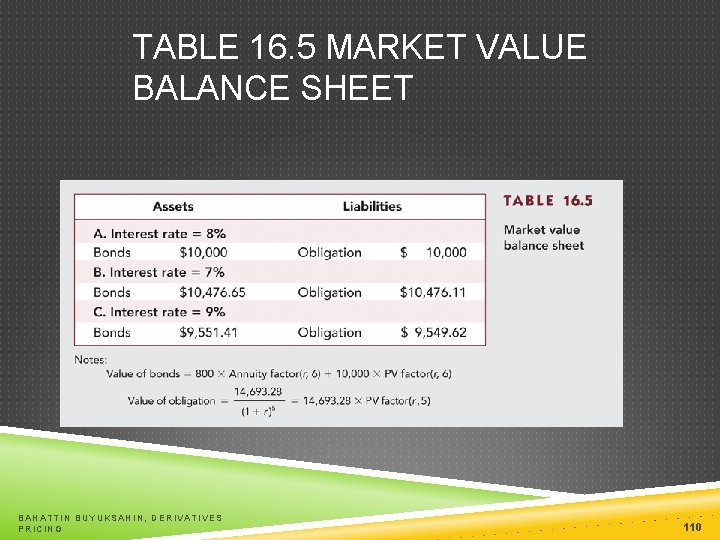
TABLE 16. 5 MARKET VALUE BALANCE SHEET BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 110

CASH FLOW MATCHING AND DEDICATION Automatically immunize the portfolio from interest rate movement Cash flow and obligation exactly offset each other i. e. Zero-coupon bond Not widely used because of constraints associated with bond choices Sometimes it simply is not possible to do BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 111

ACTIVE MANAGEMENT: SWAPPING STRATEGIES Substitution swap Intermarket swap Rate anticipation swap Pure yield pickup Tax swap BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 112

HORIZON ANALYSIS Select a particular holding period and predict the yield curve at end of period Given a bond’s time to maturity at the end of the holding period Its yield can be read from the predicted yield curve and the end-of-period price can be calculated BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 113

CONTINGENT IMMUNIZATION A combination of active and passive management The strategy involves active management with a floor rate of return As long as the rate earned exceeds the floor, the portfolio is actively managed Once the floor rate or trigger rate is reached, the portfolio is immunized BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 114
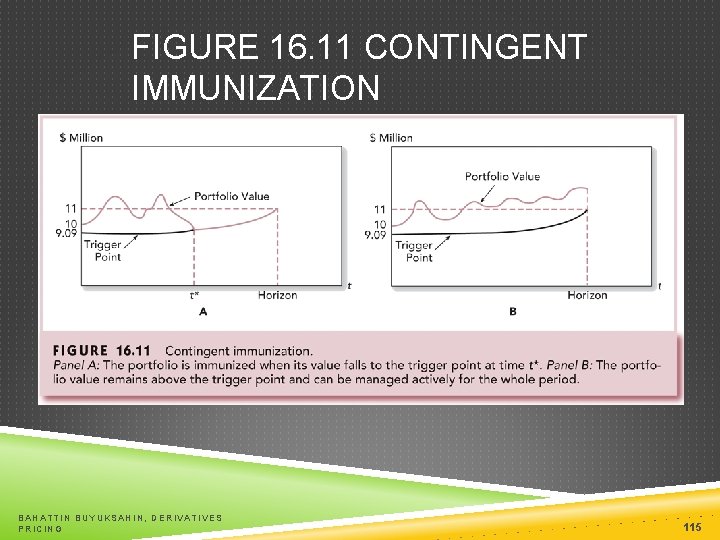
FIGURE 16. 11 CONTINGENT IMMUNIZATION BAHATTIN BUYUKSAHIN, DERIVATIVES PRICING 115
- Slides: 115