Bohrs Model atomic energy levels Electrons could only
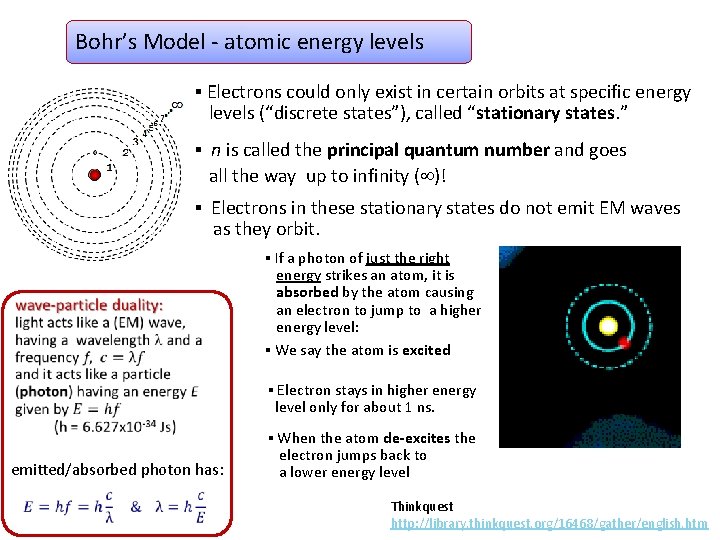
Bohr’s Model - atomic energy levels ▪ Electrons could only exist in certain orbits at specific energy levels (“discrete states”), called “stationary states. ” ▪ n is called the principal quantum number and goes all the way up to infinity ( )! ▪ Electrons in these stationary states do not emit EM waves as they orbit. ▪ If a photon of just the right energy strikes an atom, it is absorbed by the atom causing an electron to jump to a higher energy level: ▪ We say the atom is excited ▪ Electron stays in higher energy level only for about 1 ns. emitted/absorbed photon has: ▪ When the atom de-excites the electron jumps back to a lower energy level Thinkquest http: //library. thinkquest. org/16468/gather/english. htm
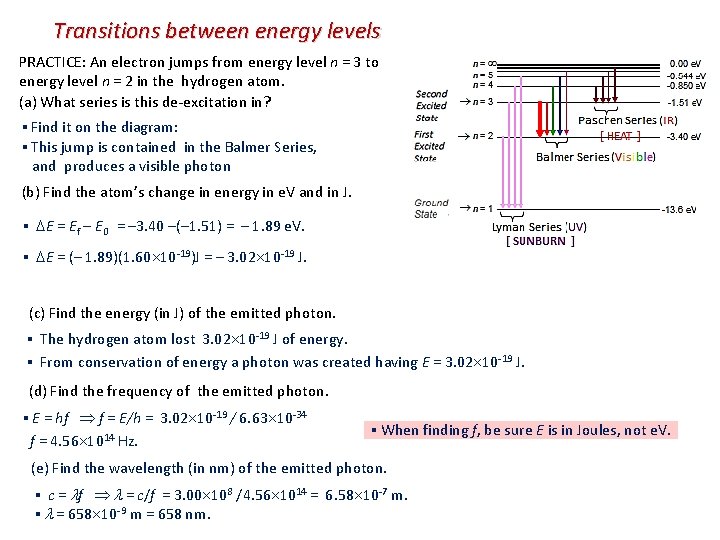
Transitions between energy levels PRACTICE: An electron jumps from energy level n = 3 to energy level n = 2 in the hydrogen atom. (a) What series is this de-excitation in? ▪ Find it on the diagram: ▪ This jump is contained in the Balmer Series, and produces a visible photon (b) Find the atom’s change in energy in e. V and in J. ▪ E = Ef – E 0 = – 3. 40 –(– 1. 51) = – 1. 89 e. V. ▪ E = (– 1. 89)(1. 60 10 -19)J = – 3. 02 10 -19 J. (c) Find the energy (in J) of the emitted photon. ▪ The hydrogen atom lost 3. 02 10 -19 J of energy. ▪ From conservation of energy a photon was created having E = 3. 02 10 -19 J. (d) Find the frequency of the emitted photon. ▪ E = hf f = E/h = 3. 02 10 -19 / 6. 63 10 -34 f = 4. 56 1014 Hz. ▪ When finding f, be sure E is in Joules, not e. V. (e) Find the wavelength (in nm) of the emitted photon. ▪ c = f = c/f = 3. 00 108 /4. 56 1014 = 6. 58 10 -7 m. ▪ = 658 10 -9 m = 658 nm.

Discrete energy and discrete energy levels ▪ Discrete means discontinuous, or separated PRACTICE: Which one of the following provides direct evidence for the existence of discrete energy levels in an atom? A. The continuous spectrum of the light emitted by a white hot metal. B. The line emission spectrum of a gas at low pressure. C. The emission of gamma radiation from radioactive atoms. D. The ionization of gas atoms when bombarded by alpha particles.
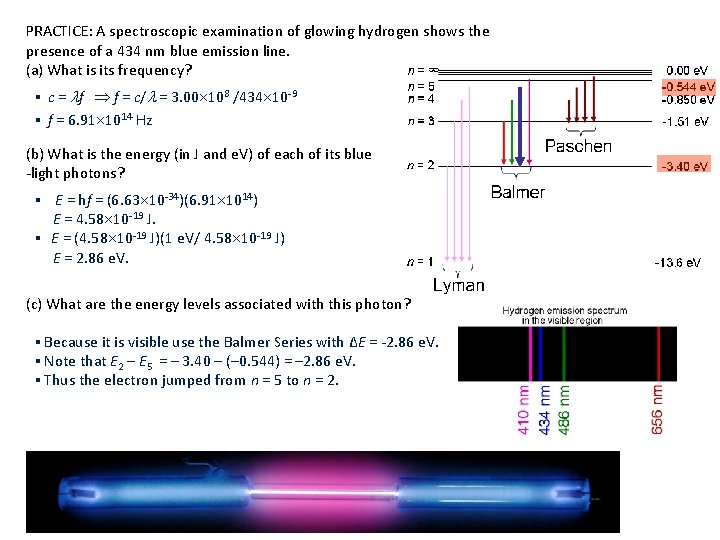
PRACTICE: A spectroscopic examination of glowing hydrogen shows the presence of a 434 nm blue emission line. (a) What is its frequency? ▪ c = f f = c/ = 3. 00 108 /434 10 -9 ▪ f = 6. 91 1014 Hz (b) What is the energy (in J and e. V) of each of its blue -light photons? ▪ E = hf = (6. 63 10 -34)(6. 91 1014) E = 4. 58 10 -19 J. ▪ E = (4. 58 10 -19 J)(1 e. V/ 4. 58 10 -19 J) E = 2. 86 e. V. (c) What are the energy levels associated with this photon? ▪ Because it is visible use the Balmer Series with ∆E = -2. 86 e. V. ▪ Note that E 2 – E 5 = – 3. 40 – (– 0. 544) = – 2. 86 e. V. ▪ Thus the electron jumped from n = 5 to n = 2.
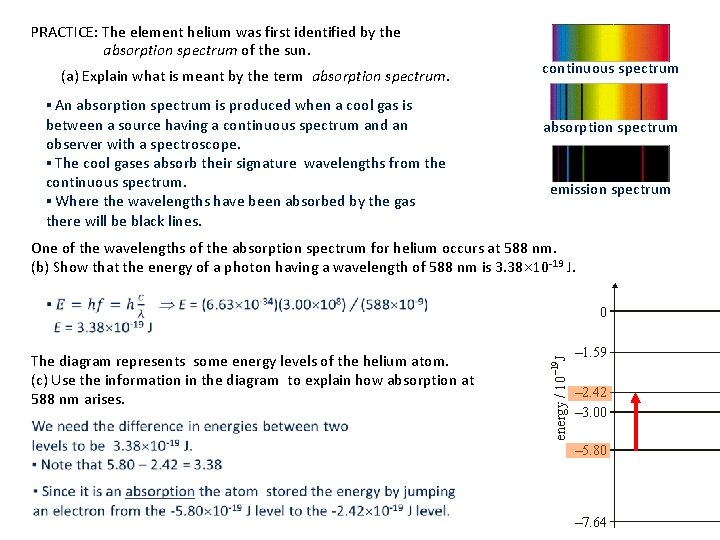
PRACTICE: The element helium was first identified by the absorption spectrum of the sun. (a) Explain what is meant by the term absorption spectrum. ▪ An absorption spectrum is produced when a cool gas is between a source having a continuous spectrum and an observer with a spectroscope. ▪ The cool gases absorb their signature wavelengths from the continuous spectrum. ▪ Where the wavelengths have been absorbed by the gas there will be black lines. continuous spectrum absorption spectrum emission spectrum One of the wavelengths of the absorption spectrum for helium occurs at 588 nm. (b) Show that the energy of a photon having a wavelength of 588 nm is 3. 38 10 -19 J. The diagram represents some energy levels of the helium atom. (c) Use the information in the diagram to explain how absorption at 588 nm arises.

Isotopes PRACTICE: Which of the following gives the correct number of electrons, protons and neutrons in the neutral atom 65 Cu? 29 A = 65, Z = 29, so N = A – Z = 65 – 29 = 36. Since it is neutral, the number of electrons equals the number of protons = Z = 29.

Isotopes PRACTICE: Ag-102, Ag-103 and Ag-104 are all isotopes of the element silver. Which one of the following is a true statement about the nuclei of these isotopes? A. All have the same mass. B. All have the same number of nucleons. C. All have the same number of neutrons. D. All have the same number of protons. Isotopes of an element have different masses and nucleon totals. Isotopes of an element have the same number of protons, and by extension, electrons. This is why their chemical properties are identical.
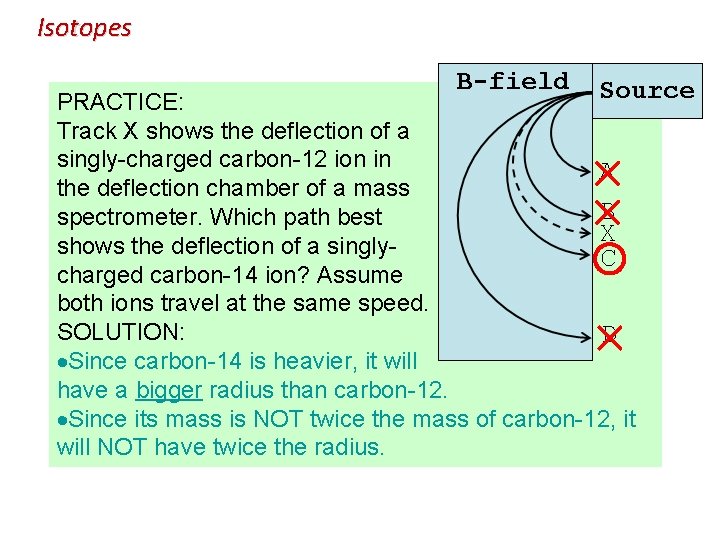
Isotopes PRACTICE: Track X shows the deflection of a singly-charged carbon-12 ion in the deflection chamber of a mass spectrometer. Which path best shows the deflection of a singlycharged carbon-14 ion? Assume both ions travel at the same speed. SOLUTION: Since carbon-14 is heavier, it will have a bigger radius than carbon-12. Since its mass is NOT twice the mass of carbon-12, it will NOT have twice the radius.

Fundamental forces and their properties PRACTICE: The nucleus of an atom contains protons. The protons are prevented from flying apart by A. The presence of orbiting electrons. B. The presence of gravitational forces. C. The presence of strong attractive nuclear forces. D. The absence of Coulomb repulsive forces at nuclear distances. It is the presence of the strong force within the nucleus. PRACTICE: Use Coulomb’s law to find the repulsive force between two protons in a helium nucleus. Assume the nucleus is 1. 00 10 -15 m in diameter and that the protons are as far apart as they can get. F = ke 2 / r 2 = 9 109(1. 6 10 -19)2 / (1. 00 10 -15)2 F = 230 N. From chemistry we know that atoms can be separated from each other and moved easily. This tells us that at the range of about 10 -10 m (the atomic diameter), the strong force is zero.
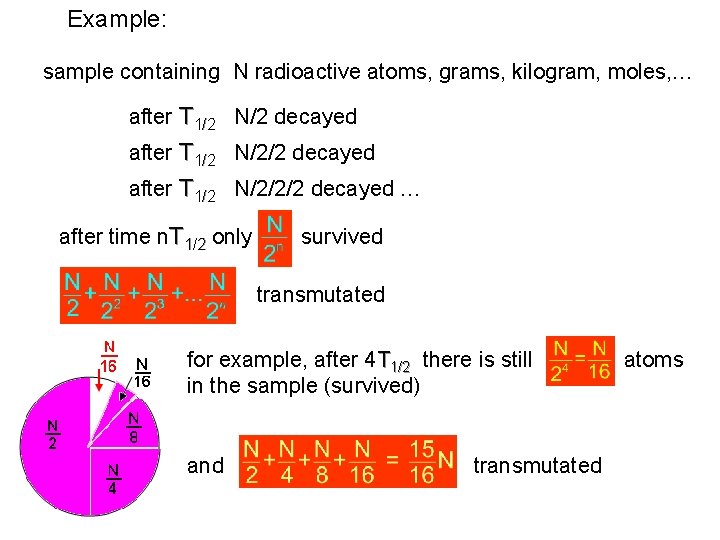
Example: sample containing N radioactive atoms, grams, kilogram, moles, … after T 1/2 N/2 decayed after T 1/2 N/2/2/2 decayed … after time n. T 1/2 only survived transmutated for example, after 4 T 1/2 there is still in the sample (survived) and transmutated atoms

Example: Cobalt– 60 decays by beta emission and has a half-life of aproximately 5 years. If a sample of cobalt– 60 emits 40 beta particles per second, how many will the sample be emitting in 15 years time? After 5 years activity will be 20/sec (number of decays/sec). After another 5 years it will be 10/sec. Finally after a further 5 years it will emit 5 particles/sec.
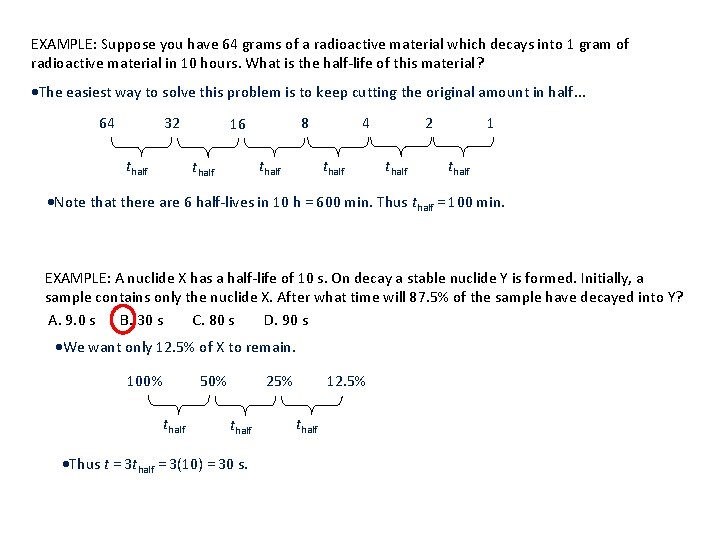
EXAMPLE: Suppose you have 64 grams of a radioactive material which decays into 1 gram of radioactive material in 10 hours. What is the half-life of this material? The easiest way to solve this problem is to keep cutting the original amount in half. . . 32 64 thalf 1 2 4 8 16 thalf Note that there are 6 half-lives in 10 h = 600 min. Thus thalf = 100 min. EXAMPLE: A nuclide X has a half-life of 10 s. On decay a stable nuclide Y is formed. Initially, a sample contains only the nuclide X. After what time will 87. 5% of the sample have decayed into Y? A. 9. 0 s B. 30 s C. 80 s D. 90 s We want only 12. 5% of X to remain. thalf 12. 5% 25% 50% 100% thalf Thus t = 3 thalf = 3(10) = 30 s. thalf
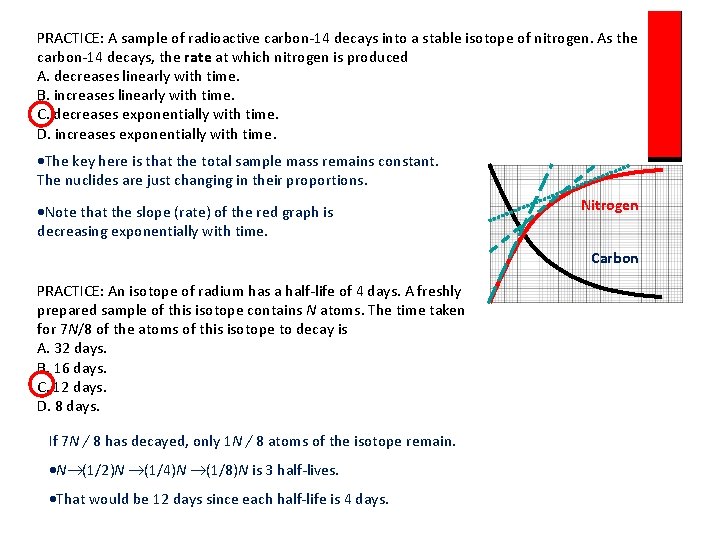
PRACTICE: A sample of radioactive carbon-14 decays into a stable isotope of nitrogen. As the carbon-14 decays, the rate at which nitrogen is produced A. decreases linearly with time. B. increases linearly with time. C. decreases exponentially with time. D. increases exponentially with time. The key here is that the total sample mass remains constant. The nuclides are just changing in their proportions. Note that the slope (rate) of the red graph is decreasing exponentially with time. Nitrogen Carbon PRACTICE: An isotope of radium has a half-life of 4 days. A freshly prepared sample of this isotope contains N atoms. The time taken for 7 N/8 of the atoms of this isotope to decay is A. 32 days. B. 16 days. C. 12 days. D. 8 days. If 7 N / 8 has decayed, only 1 N / 8 atoms of the isotope remain. N (1/2)N (1/4)N (1/8)N is 3 half-lives. That would be 12 days since each half-life is 4 days.

PRACTICE: Radioactive decay is a random process. This means that A. a radioactive sample will decay continuously. B. some nuclei will decay faster than others. C. it cannot be predicted how much energy will be released. D. it cannot be predicted when a particular nucleus will decay. Random process PRACTICE: Isotopes of an element have the same number of protons and electrons, but different numbers of neutrons
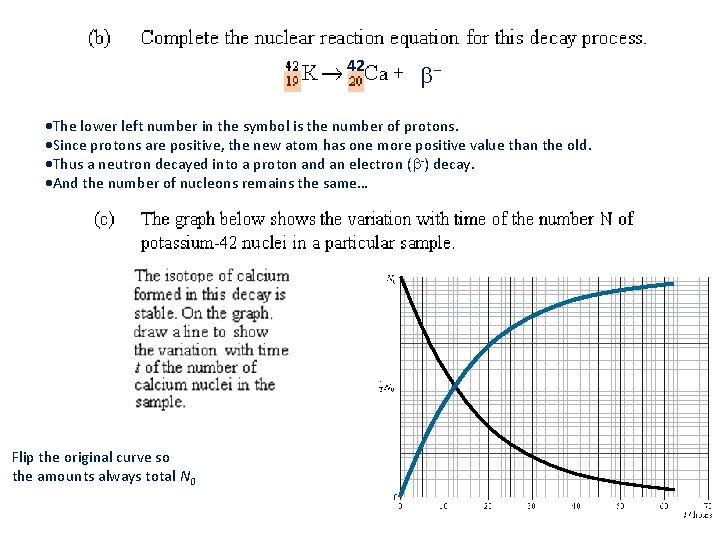
42 - The lower left number in the symbol is the number of protons. Since protons are positive, the new atom has one more positive value than the old. Thus a neutron decayed into a proton and an electron ( -) decay. And the number of nucleons remains the same… Flip the original curve so the amounts always total N 0

It is the gamma decay that leads us to the conclusion that excited nuclei, just like excited atoms, release photons of discrete energy, implying discrete energy levels. Since the ratio is 1/2, for each nickel atom there are 2 cobalt atoms. Thus, out of every three atoms, 1 is nickel and 2 are cobalt. Therefore, the remaining cobalt is (2/3)N 0. -ray decay happens when the nucleus goes from an excited state to a de-excited state.
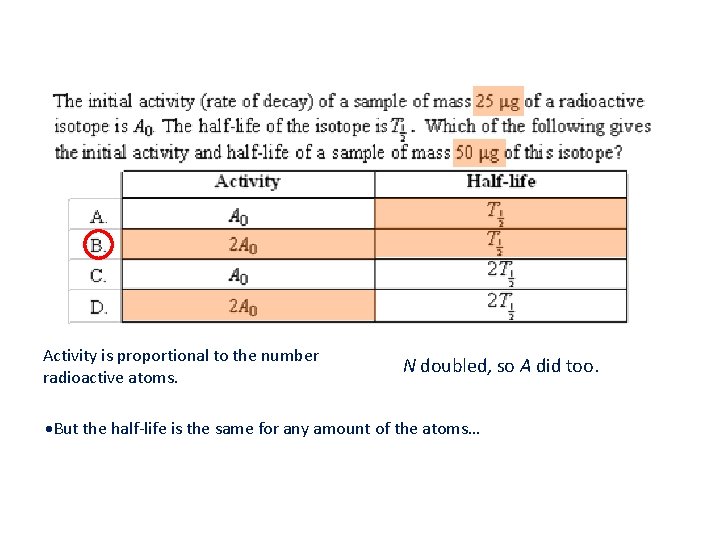
Activity is proportional to the number radioactive atoms. N doubled, so A did too. But the half-life is the same for any amount of the atoms…

Activity is proportional to the number radioactive atoms remaining in the sample. Since X’s half-life is shorter than Y’s, less activity will be due to X, and more to Y at any later date… 60 days is 2 half-lives for P so NP is 1/4 of what it started out as. 60 days is 3 half-lives for Q so NQ is 1/8 of what it started out as. Thus NP / NQ = (1/4) / (1/8) = (1/4) (8/1) = 8/4 = 2.

Nuclear reactions Just know this!

Nuclear reactions There are many ways to attack this problem. First of all, alpha particles are 4 He, not 2 He. (Also, P has an atomic number of 15, not 14). Secondly, a proton has a Z number of 1, not zero.
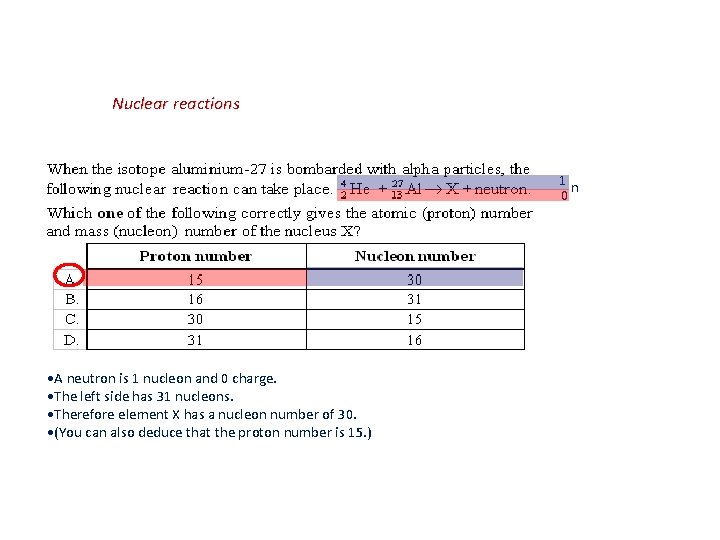
Nuclear reactions 1 n 0 A neutron is 1 nucleon and 0 charge. The left side has 31 nucleons. Therefore element X has a nucleon number of 30. (You can also deduce that the proton number is 15. )

Nuclear reactions 0 + -1 e + The nucleon number is already balanced. The charge on the right is high. These two numbers are characteristic of the electron. The process is beta-minus decay. Don’t forget the antineutrino that goes with beta-minus.

Nuclear reactions Keep in mind that an electron has N = 0 and Z = -1. Thus only one of the above choices is possible. .

The unified atomic mass unit (amu abbreviated as u) In the world of nuclear reactions we have to keep very precise track of the mass of the nuclei if we ▪ are to determine the energy of a reaction. 1 u = 1/12 of the mass of one atom of carbon-12 (6 p+6 n+6 e) ▪ 1 u = 1. 66053886 x 10 -27 kg

The unified atomic mass unit expressed in different units ▪ 1 u = 1. 66053886 x 10 -27 kg 1 Me. V = 106 e. V = 1. 6 x 10 -13 J 1 u can be converted into 1. 492 x 10 -10 J = 931. 5 Me. V energy: Using E = mc 2 m=E/c 2 we can convert the units for mass (kg) into alternative units. 1 u = 1. 661 10 -27 kg = 931. 5 Me. V c-2

Mass defect and nuclear binding energy EXAMPLE: (a) Label the reactants and the products in the following nuclear reaction: 2( 1 H) + 2 n 4 He. reactants product (b) Using the table find the mass defect in that nuclear reaction: ▪ nucleons: 2(1. 007825) + 2(1. 008665) = 4. 032980 u. m 1 + m 2 ▪ nucleus: 4. 002603 u. >M 10 -29 kg. ▪ The mass defect: ∆m = 4. 002603 - 4. 032890 = -0. 030377 u = -5. 044 (c) What is the binding energy Eb in 4 He in the nuclear reaction 2(1 H) + 2 n 4 He? Particle Masses Particle Mass (u) Electron 0. 000548 Proton 1. 00727 1 H atom 1. 007825 Neutron 1. 008665 4 He atom 4. 002603 mass deficit is converted into energy BE = ∆m c 2 released in assembling a nucleus from its individual nucleons. BE = ∆m c 2 = (5. 044 10 -29)(3. 00 108)2 = 4. 54 10 -12 J. or: 1 u can be converted 931. 5 Me. V energy, so ▪ Thus 4 He has less mass than its constituents! Thus, to pull apart the 4 He and separate it into its constituents, BE=28. 30 Me. V is needed to create that extra mass.

Mass defect in nuclear decay: A → C + D is positive ▪ M > m 1 + m 2 ▪ What happened to that mass difference? ▪ Energy corresponding to that mass difference is released as kinetic energy of the products Mass of aluminum-29 nucleus = 28. 97330 u Mass of silicon-29 nucleus + b-particle + antineutrino = 28. 96880 u + 0. 000549 u + 0 = 28. 969349 u ▪ Mass difference = 28. 97330 u – 28. 969349 u = 0. 003951 u BE= 3. 68 Me. V ▪ Again this becomes the kinetic energy of the decay products.

Mass defect in nuclear decay: A → C + D is positive PRACTICE: Radium-226 (226 Ra) undergoes natural radioactive decay to disintegrate spontaneously with the emission of an alpha particle to form radon (Rn). Calculate the energy in Joules and Me. V that is released M > m 1 + m 2 total energy on the left = total energy on the right
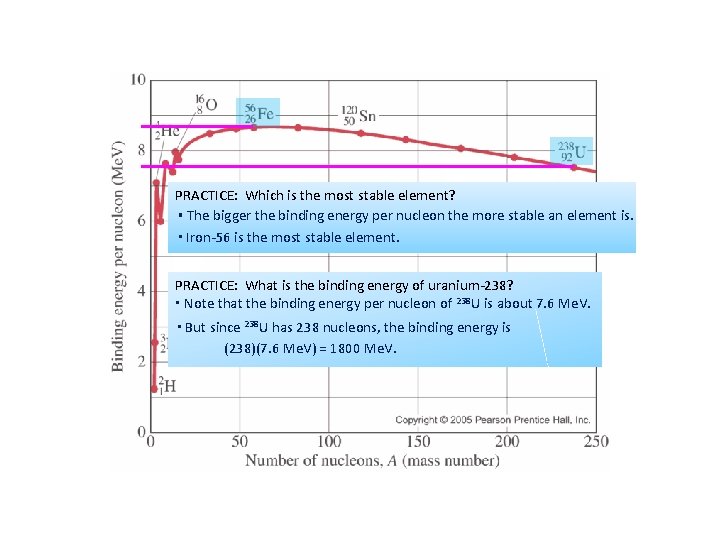
PRACTICE: Which is the most stable element? ▪ The bigger the binding energy per nucleon the more stable an element is. ▪ Iron-56 is the most stable element. PRACTICE: What is the binding energy of uranium-238? ▪ Note that the binding energy per nucleon of 238 U is about 7. 6 Me. V. ▪ But since 238 U has 238 nucleons, the binding energy is (238)(7. 6 Me. V) = 1800 Me. V.
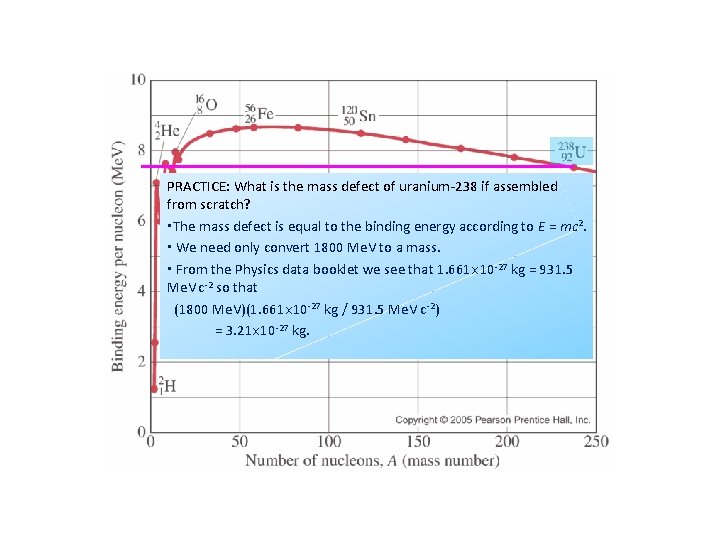
PRACTICE: What is the mass defect of uranium-238 if assembled from scratch? ▪The mass defect is equal to the binding energy according to E = mc 2. ▪ We need only convert 1800 Me. V to a mass. ▪ From the Physics data booklet we see that 1. 661 10 -27 kg = 931. 5 Me. V c-2 so that (1800 Me. V)(1. 661 10 -27 kg / 931. 5 Me. V c-2) = 3. 21 10 -27 kg.

Sketching and interpreting the graph of average binding energy per nucleon against nucleon number PRACTICE: 54 Fe has a mass of 53. 9396 u. A proton (with electron) has a mass of 1. 00782 u and a neutron has a mass of 1. 00866 u. (a) Find the binding energy of iron-54 in Me. V. SOLUTION: 54 Fe: A = 54, Z = 26, N = 54 - 26 = 28. ▪ The constituents of 54 Fe are thus: 26(1. 00782 u) + 28(1. 00866 u) = 54. 4458 u ▪ The mass defect is thus ∆m = 54. 4458 u – 53. 9396 u = 0. 5062 u ▪ The binding energy is thus BE = (0. 5062)(931. 5 Me. V) = 471. 5 Me. V. (b) Find the binding energy per nucleon of iron-54. SOLUTION: 54 Fe: A = 54, Z = 26, N = 54 – 26 = 28. ▪ The binding energy is BE = 471. 5 Me. V. ▪ The number of nucleons is A = 54. ▪ Thus the binding energy per nucleon is BE / A = 471. 5 Me. V / 54 nucleons = 8. 7 Me. V / nucleon. ▪ This is consistent with the graph.
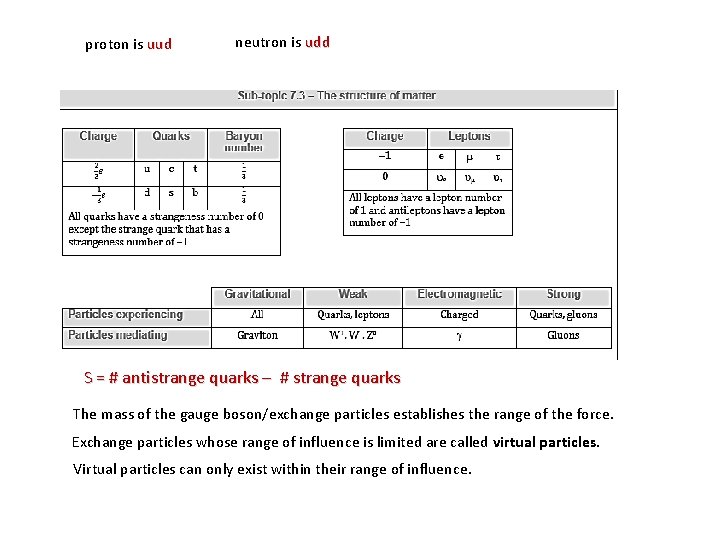
proton is uud neutron is udd S = # antistrange quarks – # strange quarks The mass of the gauge boson/exchange particles establishes the range of the force. Exchange particles whose range of influence is limited are called virtual particles. Virtual particles can only exist within their range of influence.
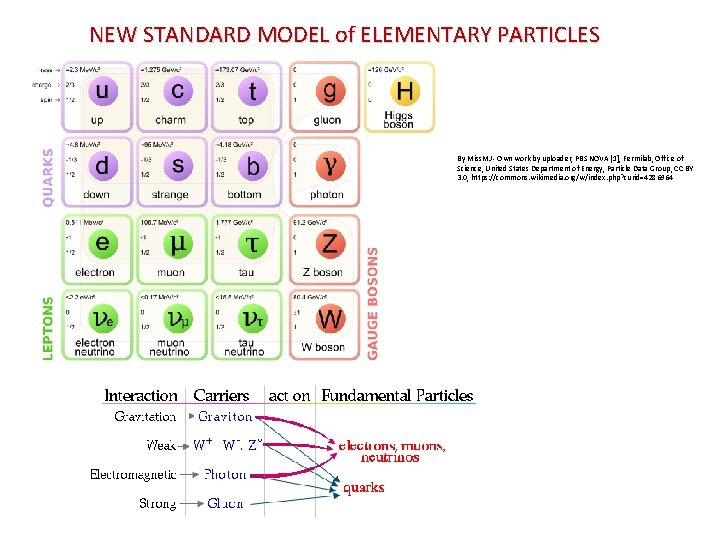
NEW STANDARD MODEL of ELEMENTARY PARTICLES By Miss. MJ - Own work by uploader, PBS NOVA [1], Fermilab, Office of Science, United States Department of Energy, Particle Data Group, CC BY 3. 0, https: //commons. wikimedia. org/w/index. php? curid=4286964

conservation rules in reactions ▪ charge is conserved ▪ baryon number is conserved ▪ lepton number is conserved ▪ strangeness is conserved ▪ Quark confinement means that we cannot ever separate a single quark from a baryon or a meson. ▪ Because of the nature of the strong force holding the quarks together we need to provide an energy that is proportional to the separation. ▪ Eventually, that energy is so vast that a new quark-antiquark pair forms and all we have is a meson, instead of an isolated quark!

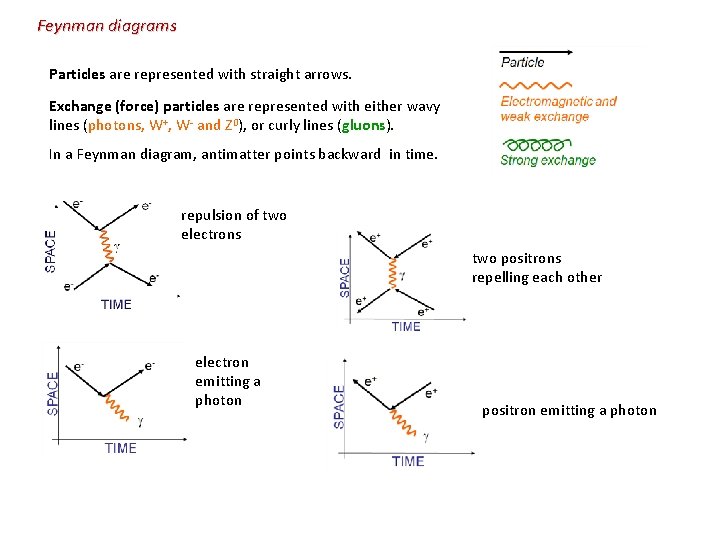
Feynman diagrams Particles are represented with straight arrows. Exchange (force) particles are represented with either wavy lines (photons, W+, W- and Z 0), or curly lines (gluons). In a Feynman diagram, antimatter points backward in time. repulsion of two electrons two positrons repelling each other electron emitting a photon positron emitting a photon
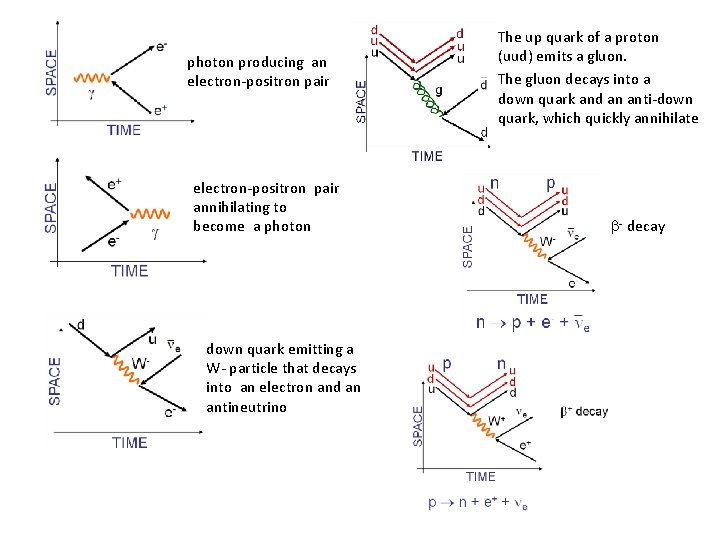
photon producing an electron-positron pair annihilating to become a photon down quark emitting a W- particle that decays into an electron and an antineutrino The up quark of a proton (uud) emits a gluon. The gluon decays into a down quark and an anti-down quark, which quickly annihilate - decay
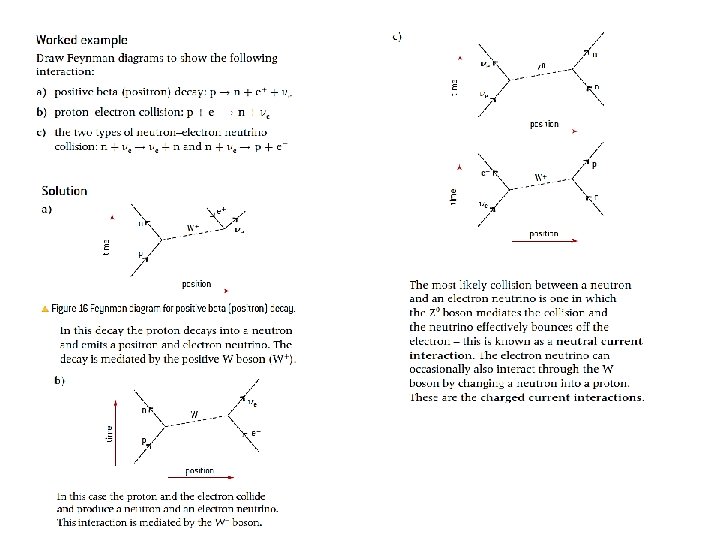
- Slides: 38