Bohr Model of Particle Motion In the Schwarzschild

Bohr Model of Particle Motion In the Schwarzschild Metric Weldon J. Wilson Department of Physics University of Central Oklahoma Edmond, Oklahoma Email: wwilson@ucok. edu WWW: http: //www. physics. ucok. edu/~wwilson

OUTLINE n n n Schwarzschild Metric Effective Potential Bound States - Circular Orbits Bohr Quantization Summary

SCHWARZSCHILD METRIC where Leads to the action And corresponding Lagrangian

HAMILTONIAN FORMULATION Using the standard procedure, the Lagrangian With Yields the Hamiltonian

ORBITAL MOTION The Hamiltonian Leads to planar orbits with conserved angular momentum Using

CIRCULAR ORBITS For circular orbits And the Hamiltonian becomes 0

EFFECTIVE POTENTIAL The Hamiltonian for circular orbits is the total energy (rest energy + effective potential energy) of the mass m in a circular orbit of radius R in the “field” of the mass M.
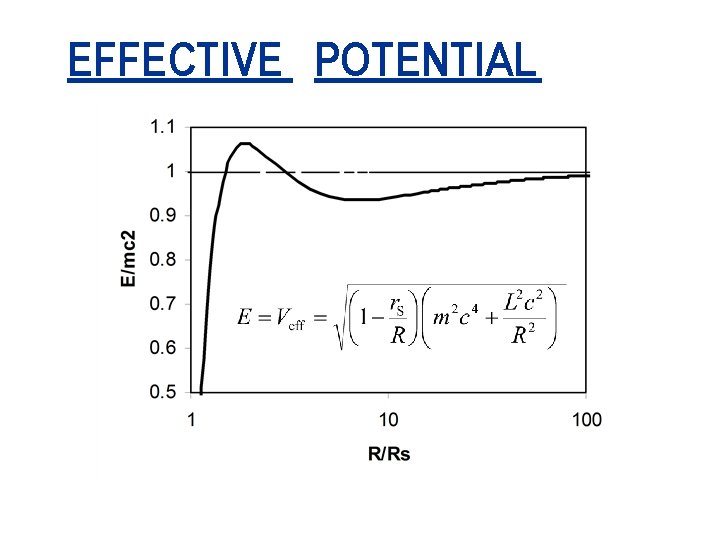
EFFECTIVE POTENTIAL

RADIAL FORCE EQUATION The radial force equation can be obtained from Differentiation gives Which must vanish for the circular orbit ( )

ALLOWED RADII OF ORBITS Setting For the circular orbits produces the quadratic Which can be solved for the allowed radii
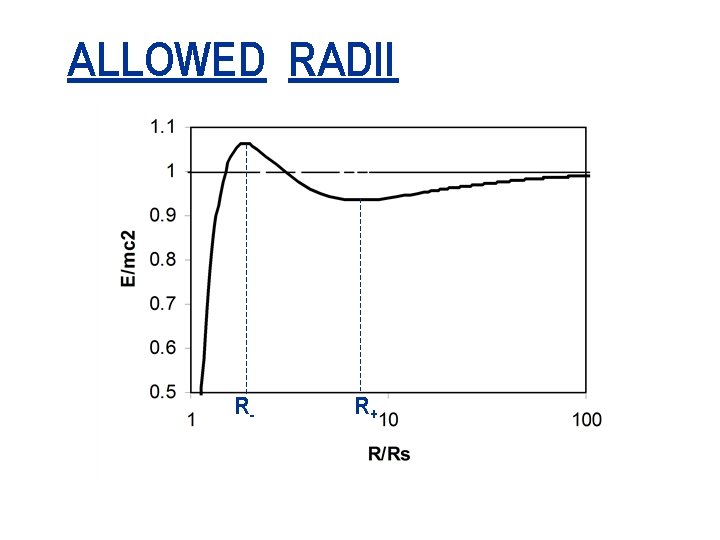
ALLOWED RADII R- R+

BOHR QUANTIZATION Using the Bohr quantization condition One obtains from The quantized allowed radii

ENERGY – CIRCULAR ORBITS From the quadratic resulting from the radial force equation One obtains Putting this into Results in

ENERGY QUANTIZATION From the energy One obtains the quantized energy levels where

References l l l Robert M. Wald, General Relativity (Univ of Chicago Press, 1984) pp 136 -148. Bernard F. Schutz, A First Course in General Relativity (Cambridge Univ Press, 1985) pp 274 -288. These slides http: //www. physics. ucok. edu/~wwilson
- Slides: 15