Body Centered Cubic BCC Crystal Structure Each atom

Body Centered Cubic (BCC) Crystal Structure • • Each atom has 8 nearest neighbors. Therefore, coordination number is 8. • Examples : Ø Chromium (a=0. 289 nm) Ø Iron (a=0. 287 nm) Ø Sodium (a=0. 429 nm) Figure 3. 4 a&b

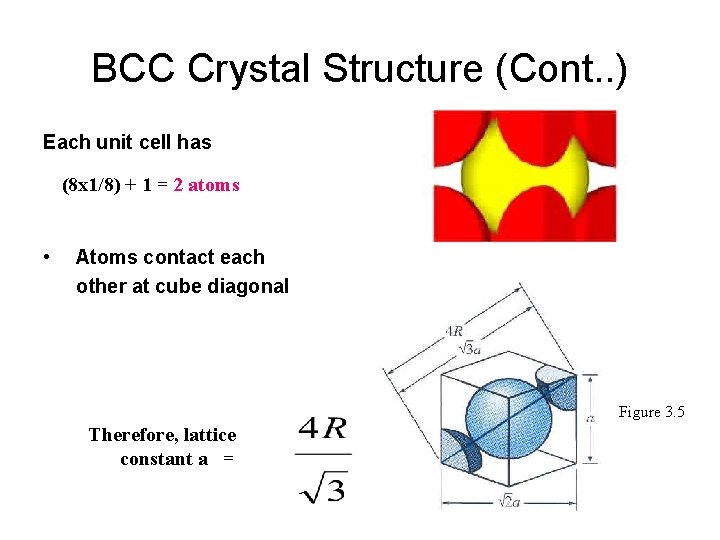
BCC Crystal Structure (Cont. . ) Each unit cell has (8 x 1/8) + 1 = 2 atoms • Atoms contact each other at cube diagonal Figure 3. 5 Therefore, lattice constant a =

Atomic Packing Factor of BCC Structure Atomic Packing Factor = Vatoms = V unit cell = a 3 = Volume of atoms in unit cell Volume of unit cell = 8. 373 R 3 = 12. 32 R 3 3 8. 723 R Therefore APF = 12. 32 R 3 = 0. 68

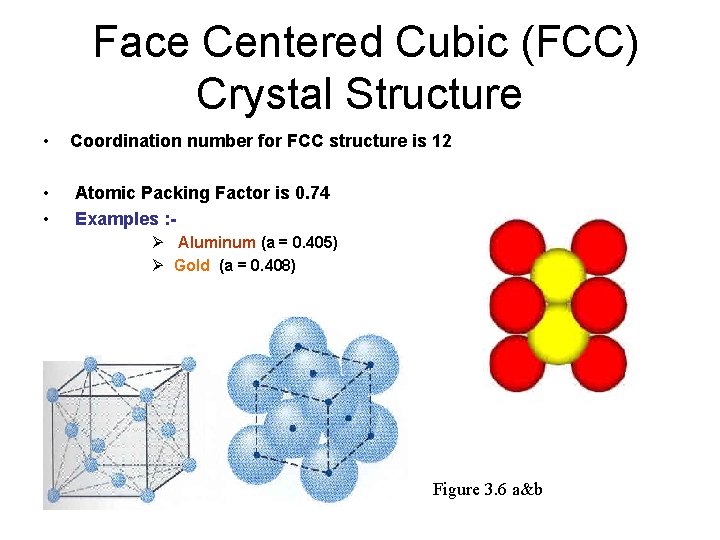
Face Centered Cubic (FCC) Crystal Structure • Coordination number for FCC structure is 12 • • Atomic Packing Factor is 0. 74 Examples : Ø Aluminum (a = 0. 405) Ø Gold (a = 0. 408) Figure 3. 6 a&b

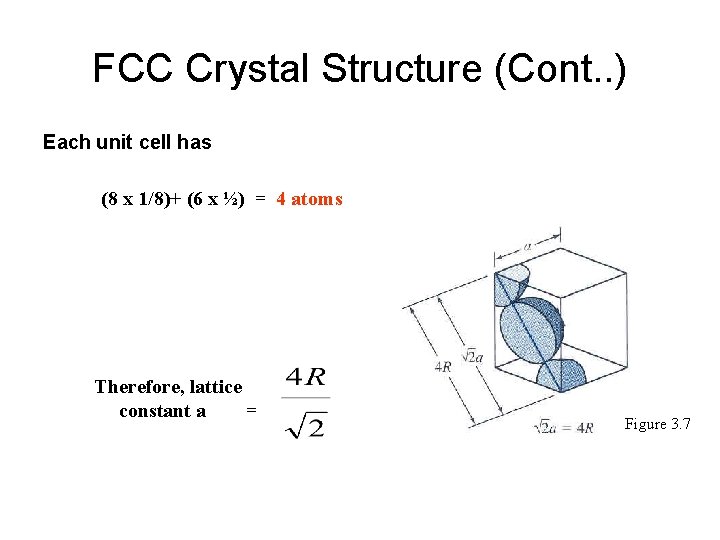
FCC Crystal Structure (Cont. . ) Each unit cell has (8 x 1/8)+ (6 x ½) = 4 atoms Therefore, lattice constant a = Figure 3. 7

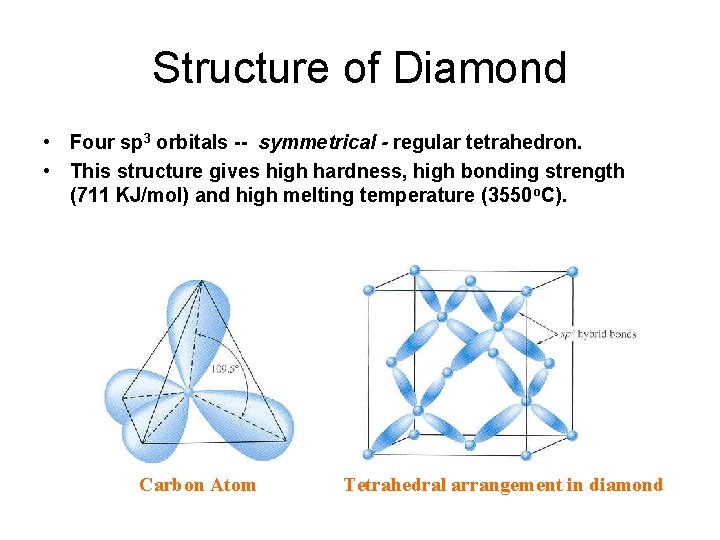
Structure of Diamond • Four sp 3 orbitals -- symmetrical - regular tetrahedron. • This structure gives high hardness, high bonding strength (711 KJ/mol) and high melting temperature (3550 o. C). Carbon Atom Tetrahedral arrangement in diamond

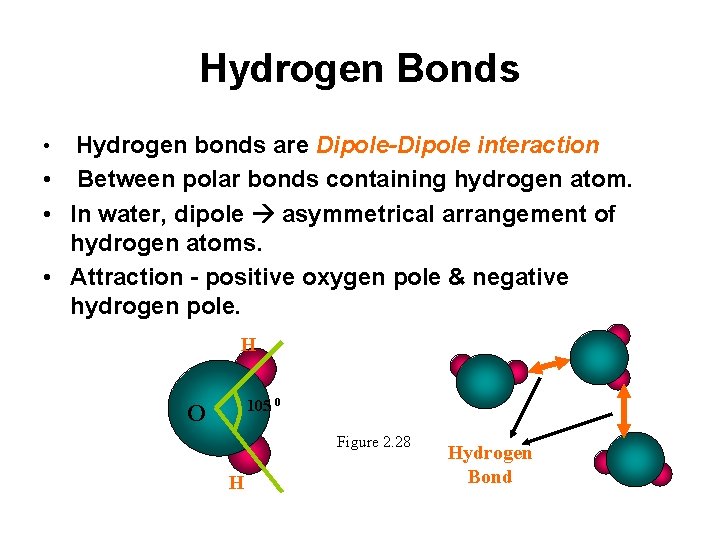
Hydrogen Bonds Hydrogen bonds are Dipole-Dipole interaction • Between polar bonds containing hydrogen atom. • In water, dipole asymmetrical arrangement of hydrogen atoms. • Attraction - positive oxygen pole & negative hydrogen pole. • H 105 0 O Figure 2. 28 H Hydrogen Bond

Permanent Dipoles • Dipoles that do not fluctuate with time are called Permanent dipoles. Ø Examples: - BP = -128 o. C BP = -14 o. C CH 4 CH 3 Cl Symmetrical Arrangement Of 4 C-H bonds Asymmetrical Tetrahedral arrangement No Dipole moment Creates Dipole

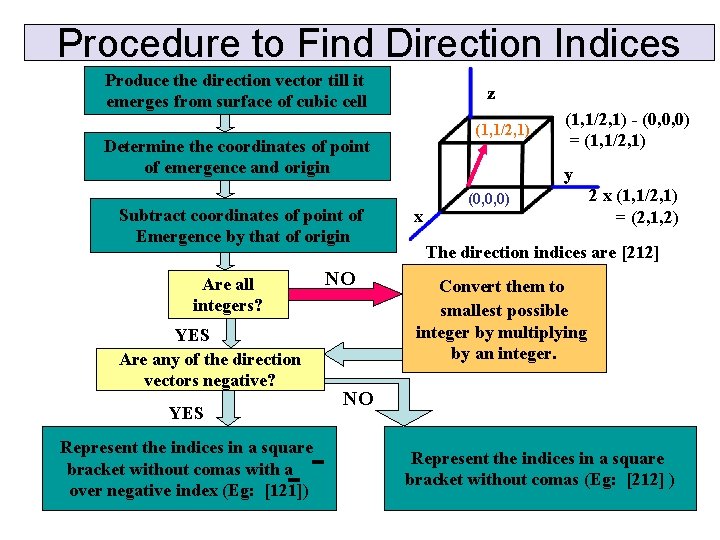
Procedure to Find Direction Indices Produce the direction vector till it emerges from surface of cubic cell z (1, 1/2, 1) Determine the coordinates of point of emergence and origin Subtract coordinates of point of Emergence by that of origin Are all integers? YES Are any of the direction vectors negative? YES Represent the indices in a square bracket without comas with a over negative index (Eg: [121]) NO (1, 1/2, 1) - (0, 0, 0) = (1, 1/2, 1) y x (0, 0, 0) 2 x (1, 1/2, 1) = (2, 1, 2) The direction indices are [212] Convert them to smallest possible integer by multiplying by an integer. NO Represent the indices in a square bracket without comas (Eg: [212] )

Miller Indices - Procedure Choose a plane that does not pass through origin Determine the x, y and z intercepts of the plane Find the reciprocals of the intercepts Fractions? Place a ‘bar’ over the Negative indices Clear fractions by multiplying by an integer to determine smallest set of whole numbers Enclose in parenthesis (hkl) where h, k, l are miller indices of cubic crystal plane for x, y and z axes. Eg: (111)

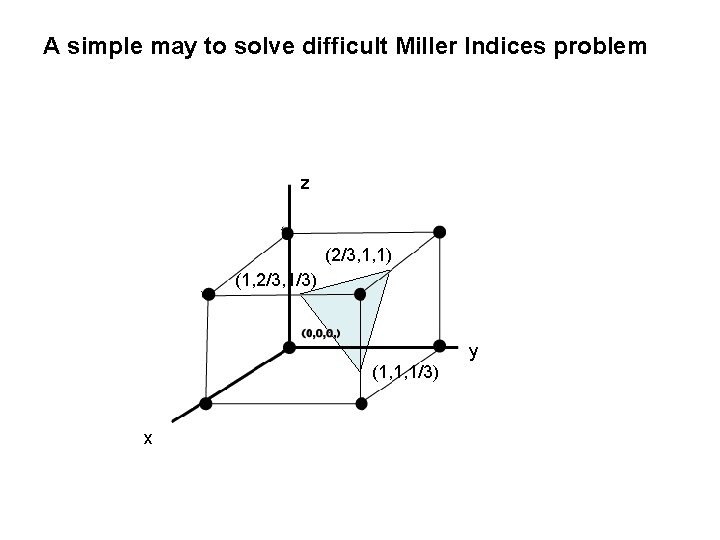
A simple may to solve difficult Miller Indices problem z (2/3, 1, 1) (1, 2/3, 1/3) y (1, 1, 1/3) x

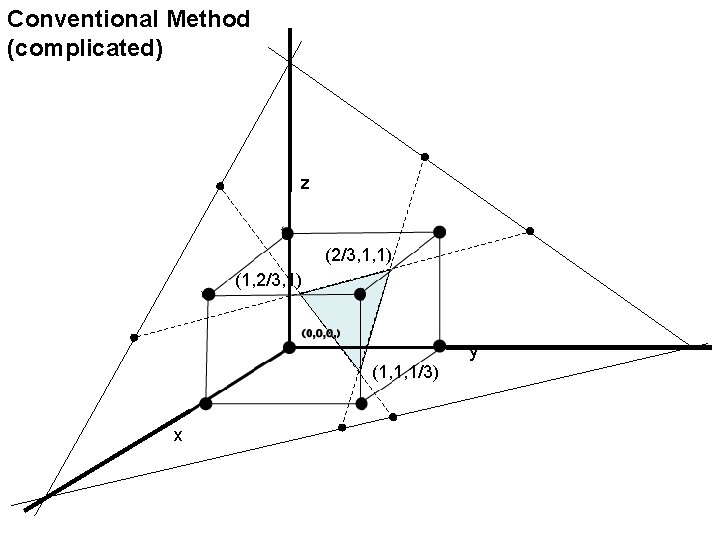
Conventional Method (complicated) z (2/3, 1, 1) (1, 2/3, 1) y (1, 1, 1/3) x

A Simple Method Use this equation h x 1 + k y 1 +l z 1 = h x 2 + k y 2 +l z 2 = h x 3 + k y 3 +l z 3 h + 2/3 k + l = 2/3 h + k + l = h + k +1/3 l 3 h + 2 k +3 l = 2 h + 3 k + 3 l = 3 h + 3 k + l 3 h + 2 k +3 l = 2 h + 3 k + 3 l h =k h = 2 l h = k = 2 l If l = 1 h=2, k=2, l=1 (221)

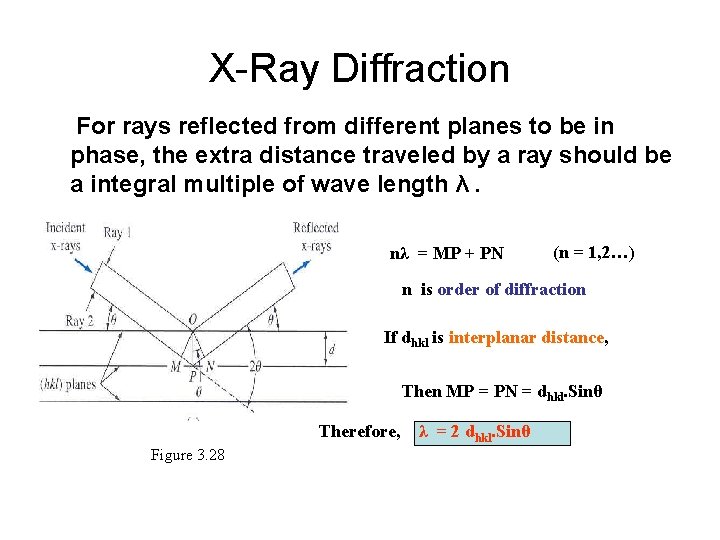
X-Ray Diffraction For rays reflected from different planes to be in phase, the extra distance traveled by a ray should be a integral multiple of wave length λ. nλ = MP + PN (n = 1, 2…) n is order of diffraction If dhkl is interplanar distance, Then MP = PN = dhkl. Sinθ Therefore, Figure 3. 28 λ = 2 dhkl. Sinθ

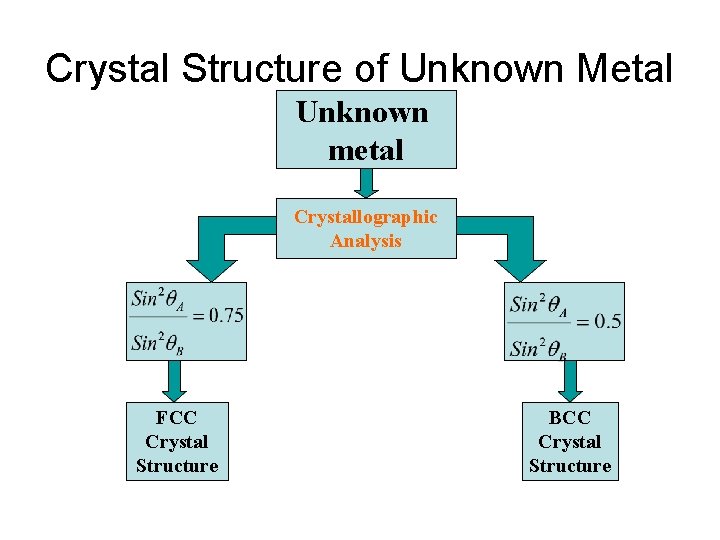
Crystal Structure of Unknown Metal Unknown metal Crystallographic Analysis FCC Crystal Structure BCC Crystal Structure

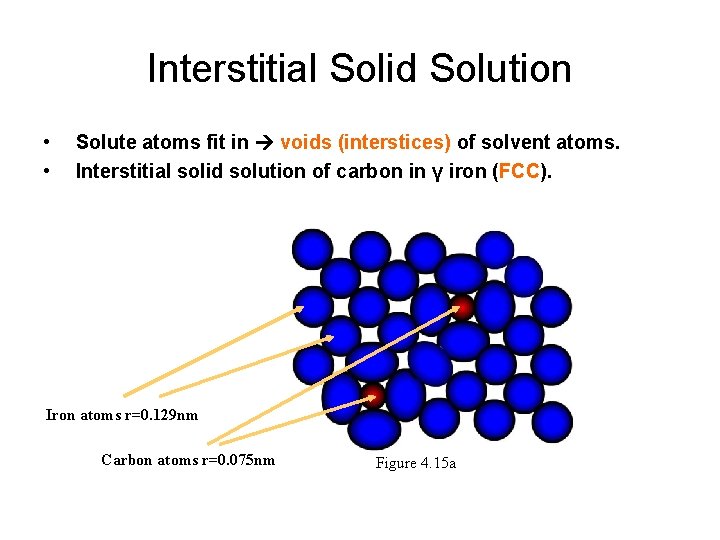
Interstitial Solid Solution • • Solute atoms fit in voids (interstices) of solvent atoms. Interstitial solid solution of carbon in γ iron (FCC). Iron atoms r=0. 129 nm Carbon atoms r=0. 075 nm Figure 4. 15 a

Stress and Strain in Metals • Metals undergo deformation under uniaxial tensile force. • Elastic deformation: Metal returns to its original dimension after tensile force is removed. • Plastic deformation: The metal is deformed to such an extent such that it cannot return to its original dimension 6 -10 Elastic deformation Plastic deformation

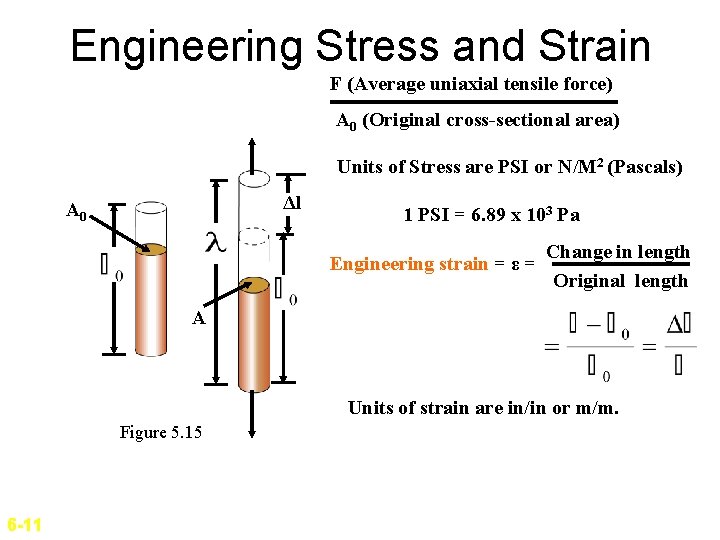
Engineering Stress and Strain F (Average uniaxial tensile force) A 0 (Original cross-sectional area) Engineering stress σ = Δl A 0 Units of Stress are PSI or N/M 2 (Pascals) 1 PSI = 6. 89 x 103 Pa Engineering strain = ε = Change in length Original length A Units of strain are in/in or m/m. Figure 5. 15 6 -11

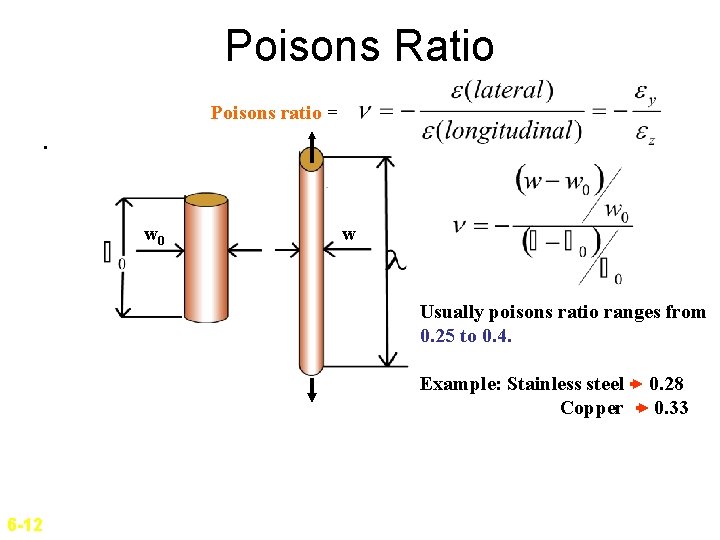
Poisons Ratio Poisons ratio =. w 0 w Usually poisons ratio ranges from 0. 25 to 0. 4. Example: Stainless steel Copper 6 -12 0. 28 0. 33

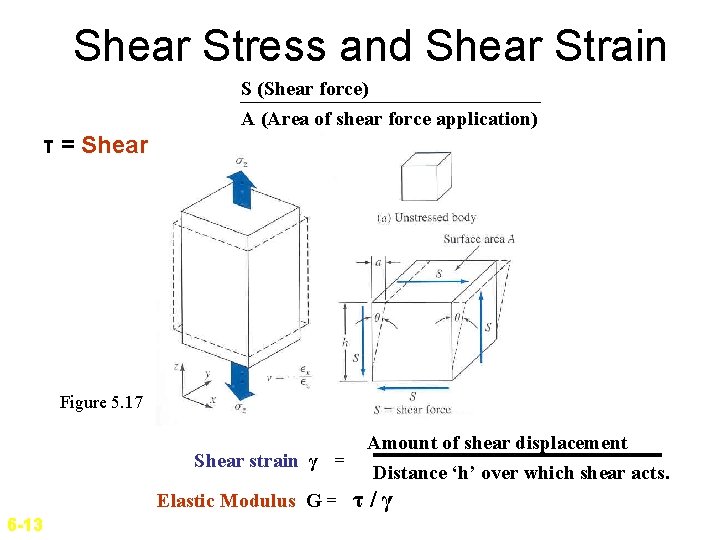
Shear Stress and Shear Strain S (Shear force) A (Area of shear force application) τ = Shear stress = Figure 5. 17 Shear strain γ = Elastic Modulus G = 6 -13 Amount of shear displacement Distance ‘h’ over which shear acts. τ/γ

Yield Strength • Yield strength is strength at which metal or alloy show significant amount of plastic deformation. • 0. 2% offset yield strength is that strength at which 0. 2% plastic deformation takes place. • Construction line, starting at 0. 2% strain and parallel to elastic region is drawn to find 0. 2% offset yield strength. 6 -18

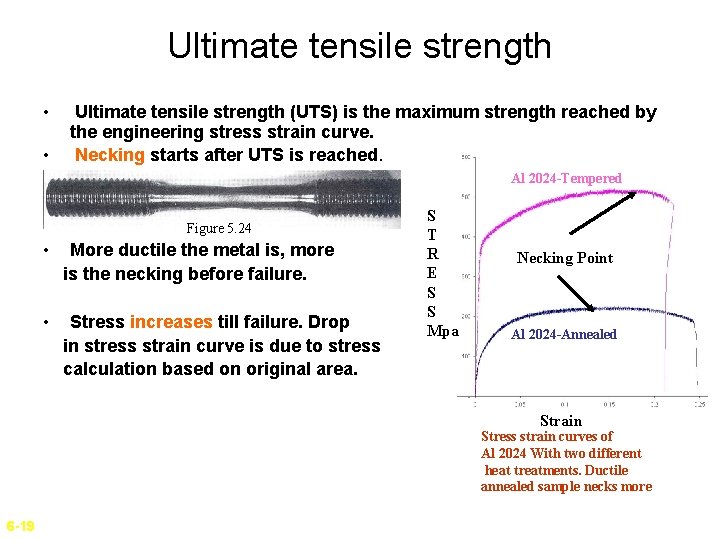
Ultimate tensile strength • • Ultimate tensile strength (UTS) is the maximum strength reached by the engineering stress strain curve. Necking starts after UTS is reached. Al 2024 -Tempered Figure 5. 24 • More ductile the metal is, more is the necking before failure. • Stress increases till failure. Drop in stress strain curve is due to stress calculation based on original area. S T R E S S Mpa Necking Point Al 2024 -Annealed Strain Stress strain curves of Al 2024 With two different heat treatments. Ductile annealed sample necks more 6 -19

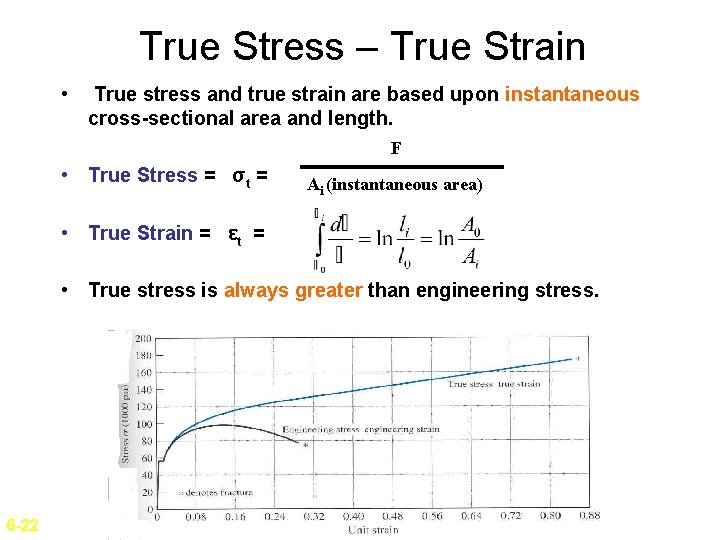
True Stress – True Strain • True stress and true strain are based upon instantaneous cross-sectional area and length. F • True Stress = σt = Ai (instantaneous area) • True Strain = εt = • True stress is always greater than engineering stress. 6 -22

Gibbs Phase Rule • P+F = C+2 P = number of phases that coexist in a system C = Number of components F = Degrees of freedom • For pure water, at triple point, 3 phases coexist. • There is one component (water) in the system. • Therefore 3 + F = 1 + 2 F = 0. • Degrees of freedom indicate number of variables that can be changed without changing number of phases. 8 -4

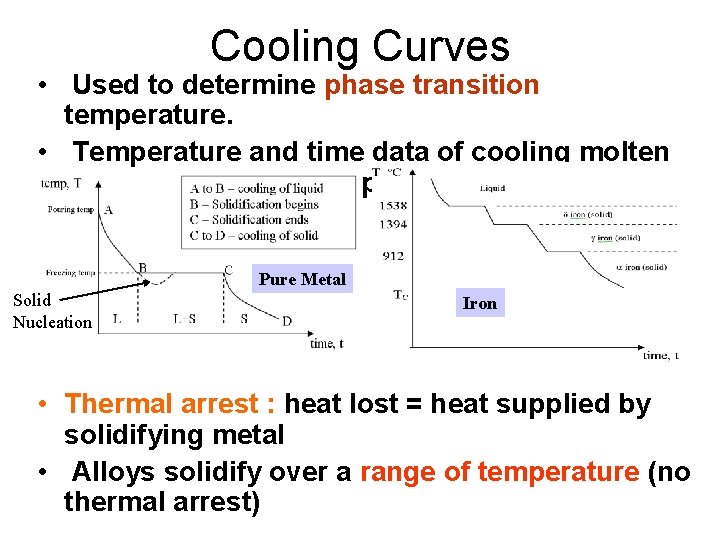
Cooling Curves • Used to determine phase transition temperature. • Temperature and time data of cooling molten metal is recorded and plotted. Pure Metal Solid Nucleation Iron • Thermal arrest : heat lost = heat supplied by solidifying metal • Alloys solidify over a range of temperature (no thermal arrest)

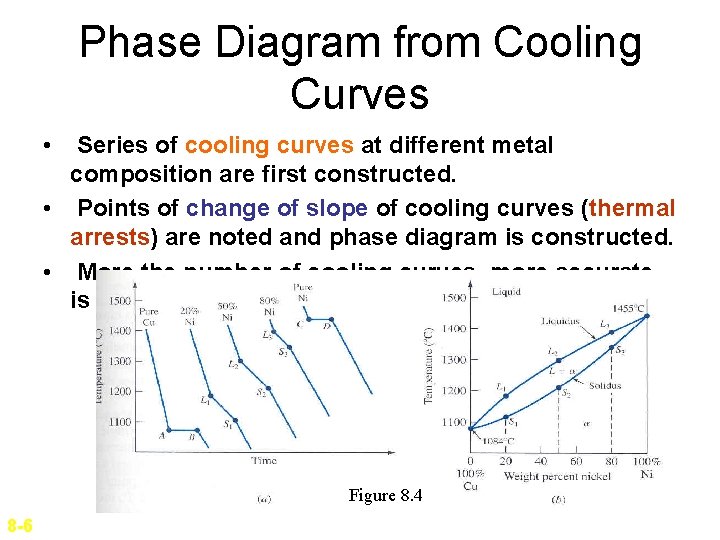
Phase Diagram from Cooling Curves • Series of cooling curves at different metal composition are first constructed. • Points of change of slope of cooling curves (thermal arrests) are noted and phase diagram is constructed. • More the number of cooling curves, more accurate is the phase diagram. Figure 8. 4 8 -6

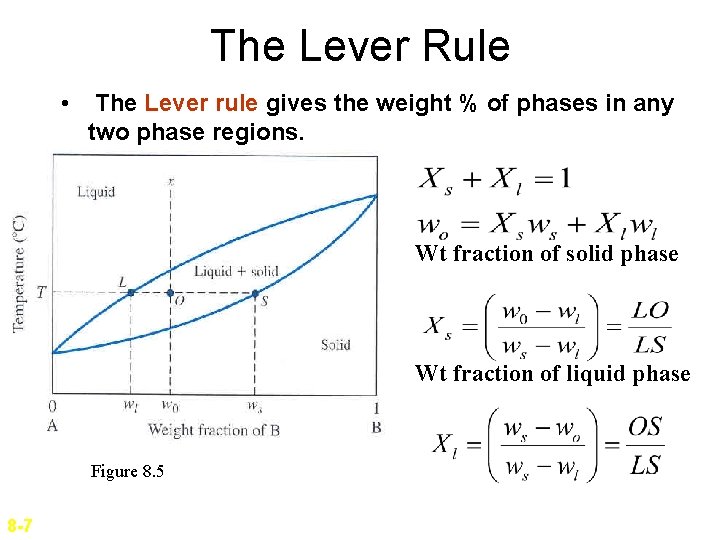
The Lever Rule • The Lever rule gives the weight % of phases in any two phase regions. Wt fraction of solid phase Wt fraction of liquid phase Figure 8. 5 8 -7

Non Equilibrium Solidification of Alloys • Fast rate of cooling (non-equilibrium) gives rise to cored structure. • Rapid cooling delays solidification. • Homogenization: Cast ingots heated to elevated temperature to eliminate cored structure. • Temperature of homogenization must be lower than lowest melting point of any of the alloy components. Figure 8. 7 Figure 8. 8

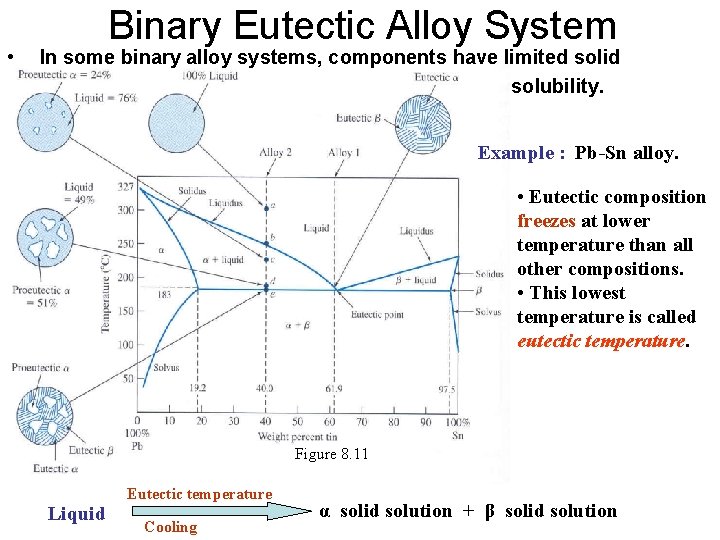
• Binary Eutectic Alloy System In some binary alloy systems, components have limited solid solubility. Example : Pb-Sn alloy. • Eutectic composition freezes at lower temperature than all other compositions. • This lowest temperature is called eutectic temperature. Figure 8. 11 Liquid Eutectic temperature Cooling α solid solution + β solid solution

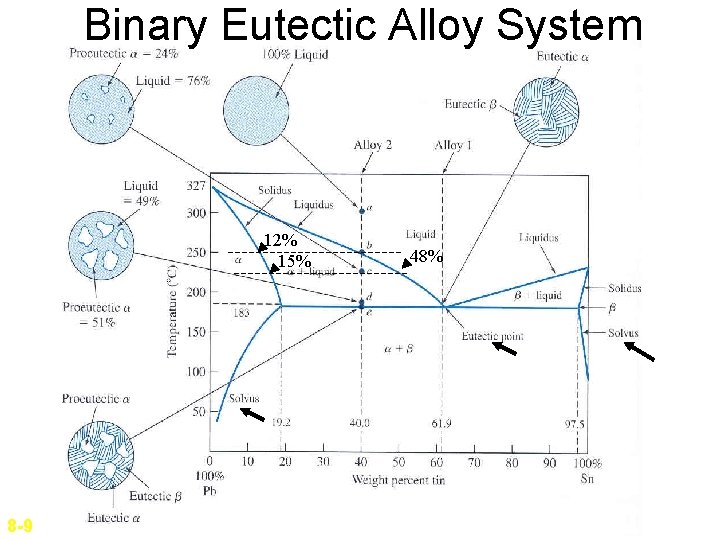
Binary Eutectic Alloy System 12% 15% 8 -9 48%