Blocking Confounding in the 2 k Factorial Design

Blocking & Confounding in the 2 k Factorial Design • Text reference, Chapter 7 • Blocking is a technique for dealing with controllable nuisance variables • Two cases are considered – Replicated designs – Unreplicated designs 1

Blocking a Replicated Design • This is the same scenario discussed previously (Chapter 5, Section 5 -6) • If there are n replicates of the design, then each replicate is a block • Each replicate is run in one of the blocks (time periods, batches of raw material, etc. ) • Runs within the block are randomized 2

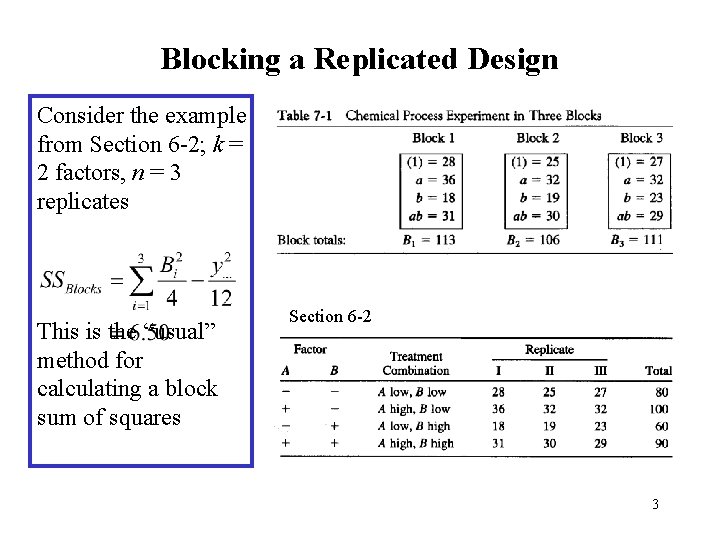
Blocking a Replicated Design Consider the example from Section 6 -2; k = 2 factors, n = 3 replicates This is the “usual” method for calculating a block sum of squares Section 6 -2 3

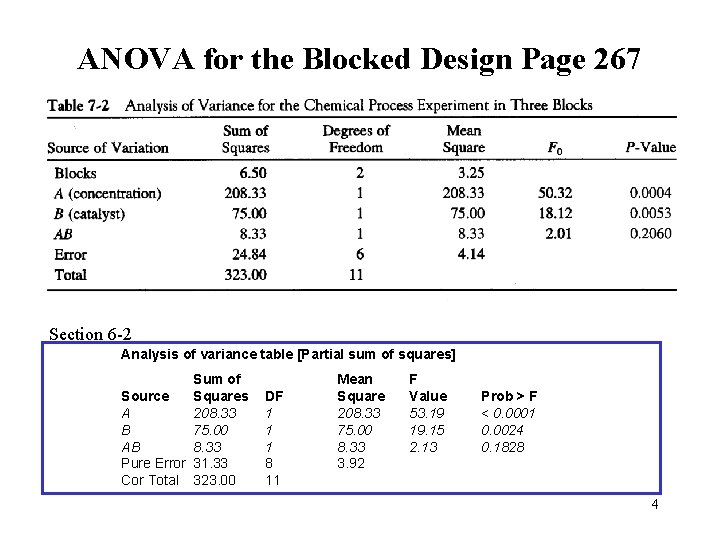
ANOVA for the Blocked Design Page 267 Section 6 -2 Analysis of variance table [Partial sum of squares] Sum of Source Squares A 208. 33 B 75. 00 AB 8. 33 Pure Error 31. 33 Cor Total 323. 00 DF 1 1 1 8 11 Mean Square 208. 33 75. 00 8. 33 3. 92 F Value 53. 19 19. 15 2. 13 Prob > F < 0. 0001 0. 0024 0. 1828 4

Confounding in Blocks • Now consider the unreplicated case • Clearly the previous discussion does not apply, since there is only one replicate • To illustrate, consider the situation of Example 6 -2, Page 228 • This is a 24, n = 1 replicate 5

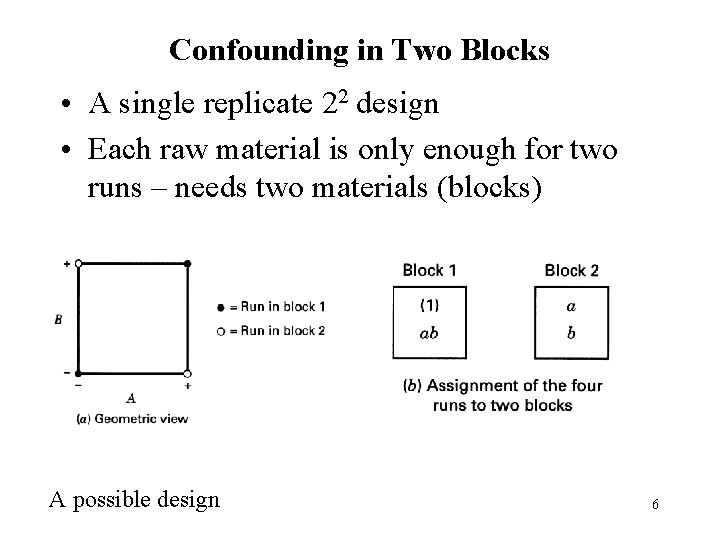
Confounding in Two Blocks • A single replicate 22 design • Each raw material is only enough for two runs – needs two materials (blocks) A possible design 6

Confounding in Two Blocks • Estimating effects A = ½[ab + a – b – (1)] B = ½[ab + b – a – (1)] AB = ½[ab + (1) – a – b] 7

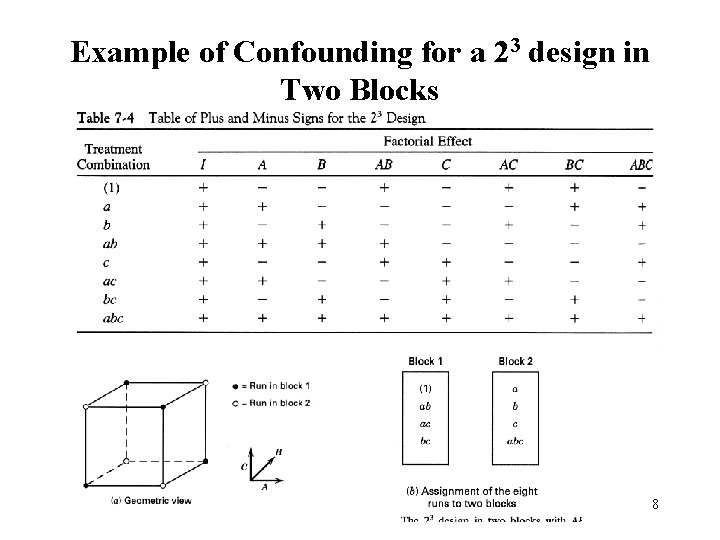
Example of Confounding for a 23 design in Two Blocks 8

Other Methods of Constructing the Blocks • Use of a defining contrast L = a 1 x 1 + a 2 x 2 + a 3 x 3 + …+ akxk xi: level of the ith factor in a particular treatment combination (0 or 1) ai: exponent appearing on the ith factor in the effect to be confounded (0 or 1) • Treatment combinations that produce the same value of L (mod 2) will be placed in the same block 9

Other Methods of Constructing the Blocks • Example: a 23 design with ABC confounded with blocks a 1 = 1; a 2 = 1; a 3 = 1 x 1 A; x 2 B; x 3 C; L = x 1 + x 2 + x 3 (1) ab ac bc 000: 110: 101: 011: L=0=0 L=2=0 a b c abc 100: 010: 001: 111: L=1=1 L=3=1 10

Estimation of Error • Example: a 23 design, must be run in two blocks with ABC confounded, four replicates 11

• It would be better if blocks are designed differently in each replicate, to confound a different effect in each replicate – partial confounding 12

Example of Unreplicated Design (Ex. 7 -2) • Response: filtration rate of a resin • Factors: A = temperature, B = pressure, C = mole ratio/concentration, D= stirring rate • One batch of raw material is only enough for 8 runs. Two materials are required. • ABCD is chosen for confounding. • L = x 1 + x 2 + x 3 + x 4 13

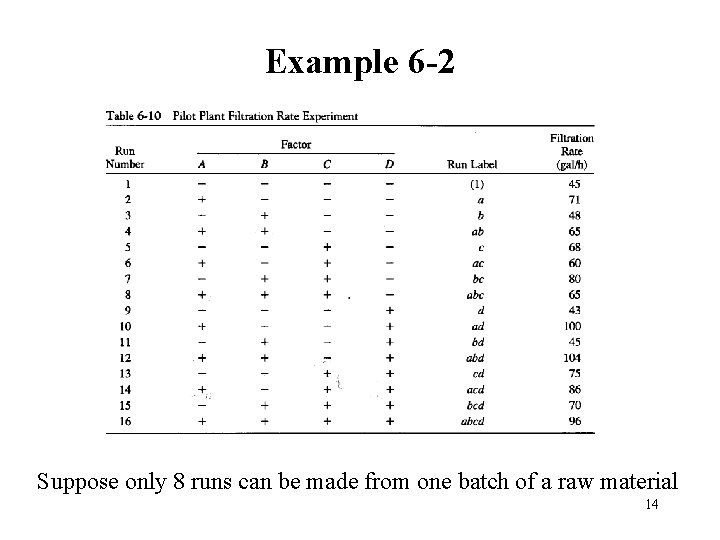
Example 6 -2 Suppose only 8 runs can be made from one batch of a raw material 14

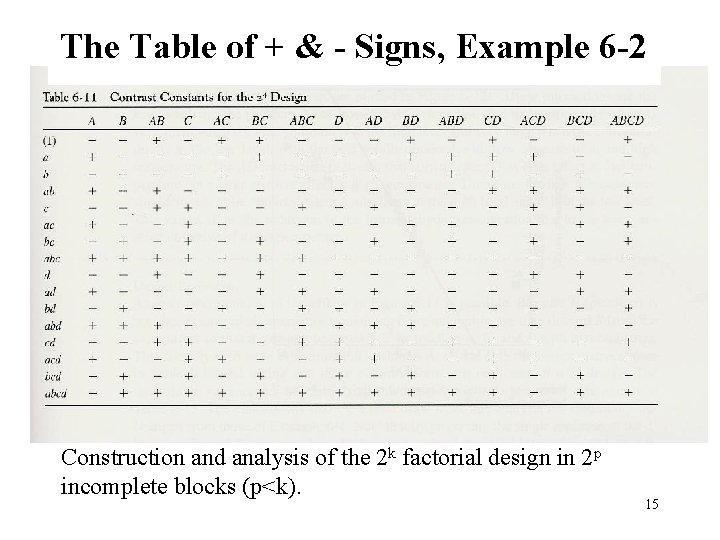
The Table of + & - Signs, Example 6 -2 Construction and analysis of the 2 k factorial design in 2 p incomplete blocks (p<k). 15

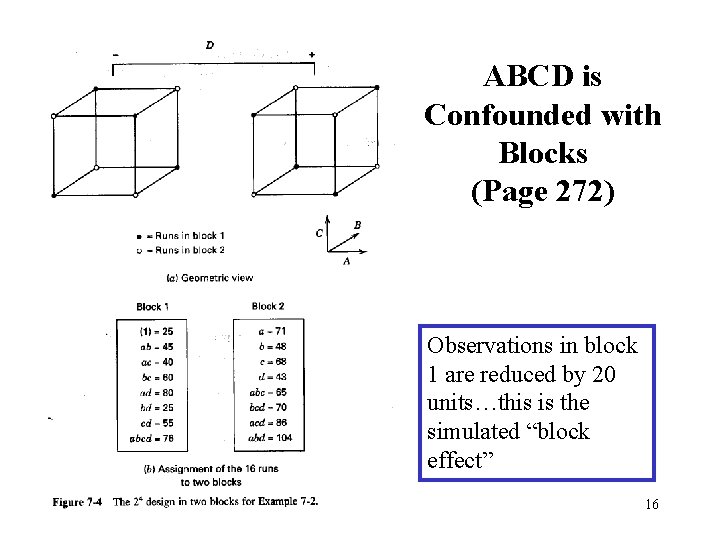
ABCD is Confounded with Blocks (Page 272) Observations in block 1 are reduced by 20 units…this is the simulated “block effect” 16

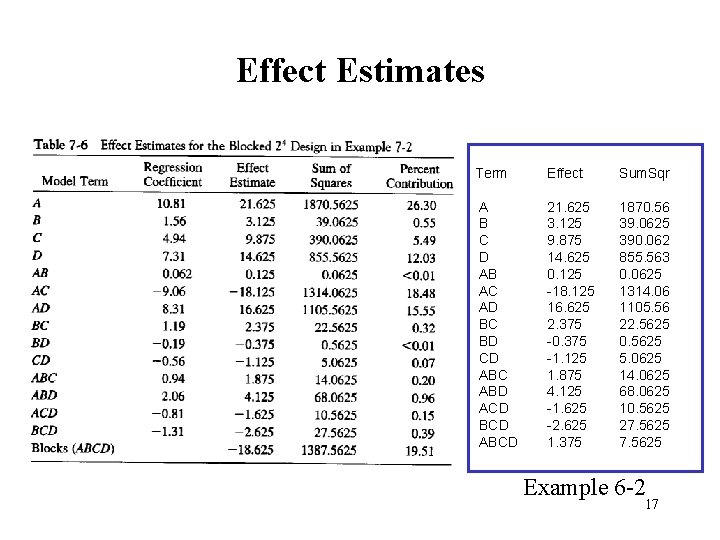
Effect Estimates Term Effect Sum. Sqr A B C D AB AC AD BC BD CD ABC ABD ACD BCD ABCD 21. 625 3. 125 9. 875 14. 625 0. 125 -18. 125 16. 625 2. 375 -0. 375 -1. 125 1. 875 4. 125 -1. 625 -2. 625 1. 375 1870. 56 39. 0625 390. 062 855. 563 0. 0625 1314. 06 1105. 56 22. 5625 0. 5625 5. 0625 14. 0625 68. 0625 10. 5625 27. 5625 Example 6 -2 17

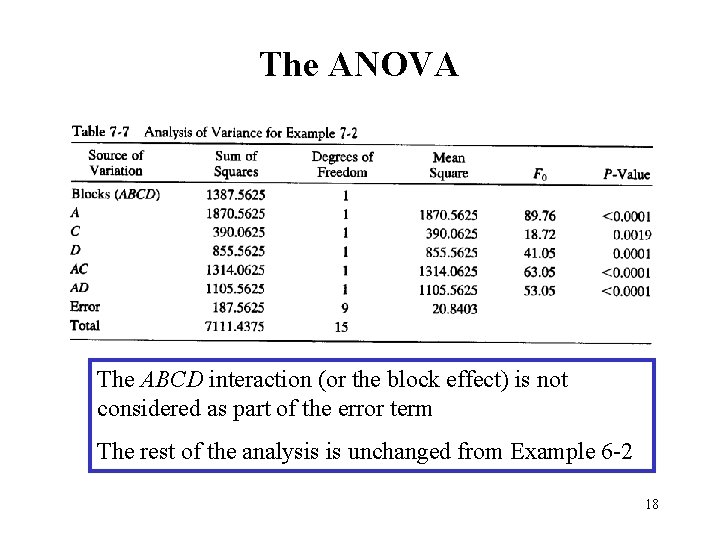
The ANOVA The ABCD interaction (or the block effect) is not considered as part of the error term The rest of the analysis is unchanged from Example 6 -2 18