BLOCK LU DECOMPOSITION EXPLAINED Keiran OHaire Introduction Method

BLOCK LU DECOMPOSITION: EXPLAINED Keiran O’Haire

Introduction Method for performing LU decomposition on large matrices Requires more calculations Faster due to memory locality

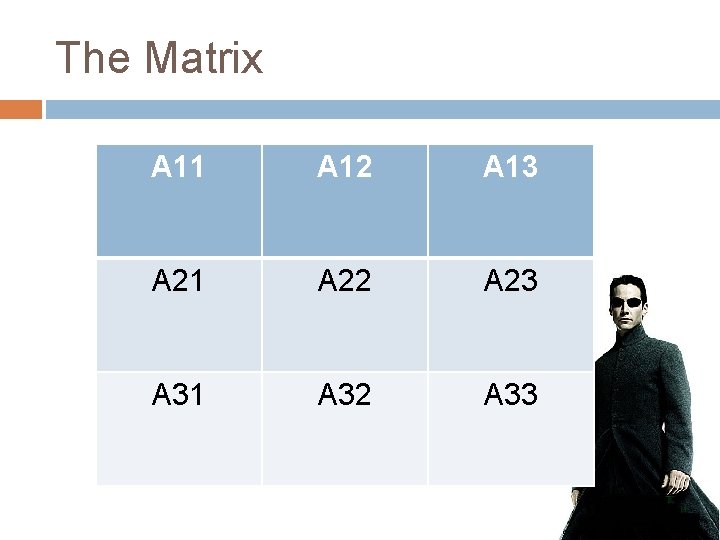
The Matrix A 11 A 12 A 13 A 21 A 22 A 23 A 31 A 32 A 33

Notes Each of the boxes represent sub matrices of the original matrix The sub matrices’ size are determined by the block size Example: sub matrix with block size 4 4 2 1 8

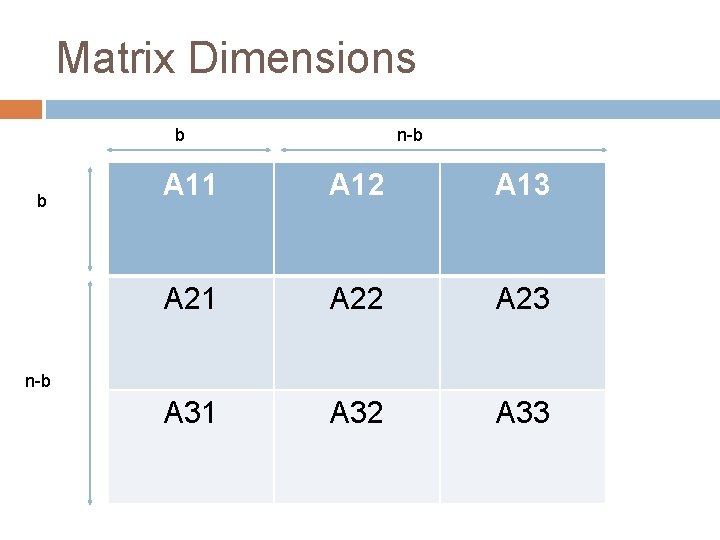
Matrix Dimensions b b n-b A 11 A 12 A 13 A 21 A 22 A 23 A 31 A 32 A 33 n-b

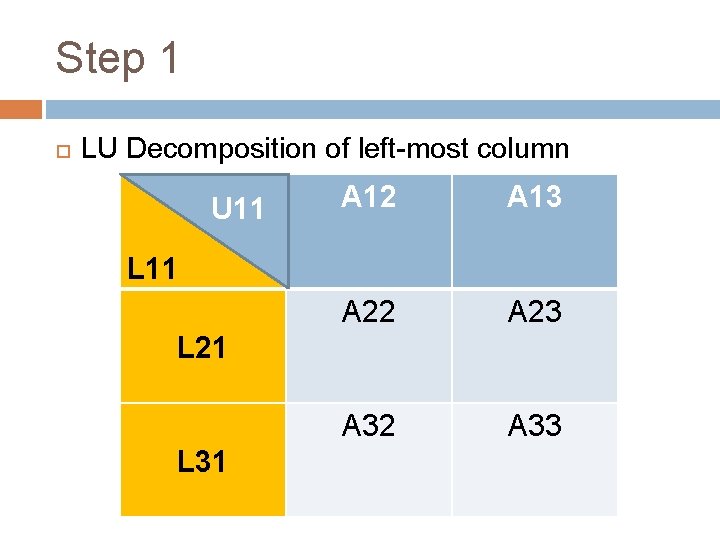
Step 1 LU Decomposition of left-most column U 11 A 12 A 13 A 22 A 23 A 32 A 33 L 11 L 21 L 31

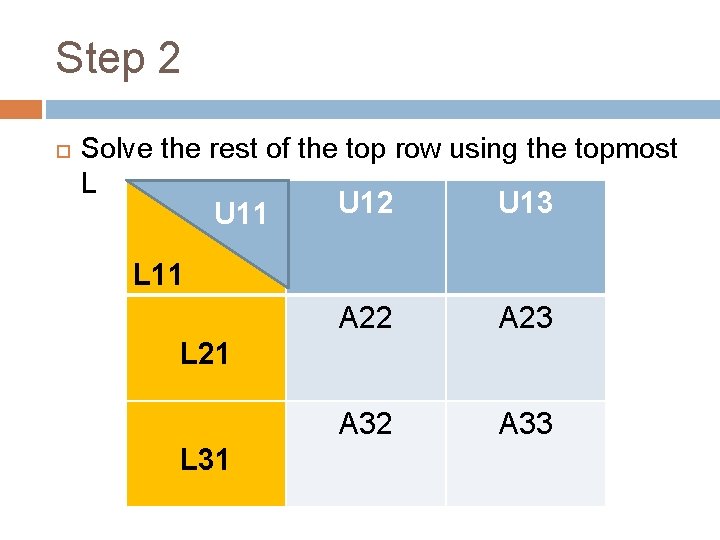
Step 2 Solve the rest of the top row using the topmost L U 12 U 13 U 11 L 11 A 22 A 23 A 32 A 33 L 21 L 31

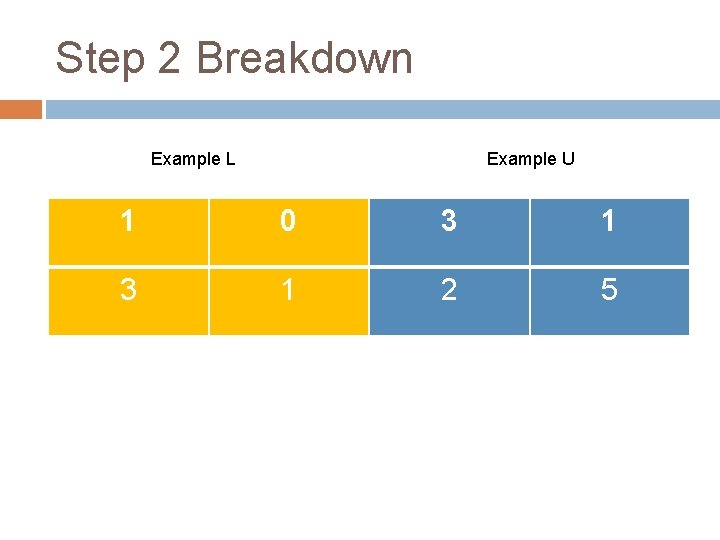
Step 2 Breakdown Example L Example U 1 0 3 1 2 5

Column Version Use one column at a time from the matrix you wish to solve 1 0 3 3 1 2

Column Version Cont’d The result! 3 -7

Column Version Cont’d Now insert the next column Repeat until all columns are solved 1 0 1 3 1 5

Row Version Same matrices as before, but this time were doing rows The version is dependent on the language you are using, such as C or FORTRAN due to array orientation 1 0 3 1 2 5

Row Version Cont’d This time, solve each of these (one cell at a time) in a row. i. e. solve [1 0] = [3] Clearly, for the first, x 1=3, and for the second, x 1=1 1 0 3 1

Row Version Cont’d These calculated x’s are now used in the next row. i. e. , 3(x 1=3) + x 2 = 2, x 2=-7 Then, 3(x 1=1) + x 2 = 5, x 2=2 1 0 3 1 2 5

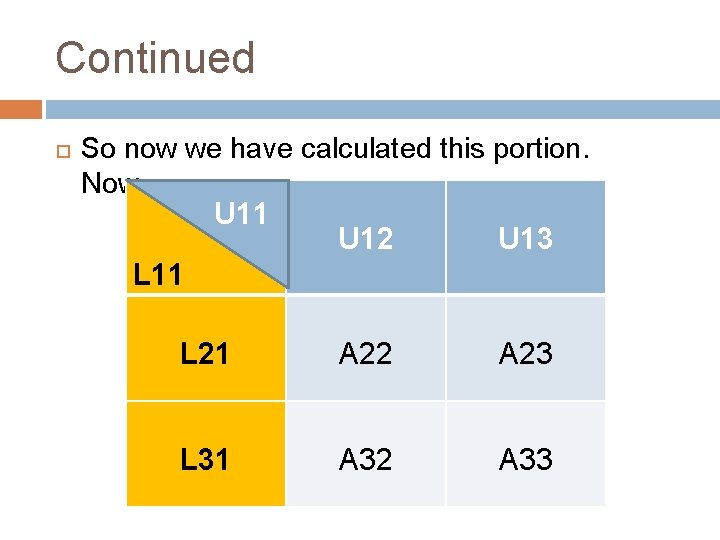
Continued So now we have calculated this portion. Now…. . U 11 U 12 U 13 L 11 L 21 A 22 A 23 L 31 A 32 A 33

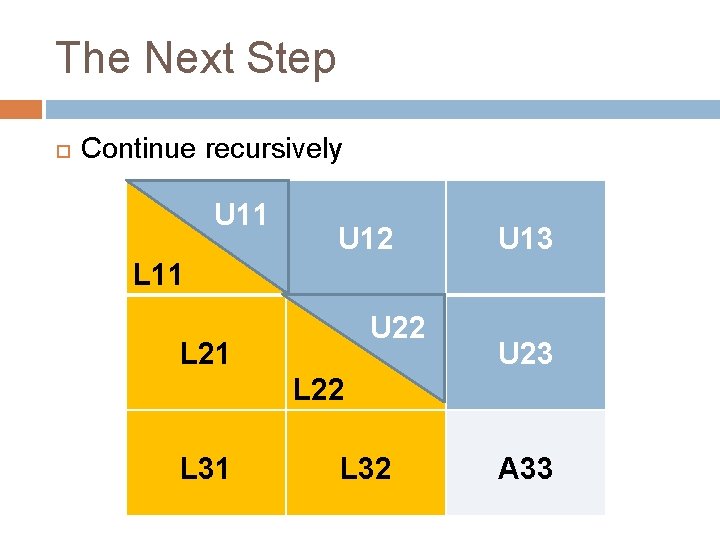
The Next Step Continue recursively U 11 U 12 U 13 L 11 U 22 L 21 U 23 L 22 L 31 L 32 A 33

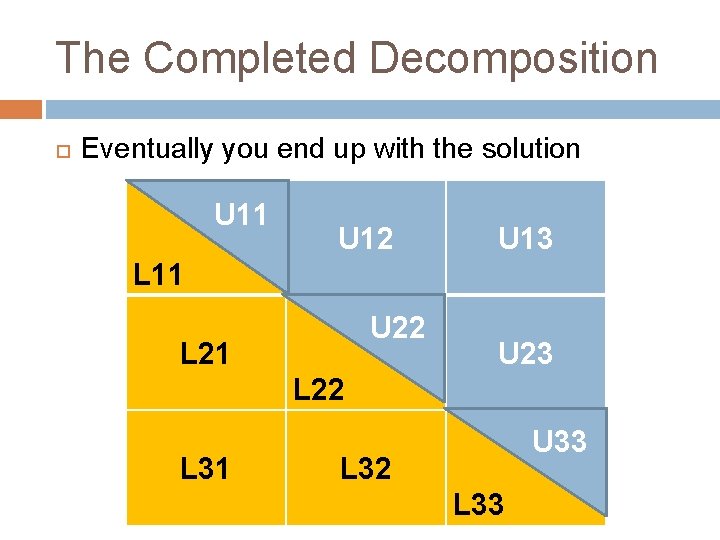
The Completed Decomposition Eventually you end up with the solution U 11 U 12 U 13 L 11 U 22 L 21 U 23 L 22 L 31 U 33 L 32 L 33

Questions?