Block Floating Point Interval ALU for Digital Signal

Block Floating Point Interval ALU for Digital Signal Processing Sandeep Hattangady, William Edmonson, Winser Alexander September 30, 2008 Hi. Per DSP Lab, North Carolina State University

Outline q Introduction q Background q Architecture q Results q Conclusions and Future Work q References

Outline q Introduction q Background q Architecture q Results q Conclusion s and Future Work q References

Introduction Problem Statement o To provide reliable arithmetic for embedded systems. n Low power n Small footprint n Real-time computing o Applications n n Digital signal processing & Control Fuzzy systems q Adaptive filtering q Decision systems

Introduction Problem Statement q Fixed point implementations face overflow due to small dynamic range Upper Bound Overflow in an interval Summation Bound Build a fixed point interval ALU whose arithmetic Lower stays reliable Lower Bound even in the presence of overflow. Upper Bound Two’s complement format Q 7. 8 input data Q 15. 0 output data Overflow leads to unreliable interval arithmetic!

Introduction Problem Solution o Use Block Floating Point (BFP) arithmetic to achieve higher dynamic range over that of conventional fixed point architectures o Handle overflows using Conditional Block Floatingpoint Scaling (CBFS) scheme

Outline q Introduction q Background q Architecture q Results q Conclusions and Future Work q References
![Previous Work q Dedicated fixed point interval ALU [Ruchir 2006] § The only fixed Previous Work q Dedicated fixed point interval ALU [Ruchir 2006] § The only fixed](http://slidetodoc.com/presentation_image_h2/56f3f1853b6a3d5717855cc7b3e40fd1/image-8.jpg)
Previous Work q Dedicated fixed point interval ALU [Ruchir 2006] § The only fixed point interval ALU implementation. § No scheme in place to handle overflow. q Block Floating Point arithmetic § § § Digital filters [Oppenheim 1970] Fast Fourier Transform (FFT) processors Fast Hartley Transform (FHT) processors [Bidet 1995] [Erickson 1992] q Commercial Fixed point DSPs with BFP support * ADSP-21 xx * TMS 320 C 64 x * NEC u. PD 7701 x * TMS 320 C 54 x * Oak DSP Core * Lucent DSP 16 xx * SGS Thomson D 950 -Core
![Background Criteria for Reliable IA q Correctness : [Van Emden 2001] An interval operation Background Criteria for Reliable IA q Correctness : [Van Emden 2001] An interval operation](http://slidetodoc.com/presentation_image_h2/56f3f1853b6a3d5717855cc7b3e40fd1/image-9.jpg)
Background Criteria for Reliable IA q Correctness : [Van Emden 2001] An interval operation is correct when the output interval contains results of all point-wise evaluations based on values from the argument intervals. For ex: [1, 2] + [3, 4] = [4, 6] q Totality : A total interval operation is one that is defined for all possible input arguments. For ex : We provide only division by powers of 2 eliminating divide-by-0 error. q Closedness : A closed interval operation indicates that the output interval is obtained on the same space as that of the input intervals. For example, interval operations on intervals defined on the real space R always yields an output interval on the space R. q Optimality : An optimal interval operation does not perform any overestimation and its bounds are the most optimized ones for the type of representation chosen. q Efficiency : The term efficiency is defined with respect to the implementation of interval arithmetic in hardware.

Background Thought Process Fixed point implementations q Lower design complexity q Small dynamic range Floating Point implementations q Higher design complexity q Large dynamic range Block Floating Point representation Associate a group of fixed point values with a common exponent term
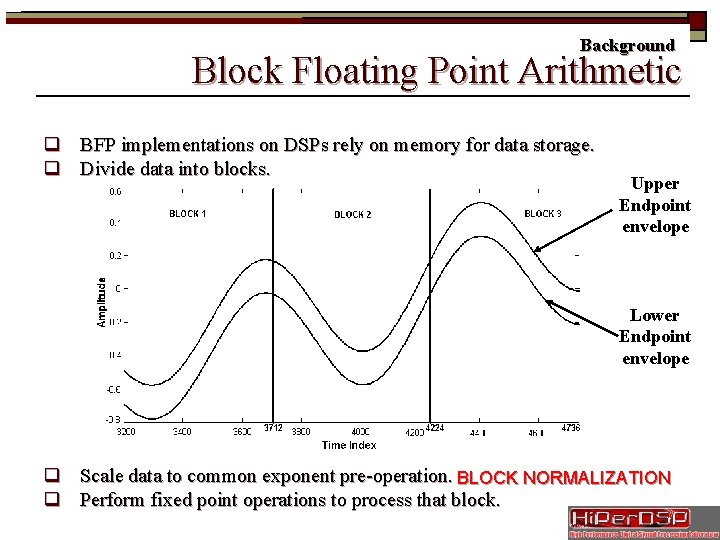
Background Block Floating Point Arithmetic q BFP implementations on DSPs rely on memory for data storage. q Divide data into blocks. Upper Endpoint envelope Lower Endpoint envelope q Scale data to common exponent pre-operation. BLOCK NORMALIZATION q Perform fixed point operations to process that block.
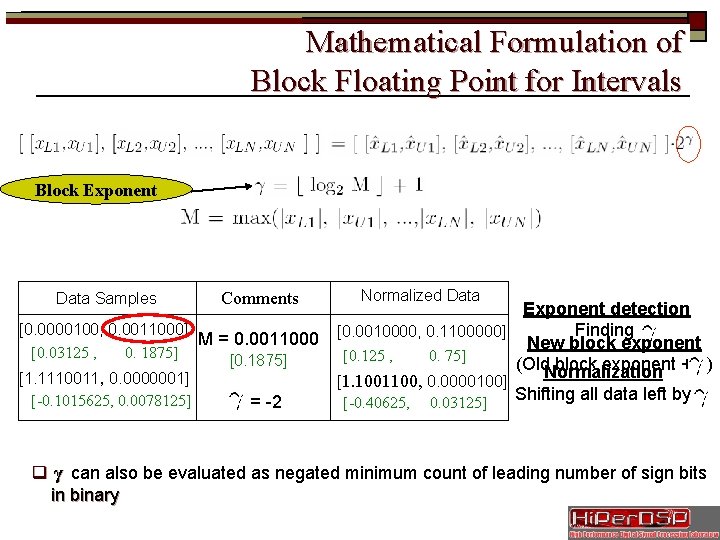
Mathematical Formulation of Block Floating Point for Intervals Block Exponent Data Samples Comments [0. 0000100, 0. 0011000] M = 0. 0011000 [0. 03125 , 0. 1875] [1. 1110011, 0. 0000001] [-0. 1015625, 0. 0078125] = -2 Normalized Data Exponent detection Finding [0. 0010000, 0. 1100000] New block exponent [0. 125 , 0. 75] (Old. Normalization block exponent + ) [1. 1001100, 0. 0000100] Shifting all data left by [-0. 40625, 0. 03125] q γ can also be evaluated as negated minimum count of leading number of sign bits in binary

Design Specifications Handling Fixed Point Overflows Conditional Block Floating-point Scaling (CBFS) o Overflow mainly associated with Addition operation o CBFS based on correcting errors o Procedure: n Perform operation n Check if overflow occurred n If it did, scale down the result by a factor of 2 Increment output block exponent n If it didn’t overflow, retain result Output block exponent is same as input block exponent

Design Specifications Rounding o Outward Rounding n Output interval must meet correctness n Retain the rounding scheme from IALU [Ruchir 2006] q Truncate lower endpoint by discarding higher precision bits q Add the OR-ed result of the discarded bits to round the result to +∞. q Rounding to +∞ can cause overflow. q Example of Rounding 32 -bit to +∞ to yield 16 -bit: 7 FFF XXXX (hex) where XXXX is not 0000 (hex) Rounding to +∞yields 7 FFF + 1 = 8000 (hex) q Correct by sending out 4000 (hex), increment output block exponent. Referred to as Special case of Rounding.

Outline q Introduction q Background q Architecture q Results q Conclusions and Future Work q References
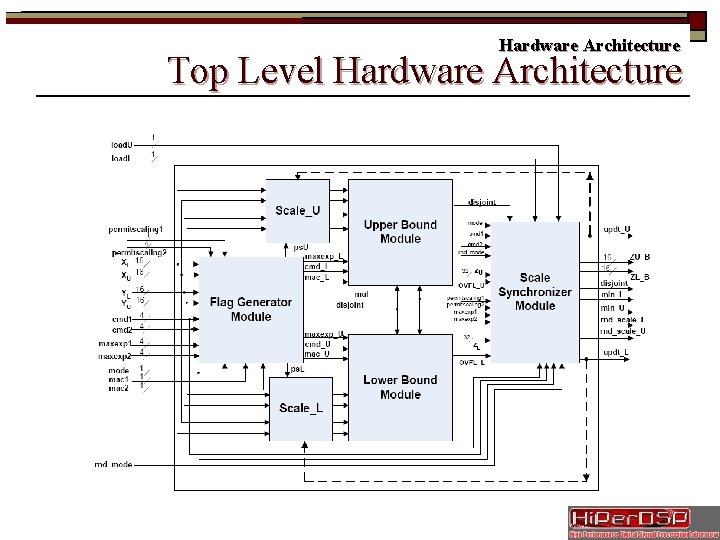
Hardware Architecture Top Level Hardware Architecture

Hardware Architecture Slide 17/35 Flag Generator 1. Identify case of Multiplication using flag-combinations 2. Distributing Commands to Lower and Upper Bound modules 3. Generating Disjoint Signal Compare (XL with YU) ; (XU with YL) Set ‘disjoint’ high if (YU<XL) or (XU<YL)
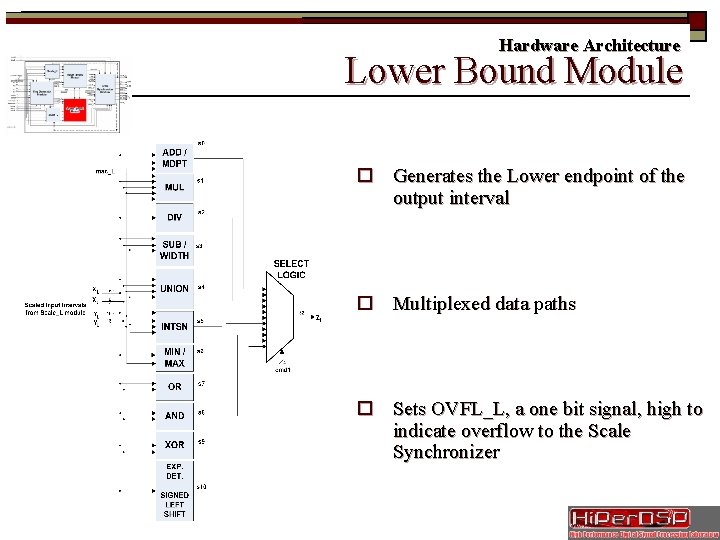
Hardware Architecture Slide 18/35 Lower Bound Module o Generates the Lower endpoint of the output interval o Multiplexed data paths o Sets OVFL_L, a one bit signal, high to indicate overflow to the Scale Synchronizer

Hardware Architecture Slide 19/35 Upper Bound Module o Generates the Upper endpoint of the output interval. o Same structure as Lower Bound module. o Generates 1 -bit signal OVFL_U to indicate overflow in the Upper Bound to the Scale Synchronizer module.

Hardware Architecture BFP Operations Slide 20/35 EXPONENT DETECTION Identify the redundant sign bits by XOR of successive data bits. Obtain the count of the redundant bits using a priority encoder. LEFT SHIFTING The integer output from the Priority Encoder is the value of γ Single cycle Normalize : Select normalized value from shifted versions of the input using γ as the select line

Hardware Architecture Slide 21/35 Scale Synchronizer q Main functions § Rounding 32 -bit outputs of Lower and Upper Bound modules appropriately to 16 -bits § Synchronizing the output endpoints and updating the increment in output block exponents appropriately (updt_L, updt_U) § Storing the minimum exponent detected during Exponent Detection for a block

Hardware Architecture Scale Synchronizer Slide 22/35 q Interval operations n Outward Rounding n Synchronization q q Overflow flags from the Lower and Upper Bound modules Special case rounding for Upper Bound result n Updating Block exponent increment (updt_L and updt_U) q q q Whether overflow occurred or not in either output endpoint Whether special case rounding occurred or not Whether the operations are iterative or not q Point-wise operations n n n Rounding scheme could be Truncation or Rounding to +∞ No synchronization needed Updating Block Exponent increment q q q Whether overflow occurred or not Whether special case rounding occurred or not Whether the operations are iterative or not
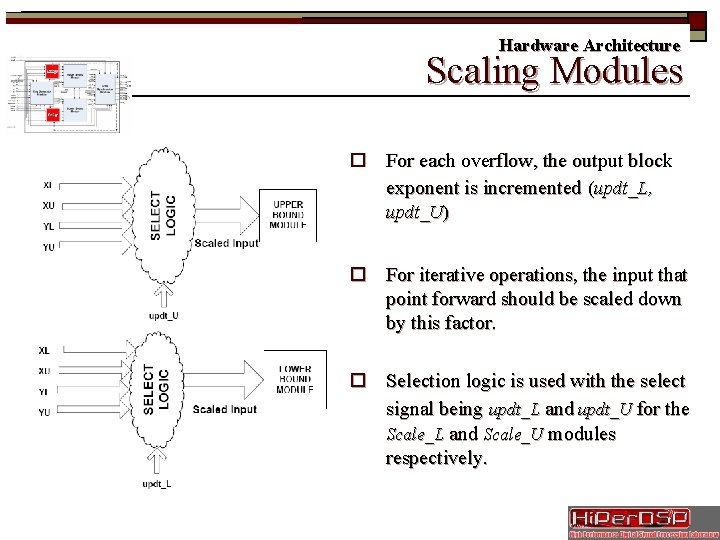
Hardware Architecture Slide 23/35 Scaling Modules o For each overflow, the output block exponent is incremented (updt_L, updt_U) o For iterative operations, the input that point forward should be scaled down by this factor. o Selection logic is used with the select signal being updt_L and updt_U for the Scale_L and Scale_U modules respectively.

Outline q Introduction q Background q Architecture q Results q Conclusions and Future Work q References
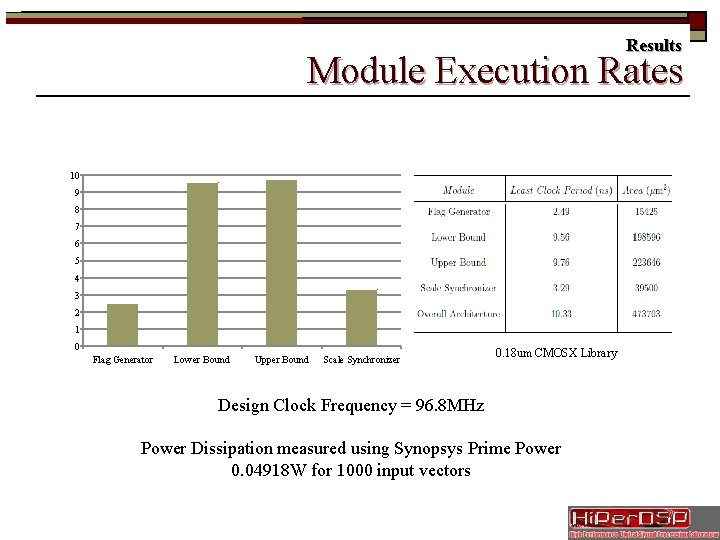
Results Module Execution Rates 10 9 8 7 6 5 4 3 2 1 0 Flag Generator Lower Bound Upper Bound Scale Synchronizer 0. 18 um CMOSX Library Design Clock Frequency = 96. 8 MHz Power Dissipation measured using Synopsys Prime Power 0. 04918 W for 1000 input vectors

Results Evaluating Hardware Performance o Throughput (R) = Number of output samples processed per second o For interval block of size N, (N) cycles needed each for Exponent Detection and Left-shifting to Normalize o 3 cycle penalty per overflow associated with flushing the MAC feedback path, reloading the new block exponent and resuming operations. o Let t =design Timing; p =number of overflows o Probability of nth overflow > Probability of (n-1)th overflow. o In the limiting case of , R = 32. 2 M samples/second

Conclusions and Future Work o Pipeline the Architecture o Adding Saturation for point-wise evaluations o Exploring the BFPIALU as a coprocessor o Developing a Superscalar or VLIW-based interval processor around the ALU

Conclusions and Future Work Conclusion q Developed a competitive hardware solution for reliable interval arithmetic on fixed point architectures q Introduced BFP arithmetic for intervals with CBFS for overflow handling q Enhanced the utility of the architecture by § § expanding the command set. incorporating the ability to perform point-wise arithmetic.

Outline q Introduction q Background q Architecture q Results q Conclusions and Future Work q References
![References [Ruchir 2006] R. Gupte, W. Edmonson, Gianchandani, J, S. Ocloo, and W. Alexander, References [Ruchir 2006] R. Gupte, W. Edmonson, Gianchandani, J, S. Ocloo, and W. Alexander,](http://slidetodoc.com/presentation_image_h2/56f3f1853b6a3d5717855cc7b3e40fd1/image-30.jpg)
References [Ruchir 2006] R. Gupte, W. Edmonson, Gianchandani, J, S. Ocloo, and W. Alexander, “Pipelined ALU for signal processing to implement interval arithmetic, " Signal Processing Systems Design and Implementation IEEE, pp. 95 -100, 2006. [Amaricai 2007] Alexandru Amaricai, Mircea Vladutiu, Lucian Prodan, Mihai Udrescu, Boncalo, Oana, ” Design of Addition and Multiplication Units for High Performance Interval Arithmetic Processor”, Design and Diagnostics of Electronic Circuits and Systems, 2007. DDECS '07. IEEE, April 2007 [Schultz 2000] M. J. Schultz and E. E. Swartzlander, “A family of variable-precision interval arithmetic processors, " IEEE Transactions on Computers, vol. 49, May 2000. [Stine 1998] J. E. Stine and M. J. Schulte, “A combined interval and floating-point multiplier, " 8 th Great Lakes Symposium on VLSI, pp. 208 -213, Feb 1998. [Stine 1998 a] J. E. Stine and M. J. Schulte, “A combined interval and floating-point divider, " IEEE Conference Record on Signals, Systems and Computers, 1998 [Akkas 2002] A. Akkas, “A combined interval and Floating-point comparator/selector, “ Application-Specific Systems, Architectures and Processors, pp. 208 -217, July 2002. [Oppenheim 1970] A. Oppenheim, Realization of digital filters using block-floating-point arithmetic, “ IEEE Transactions on Audio and Electroaccoustics, vol. 18, pp. 130 -136, Jun 1970. [Erickson 1992] A. C. Erickson and B. S. Fagin, Calculating the FHT in hardware, " IEEE Transactions on Signal Processing, vol. 40, June 1992.
![References [Bidet 1995] Bidet E. , Castelain D. , Joanblanq C. and Senn, P. References [Bidet 1995] Bidet E. , Castelain D. , Joanblanq C. and Senn, P.](http://slidetodoc.com/presentation_image_h2/56f3f1853b6a3d5717855cc7b3e40fd1/image-31.jpg)
References [Bidet 1995] Bidet E. , Castelain D. , Joanblanq C. and Senn, P. , ”A fast single-chip implementation of 8192 complex point FFT”, IEEE Journal of Solid-State Circuits, vol. 30, No. 3, pp. 300 -305, Mar 1995 [Van Emden 2001] M. Van Emden, T. Hickey, and Q. Ju, “Interval arithmetic: From principles to implementation, “ Massachusetts Journal of the ACM, vol. 48, pp. 10381068, September 2001. [Liang 2000] Q. Liang and J. M. Mendel, “Overcoming time-varying co-channel interference using Type-2 fuzzy adaptive filters, " IEEE Transactions on Circuits and Systems - II, vol. 47, Dec 2000. [Chhabra 1999] Chhabra and R. Iyer, “A block floating point implementation on the TMS 320 C 54 x DSP, " Tech. Rep. , Texas Instruments, December 1999. Application report SPRA 610. [Kalliojarvi 1996] K. Kalliojarvi and J. Astola, Roundoff errors in block-floating-point systems, " IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 44, pp. 783 -790, April 1996. [Deschamps 2006] J. -P. Deschamps, G. J. A. Bioul, and G. D. Sutter, Synthesis of Arithmetic Circuits. John Wiley & Sons, 2006. [Cragon 1996] H. G. Cragon, Memory Systems and Pipelined Processors. Sudbury, Massachusetts: Jones and Barlett Publishers, 1996. [Hansen 2004] E. Hansen and G. W. Walster, “Global optimization using interval analysis”, Marcel Dekker, Inc. and Sun Microsystems, Inc. , 2004. [intervalhomepage] http: //www. cs. utep. edu/interval-comp/intsoft. html.

Slide 32/35 Thank You !!
- Slides: 32