Bloc de bridage y z O x Une
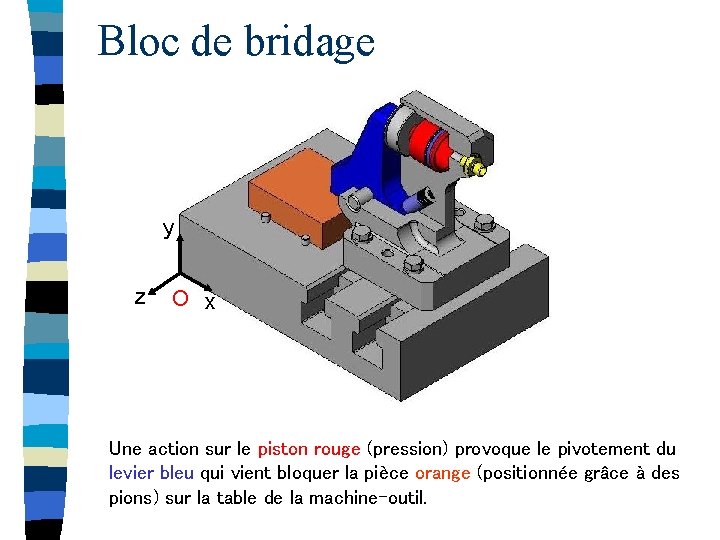
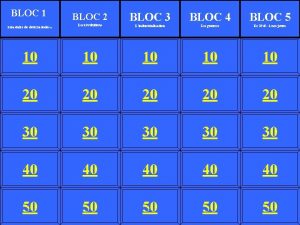
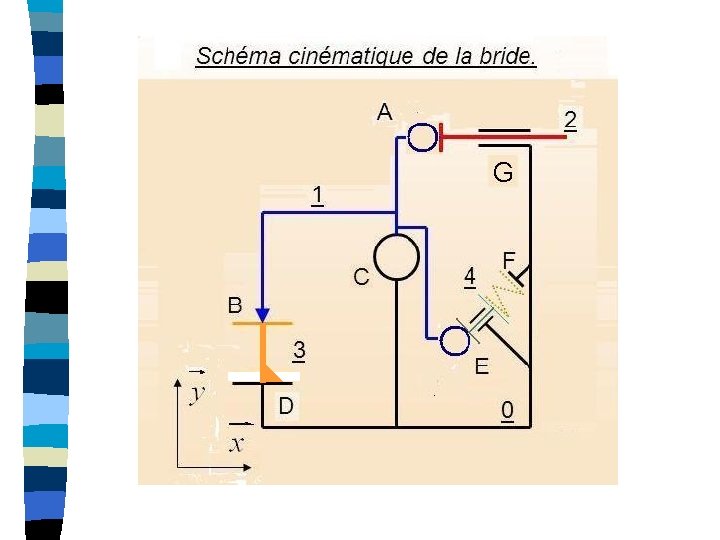
Bloc de bridage y z O x Une action sur le piston rouge (pression) provoque le pivotement du levier bleu qui vient bloquer la pièce orange (positionnée grâce à des pions) sur la table de la machine-outil.
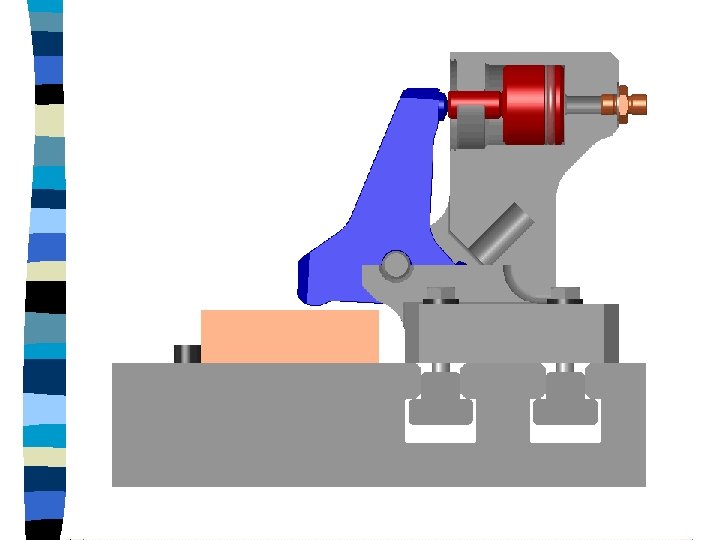
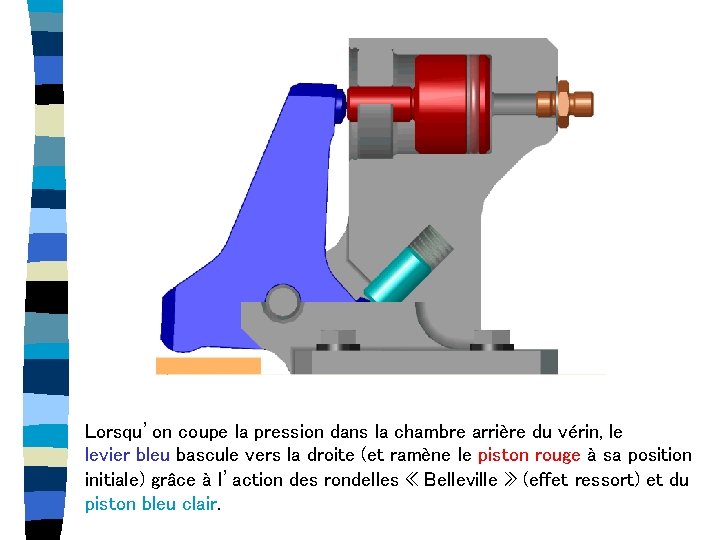
Lorsqu’on coupe la pression dans la chambre arrière du vérin, le levier bleu bascule vers la droite (et ramène le piston rouge à sa position initiale) grâce à l’action des rondelles « Belleville » (effet ressort) et du piston bleu clair.

Modélisation du mécanisme: 1. Etablir les classes d'équivalence du mécanisme. 2. Définir complètement les liaisons entre les solides et tracer le graphe des liaisons. 3. Tracer le schéma cinématique en perspective
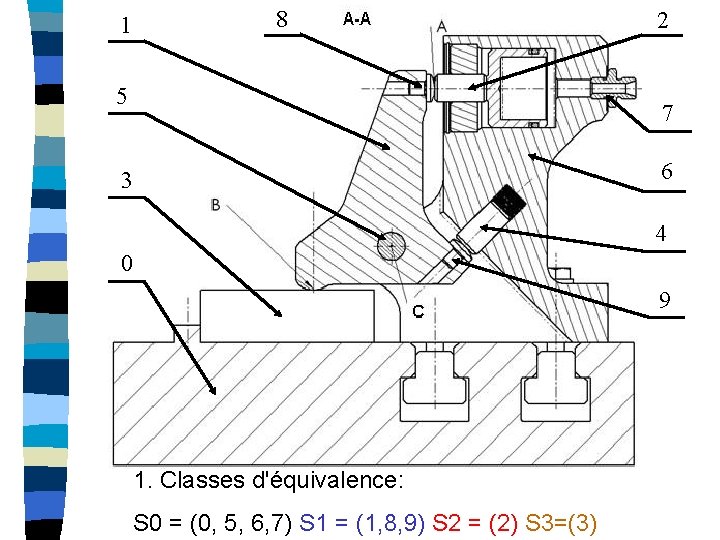
1 8 5 2 7 6 3 4 0 9 1. Classes d'équivalence: S 0 = (0, 5, 6, 7) S 1 = (1, 8, 9) S 2 = (2) S 3=(3)
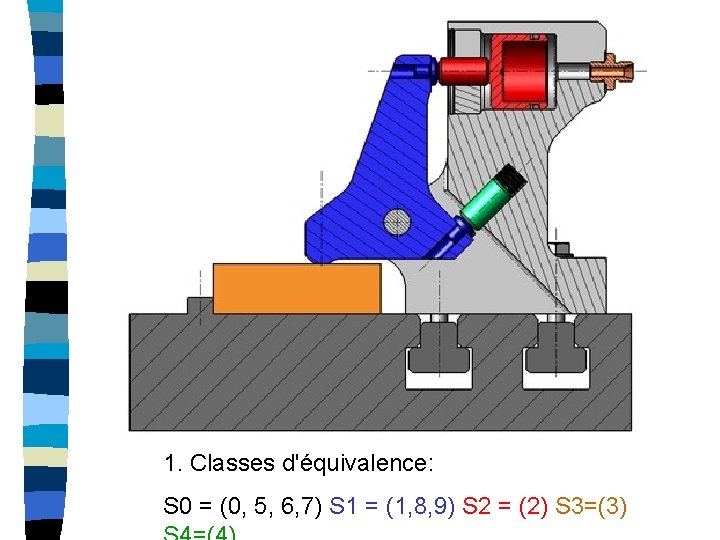
1. Classes d'équivalence: S 0 = (0, 5, 6, 7) S 1 = (1, 8, 9) S 2 = (2) S 3=(3)
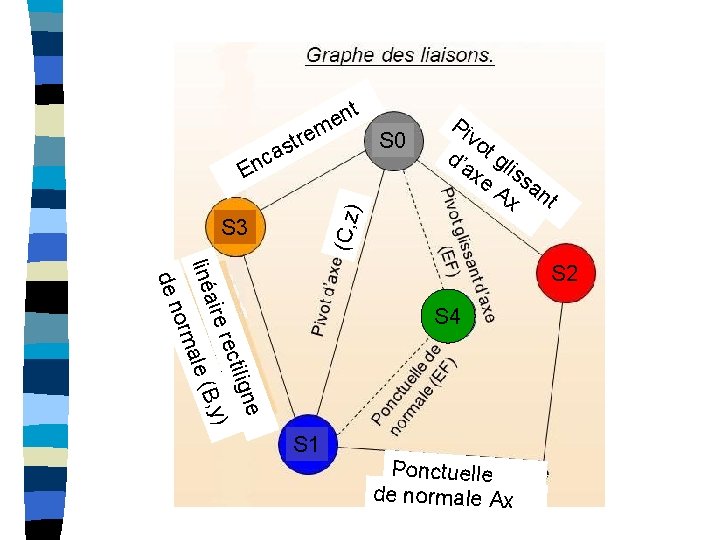
tre as c S 0 Pi vo d’a t gl xe iss Ax ant (C, z ) En nt e m S 3 r aire S 4 4 e lign ecti ) ale orm de n liné S 2 (B, y S 1 Ponctuelle de normale Ax
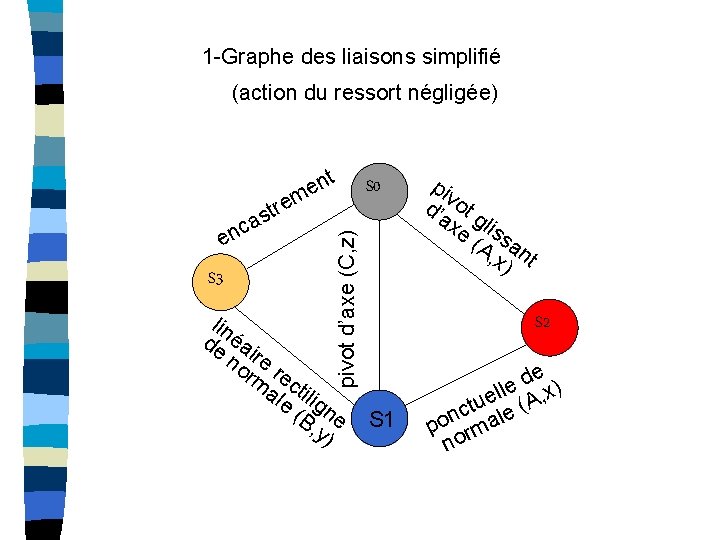
1 -Graphe des liaisons simplifié (action du ressort négligée) S 3 S 0 pivot d’axe (C, z) m e str ca n e t n e lin de éa no ire rm rec ale tili (B gne , y) piv d’a ot g xe lis (A san , x) t S 2 S 1 e d e ll A, x) e ctu le ( n po rma no
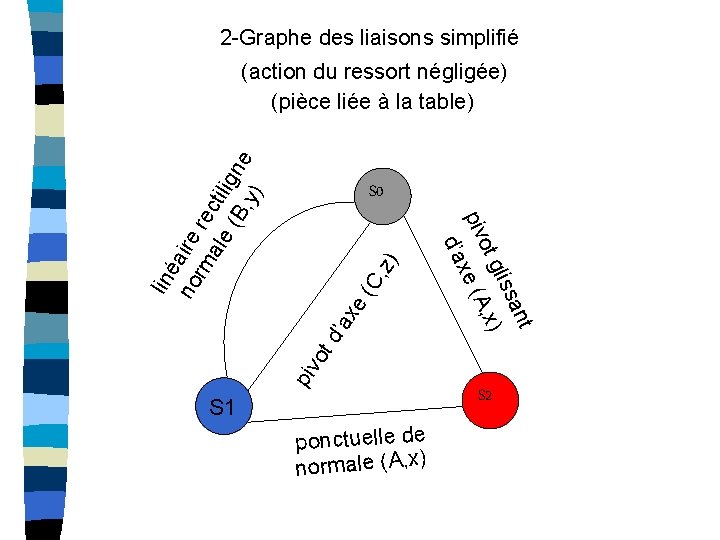
2 -Graphe des liaisons simplifié lin éa no ire rm re ale ctil (B igne , y) (action du ressort négligée) (pièce liée à la table) C, e( ’ax piv o td ant liss , x) ot g piv xe (A d’a z) S 0 S 1 ponctuelle de normale (A, x) S 2
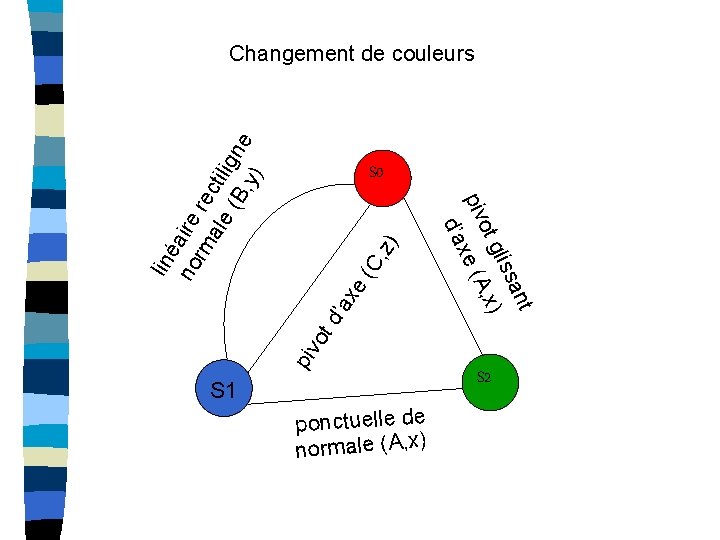
lin éa no ire rm re ale ctil (B igne , y) Changement de couleurs C, e( ’ax piv o td ant liss , x) ot g piv xe (A d’a z) S 0 S 1 ponctuelle de normale (A, x) S 2
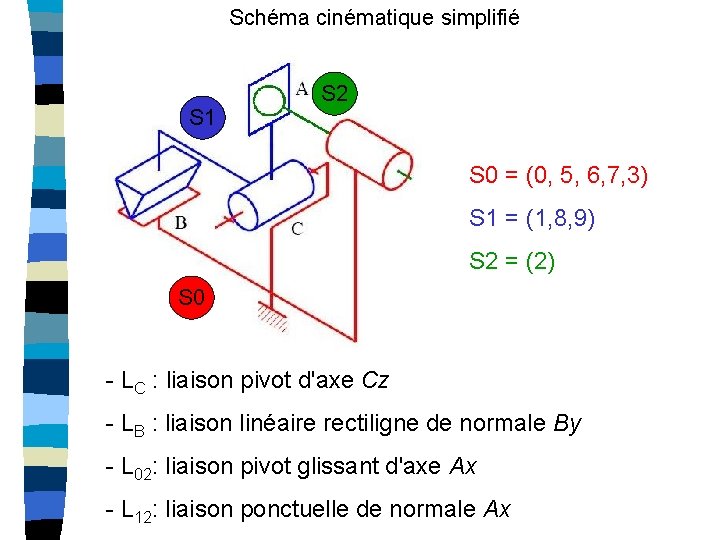
Schéma cinématique simplifié S 1 S 2 S 0 = (0, 5, 6, 7, 3) S 1 = (1, 8, 9) S 2 = (2) S 0 - LC : liaison pivot d'axe Cz - LB : liaison linéaire rectiligne de normale By - L 02: liaison pivot glissant d'axe Ax - L 12: liaison ponctuelle de normale Ax

Etude statique: Hypothèses: – le problème possède un plan de symétrie matériel – le poids des pièces et l'action du ressort sont négligés – les liaisons sont supposées parfaites

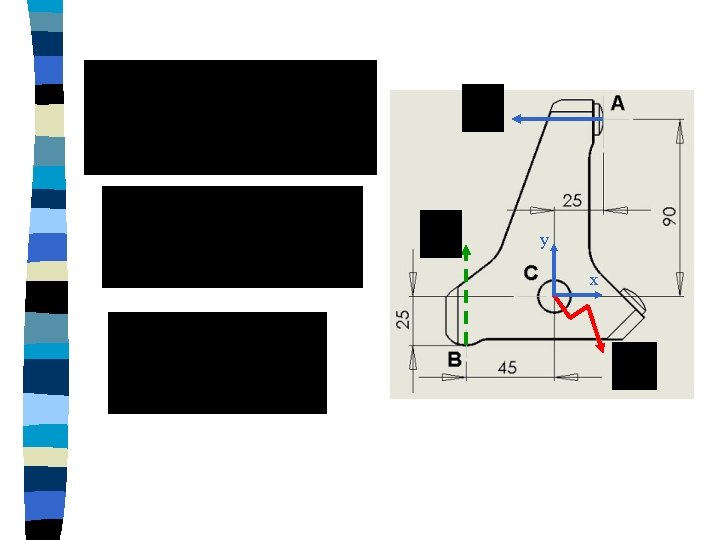
Données: – L'action du piston (2) sur le levier (3) a une intensité de 500 N – Coordonnées des points: C (0, 0, 0); A (6, 44, 0) B (38, -7, 0)
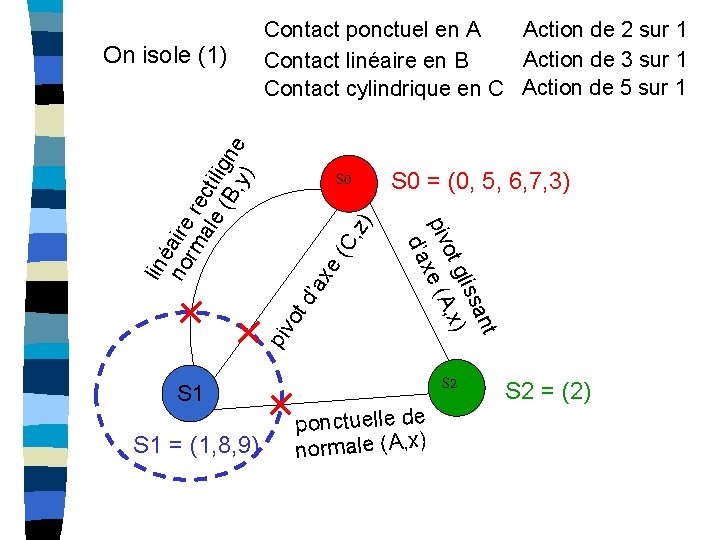
piv o td ’ax e( C, z) S 0 S 1 = (1, 8, 9) S 0 = (0, 5, 6, 7, 3) ant liss ot g , x) piv xe (A d’a lin é no aire rm re ale cti (B ligne , y) On isole (1) Contact ponctuel en A Action de 2 sur 1 Action de 3 sur 1 Contact linéaire en B Contact cylindrique en C Action de 5 sur 1 S 2 ponctuelle de normale (A, x) S 2 = (2)
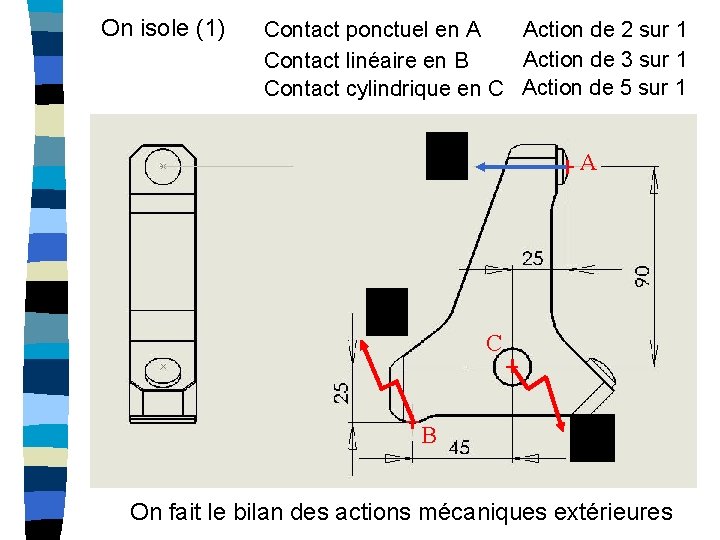
On isole (1) Contact ponctuel en A Action de 2 sur 1 Action de 3 sur 1 Contact linéaire en B Contact cylindrique en C Action de 5 sur 1 A C B On fait le bilan des actions mécaniques extérieures
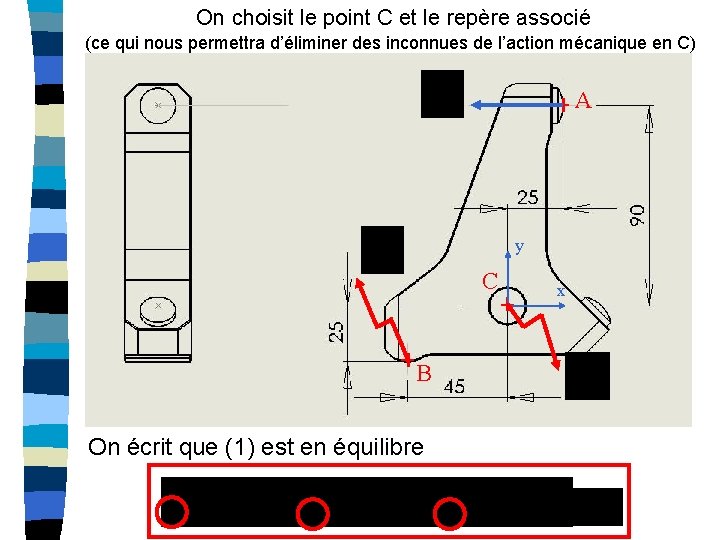
On choisit le point C et le repère associé (ce qui nous permettra d’éliminer des inconnues de l’action mécanique en C) A y C B On écrit que (1) est en équilibre x
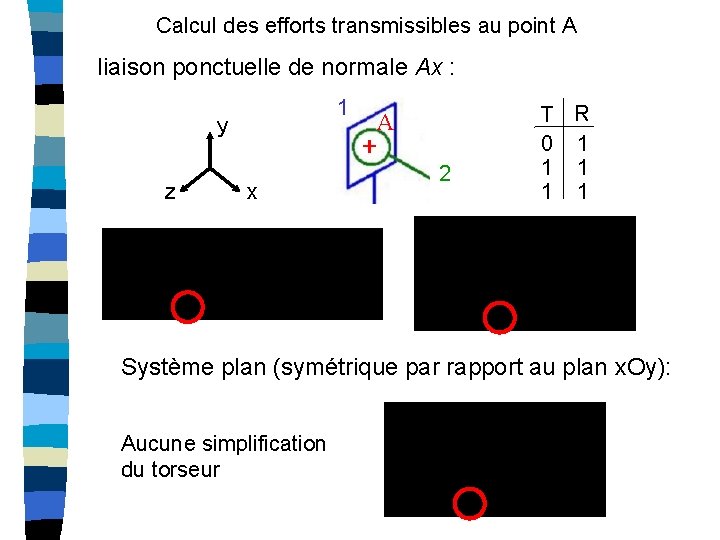
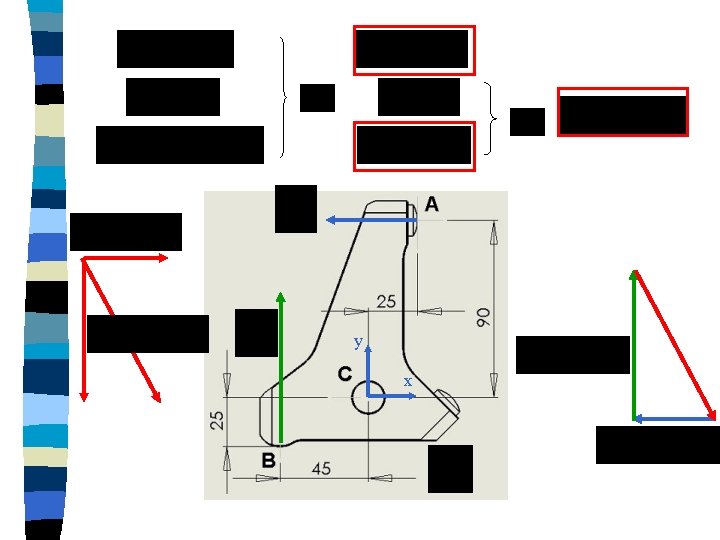
Calcul des efforts transmissibles au point A liaison ponctuelle de normale Ax : 1 y z x A 2 T R 0 1 1 1 Système plan (symétrique par rapport au plan x. Oy): Aucune simplification du torseur
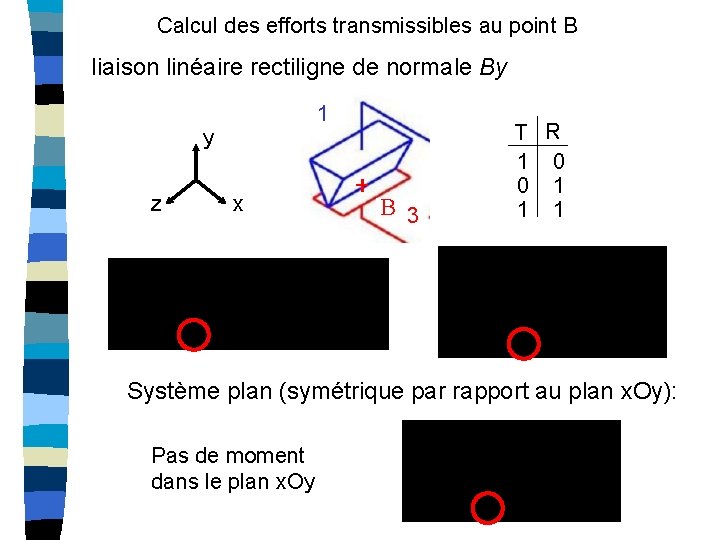
Calcul des efforts transmissibles au point B liaison linéaire rectiligne de normale By 1 y z x B 3 T R 1 0 0 1 1 1 Système plan (symétrique par rapport au plan x. Oy): Pas de moment dans le plan x. Oy
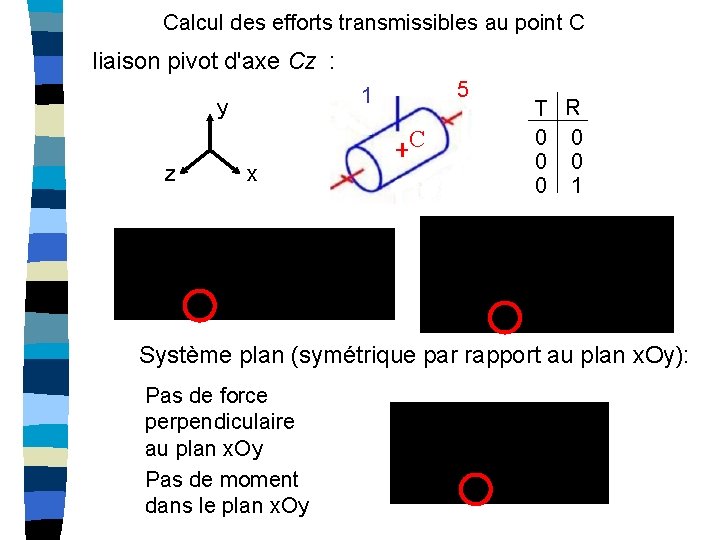
Calcul des efforts transmissibles au point C liaison pivot d'axe Cz : 5 1 y C z x T R 0 0 0 1 Système plan (symétrique par rapport au plan x. Oy): Pas de force perpendiculaire au plan x. Oy Pas de moment dans le plan x. Oy

La somme des actions mécaniques aux points A, B et C est égale à O ATTENTION tous les torseurs doivent être exprimés au même point et dans le même repère On choisit le point C et le repère associé
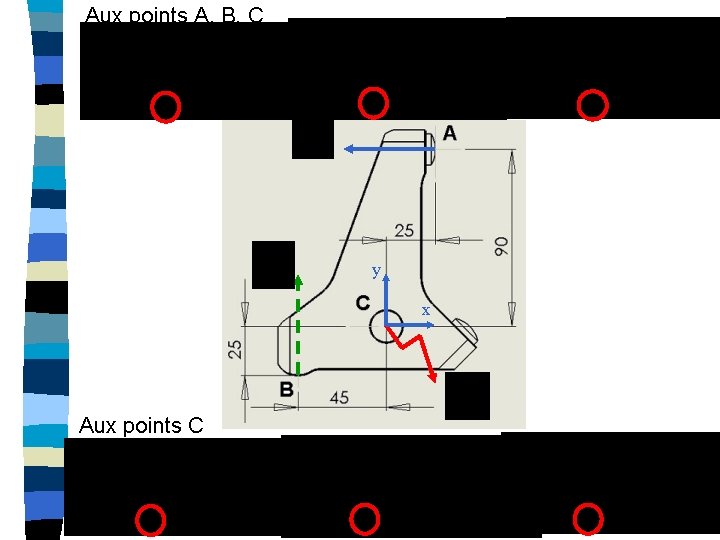
Aux points A, B, C y x Aux points C
y x
y x
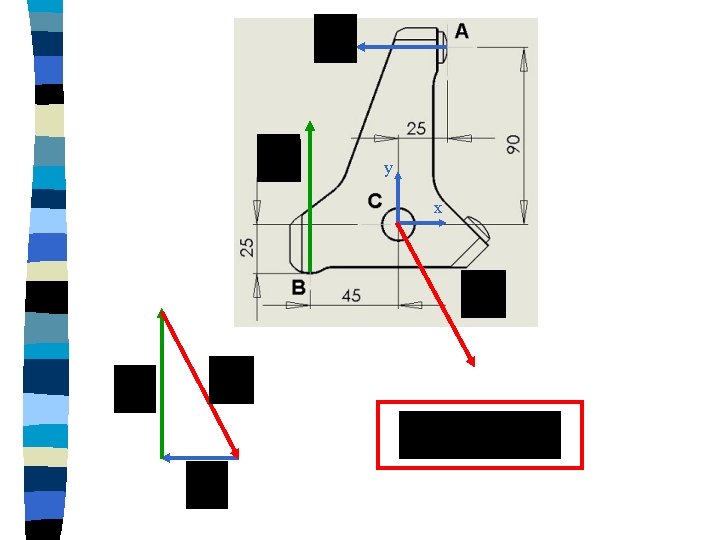
y x
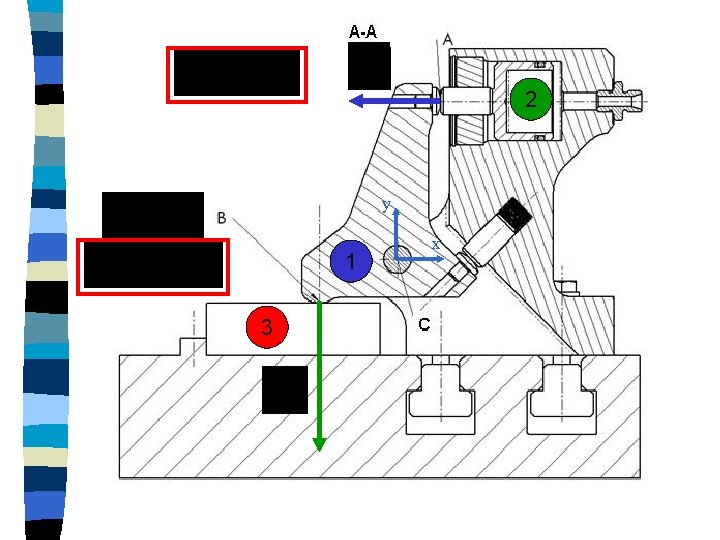
2 y 1 3 x
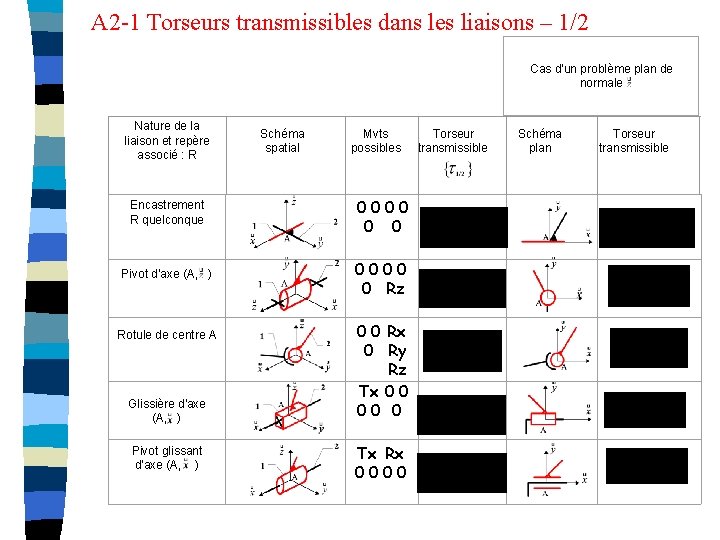
A 2 -1 Torseurs transmissibles dans les liaisons – 1/2 Cas d'un problème plan de normale Nature de la liaison et repère associé : R Schéma spatial Mvts possibles Encastrement R quelconque 0000 0 0 Pivot d'axe (A, ) 0000 0 Rz Rotule de centre A Glissière d'axe (A, ) Pivot glissant d'axe (A, ) 0 0 Rx 0 Ry Rz Tx 0 0 00 0 Tx Rx 0000 Torseur transmissible Schéma plan Torseur transmissible
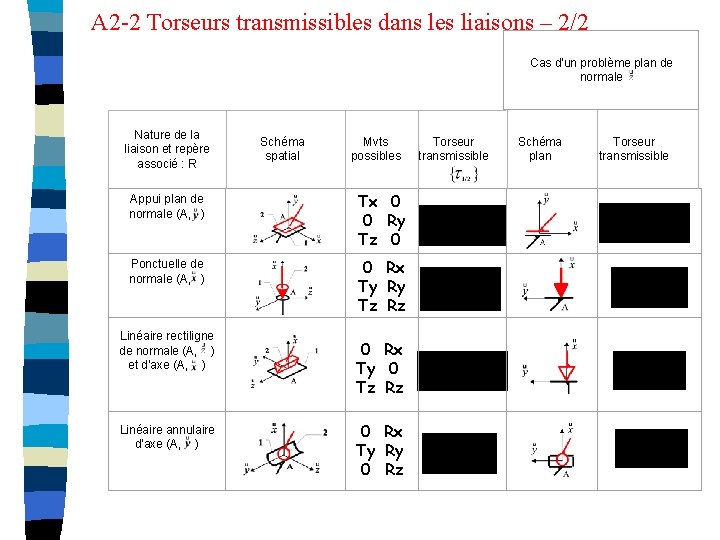
A 2 -2 Torseurs transmissibles dans les liaisons – 2/2 Cas d'un problème plan de normale Nature de la liaison et repère associé : R Schéma spatial Mvts possibles Appui plan de normale (A, ) Tx 0 0 Ry Tz 0 Ponctuelle de normale (A, ) 0 Rx Ty Ry Tz Rz Linéaire rectiligne de normale (A, ) et d’axe (A, ) Linéaire annulaire d'axe (A, ) 0 Rx Ty 0 Tz Rz 0 Rx Ty Ry 0 Rz Torseur transmissible Schéma plan Torseur transmissible
- Slides: 28