Blm 11 Asal Momentum Asal Momentum Asal momentum

Bölüm 11 Açısal Momentum

Açısal Momentum Açısal momentum dönme hareketinde önemli rol oynar. Açısal momentumun korunumunun prensipleri vardır. Lineer momentumun korunumunun prensiplerine benzerdir. Yalıtılmış bir sistemin açısal momentum sabittir. Açısal momentum için, yalıtılmış sistem dış torkun sistem üzerine etki etmediği bir sistemdir. Açısal momentumun korunum yasası fiziğin temel kurallarındandır. Relativistik ve kuantum sistemler için de geçerlidir. Giriş

Vektörel Çarpım İki vektörün vektörel çarpımının başka bir vektör olduğu örnekler vardır. İki vektörün çarpımının skaler olduğunu daha önceden görmüştük. Buna nokta çarpım da denir. İki vektörün vektörel çarpıma çapraz çarpım da denir. Kesim 11. 1
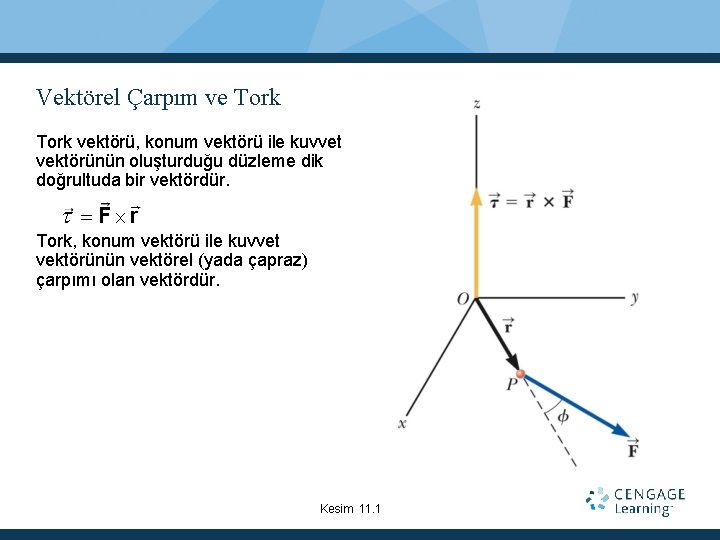
Vektörel Çarpım ve Tork vektörü, konum vektörü ile kuvvet vektörünün oluşturduğu düzleme dik doğrultuda bir vektördür. F r Tork, konum vektörü ile kuvvet vektörünün vektörel (yada çapraz) çarpımı olan vektördür. Kesim 11. 1

Vektörel Çarpım A and B gibi iki vektör veriliyor A ve B nin vektörel (çapraz) çarpımı üçüncü vektör, C A B gibidir. C, “A çapraz çarpımı B” gibi okunur. C vektörünün büyüklüğü AB sin dir. ise the angle between A ile B nin arasındaki açıdır. Section 11. 1
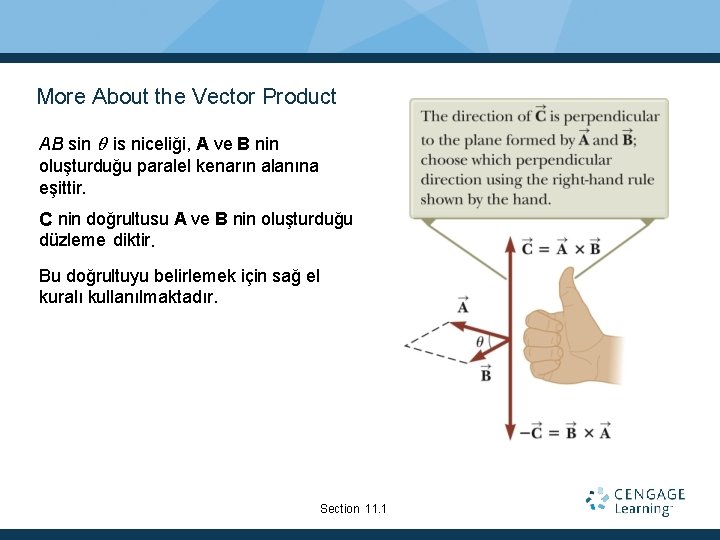
More About the Vector Product AB sin is niceliği, A ve B nin oluşturduğu paralel kenarın alanına eşittir. C nin doğrultusu A ve B nin oluşturduğu düzleme diktir. Bu doğrultuyu belirlemek için sağ el kuralı kullanılmaktadır. Section 11. 1

Vektörel Çarpımın Özellikleri Vektörel çarpımda yerdeğiştirme özelliği yoktur. Vektörel çarpımın mertebesi önemlidir. Ax. B=-Bx. A olduğunu hatırlayınız, A, B ye paralel ise ( = 0 o or 180 o), o halde A B 0 Buna göre A A 0 A, B ye dikse, o zaman A B AB Vektörel çarpım dağılma kuralına uyar. A x (B + C) = A x B + A x C Section 11. 1

Vektörel Çarpımın Son Özelliği Vektörel çarpımın zamana göre türevi d d. A d. B A B B A dt dt dt dir vektörün çarpımının mertebesini korumak önemlidir. Section 11. 1

Birim vektörlerin vektörel çarpımı i i j j k k 0 i j j i k j k k j i k i i k j Section 11. 1

Vektörel Çarpımın İşareti İşaretler çapraz çarpımda karşılıklı yerdeğiştirebilir. A -B A B veˆi ˆj ˆi ˆj Section 11. 1

Determinant kullanımı Çapraz çarpım i j k A B Ax Ay A Bx By Bz z Ay By Az Ax i� Bz Bx Az A j x Bx Bz Ay By ? k gibi ifade edilebilir. determinantı açarsak gives A B Ay Bz Az By i � Ax Bz Az Bx j Ax By Ay Bx k Section 11. 1

Vektörel Çarpıma Örnek A=2 i+3 j; B=-i+2 j veriliyor A B yi bulunuz Sonuç A B (2 i+3 j) -i+2 j) 2 i ( i) 2 i 2 j+3 j (-i)+ 3 j 2 j 0 4 k+3 k+0=7 k Section 11. 1

Tork ile Vektörel Çarpım Örneği Kuvvet ve yer veriliyor F=(2, 00 i+3, 00 j) N r (4, 00 i+5. 00 j) m Oluşan torku bulunuz r F [(2, 00 i+3, 00 j) N] [(4, 00 i+5. 00 j) m] 2, 00 i 4, 00 i+ 2, 00 i 5. 00 j+3, 00 j 4, 00 i+3, 00 j 5. 00 j 0+10 k-12 k+0=-2 k N m Section 11. 1

Açısal Momentum r konumuna yerleştirilmiş ve p doğrusal momentumla hareket eden m kütleli bir parçacığı dikkate alalım. Net torku bulunuz. dt r F r dp dr p terimi ilave ediniz. dt d(r dt p) Kuvvetin öteleme hareketinde ve torkun dönme hareketinde aynı rolü oynamasından dolayı doğrusal momentumu cinsinden net kuvvet için bu denkleme çok benzer gözükür. Section 11. 2
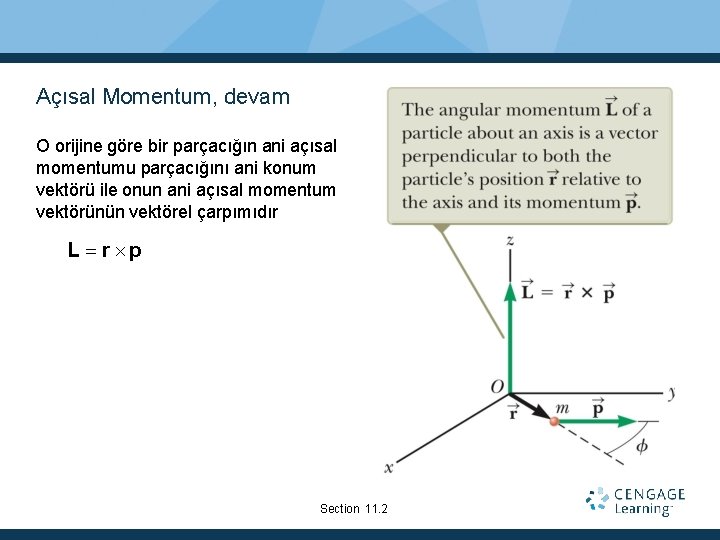
Açısal Momentum, devam O orijine göre bir parçacığın ani açısal momentumu parçacığını ani konum vektörü ile onun ani açısal momentum vektörünün vektörel çarpımıdır L r p Section 11. 2

Tork ve Açısal Momentum Tork açısal momentuma bağlıdır. Kuvvet te aynı şekilde doğrusal momentuma bağlıdır. d. L dt Bir parçacığa etki eden tork parçacığın açısal momentumun zamana göre değişimine eşittir. Bu Newton’un İkinci Yasasının dönme hareketinin karşılığıdır. ve L aynı orijin civarında ölçülmelidir. Bu eylemsiz koordinat sisteminde sabitlenmiş orijin için geçerlidir. Section 11. 2

Açısal momentum hakkında daha fazla bilgi Açısal momentumun SI birimi (kg. m 2)/ s dir. Açısal momentumun hem büyüklüğü hem de doğrultusu orijin seçimine bağlıdır. Açısal momentumun büyüklüğü L = mvr sin dir. , r ve p arasındaki açıdır. L nin yönü r ve p oluşturduğu düzleme diktir. Section 11. 2
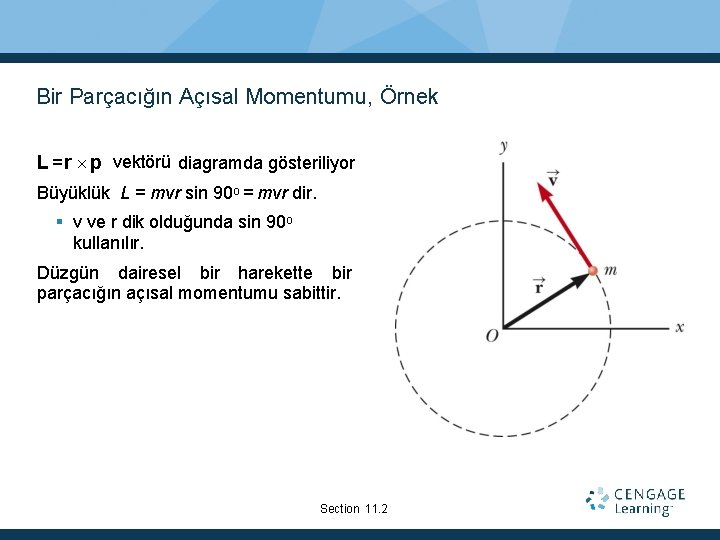
Bir Parçacığın Açısal Momentumu, Örnek L =r p vektörü diagramda gösteriliyor Büyüklük L = mvr sin 90 o = mvr dir. v ve r dik olduğunda sin 90 o kullanılır. Düzgün dairesel bir harekette bir parçacığın açısal momentumu sabittir. Section 11. 2

Parçacık Sisteminin Açısal Momentumu Parçacık sisteminin toplam açısal momentumu bireysel parçacıkların açısal momentumlarının vektörel toplamıdır. L tot L 1 L 2 Ln Li Zaman göre türevini alırsak d. L tot d. Li i dt dt i i i Section 11. 2

Parçacık Sisteminin Açısal Momentumu devamı Parçacık sistemine etki eden dış kuvvetlere eşlik eden herhangi bir tork sıfırdır. Buna göre, ext tot d. L dt Eylemsiz koordinat sisteminde orijinden geçen bazı eksen etrafında bir sistem üzerine etki eden net dış tork orijin etrafında sistemin toplam açısal momentumun zamana göre değişimine eşittir. Bu yalıtımsız sistem modelin açısal momentum versiyonun matematiksel temsilidir. Denklemi tekrar düzenlersek, dt L ext Bu açısal itme-açısal momentum teoremidir. Section 11. 2 tot verir.

Parçacık Sisteminin Açısal Momentumu, sonu Kütle merkezi boyunca bir eksen etrafında bir sisteme etki eden bileşke tork kütle merkezi hareketin bakmaksızın sistemin açısal momentumun zaman göre değişimine eşittir. Bu kütle merkezi ivmelense bile uygulanır ve sağlanan ve L kütle merkezine göre değerlendirilir. Section 11. 2
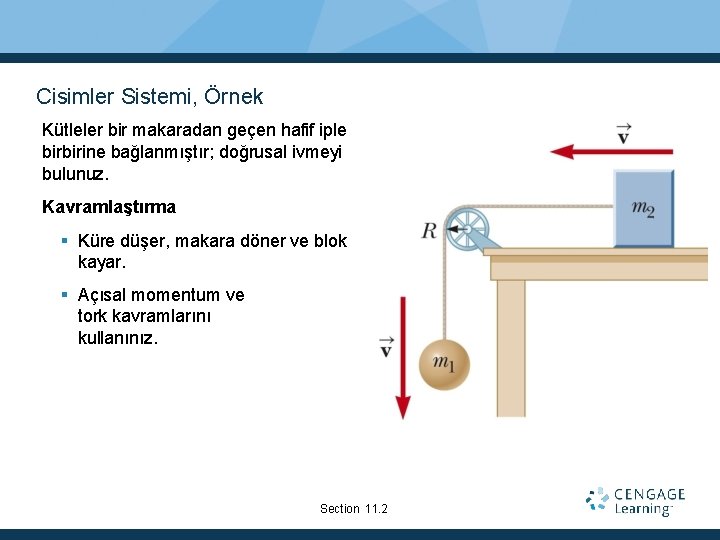
Cisimler Sistemi, Örnek Kütleler bir makaradan geçen hafif iple birbirine bağlanmıştır; doğrusal ivmeyi bulunuz. Kavramlaştırma Küre düşer, makara döner ve blok kayar. Açısal momentum ve tork kavramlarını kullanınız. Section 11. 2

Cisimler Sistemi, Örnek devam. Sınıflandırınız Blok, makara ve küre yalıtımsız bir sistemdir. Küre üzerine etki eden yerçekimi kuvvetinden dolayı dış torka maruz kalır. Makaranın eksine karşılık gelen ekseni kullanınız. Sistemin açısal momentumu iki cismin ötelemeli hareketini içine alır ve saf dönmeye maruz kalır. Analiz ediniz Zamanın herhangi bir anında, küre ve blok yaygın v hızına sahip olur. Açısal momentum ve net dış tork ifadelerini yazınız. İfadeyi doğrusal ivme için çözünüz. Section 11. 2

Cisimler sistemi, Örnek son Son haline getiriniz Tüm olarak sistemi analiz ediniz ve iç kuvvetleri ihmal edebilirsiniz. Sadece dış kuvvetler gereklidir. Sadece dış kuvvetler sistemin açısal momentumunu değiştirmek için katkıda bulunur. Section 11. 2
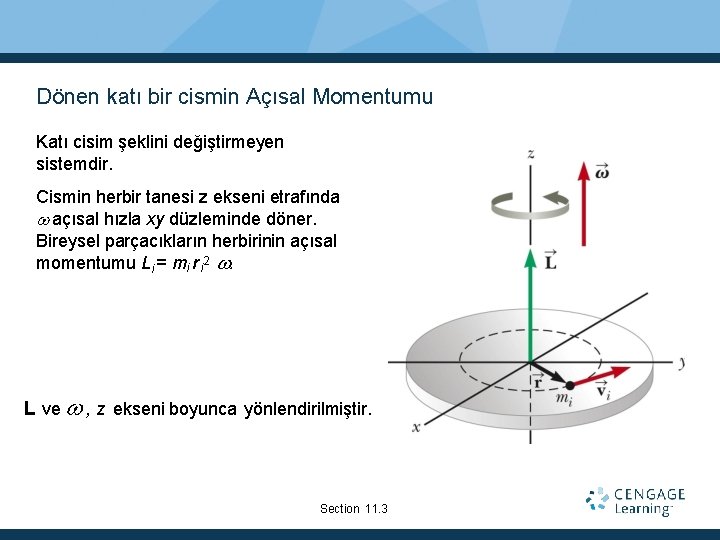
Dönen katı bir cismin Açısal Momentumu Katı cisim şeklini değiştirmeyen sistemdir. Cismin herbir tanesi z ekseni etrafında açısal hızla xy düzleminde döner. Bireysel parçacıkların herbirinin açısal momentumu Li = mi r i 2 L ve , z ekseni boyunca yönlendirilmiştir. Section 11. 3

Dönen Katı bir Cismin Açısal Momentumu, devam Tüm cismin açısal momentumunu bulmak için, tüm bireysel parçacıkların açısal momentumlarını ilave ediniz. Lz Li mi ri 2 I i i Türevini alırsak, bu bize Newton Yasasının dönme hareketi formunu verir. d. Lz d I I ext dt dt Bu, katı cismin net tork analiz modelin altındaki matematiksel temsilidir. Section 11. 3

Dönen Katı bir Cismin Açısal Momentumu, son Newton’un İkinci Yasasının dönme hareketi formu hatta dönme ekseninin sağladığı dönme ekseni etrafında dönmesi geçerlidir: (1) kütle merkezinden geçmesi (2) simetri ekseni olması Simetrik cisimler, kütle merkezinden geçen sabit eksen etrafında dönerse, vektör formu: L I dir L , dönme eksenine göre ölçülen toplam açısal momentumdur. L, dönme ekseni boyunca açısal momentumun bileşenine karşılık gelirse, Newton’un ikinci yasasının dönme hareketi formu simetri ne olursa olsun herhangi bir cisim için geçerlidir. Section 11. 3
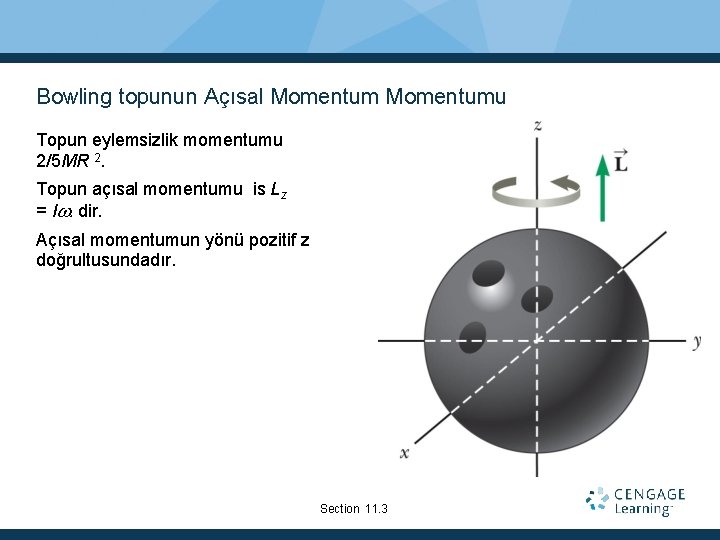
Bowling topunun Açısal Momentumu Topun eylemsizlik momentumu 2/5 MR 2. Topun açısal momentumu is Lz = I dir. Açısal momentumun yönü pozitif z doğrultusundadır. Section 11. 3

Açısal Momentumun Korunumu Sisteme etki eden net dış tork sıfır ise, sistemin toplam açısal momentumun hem yönü hem de büyüklüğü sabittir. Sistemin yalıtık olması tet torkun = 0 olması anlamına gelir. Bu yalıtılmış sistem modelin açısal momentum versiyonun temelidir. L top = sabit yada Li = Ls Parçacıklar sistemi için L top = L n = sabit Section 11. 4

Açısal Momentumun Korunumu, devamı Yalıtılmış sistemin kütlesinin tekrar dağılıma maruz kaldığı durumda sistem şeklini değiştirirse, eylemsizlik momenti değişir. Açısal momentumun korunumu açısal hızı tanzim eden değişimi içerir. Ii i = If f = sabit Bu, sabit eksen etrafındaki dönme ve hareket eden sistemin kütle merkezi boyunca eksen etrafında dönme olur. Herhangi bir durumda net tork sıfır olmalıdır. Section 11. 4

Korunum Yasası Özet Yalıtılmış bir Sistem için- (1) Enerjinin Korunumu: Ei = Es Sistem sınırları boyunca enerji transferi yoksa (2) Doğrusal Momentumun Korunumu: p i ps Sistem üzerine başka kuvvet yoksa sıfır (3) Açısal Momentumun Korunumu: L i Ls Sistem üzerine başka dış kuvvet yoksa sıfırdır Section 11. 4

Korunum Yasaları– Notlar Bir sistem diğer niceliklerin cinsinden değil bu niceliklerin birisine göre yalıtılmış olabilir. Örneğin, bir sistem çoğu kez momentum cinsinden yalıtılmış değil hatta enerji cinsinde de yalıtılmış değildir fakat net kuvvet yada tork onun üzerine etki eder. Sistem enerji cinsinden yalıtılmış olmayabilir ama momentum cinsinde yalıtılmış olabilir. Çarpışmalar çoğu kez momentum cinsinden yalıtılmış fakat enerji cinsinden yalıtılmamıştır. Section 11. 4
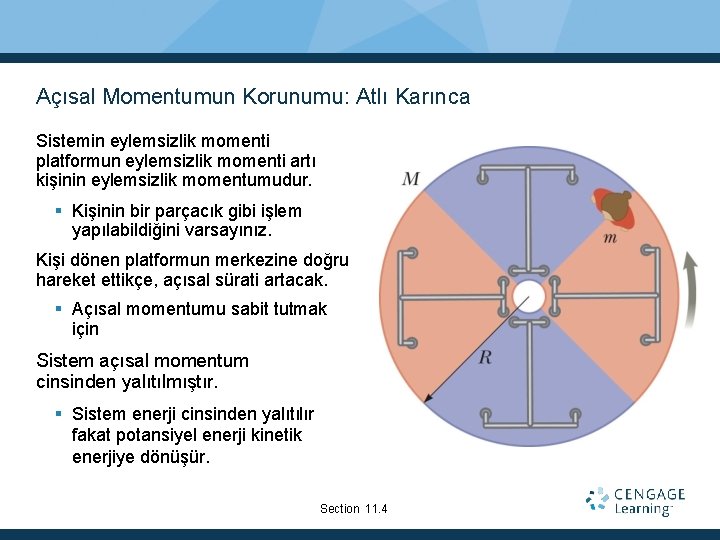
Açısal Momentumun Korunumu: Atlı Karınca Sistemin eylemsizlik momenti platformun eylemsizlik momenti artı kişinin eylemsizlik momentumudur. Kişinin bir parçacık gibi işlem yapılabildiğini varsayınız. Kişi dönen platformun merkezine doğru hareket ettikçe, açısal sürati artacak. Açısal momentumu sabit tutmak için Sistem açısal momentum cinsinden yalıtılmıştır. Sistem enerji cinsinden yalıtılır fakat potansiyel enerji kinetik enerjiye dönüşür. Section 11. 4
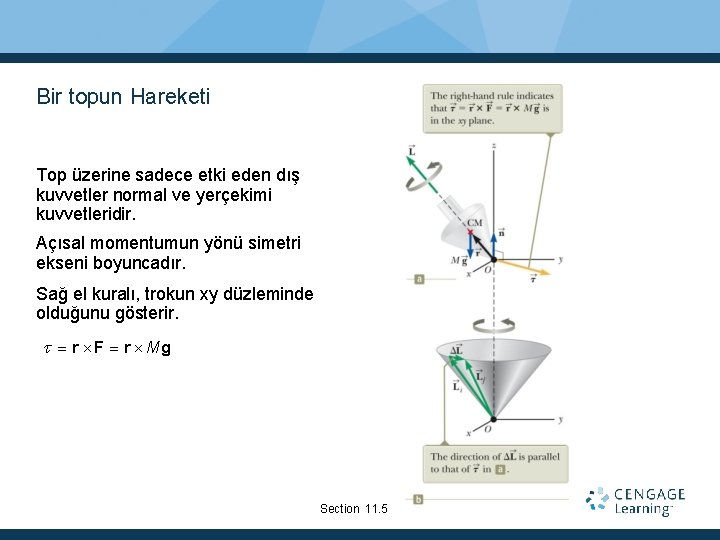
Bir topun Hareketi Top üzerine sadece etki eden dış kuvvetler normal ve yerçekimi kuvvetleridir. Açısal momentumun yönü simetri ekseni boyuncadır. Sağ el kuralı, trokun xy düzleminde olduğunu gösterir. r F r Mg Section 11. 5

Bir Topun Hareketi, devam Net tork and açısal momentum birbirine bağlıdır: ext d. L dt Açısal momentumun değişimi sıfırdan farklı bir oluşturur. Açısal momentumun değişimin sonucu z ekseni etrafında topaç hareketini doğurur. Açısal momentumun doğrultusu değişiyor. Topaç hareketi düşey etrafında simetri eksenin hareketidir. Topaç hareketi ekseriye topun dönme hareketine göre yavaştır. Section 11. 5

Jiroskop topaç hareketin göstermek için kullanılabilir. Yerçekimi kuvveti pivot etrafında tork üretir ve bu tork eksene diktir. Normal kuvvet tok üretmez. Section 11. 5

Jiroskop, devam Eksene dik momentumdaki sonuçlanır. doğrultuda açısal bir değişim torkla Eksen dt zaman aralığında d açısıyla tarar. Açısal momentumun büyüklüğü değil doğrultusu değişiyor. Jiroskop, topaç hareketi yapar.

Jiroskop, Son Bunu basitleştirmek için, pivot etrafında kütle merkezi hareketinden dolayı açısal momentumun sıfır olduğunu varsayınız. Buna göre, toplam açısal momentum onun dönmesinden dolayıdır. çok büyük olduğu zaman, bu iyi bir yaklaşımdır. Section 11. 5

Topaç hareketi frekansı Şekil 11. 14 c deki vektörü analiz edersek, eksenin düşey eksen etrafında döndüğü hız bulunabilir. d Mgr. KM p dt I p topaç hareketi frekansıdır Bu sadece p << olduğu zaman geçerlidir. Section 11. 5
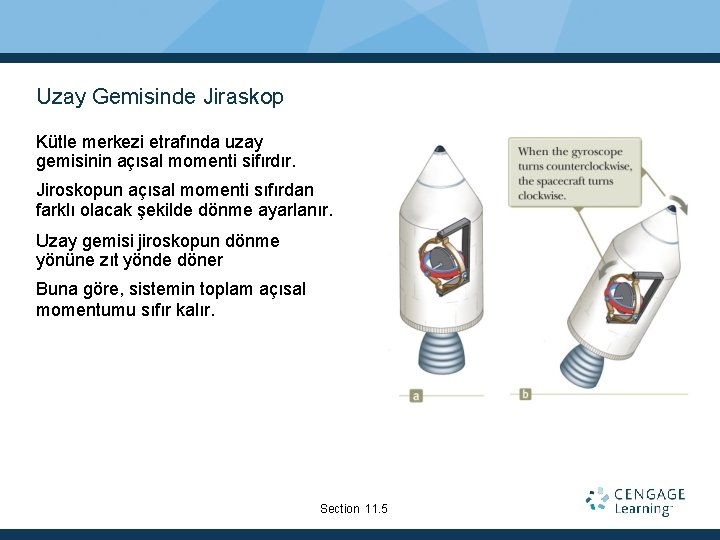
Uzay Gemisinde Jiraskop Kütle merkezi etrafında uzay gemisinin açısal momenti sifırdır. Jiroskopun açısal momenti sıfırdan farklı olacak şekilde dönme ayarlanır. Uzay gemisi jiroskopun dönme yönüne zıt yönde döner Buna göre, sistemin toplam açısal momentumu sıfır kalır. Section 11. 5

Yeni Analiz Modeli – Yalıtılmamış Sistem (Açısal Momentum) Bir sistem, sistem üzerinde dış torkun var olduğu çevreyle karşılıklı etkileşirse, sistem üzerine etki eden net dış tork onun açısal momentumun zamana göre değişimine eşittir. d. Ltot ext dt Summary
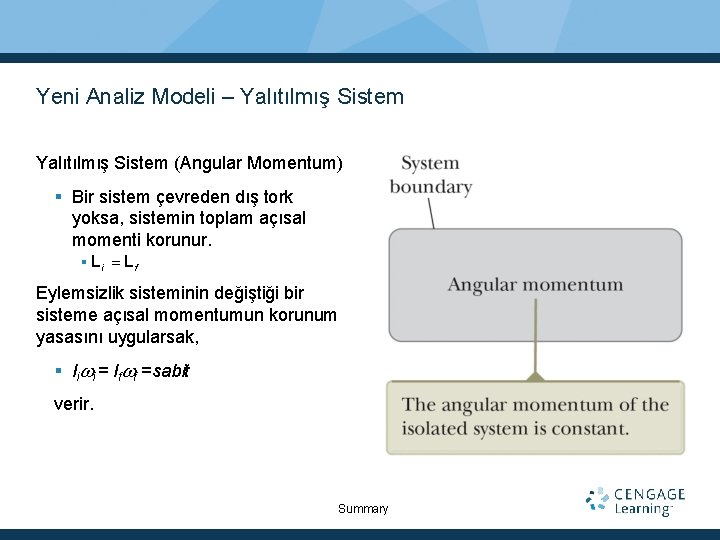
Yeni Analiz Modeli – Yalıtılmış Sistem (Angular Momentum) Bir sistem çevreden dış tork yoksa, sistemin toplam açısal momenti korunur. Li Lf Eylemsizlik sisteminin değiştiği bir sisteme açısal momentumun korunum yasasını uygularsak, Ii i = If f = sabit verir. Summary
- Slides: 42