Blind Inverse Gamma Correction Hany Farid IEEE Trans

Blind Inverse Gamma Correction (Hany Farid , IEEE Trans. Signal Processing, vol. 10 no. 10, October 2001) An article review Merav Kass January 2003

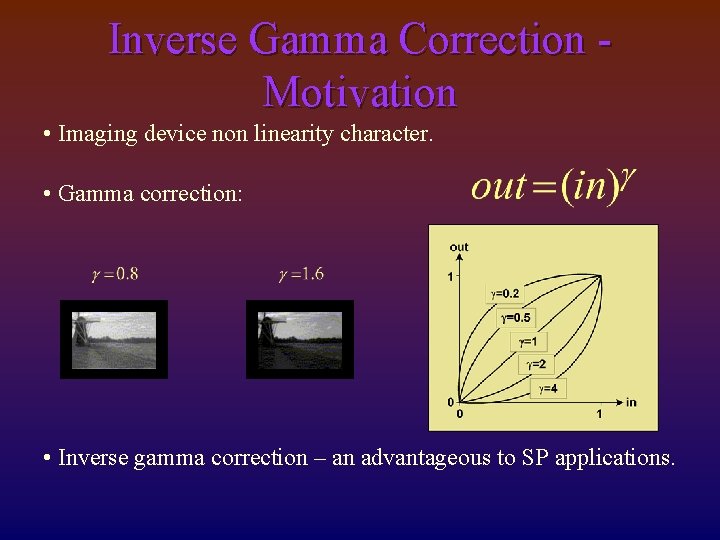
Inverse Gamma Correction Motivation • Imaging device non linearity character. • Gamma correction: • Inverse gamma correction – an advantageous to SP applications.

Blind Inverse Gamma Correction Motivation • If g is known: • Typically, g is determined experimentally. The imaging device calibration information The need in blind inverse gamma correction arise!

What? & How? What is a blind inverse Gamma correction ? • It is an estimation process. • No prior knowledge is assumed. How does it work ? • Minimize higher-order correlation in the frequency domain.

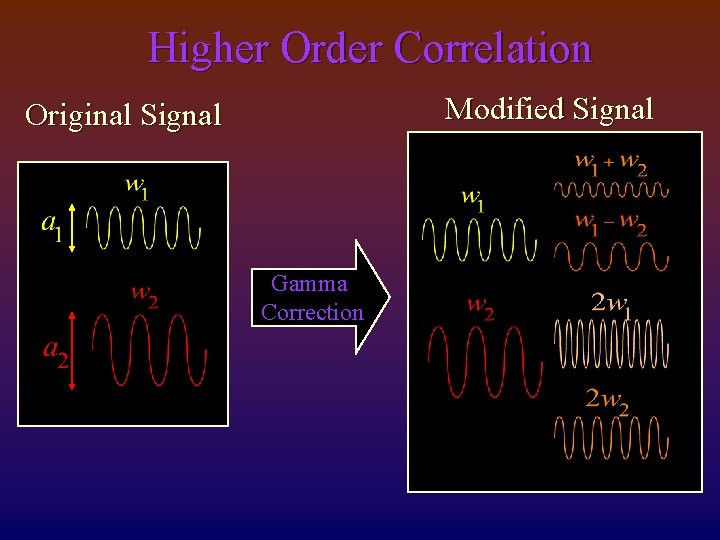
Higher Order Correlation Modified Signal Original Signal Gamma Correction

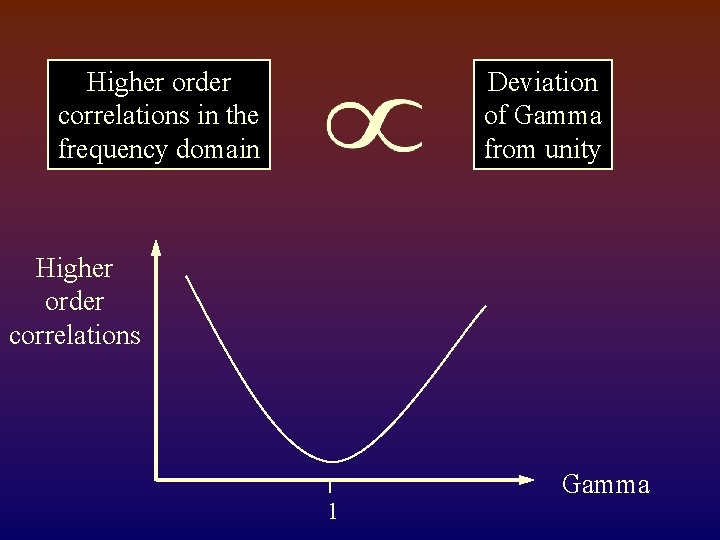
Higher order correlations in the frequency domain Deviation of Gamma from unity Higher order correlations 1 Gamma

How higher order correlations can be measured ? By estimating the bicoherence function: It reveals the sort of higher order correlations introduced by nonlinearity.

The Algorithm Assumptions • Only one parameter has to be estimated : gamma. • The only thing we have to work with is the a gamma corrected image.

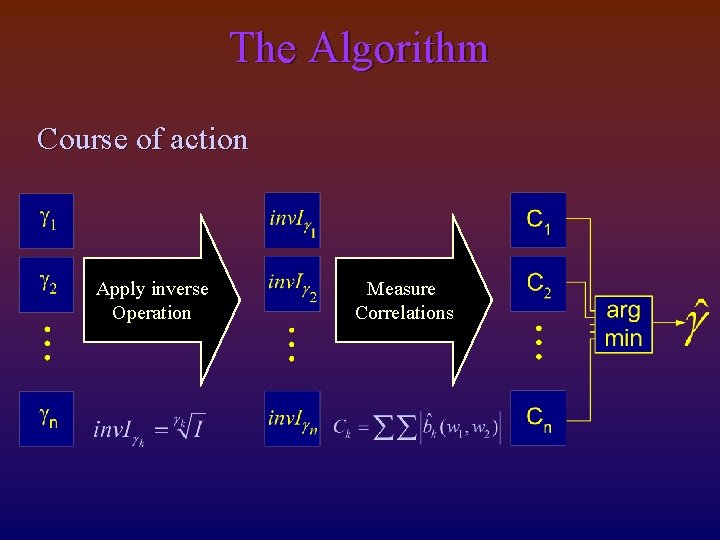
The Algorithm Course of action Apply inverse Operation Measure Correlations

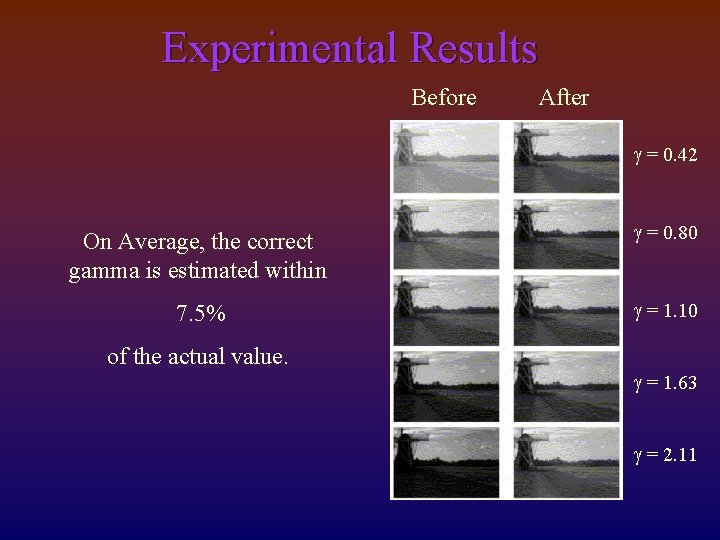
Experimental Results Before After g = 0. 42 On Average, the correct gamma is estimated within g = 0. 80 7. 5% g = 1. 10 of the actual value. g = 1. 63 g = 2. 11

Additional Notes • C(g) is a well behaved function. • Calculation efficiency. • The algorithm performance in presence of additive noise. • The algorithm performance in presence of linear transformations. • Colored images.

Restrictions and Limitations • One parameter model is assumed. • The procedure assume to be uniform.