BLACK HOLES and WORMHOLES PRODUCTION AT THE LHC

BLACK HOLES and WORMHOLES PRODUCTION AT THE LHC I. Ya. Aref’eva Steklov Mathematical Institute, Moscow

BLACK HOLES and WORMHOLES PRODUCTION AT THE LHC • I-st lecture. • BLACK HOLES. • 2 -nd lecture. • • BH formation Trapped surfaces • 3 -rd lecture. • • • WORMHOLES TIME MACHINES WHY on LHC? Cross-sections and signatures of BH/WH production at the LHC BH in GR and in QG BH/WH production in Trans-Planckian Collisions I. Aref’eva BH/WH at LHC, Dubna, Sept. 2008

I-st lecture. Outlook: • BLACK HOLES in GR • Historical Remarks • SCHWARZSCHILD BH • Event Horizon • Trapped Surfaces • BH Formation Refs. : L. D. Landau, E. M. Lifshitz, The Classical Theory of Fields, II v. Hawking S. , Ellis J. The large scale structure of space-time. R. Wald, General Relativity, 1984 S. Carroll, Spacetime and Geometry. An introduction to general relativity, 2004 • BLACK HOLES in QG • BLACK HOLES in Semi-classical approximation to QG I. Aref’eva BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Historical Remarks • The Schwarzschild solution has been found in 1916. The Schwarzschild solution(SS) is a solution of the vacuum Einstein equations, which is spherically symmetric and depends on a positive parameter M, the mass. In the coordinate system in which it was originally discovered, (t, r, theta, phi), had a singularity at r=2 M • In 1923 Birkoff proved a theorem that the Schwarzschild solution is the only spherically symmetric solution of the vacuum E. Eqs. • In 1924 Eddington, made a coordinate change which transformed the Schwarzschild metric into a form which is not singular at r=2 M • In 1933 Lemaitre realized that the singularity at r=2 M is not a true singularity • In 1958 Finkelstein rediscovered Eddington's transformation and realized that the hypersurface r=2 M is an event horizon, the boundary of the region of spacetime which is causally connected to infinity. I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Historical Remarks • In 1950 Synge constructed a systems of coordinates that covers the complete analytic extension of the SS • In 1960 Kruskal and Szekeres (independently) discovered a single most convenient system that covers the complete analytic extension of SS • In 1964 Penrose introduced the concept of null infinity, which made possible the precise general definition of a future event horizon as the boundary of the causal past of future null infinity. • In 1965 Penrose introduced the concept of a closed trapped surface and proved the first singularity theorem (incompleteness theorem). • Hawking-Penrose theorem: a spacetime with a complete future null infnity which contains a closed trapped surface must contain a future event horizon (H-E-books, 9 -2 -1) I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Schwarzschild solution to vacuum Einstein eq. A general metric in a spherically symmetric spacetime (Ch. 13 of Weinberg) Christoffel symbols, Riemann tensor, Ricci tensor 1) 2) 1) 4) I. Aref’eva 3) 2) 5) I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Schwarzschild solution to vacuum Einstein eq. A general metric in a spherically symmetric spacetime (Ch. 13 of Weinberg) Christoffel symbols, Riemann tensor, Ricci tensor I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Schwarzschild solution • Asymptoticaly flat • Birkhoff's theorem: Schwarzschild solution is the unique spherically symmetric vacuum solution • Singularity I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

D-dimensional Schwarzschild Solution Meyers, … I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BLACK HOLES in GR. Schwarzschild solution • Geodesics Null Geodesics I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008
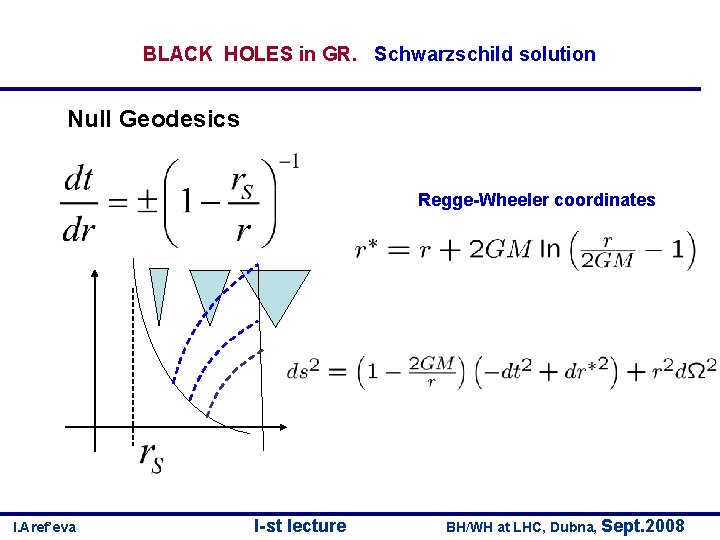
BLACK HOLES in GR. Schwarzschild solution Null Geodesics Regge-Wheeler coordinates I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008
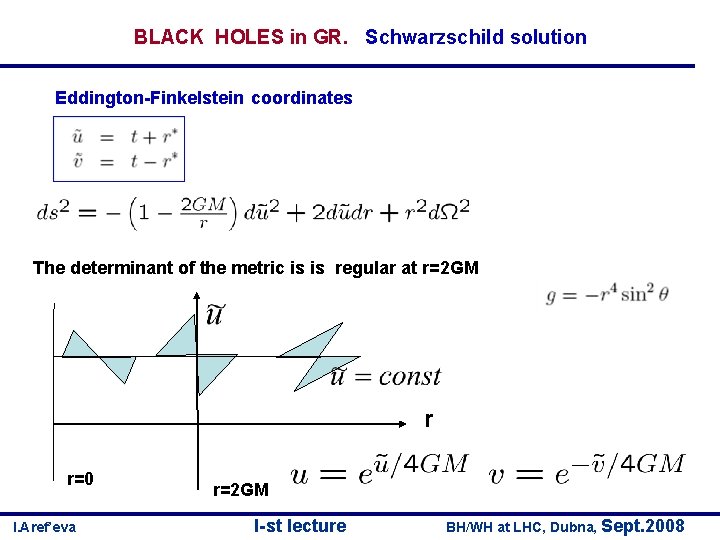
BLACK HOLES in GR. Schwarzschild solution Eddington-Finkelstein coordinates The determinant of the metric is is regular at r=2 GM r r=0 I. Aref’eva r=2 GM I-st lecture BH/WH at LHC, Dubna, Sept. 2008
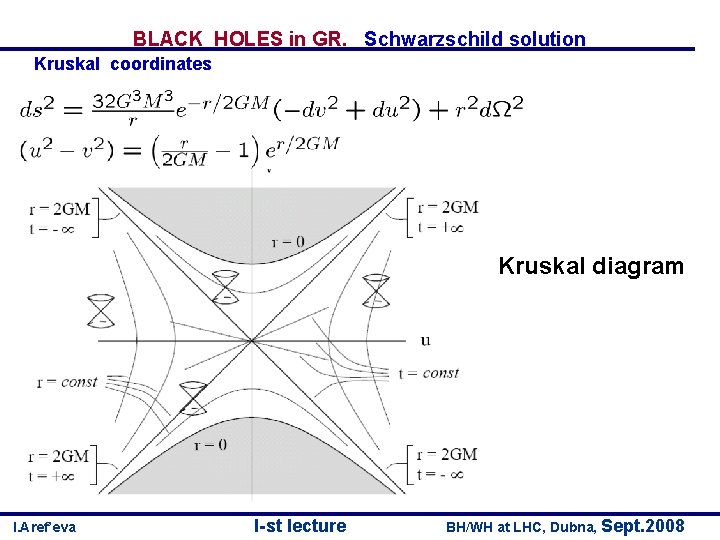
BLACK HOLES in GR. Schwarzschild solution Kruskal coordinates Kruskal diagram I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008
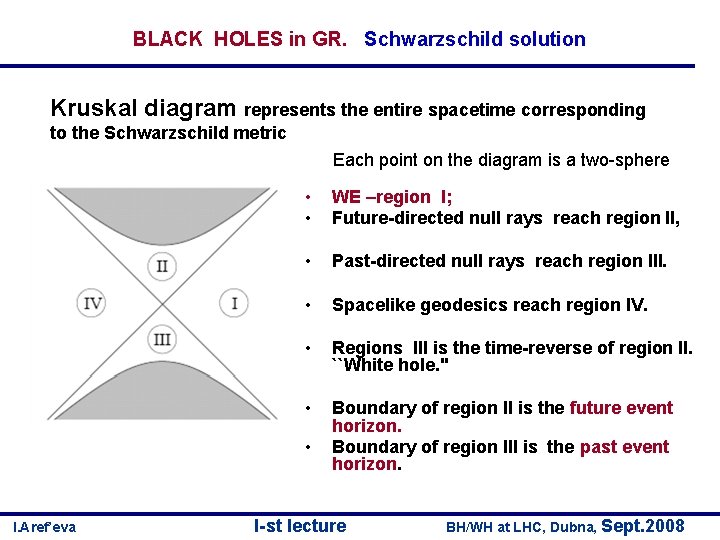
BLACK HOLES in GR. Schwarzschild solution Kruskal diagram represents the entire spacetime corresponding to the Schwarzschild metric Each point on the diagram is a two-sphere • • WE –region I; Future-directed null rays reach region II, • Past-directed null rays reach region III. • Spacelike geodesics reach region IV. • Regions III is the time-reverse of region II. ``White hole. '' • Boundary of region II is the future event horizon. Boundary of region III is the past event horizon. • I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008
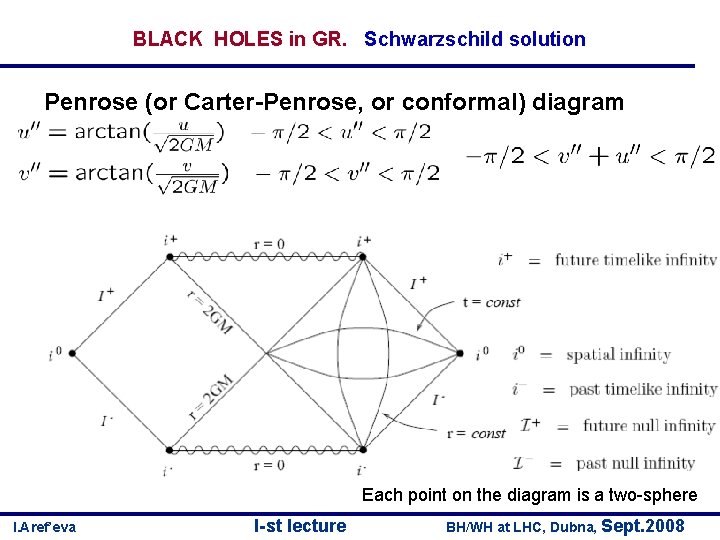
BLACK HOLES in GR. Schwarzschild solution Penrose (or Carter-Penrose, or conformal) diagram Each point on the diagram is a two-sphere I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008
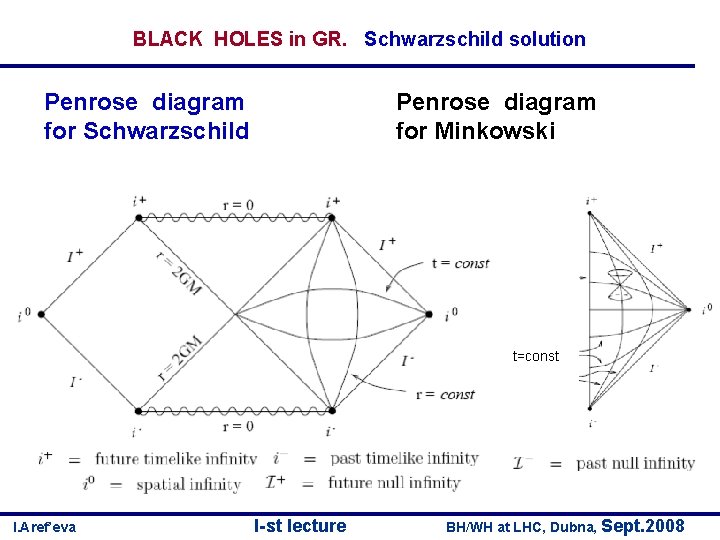
BLACK HOLES in GR. Schwarzschild solution Penrose diagram for Schwarzschild Penrose diagram for Minkowski t=const I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

Event Horizons The event horizon is always a null hypersurface. The event horizon does not depend on a choice of foliation. The event horizon always evolves continuously. The event horizon captures the intuitive idea of the boundary of what can reach observers at infinity. I. Aref’eva I-st lecture BH/WH at LHC, Dubna, Sept. 2008

BH production in QFT Question • Q - can QFT (in flat space-time) produce BH Answer: • A Q - QFT(in flat space-time) cannot produce BH/WH, etc. We can see nonperturbatively just precursor (предвестник) of BHs QFT + "SQG" (semicl. aprox. to QG) can I. Aref’eva BH-QCD, CERN, Sept. 2008

BH in Quantum Gravity Background formalism in QFT I. Aref’eva I-st lecture IA, L. D. Faddeev, A. A. Slavnov, 1975 BH/WH at LHC, Dubna, Sept. 2008

AQ. Analogy with Solitons How to see these solitons in QFT? • perturbative S-matrix for phi-particles - no indications of solitons • Exact nonperturbative S-matrix for phi-particles – extra poles - indications of a soliton-antisoliton state IA, V. Korepin, 1974 I. Aref’eva BH-QCD, CERN, Sept. 2008
- Slides: 20