Black Hole spacetime 1 Local Inertial frame Free

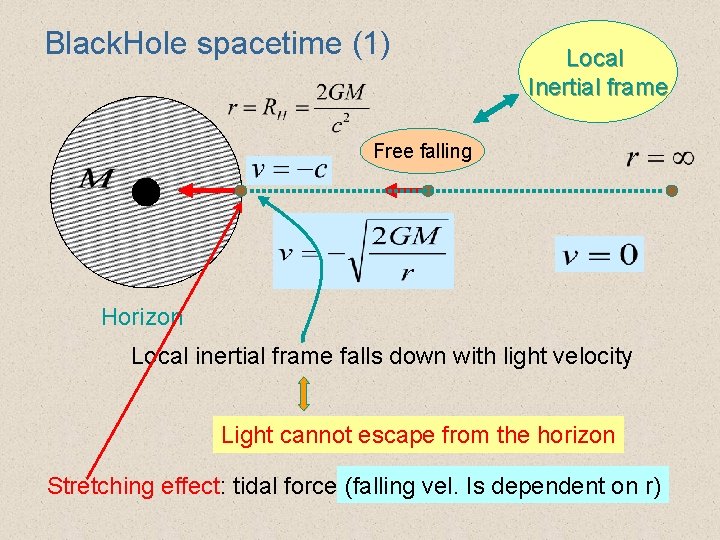
Black. Hole spacetime (1) Local Inertial frame Free falling Horizon Local inertial frame falls down with light velocity Light cannot escape from the horizon Stretching effect: tidal force (falling vel. Is dependent on r)

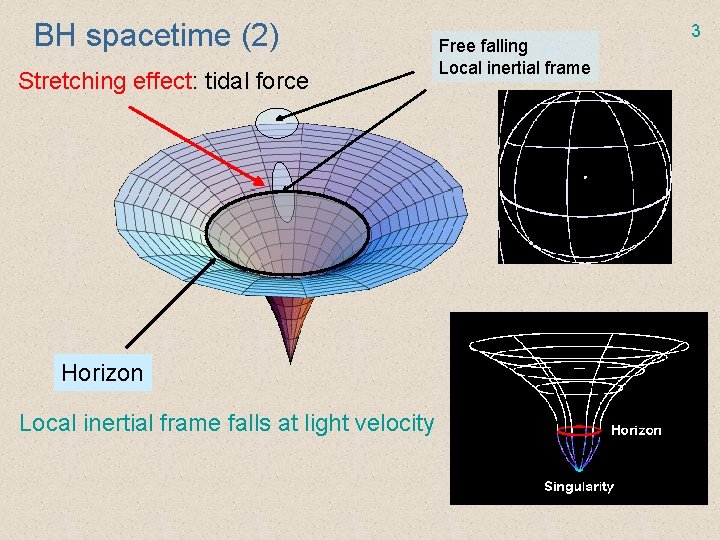
BH spacetime (2) Stretching effect: tidal force Horizon Local inertial frame falls at light velocity Free falling Local inertial frame 3

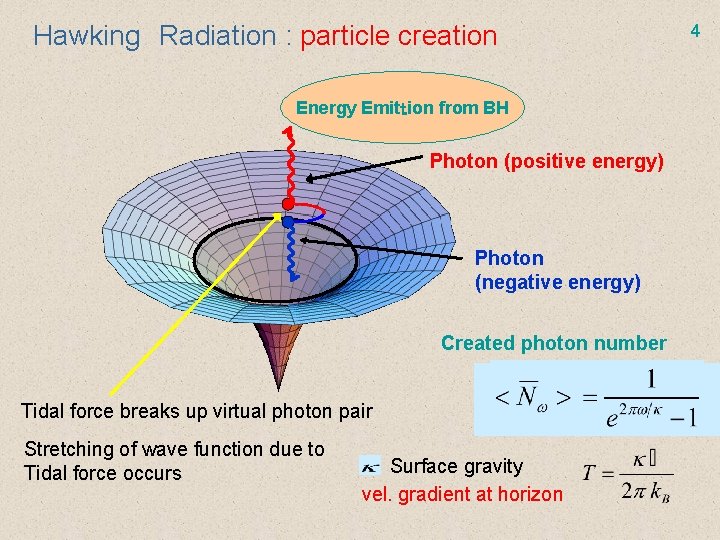
Hawking　Radiation : particle creation Energy Emitｔion from BH Photon (positive energy) Photon (negative energy) Created photon number Tidal force breaks up virtual photon pair Stretching of wave function due to Tidal force occurs Surface gravity vel. gradient at horizon 4

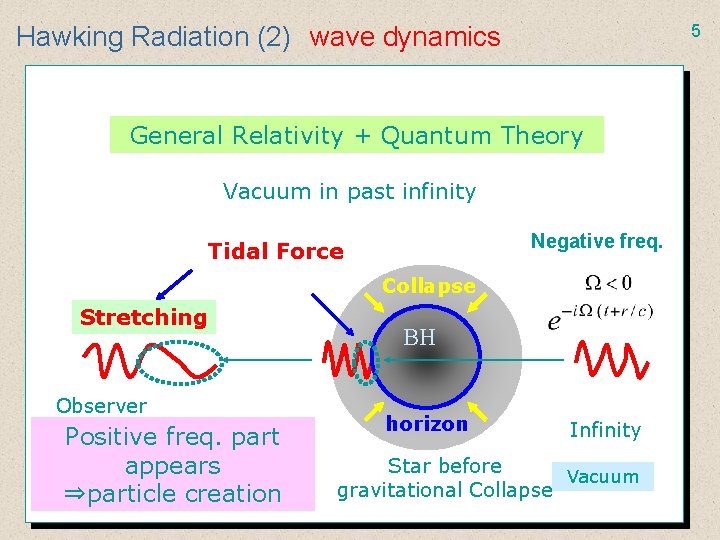
5 Hawking Radiation (2)　wave dynamics General Relativity + Quantum Theory Vacuum in past infinity Negative freq. Tidal Force Collapse Stretching Observer Positive freq. part appears ⇒particle creation BH horizon Infinity Star before Vacuum gravitational Collapse

Acoustic Black Hole Correspondence between BH and its sonic analogue Black Hole spacetime flow with sonic point 　　　light 　　　sound wave Horizon plays essential role in Hawking radiation Observation of HR is quite difficult Sonic Horizon We can easily realize acoustic black hole In laboratories. In case of BEC

7 Sound Waves in Perfect Fluid adiabatic Euler eq. continuity irrotational wave equation for perturbed part of velocity potential This simulates wave propagation in curved spacetime: e. g. black hole.

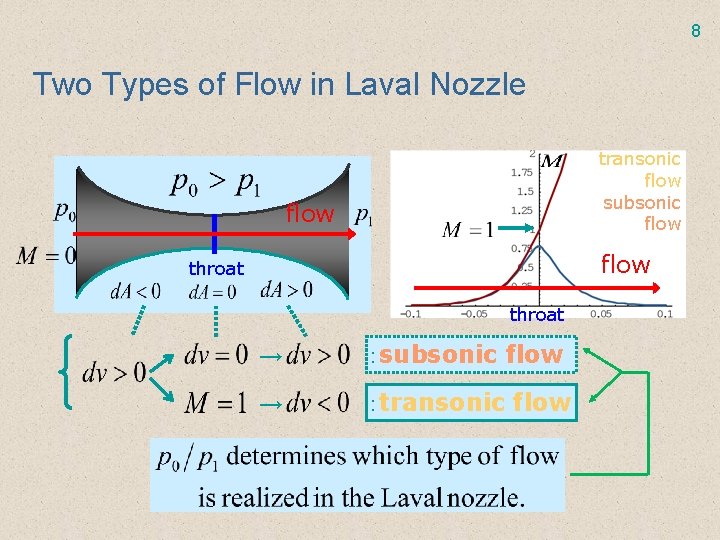
8 Two Types of Flow in Laval Nozzle transonic flow subsonic flow 　throat → ：subsonic flow → ：transonic flow

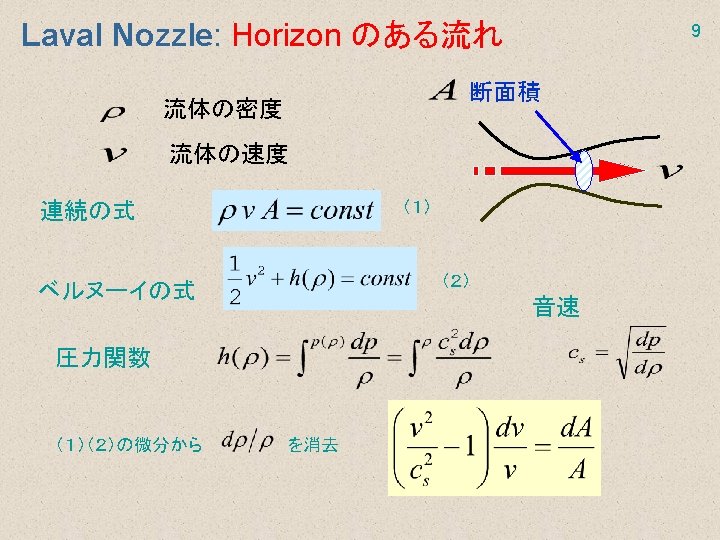
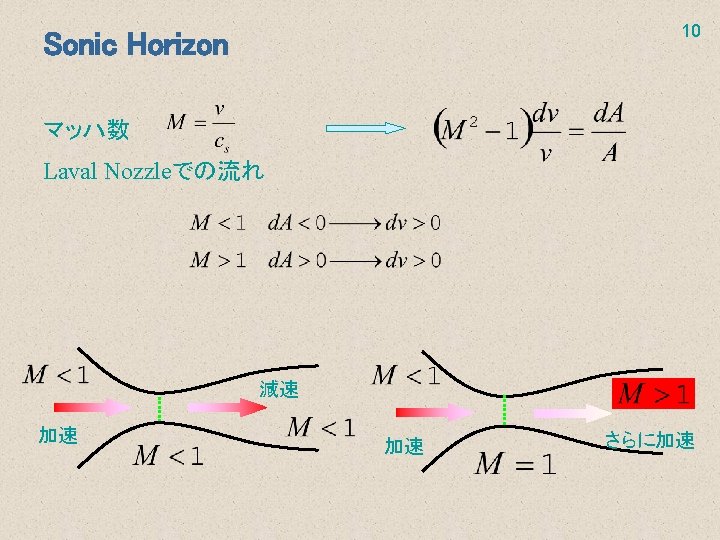
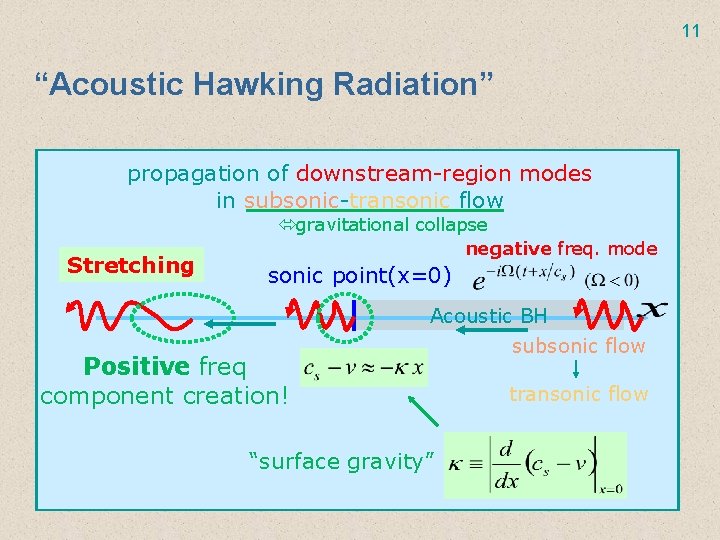
11 “Acoustic Hawking Radiation” propagation of downstream-region modes in subsonic-transonic flow Stretching gravitational collapse negative freq. mode sonic point(x=0) Positive freq component creation! Acoustic BH subsonic flow “surface gravity” transonic flow

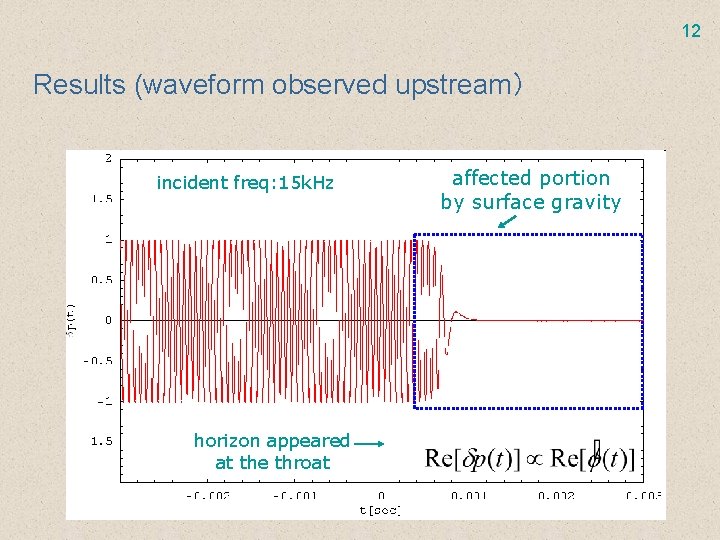
12 Results (waveform observed upstream） incident freq: 15 k. Hz horizon appeared at the throat affected portion by surface gravity

Spectrum of Acoustic Hawking Radiation (WKB analysis) Fourier component downstream region upstream region negative frequency positive frequency 13

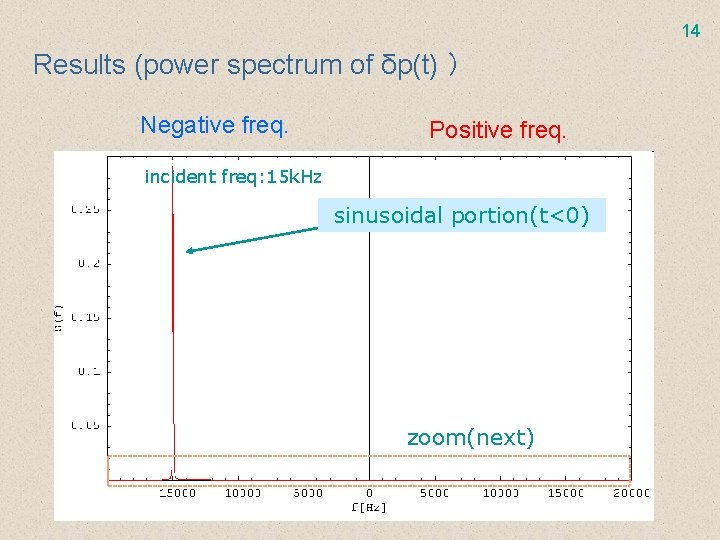
14 Results (power spectrum of δp(t) ） Negative freq. Positive freq. incident freq: 15 k. Hz sinusoidal portion(t<0) zoom(next)

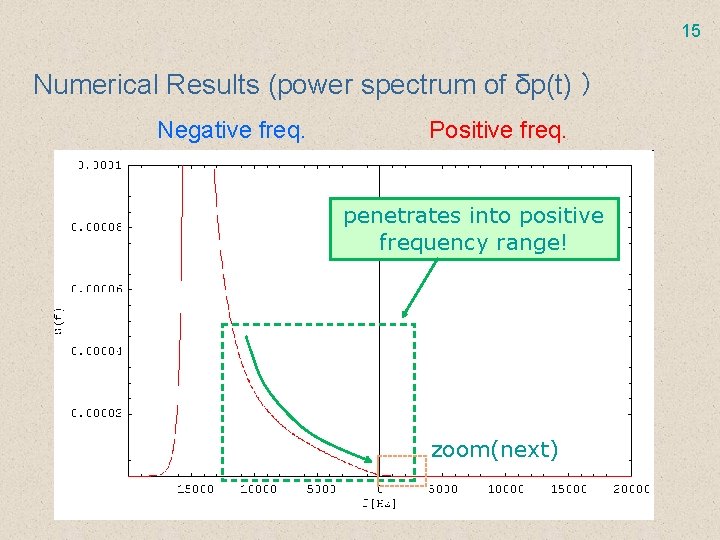
15 Numerical Results (power spectrum of δp(t) ） Negative freq. Positive freq. penetrates into positive frequency range! zoom(next)

16 Numerical Results (power spectrum of δp(t) ） Planckian fit

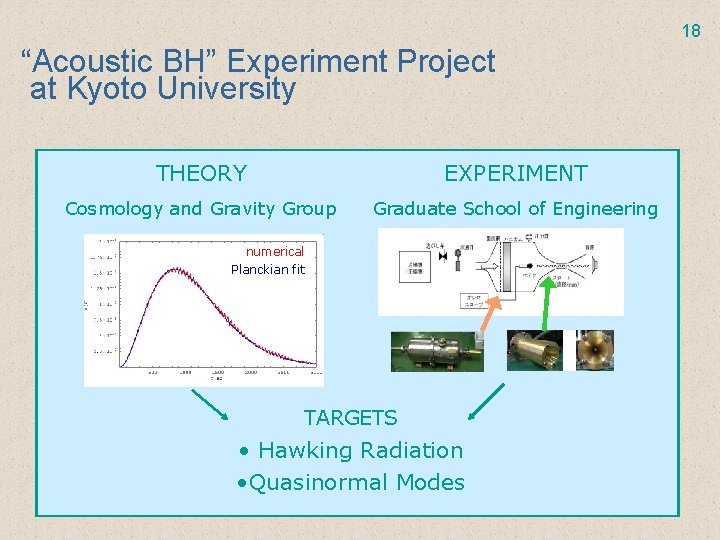
18 “Acoustic BH” Experiment Project　 at Kyoto University THEORY EXPERIMENT Cosmology and Gravity Group Graduate School of Engineering numerical Planckian fit TARGETS • Hawking Radiation • Quasinormal Modes

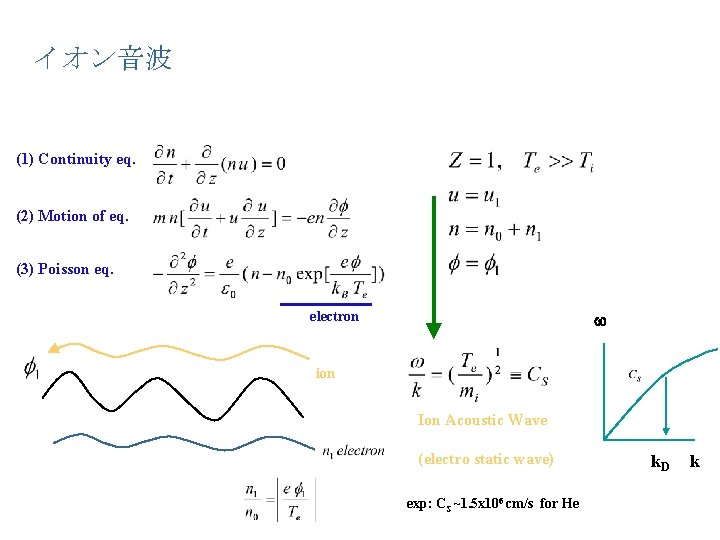
イオン音波 (1) Continuity eq. (2) Motion of eq. (3) Poisson eq. w electron ion Ion Acoustic Wave (electro static wave) exp: CS ~1. 5 x 106 cm/s for He k. D k

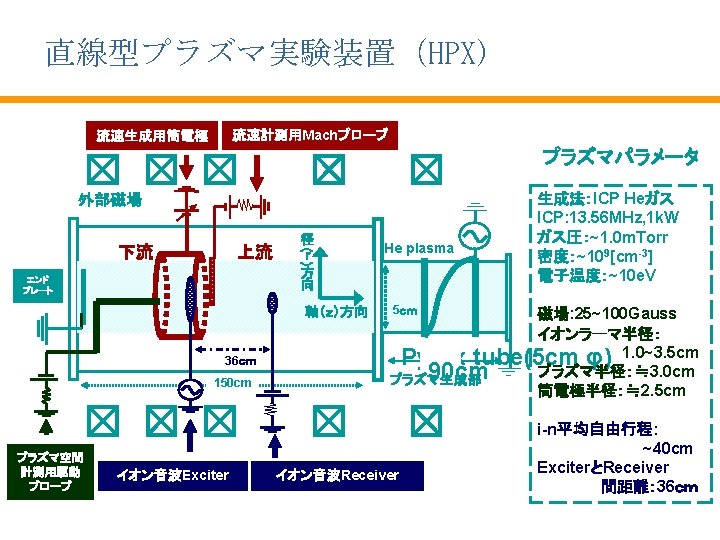
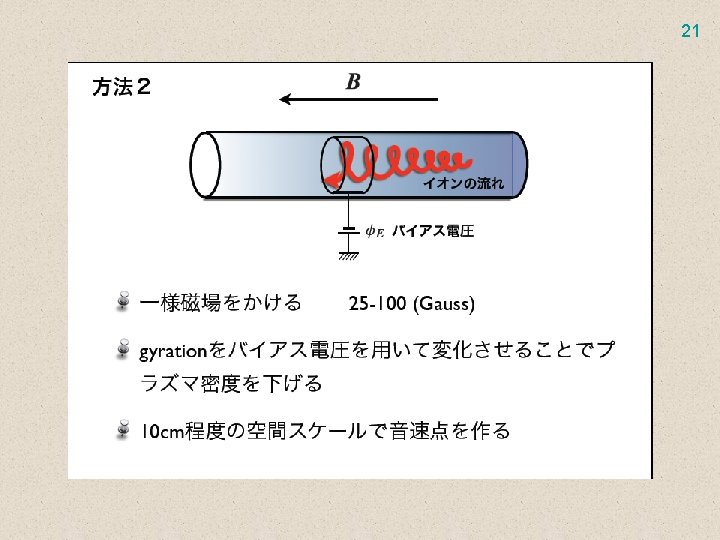
21

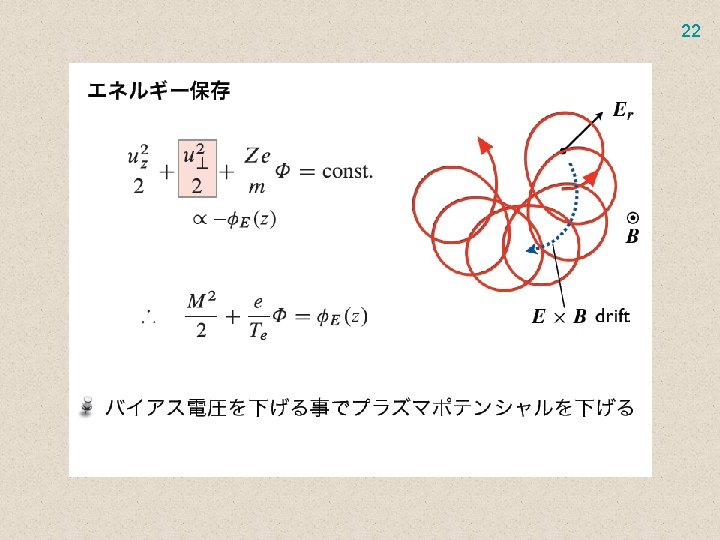
22

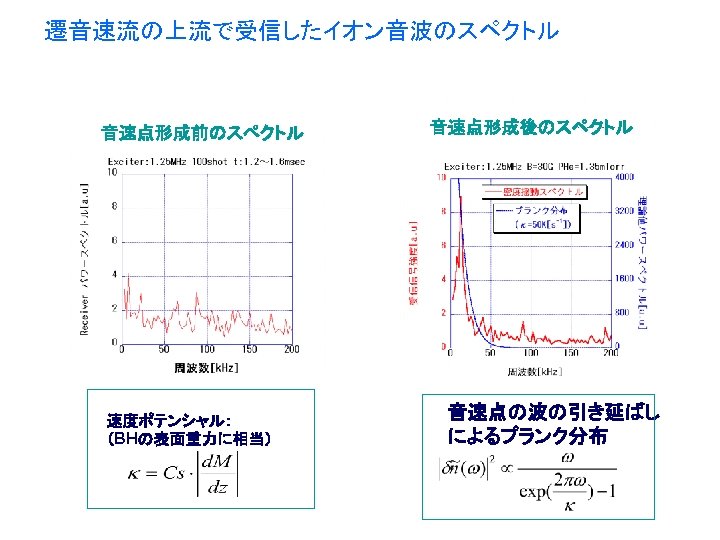
24 Numerical Simulation of Acoustic QN Ringing We perform two types of simulations: “Acoustic BH Formation” initial state: no flow set sufficiently large pressure difference final state: transonic flow ~ BH formation “Weak Shock Infall” initial state: transonic flow ‘shoot’ a weak shock into the flow final state: transonic flow ~ test particle infall

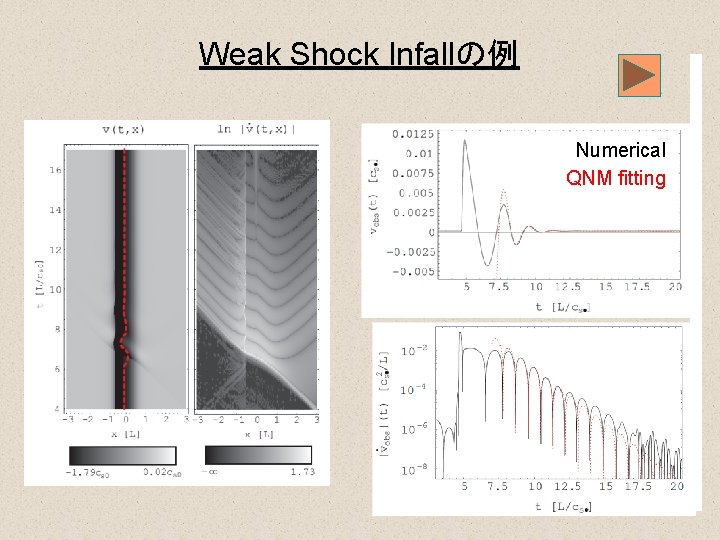
Weak Shock Infallの例 Numerical QNM fitting