Biznis statistika Predavanje 7 Statistiko ocjenjivanje Biznis statistika

Biznis statistika Predavanje 7 Statističko ocjenjivanje Biznis statistika – predavanje 7 24. 03. 2020.

Fokus predavanja § Konstruisati i interpretirati intervale povjerenja za aritmetičku sredinu § Određivanje veličine uzorka Biznis statistika – predavanje 7 24. 03. 2020.

Intervali povjerenja § Interval povjerenja aritmetičke sredine, μ § Kada je standardna devijacija populacije σ poznata § Kada standardna devijacija populacije σ nije poznata § Određivanje potrebne veličine uzorka Biznis statistika – predavanje 7 24. 03. 2020.
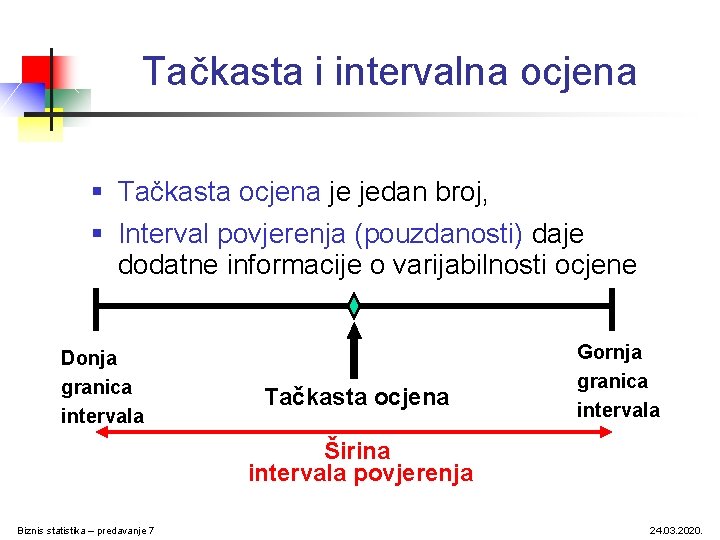
Tačkasta i intervalna ocjena § Tačkasta ocjena je jedan broj, § Interval povjerenja (pouzdanosti) daje dodatne informacije o varijabilnosti ocjene Donja granica intervala Tačkasta ocjena Gornja granica intervala Širina intervala povjerenja Biznis statistika – predavanje 7 24. 03. 2020.

Tačkaste ocjene Možemo ocijeniti parametar populacije … Aritmetička sredina Proporcija Biznis statistika – predavanje 7 na osnovu statistike uzorka (tačkasta ocjena) μ X π p 24. 03. 2020.

Intervali povjerenja § Kolika neizvjesnost prati tačkastu ocjenu parametra populacije? § Interval ocjene daje više informacija o karakteristikama populacije od tačkaste ocjene § Takvi intervali ocjene nazivaju se intervali povjerenja (ili pouzdanosti) Biznis statistika – predavanje 7 24. 03. 2020.

Interval povjerenja ocjene § Interval daje opseg vrijednosti: § Uzima u obzir varijacije statistika uzorka od uzorka do uzorka § Bazira se na opservacijama iz 1 uzorka § Daje informaciju o približnoj vrijednosti nepoznatog parametra populacije § Izražen preko nivoa (stepena) pouzdanosti § Nikad ne može biti 100% pouzdan Biznis statistika – predavanje 7 24. 03. 2020.

Proces ocjenjivanja Slučajan uzorak Populacija (aritmetička sredina, μ, nije poznata) Sredina X = 50 95% sam siguran da je μ između 40 & 60. Uzorak Biznis statistika – predavanje 7 24. 03. 2020.

Opšta formula § Opšta formula za sve intervale povjerenja je: Tačkasta ocjena ± (Kritična vrijednost)(Standardna greška) Biznis statistika – predavanje 7 24. 03. 2020.

Nivo pouzdanosti § Pouzdanost sa kojom interval sadrži nepoznati parametar populacije § U procentima (manje od 100%) Biznis statistika – predavanje 7 24. 03. 2020.

Nivo pouzdanosti, (1 - ) (nastavak) § Pretpostavimo nivo pouzdanosti od 95% § Zapisuje se i kao (1 - ) = 0. 95 § Interpretacija: § 95% svih intervala pouzdanosti koji se mogu konstruisati sadržaće nepoznati pravi parametar § Određeni interval može da sadrži ili može da ne sadrži pravi parametar § Vjerovatnoća se ne odnosi na specifični interval Biznis statistika – predavanje 7 24. 03. 2020.
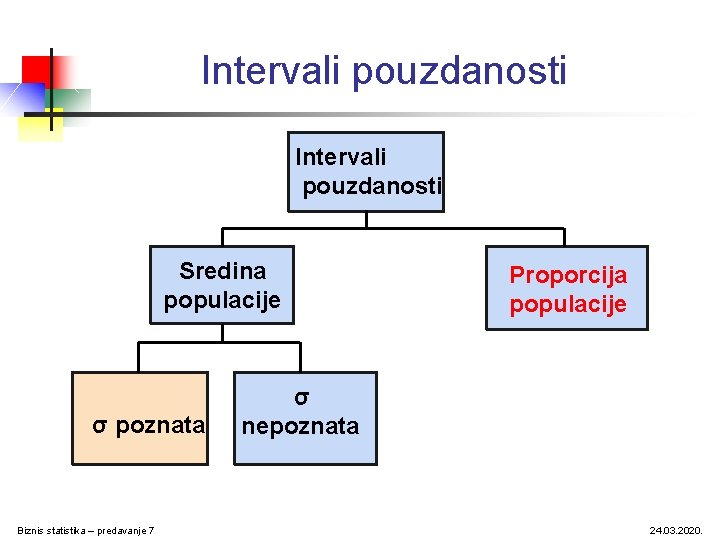
Intervali pouzdanosti Sredina populacije σ poznata Biznis statistika – predavanje 7 Proporcija populacije σ nepoznata 24. 03. 2020.

Interval povjerenja μ (σ poznata) § Pretpostavke § Standardna devijacija populacije σ je poznata § Populacija je normalno raspoređena § Ako populacija nije normalna, koristiti veliki uzorak § Interval povjerenja ocjene: gdje je tačkasta ocjena Z je kritična distribucija normalne distribucije za vjerovatnoću /2 dvostrano je standardna greška Biznis statistika – predavanje 7 24. 03. 2020.

Određivanje kritične vrijednosti, Z § Posmatrajte 95% interval povjerenja: Z jedinice: X jedinice: Biznis statistika – predavanje 7 Z= -1. 96 Donja granica pouzdanosti 0 Tačkasta ocjena Z= 1. 96 Gornja granica pouzdanosti 24. 03. 2020.

Često korišćeni nivoi pouzdanosti § Najčešće se koriste nivoi pouzdanosti od 90%, 95% i 99% Nivo pouzdanosti 80% 95% 98% 99. 9% Biznis statistika – predavanje 7 Koeficijent pouzdanosti, 0. 80 0. 95 0. 98 0. 998 0. 999 Z vrijednost 1. 28 1. 645 1. 96 2. 33 2. 58 3. 08 3. 27 24. 03. 2020.

Intervali i nivo pouzdanosti Uzoračka distribucija aritmetičke sredine x Interval obuhvata x 1 x 2 do Intervali pouzdanosti Biznis statistika – predavanje 7 (1 - )x 100% od konstruisanog intervala sadrži μ; ( )x 100% ne sadrži. Chap 8 -16

Primjer § Uzorak od 11 elektro kola odabran je iz velike normalne populacije i ima prosječan otpor od 2. 20 oma. Na osnovu prethodnih testova poznato je da populacija ima standardnu devijaciju 0. 35 oma. § Odredi interval povjerenja od 95% za prosječni otpor populacije. Biznis statistika – predavanje 7 24. 03. 2020.

Primjer (nastavak) § Rešenje: Biznis statistika – predavanje 7 24. 03. 2020.

Interpretacija § Sa pouzdanošću od 95% prava aritmetička sredina otpora je između 1. 9932 i 2. 4068 oma § Iako prava aritmetička sredina može ali ne mora da bude u ovom interalu, 95% intervala određenih na ovaj način sadržaće pravu aritmetičku sredinu Biznis statistika – predavanje 7 24. 03. 2020.

Intervali povjerenja Sredina populacije σ poznata Proporcija populacije σ nepoznata Basic Business Statistics, 10 e © 2006 Prentice-Hall, Inc. 24. 03. 2020.

Interval povjerenja za μ (σ nije poznata) § Ukoliko standardna devijacije populacije σ nije poznata, zamjenjujemo je standardnom devijacijom uzorka, S § To povećava neizvjesnost, pošto S varira od uzorka do uzorka § Tada se koristi t distribucija umjesto normalne distribucije Biznis statistika – predavanje 7 24. 03. 2020.

Interval povjerenja za μ (σ nije poznata) (nastavak) § Pretpostavke § Standardna devijacija populacije nije poznata § Populacija ima normalnu distribuciju § Ukoliko populacija nije normalna, koristiti veliki uzorak § Koristiti Studentovu t distribuciju § Interval povjerenja: (gdje je t kritična vrijednost t distribucije za (n -1) stepen slobode i α prag značajnosti) Biznis statistika – predavanje 7 24. 03. 2020.

Studentova t distribucija § Studentova t distribucija predstavlja porodicu distribucija § t vrijednost zavisi od broja stepeni slobode(s. s. ) § Broj nezavisnih vrijednosti (opservacija) u uzorku, umanjen za broj ogranjičenja koja se nameću ovim vrijednostima s. s. = n - 1 Biznis statistika – predavanje 7 24. 03. 2020.

Stepeni slobode (s. s. ) Ideja: Broj opservacija koje mogu varirati nakon što se izračuna aritmetička sredina uzorka Primjer: Pretpostavimo da je sredina tri broja 8. 0 Neka je X 1 = 7 Neka je X 2 = 8 Koliko je X 3? Ako je sredina ove tri vrijednosti 8. 0, onda X 3 mora biti 9 (tj. X 3 ne može da varira) Ovdje, n = 3, pa je broj stepeni slobode = n – 1 = 3 – 1 = 2 (Dvije vrijednosti mogu biti bilo koje, ali treća vrijednost ne može varirati za datu sredinu) Biznis statistika – predavanje 7 24. 03. 2020.

Studentova t distribucija Primijetite da: t Z kako n raste Standardna normalna (t sa s. s. = ∞) t (s. s. = 13) t-distribucija ima oblik zvona i simetrična je, ali je spljoštenija, ima ‘deblje’ repove od normalne t (s. s. = 5) 0 Biznis statistika – predavanje 7 t 24. 03. 2020.
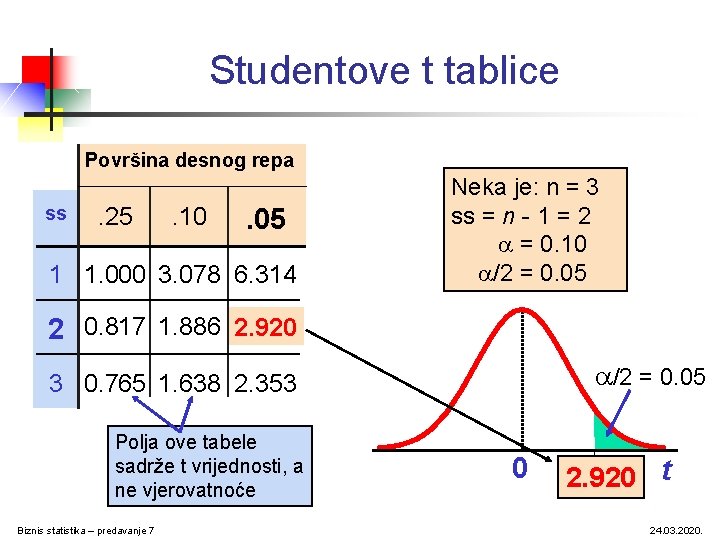
Studentove t tablice Površina desnog repa ss . 25 . 10 . 05 1 1. 000 3. 078 6. 314 Neka je: n = 3 ss = n - 1 = 2 = 0. 10 /2 = 0. 05 2 0. 817 1. 886 2. 920 /2 = 0. 05 3 0. 765 1. 638 2. 353 Polja ove tabele sadrže t vrijednosti, a ne vjerovatnoće Biznis statistika – predavanje 7 0 2. 920 t 24. 03. 2020.

Vrijednosti t distribucije U poređenju sa Z vrijednostima Nivo t pouzdanosti (10 s. s. ) t (20 s. s. ) t (30 s. s. ) Z ____ 0. 80 1. 372 1. 325 1. 310 1. 28 0. 90 1. 812 1. 725 1. 697 1. 645 0. 95 2. 228 2. 086 2. 042 1. 96 0. 99 3. 169 2. 845 2. 750 2. 58 Zapazite: t Biznis statistika – predavanje 7 Z kako se n povećava 24. 03. 2020.

Primjer Slučajni uzorak od n = 25 ima X = 50 i S = 8. Odredi interval povjerenja od 95% za μ § s. s. = n – 1 = 24, pa Interval povjerenja je 46. 698 ≤ μ ≤ 53. 302 Biznis statistika – predavanje 7 24. 03. 2020.
Određivanje veličine uzorka Za sredinu Biznis statistika – predavanje 7 Za proporciju 24. 03. 2020.

Greška uzorka § Potrebna veličina uzorka može se odrediti tako da se postigne greška uzorka (e) sa određenim nivoom pouzdanosti (1 - ) § Greška uzorka § Nepreciznost u ocjeni parametra populacije § Veličina koja se dodaje i oduzima od tačkaste ocjene da bi se odredio interval povjerenja Biznis statistika – predavanje 7 24. 03. 2020.

Određivanje veličine uzorka Za sredinu Biznis statistika – predavanje 7 Greška uzorka 24. 03. 2020.

Određivanje veličine uzorka (nastavak) Određivanje veličine uzorka Za sredinu Riješiti po n da se dobije Biznis statistika – predavanje 7 24. 03. 2020.

Određivanje veličine uzorka (nastavak) § Da bi se odredila potrebna veličina uzorka za kalkulisanje aritmetičke sredine, mora se znati: § Željeni nivo pouzdanosti (1 - ), koji determiniše kritičnu Z vrijednost § Prihvatljiva greška uzorka, e § Standardna devijacija, σ Biznis statistika – predavanje 7 24. 03. 2020.
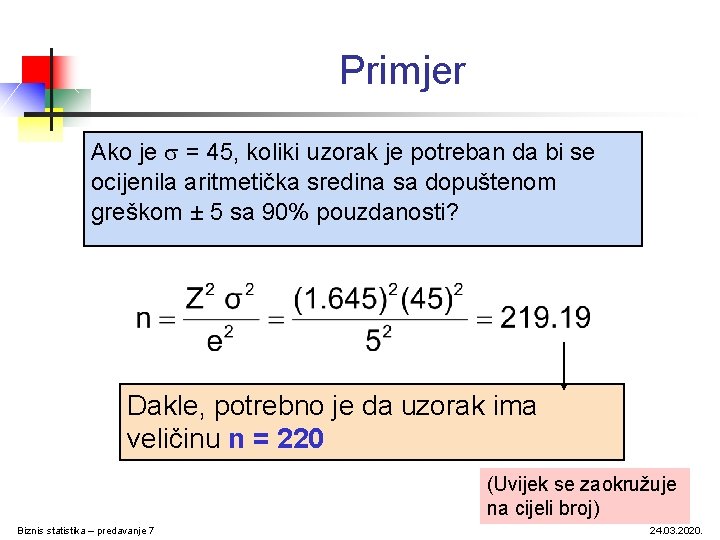
Primjer Ako je = 45, koliki uzorak je potreban da bi se ocijenila aritmetička sredina sa dopuštenom greškom ± 5 sa 90% pouzdanosti? Dakle, potrebno je da uzorak ima veličinu n = 220 (Uvijek se zaokružuje na cijeli broj) Biznis statistika – predavanje 7 24. 03. 2020.

Ako je σ nepoznata § Ako σ nije poznata, može se ocijeniti koristeći formulu za veličinu uzorka § Koristiti vrijednost σ za koju se očekuje da bude makar koliko i prava σ § Odabrati pilot uzorak i ocijeniti σ koristeći standardnu devijaciju uzorka, S Biznis statistika – predavanje 7 24. 03. 2020.

Etička pitanja § Intervale povjerenja za ocjene parametara uvijek bi trebalo odrediti i navesti kada se izvještava u tačkastoj ocjeni § Uvijek treba navesti nivo pouzdanosti sa kojim se radi § Treba informisati i o veličini uzorka § Trebalo bi obezbijediti tumačenje - interpretaciju Biznis statistika – predavanje 7 24. 03. 2020.

Rezime § § § Koncept intervala povjerenja Diskusija o tačkastoj ocjeni Konstruisanje intervala povjerenja Intervali povjerenja za sredinu kada je σ poznata Intervali povjerenja za sredinu σ nije poznata Determinisanje potrebne veličine uzorka za ocjenu sredine i populacije Biznis statistika – predavanje 7 24. 03. 2020.
- Slides: 37