Biznis statistika Predavanje 6 Jednostavna linearna regresija Biznis

Biznis statistika Predavanje 6 Jednostavna linearna regresija Biznis statistika - Predavanje 6 22. 04. 2020.

Fokus predavanja § Kako na osnovu regresione analize i vrijednosti nezavisne varijable predviđati vrijednost zavisne varijable § Značenje regresionih koeficijenata b 0 i b 1 § Zaključivanje u vezi sa koeficijentom pravca i koeficijentom korelacije § Ocjena srednje vrijednosti Y i predviđanje pojedinačnih vrijednosti Y Biznis statistika - Predavanje 6 22. 04. 2020.

Korelacija vs. Regresija § Dijagram rasturanja se može koristiti da pokaže relaciju između dvije varijable § Korelacija mjeri jačinu linearne veze između dvije varijable § Korelacija se bavi jačinom veze § Korelacija se ne bavi pitanjem kauzalnosti Biznis statistika - Predavanje 6 22. 04. 2020.

Uvod u regresionu analizu § Regresiona analiza se koristi za: § Predviđanje vrijednosti zavisne varijable na osnovu vrijednosti makar jedne nezavisne varijable § Objašnjavanje efekata promjena nezavisne varijable na zavisnu promjenljivu Zavisna varijabla: varijabla koju želimo da objasnimo ili predviđamo Nezavisna varijabla: varijabla koja se koristi da za objašnjavanje zavisne varijable Biznis statistika - Predavanje 6 22. 04. 2020.

Model jednostavne linearne regresije § Samo jedna nezavisna varijabla, X § Relacija između X i Y se opisuje linearnom funkcijom § Pretpostavlja se da su promjene u Y izazvane promjenama u X Biznis statistika - Predavanje 6 22. 04. 2020.

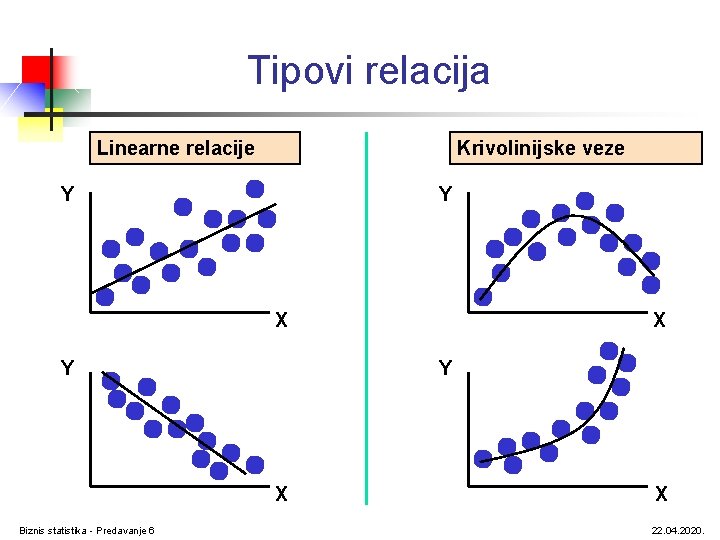
Tipovi relacija Linearne relacije Krivolinijske veze Y Y X Biznis statistika - Predavanje 6 X X 22. 04. 2020.

Tipovi relacija (nastavak) Snažne relacije Slabe relacije Y Y X Biznis statistika - Predavanje 6 X X 22. 04. 2020.

Tipovi relacija (nastavak) Nema relacije Y X Biznis statistika - Predavanje 6 22. 04. 2020.

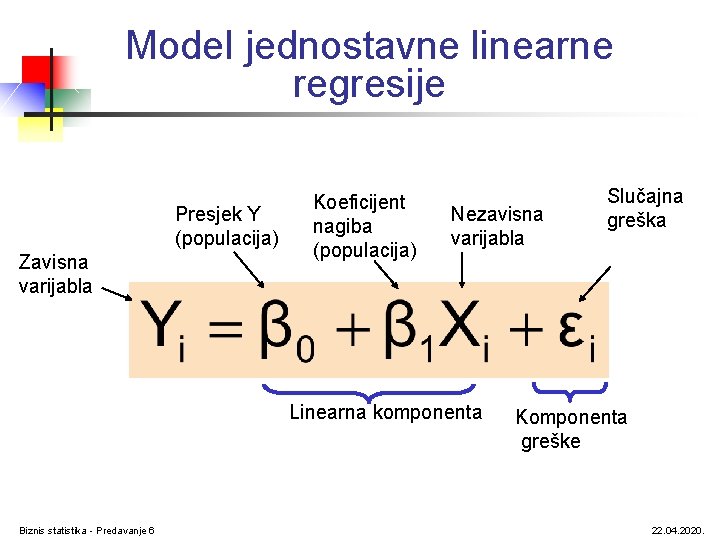
Model jednostavne linearne regresije Presjek Y (populacija) Zavisna varijabla Koeficijent nagiba (populacija) Nezavisna varijabla Linearna komponenta Biznis statistika - Predavanje 6 Slučajna greška Komponenta greške 22. 04. 2020.

Model jednostavne linearne regresije (nastavak) Y Opservirana (prava) vrijednost Y za Xi εi Predviđena (ocijenjena) vrijednost Y za Xi Nagib = β 1 Greška za vrijednost Xi Presjek = β 0 Xi Biznis statistika - Predavanje 6 X 22. 04. 2020.

Jednačina jednostavne linearne regresije (Regresiona prava) Jednačina jednostavne linearne regresije daje ocjenu regresione prave populacije Ocijenjena (ili predviđena) Y vrijednost za opservaciju i Ocjena regresionog presjeka Ocjena regresionog nagiba Vrijednost X za opservaciju i Očekivana vrijednost greške ei je nula Biznis statistika - Predavanje 6 22. 04. 2020.

Metod najmanjih kvadrata § b 0 i b 1 vrijednosti se dobijaju tako što se minimizira suma kvadrata razlika između Y i Biznis statistika - Predavanje 6 22. 04. 2020.

Metod najmanjih kvadrata § Koeficijenti b 0 i b 1 dobijaju se primjenom formula Biznis statistika - Predavanje 6 22. 04. 2020.

Interpretacija presjeka i nagiba § b 0 je ocijenjena prosječna vrijednost Y kada je vrijednost X jednaka nula § b 1 je ocijenjena promjena prosječne vrijednosti Y kao rezultat jedinične promjene X Biznis statistika - Predavanje 6 22. 04. 2020.

Mjere varijacije § Ukupna varijacija ima dvije komponente: Ukupna suma kvadrata Regresiona suma kvadrata Suma kvadrata grešaka gdje: = prosječna vrijednost zavisne varijable Yi = Opservirana vrijednost zavisne varijable i Biznis statistika - Predavanje 6 = Predviđena vrijednost Yza datu Xi vrijednost 22. 04. 2020.

Mjere varijacije (nastavak) § SST = ukupna suma kvadrata § Mjeri varijaciju Yi vrijednosti oko njihove sredine Y § SSR = regresiona suma kvadrata § Objašnjava varijacije koje se pripisuju odnosu između Xi. Y § SSE = suma kvadrata grešaka § Varijacije su izazvane nekim drugim faktorima a ne relacijom između X i Y Biznis statistika - Predavanje 6 22. 04. 2020.

Mjere varijacije (nastavak) Y Yi SSE = (Yi - Yi )2 _ Y Y SST = (Yi - Y)2 _ SSR = (Yi - Y)2 _ Y Xi Biznis statistika - Predavanje 6 _ Y X 22. 04. 2020.

Koeficijent determinacije, R 2 § Koeficijent determinacije mjeri dio ukupnih varijacija zavisne promjenljive koji je objašnjen varijacijama nezavisne varijable § Koeficijent determinacije se naziva R na kvadrat, R 2 pažnja: Biznis statistika - Predavanje 6 22. 04. 2020.

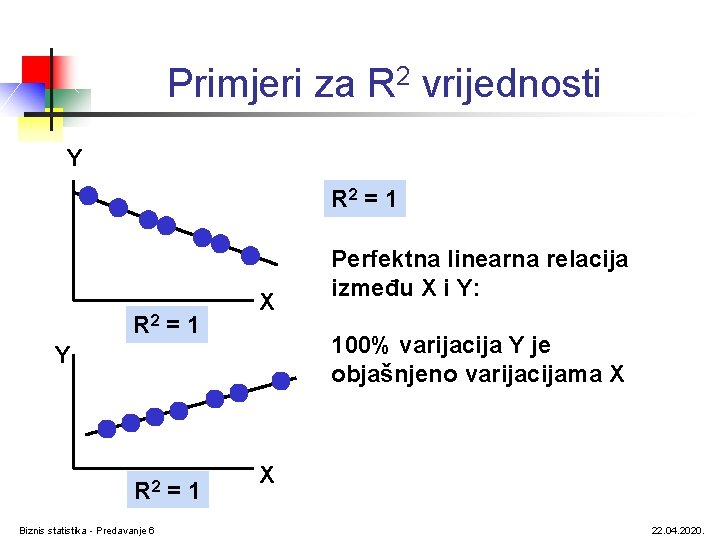
Primjeri za R 2 vrijednosti Y R 2 = 1 X 100% varijacija Y je objašnjeno varijacijama X Y R 2 Biznis statistika - Predavanje 6 =1 Perfektna linearna relacija između X i Y: X 22. 04. 2020.

Primjeri za R 2 vrijednosti Y 0 < R 2 < 1 X Slabija linearna veza između X i Y: Dio ali ne sve varijacije Y objašnjen je varijacijama X Y X Biznis statistika - Predavanje 6 22. 04. 2020.

Primjeri za R 2 vrijednosti R 2 = 0 Y Nema linearne veze između X i Y: R 2 = 0 Biznis statistika - Predavanje 6 X Vrijednost Y ne zavisi od X. (Nimalo varijacija. Y nije objašnjeno varijacijama X. ) 22. 04. 2020.

Standardna greška regresije § Standardna devijacija varijacija opservacija oko regresione linije izračunava se prema formuli gdje SSE = suma kvadrata grešaka n = veličina uzorka Biznis statistika - Predavanje 6 22. 04. 2020.

Upoređivanje standardnih grešaka SYX mjeri varijacije opserviranih Y vrijednosti oko regresione linije Y Y X X Veličinu SYX trebalo bi uvijek vrednovati relativno u odnosu na Y vrijednosti u uzorku Biznis statistika - Predavanje 6 22. 04. 2020.

Nagib regresije § Standardna greška regresionog koeficijenta nagiba (b 1) ocjenjuje se formulom gdje: = standardna greška ocjene koeficijenta nagiba – metod ONK = Standardna greška regresije Biznis statistika - Predavanje 6 22. 04. 2020.

Upoređivanje standardnih grešaka koeficijenta pravca mjeri varijaciju nagiba regresionih linija iz različitih uzoraka koji se mogu odrediti Y Y X Biznis statistika - Predavanje 6 X 22. 04. 2020.

Razmatranje koeficijenta pravca: t test § t test za nagib regresije populacije § Postoji li linearna veza između X i Y? § Nulta i alternativna hipoteza H 0: β 1 = 0 H 1: β 1 0 (nema linearne veze) (linearna veza postoji) § Test statistika gdje: b 1 = ocijenjeni koeficijent pravca regresije β 1 = nagib prave populacije Sb 1= standardna greška ocjene koeficijenta nagiba Biznis statistika - Predavanje 6 22. 04. 2020.

Interval povjerenja ocjene koeficijenta pravca Interval povjerenja koeficijenta pravca: s. s. = n - 2 Biznis statistika - Predavanje 6 22. 04. 2020.

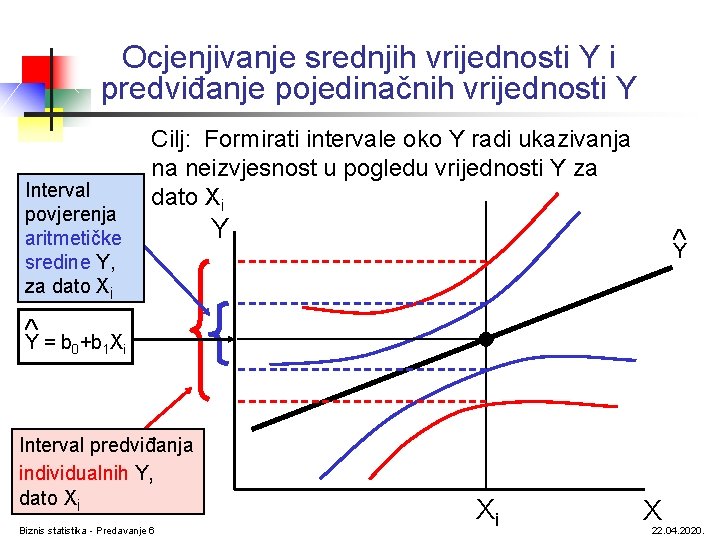
Ocjenjivanje srednjih vrijednosti Y i predviđanje pojedinačnih vrijednosti Y Interval povjerenja aritmetičke sredine Y, za dato Xi Cilj: Formirati intervale oko Y radi ukazivanja na neizvjesnost u pogledu vrijednosti Y za dato Xi Y Y Y = b 0+b 1 Xi Interval predviđanja individualnih Y, dato Xi Biznis statistika - Predavanje 6 Xi X 22. 04. 2020.

Interval povjerenja za sredinu promjenljive Y, za dato X Interval povjerenja za srednju vrijednost Y za datu vrijednost Xi Veličina intervala varira u skladu sa udaljenosti od sredine, X. Biznis statistika - Predavanje 6 22. 04. 2020.

Interval predviđanja za pojedinačne vrijednosti Y, za dato X Interval povjerenja za individualne vrijednosti Y za date vrijednosti Xi Ovo se dodaje širini intervala da bi se izrazila neizvjesnost u pogledu svake pojedinačne situacije Biznis statistika - Predavanje 6 22. 04. 2020.

Strategije za izbjegavanje nedostataka regresije § Početi sa dijagramom rasturanja X vs. Y radi observiranja moguće relacije zavisnosti § Provjeriti da li su ispunjene pretpostavke § Ako neka pretpostavka nije ispunjena koristiti neki drugi metod ocjenjivanja umjesto ONK Biznis statistika - Predavanje 6 22. 04. 2020.

Strategije za izbjegavanje nedostataka regresije (nastavak) § Testirati značajnost ocjena regresionih koeficijenata i konstruisati intervale povjerenja § Ne predviđati za vrijednosti izvan relevantnog opsega Biznis statistika - Predavanje 6 22. 04. 2020.