Bivariate Data Introduction Describing Relationships How would you

Bivariate Data Introduction

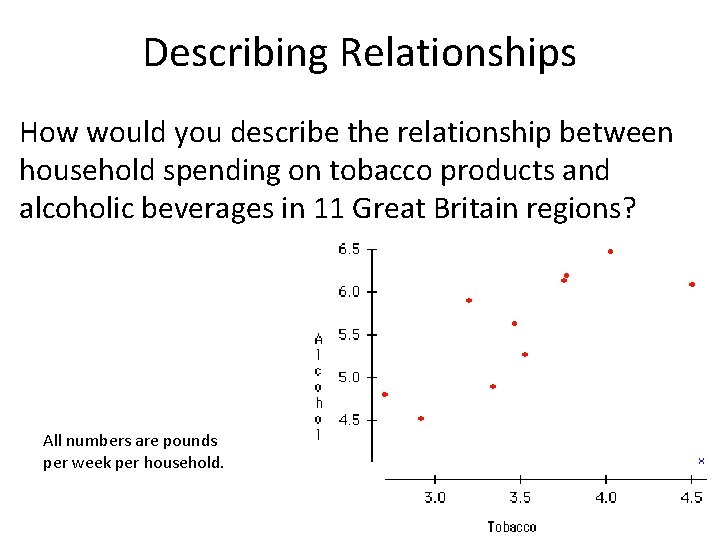
Describing Relationships How would you describe the relationship between household spending on tobacco products and alcoholic beverages in 11 Great Britain regions? All numbers are pounds per week per household.

Describing Relationships Two variables: • Response variable (y): the variable we are trying to measures as an outcome of a study or experiment. This responds to the other variable (x). It is also the variable we will try to predict. • Explanatory variable (x): a variable that may help explain changes in a response variable. • Example: in the previous slide, neither tobacco spending nor alcohol spending respond to the other variable, so we will not call one the response or explanatory. But, since we want to predict alcohol spending, we will put that on the y-axis.

Scatterplots • Scatterplots – a graph on the x-y coordinate plane that shows a point for each observation with its value for x and y.

Describing Scatterplots Describing scatterplots: • Direction • Form • Strength • Outliers/Influential Points

Describing Scatterplots Direction: • Positive association – when one variable increases, the other variable increases (think: positive slope) • Negative association – when one variable increases, the other variable decreases (think: negative slope)

Describing Scatterplots Form • Function family (linear or not)

Describing Scatterplots Strength • How close are the points to a clear form?

Describing Scatterplots Outliers: • Is there a point that would be very far from the best fit equation? Outliers on a scatterplot are unusual in the y-variable. (there is no mathematical calculation like there is for one-variable data) Outlier! So far from the line!

Describing Scatterplots Influential Point: • Is there a point that would pull the regression line towards it? Influential points on a scatterplot are unusual in the x-variable. These will pull the regression line to the point. (there is no mathematical calculation like there is for one-variable data) Influential Point! So far to the right!

Association Script • We have a script to describe the relationship we see on a scatterplot. It goes like this: The association between x-variable and yvariable is pos/neg and strength form. • Outliers and influential observations are important to consider, but you will likely be asked about these directly.

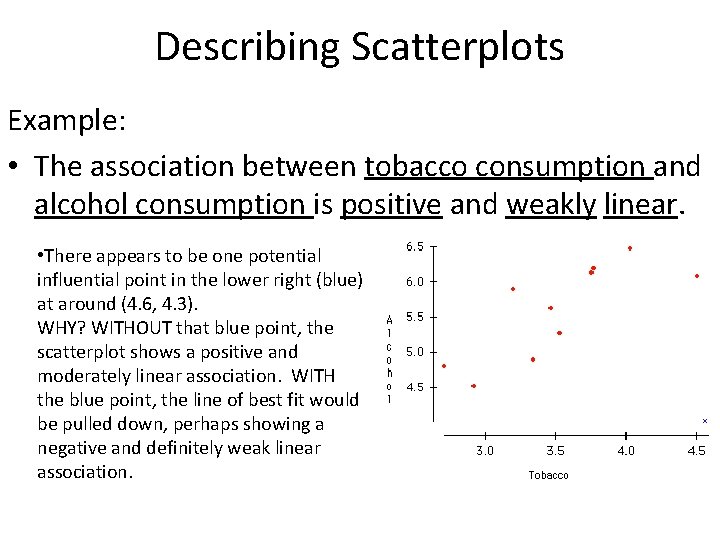
Describing Scatterplots Example: • The association between tobacco consumption and alcohol consumption is positive and weakly linear. • There appears to be one potential influential point in the lower right (blue) at around (4. 6, 4. 3). WHY? WITHOUT that blue point, the scatterplot shows a positive and moderately linear association. WITH the blue point, the line of best fit would be pulled down, perhaps showing a negative and definitely weak linear association.