Bipartite graphs and Planar Graphs No edges crossing

Bipartite graphs and Planar Graphs No edges crossing

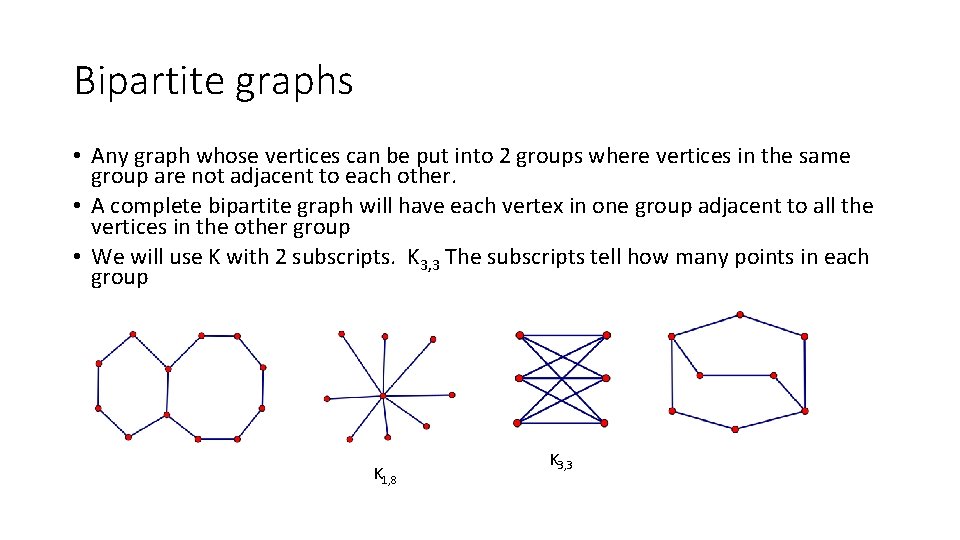
Bipartite graphs • Any graph whose vertices can be put into 2 groups where vertices in the same group are not adjacent to each other. • A complete bipartite graph will have each vertex in one group adjacent to all the vertices in the other group • We will use K with 2 subscripts. K 3, 3 The subscripts tell how many points in each group K 1, 8 K 3, 3

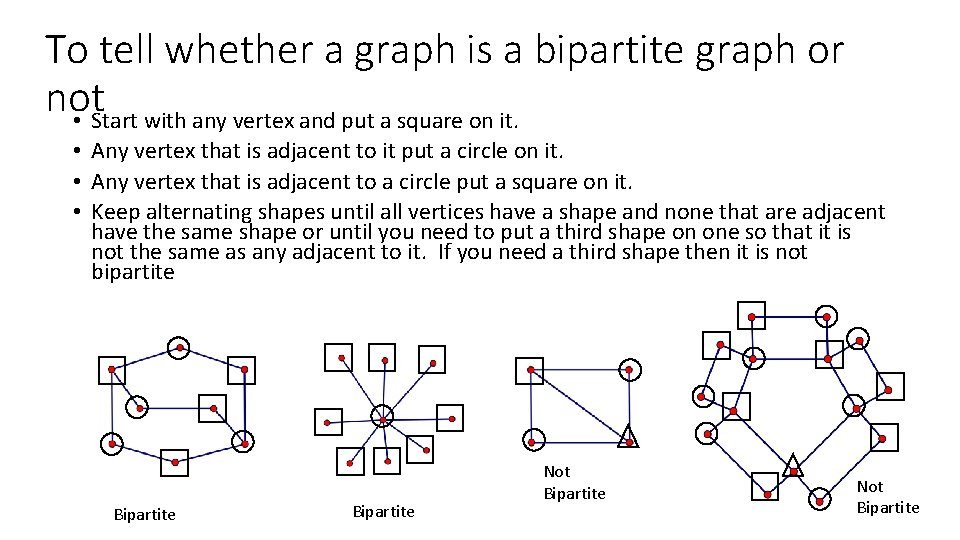
To tell whether a graph is a bipartite graph or not • Start with any vertex and put a square on it. • Any vertex that is adjacent to it put a circle on it. • Any vertex that is adjacent to a circle put a square on it. • Keep alternating shapes until all vertices have a shape and none that are adjacent have the same shape or until you need to put a third shape on one so that it is not the same as any adjacent to it. If you need a third shape then it is not bipartite Bipartite Not Bipartite

Planar graphs • Any graph that can be redrawn without any of it edges crossing is a planar graph. • Any graph that can’t (of a reasonable size) will have a K 5 or a K 3, 3 as a subgraph. • Reminder • A K 5 is a graph with 5 vertices that are adjacent to all other vertices. • A K 3, 3 is complete bipartite graph

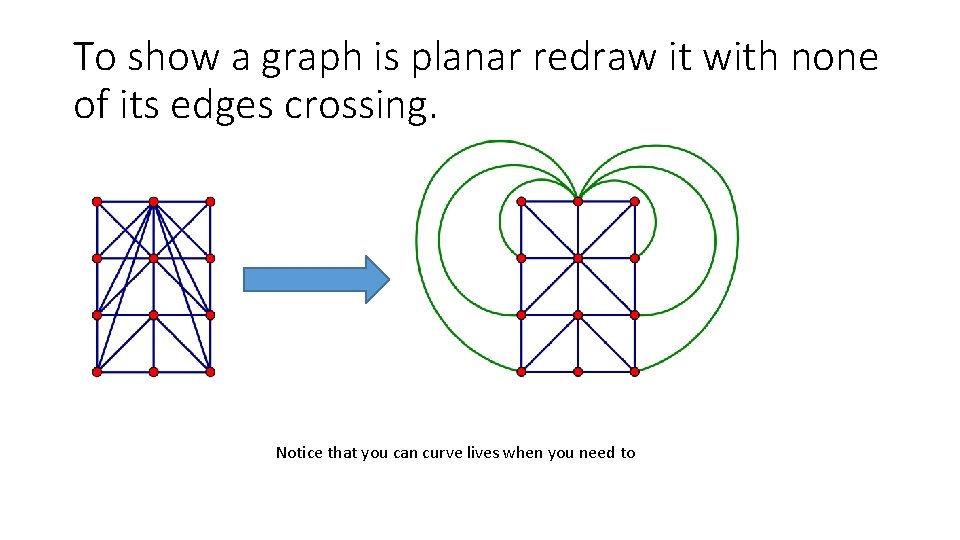
To show a graph is planar redraw it with none of its edges crossing. Notice that you can curve lives when you need to

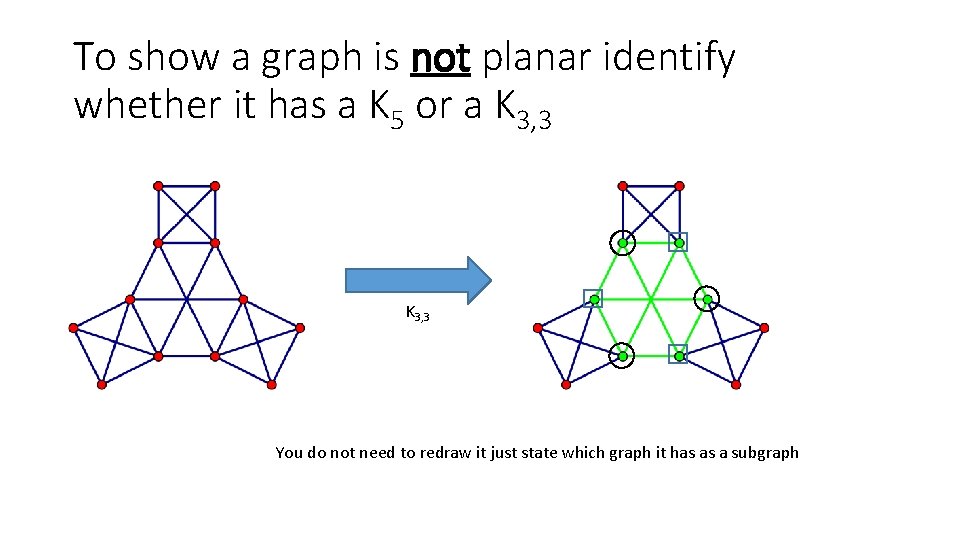
To show a graph is not planar identify whether it has a K 5 or a K 3, 3 You do not need to redraw it just state which graph it has as a subgraph