BIOSTATISTICS Confidence Interval Ayesha Abdullah THE NORMAL DISTRIBUTION

BIOSTATISTICS Confidence Interval Ayesha Abdullah

THE NORMAL DISTRIBUTION Study of Frequency distribution of a variable can be very informative in summarizing and analyzing data. Normal or bell shaped distribution, skewed distributions, bimodal distributions etc. Even if a variable in not normally distributed its mean would be. Data that demonstrate a normal distribution can be analysed using parametric methods of statistical testing 2 and constructing confidence intervals.

POINT ESTIMATE AND INTERVAL ESTIMATE A specific numerical value estimate of a parameter e. g. the mean is a point estimate An interval of range of values used to estimate the parameter is the interval estimate The probability that the range (obtained from the sample) contains the population parameter is the confidence level The interval estimate made at a specified level of confidence for a particular parameter is the confidence interval 3

THE NORMAL DISTRIBUTION Two important mathematical properties of the normal distribution are: � it is symmetric about the mean, and � approximately 95% of the data points lie within 2 standard deviations of the mean. 4
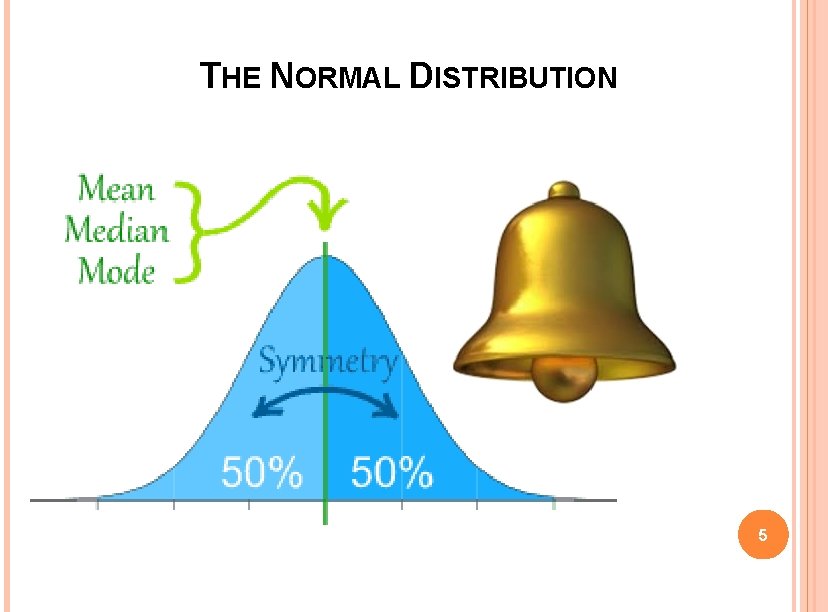
THE NORMAL DISTRIBUTION 5
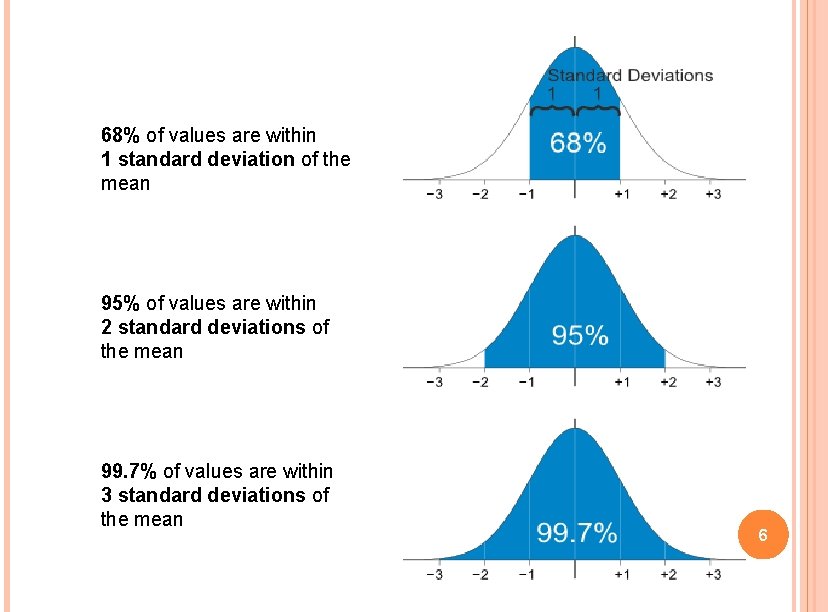
68% of values are within 1 standard deviation of the mean 95% of values are within 2 standard deviations of the mean 99. 7% of values are within 3 standard deviations of the mean 6
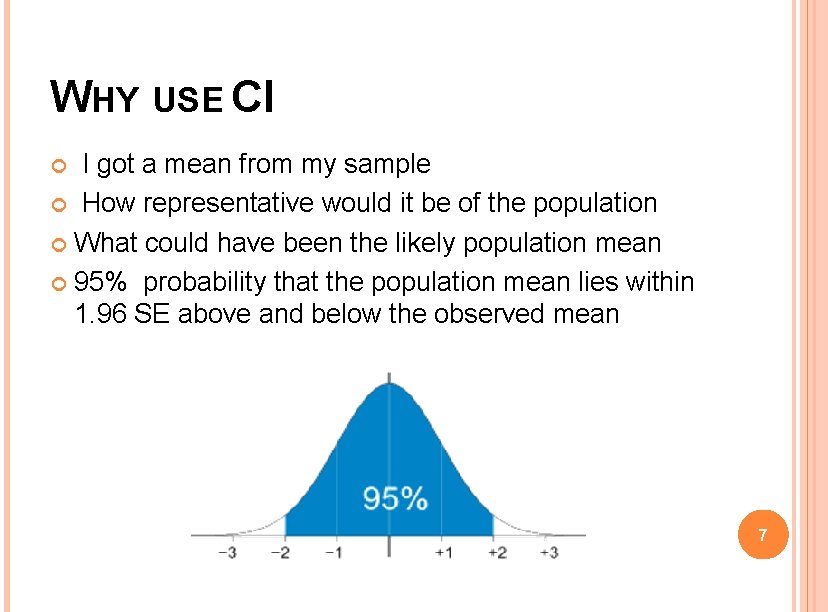
WHY USE CI I got a mean from my sample How representative would it be of the population What could have been the likely population mean 95% probability that the population mean lies within 1. 96 SE above and below the observed mean 7

CONFIDENCE INTERVALS Since we are working with samples we wish to know how precise our estimate form the sample is so that we can generalize the results to the reference population from which the sample was taken It can be done by calculating confidence intervals and applying statistical tests of significance CI can be calculated for � 95% confidence [5% imprecision] � 99% confidence [1 % imprecision ] � 90% confidence [10 % imprecision ] 8

WHAT DO WE NEED FOR CALCULATINGCI Standard Deviation=SD or S Sample size =n Calculate Standard error of the mean (SEM) by 95% CI= Mean ± 1. 96 (SEM) 99% CI= Mean ± 2. 58 (SEM) 90% CI= Mean ± 1. 64 (SEM) 9

EXAMPLE Sample of 30 ICUs found that the average time age of a pulse oximeter was 5. 6 years. With a SD of 0. 8 year Calculate the 99% CI. 5. 6 -2. 58 [0. 8/ 30 ] + [2. 58[0. 8/ 30] 5. 6 - [0. 38] + [0. 38] 5. 22 to 5. 98 10

EXAMPLE Sample of 1513 babies with mean birth weight of 3325 g and SD of 528 g. Calculate the 95% CI. Mean -1. 96 x 528/ 1513 to Mean +1. 96 x 528/ 1513 3298 to 3352 11

CI FOR A PROPORTION SE(p)= p (1 -p)/n 95% CI= ± 1. 96 x SE (p) 12
- Slides: 12