BIOS 501 Lecture 11 Comparing proportions Roderick Little

BIOS 501 Lecture 11 Comparing proportions Roderick Little UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Comparing Two Proportions o o tests of significance for difference in proportions confidence intervals for difference in proportions relative risk, odds ratio Book Section 8. 2 UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Example: Cardiac Arrhythmia Trial “RESULTS. CAST-II was stopped early because the first 14 -day period of treatment with moricizine after a myocardial infarction was associated with excess mortality (17 of 665 patients died or had cardiac arrests), as compared with no treatment or placebo (3 of 660 patients died or had cardiac arrests)” “was associated with excess mortality” because the Null Hypothesis of no association -- that is, that mortality rates are same in the two groups – is rejected We describe here the statistical analysis that underlies this statement UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH
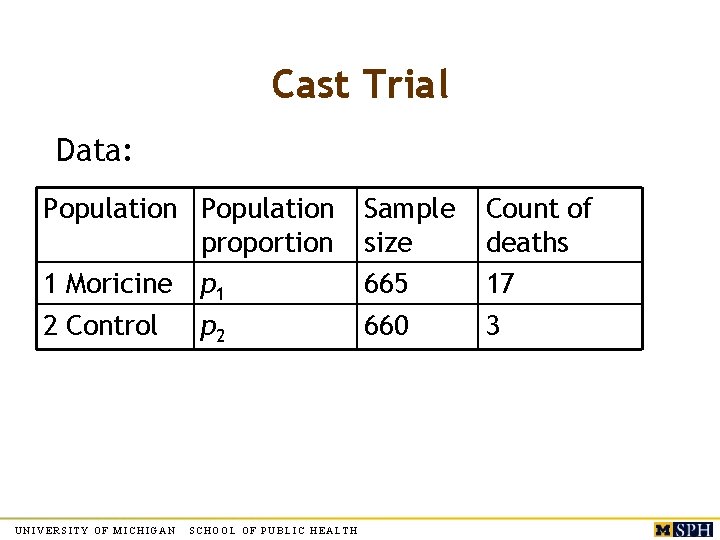
Cast Trial Data: Population proportion 1 Moricine p 1 2 Control p 2 UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH Sample size 665 660 Count of deaths 17 3

o o Example: Can warfarin be continued during dental extraction? Results of a randomized controlled trial SUMMARY. …Of 109 patients who completed the trial, 52 were allocated to the control group (warfarin stopped 2 days before extraction) and 57 patients were allocated to the intervention group (warfarin continued). The incidence of bleeding complications in the intervention group was higher (15/57, 26%) than in the control group (7/52, 14%)… but this difference was not significant… we found no evidence of an increase in clinically important bleeding. We will compute a test and confidence interval for difference in complication rate UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Warfarin Trial Data: Population 1 Warfarin 2 Control UNIVERSITY OF MICHIGAN Population proportion p 1 p 2 SCHOOL OF PUBLIC HEALTH Sample size 57 52 Count of complications 15 7

Comparing Two Proportions o General Notation: Population proportion 1 p 1 2 p 2 UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH Sample size n 1 n 2 Count of successes X 1 X 2

Independent groups design o o o Assume a simple random sample of size n 1 from a large population having proportion p 1 of successes and independent SRS of size n 2 from another large population having proportion p 2 of successes. is an estimator of p 1 is an estimator of p 2: UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Comparing Two Proportions: properties of estimators To compare p 1 and p 2, construct inferences for p 1 – p 2. UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Comparing Two Proportions: approximate normality is approximately normal o o Tests, confidence intervals are obtained using approx. standard normal variable UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Significance Test – Comparing Two Population Proportions o o When p 1 and p 2 are unknown, we test the null hypothesis H 0: p 1 = p 2 (same as H 0: p 1 -p 2=0) against one of the following alternatives: n H a : p 1 > p 2 n H a : p 1 < p 2 n H a : p 1 ≠ p 2 UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Comparing Two Population Proportions: Significance Test o Under the null hypothesis H 0: p 1 = p 2, we view all the data as coming from a single population with proportion p 1=p 2=p (p unknown). The z-statistic becomes o Since p is unknown, we use the pooled sample proportion to estimate it: UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Comparing Two Population Proportions. Significance Test o Null hypothesis: H 0: p 1 = p 2 o The test statistic is: Alternative Hypothesis H a : p 1 > p 2 H a : p 1 < p 2 H a : p 1 ≠ p 2 UNIVERSITY OF MICHIGAN P-value P(Z ≥ z) P(Z ≤ z) 2*P(Z ≥ | z |) SCHOOL OF PUBLIC HEALTH

Cast Trial Solution: UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Warfarin trial solution UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Confidence Interval for Difference in Two Population Proportions o o o We can also construct a confidence interval for p 1 – p 2. We again use to estimate the difference in population proportions. The estimated SE is n Note: this differs slightly from the SE for the null hypothesis, which pools the proportions UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Confidence Interval for p 1 – p 2 o A 95% confidence interval for p 1 – p 2 is given by o Use this interval when each sample has at least 5 successes and 5 failures. n n 90% CI, replace 1. 96 by 1. 645, 99% CI, replace 1. 96 by 2. 576, etc. UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Example (CAST Trial): o Estimate with 95% confidence the difference in mortality rates in the two treatment arms. UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Example (Warfarin Trial): o Estimate with 99% confidence the difference in complication rates in the two treatment arms. UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Other measures for comparing proportions UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

What about paired data? o o o D = difference in outcomes within each pair (possible values -1, 0, 1) Large samples: treat differences like a normal sample. E. g. 95% CI is Small samples: discard ties (where difference = 0), define 1 as “success”, -1 as “failure” and analysis proportion of successes (Mc. Nemar test) UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH

Summary o o Confidence intervals and tests for comparing proportions Normal approximation: OK with at least 5 successes, 5 failures in each group Plus four correction for small samples: add 1 success, 1 failure to each sample Relative risk, odds ratio UNIVERSITY OF MICHIGAN SCHOOL OF PUBLIC HEALTH
- Slides: 22