Biomedical Signal Processing Forum August 30 th 2005

Biomedical Signal Processing Forum, August 30 th 2005

Bio. Sens (2/2) : wavelet based morphological ECG analysis Joel Karel, Ralf Peeters, Ronald L. Westra Maastricht University Department of Mathematics Biomedical Signal Processing Forum, August 30 th 2005

Biosens: prehistory from 1994 onwards TU Delft micro electronics UM mathematics Richard Houben Medtronic Bakken Research Maastricht Other companies UM Fysiology Prof. M. Allessie

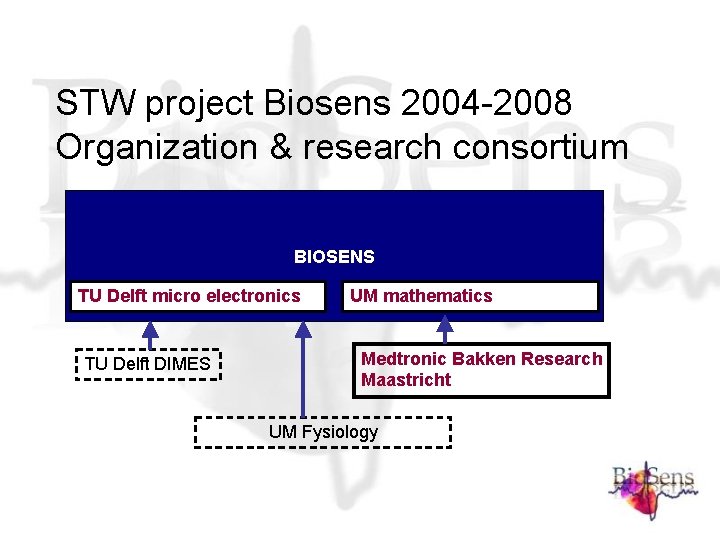
STW project Biosens 2004 -2008 Organization & research consortium BIOSENS TU Delft micro electronics TU Delft DIMES UM mathematics Medtronic Bakken Research Maastricht UM Fysiology

Research topics studied so far 1. Efficient analog implementation of wavelets • Analog implementation of wavelets allows low-power consuming wavelet transforms for e. g. implantable devices • Wavelets cannot be implemented in analog circuits directly but need to be approximated: A good approximation approach will allow reliable wavelet transforms Focus on: morphological analysis 2. Epoch detection and segmentation • Application of the Wavelet Transform Modulus Maxima method to T-wave detection in cardiac signals. 3. Optimal discrete wavelet design for cardiac signal processing • What is the best wavelet relative to the data and pupose?

1. Efficient implementation of analog wavelets Biosens team: J. M. H. Karel (Ph. D-student), dr. R. L. M. Peeters, dr. R. L. Westra Accepted papers: BMSC 2005 (Houffalize, Belgium), IFAC 2005 (Prague, Czech Republic), and CDC/EDC 2005 (Sevilla, Spain)

Implementation of wavelets • Analog implementation of wavelets allows low-power consuming wavelet transforms for e. g. implantable devices • Wavelets cannot be implemented in analog circuits directly but need to be approximated

Wavelet approximation considerations • A good approximation approach will allow reliable wavelet transforms • will allow low-order implementation (low-power consuming) of wavelet transforms • allows approximation of various types of wavelets • is relatively easy applicable

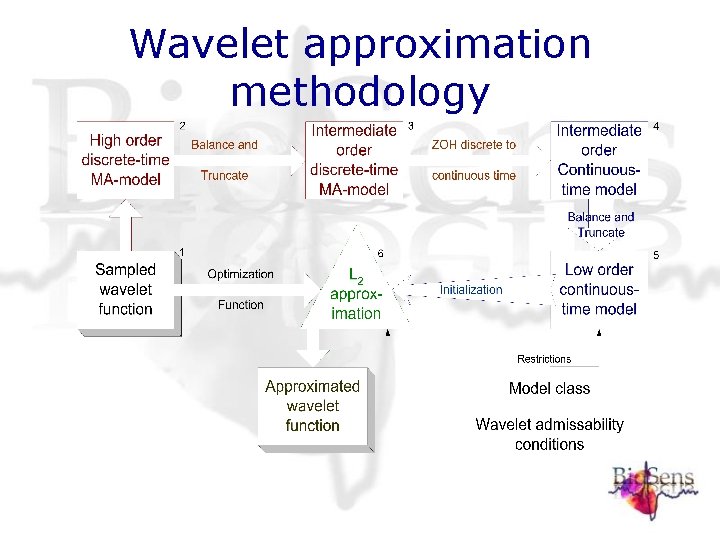
Wavelet approximation methodology

Initial high-order discrete time MA-system • Sampled wavelet function • Required i. r. • State-space realization in controllable companion form

Model reduction with balance and truncate • Balance Lyapunov-equations • Note that P is identity matrix • Reduce system based on Hankel singular values

L 2 -approach • Wavelet is approximated by impulse response of system • The model class is determined by the system who’s i. r. is used as a starting point

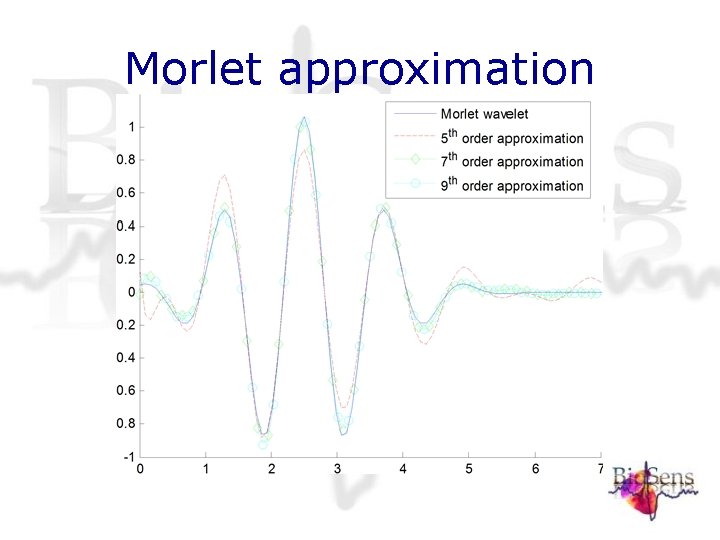
Morlet approximation

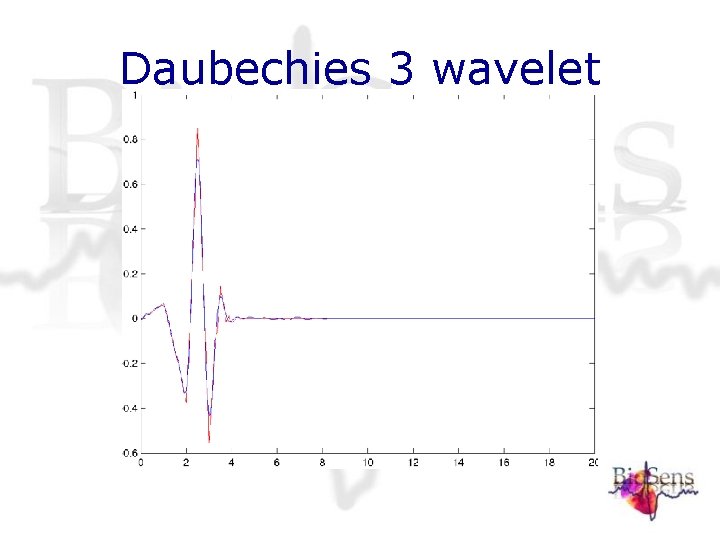
Daubechies 3 wavelet

Wavelet approximation methodology • Allows approximation of wavelet function that previously could not be approximated • Allows approximation of more generic functions • Publications accepted for: IFAC 2005 (Prague, Czech Republic), CDC/ECC 2005 (Sevilla, Spain), and BMSC 2005 (Houffalize, Belgium),

2. ECG morphological analysis using designer wavelets Biosens team: J. M. H. Karel (Ph. D-student), dr. R. L. M. Peeters, dr. R. L. Westra Graduation students: Pieter Jouck, Kurt Moermans, Maarten Vaessen

Wavelet based signal analysis Signal Data Analyzing wavelet Purpose of application

Signal morphology and optimal wavelet design (1) • Design wavelet such that they detect morphology in signal • Wavelet transform can be seen as convolution • Maximum values if wavelet resembles signal in an L 2 sense • Fit a wavelet to signal or create optimal wavelet in wavelet domain

Signal morphology and optimal wavelet design (2) • Can be used to detect epochs • Detecting morphologies related to pathologies • Computational efficient

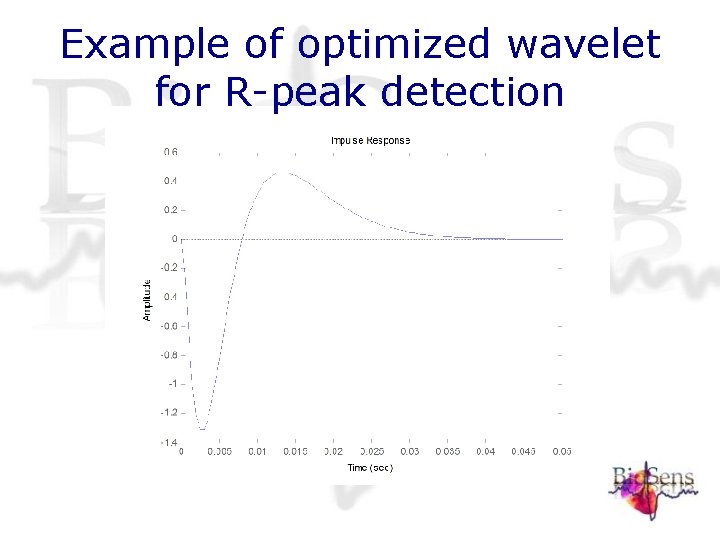
Example of optimized wavelet for R-peak detection

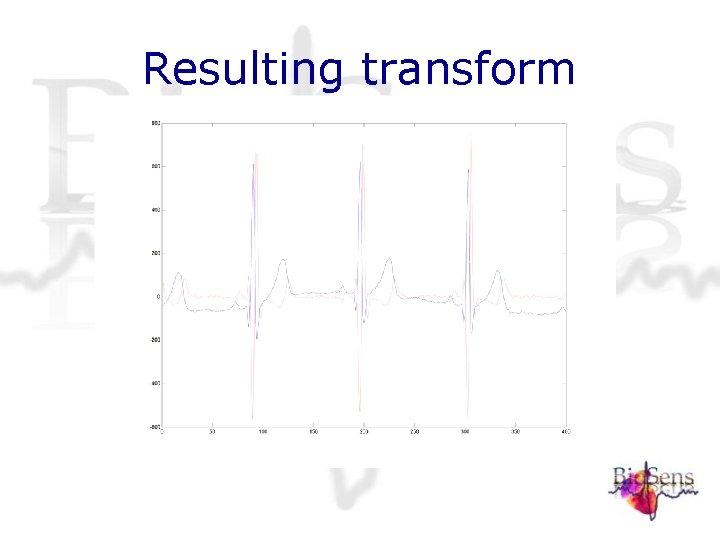
Resulting transform

2. 1 Application of the wavelet Transform Modulus Maxima method to T-wave detection in cardiac signals J. M. H. Karel, P. Jouck, R. L. Westra

T-wave detection in electrocardiograms • Pilot study based on state-of-the-art approach (e. g. Li 1995, Butelli 2002) • WTMM-based algorithm • Approximation of singular value (Lipschitz coefficient) did not show to be particularly discriminating • Approach successful on a variety of R&T-wave morphologies • Classification strategy rather ad hoc

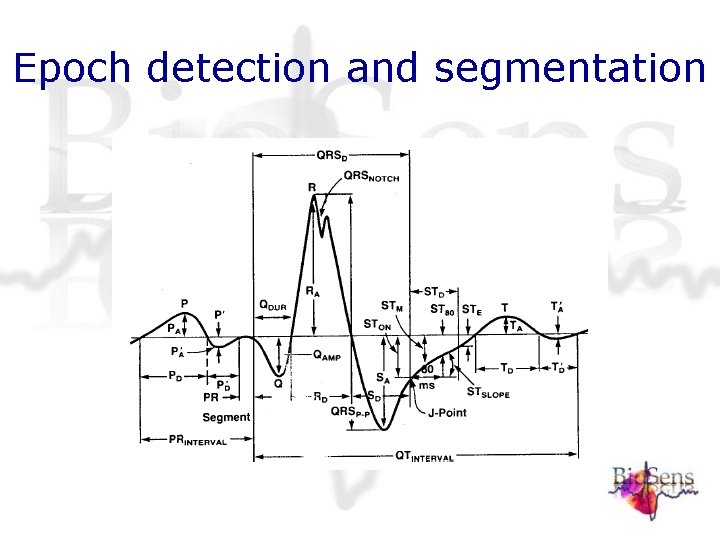
Epoch detection and segmentation

Example: Application of the Wavelet Transform Modulus Maxima method to T-wave detection in cardiac signals

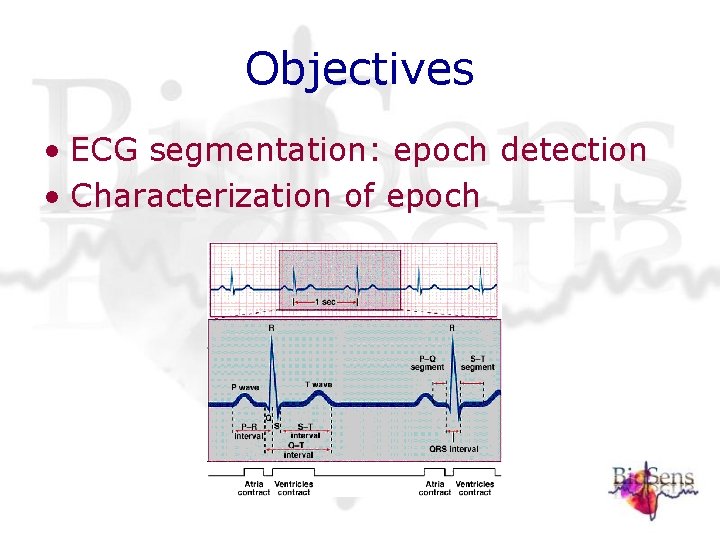
Objectives • ECG segmentation: epoch detection • Characterization of epoch

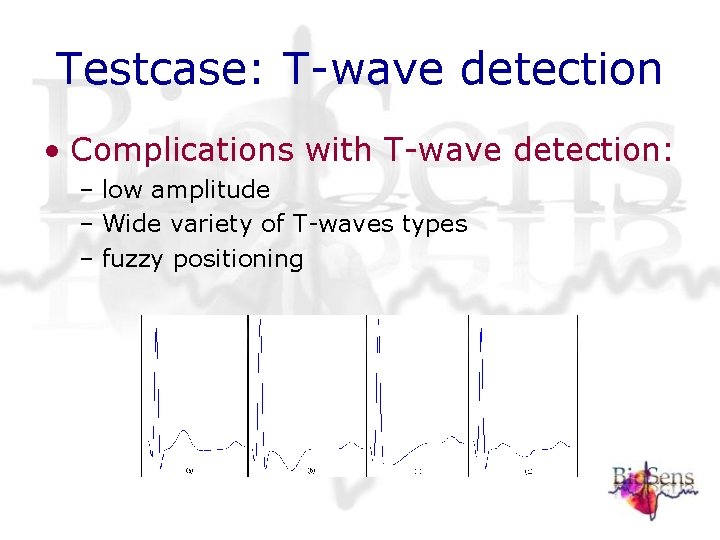
Testcase: T-wave detection • Complications with T-wave detection: – low amplitude – Wide variety of T-waves types – fuzzy positioning

Conventional Methodes • 1 st step : Filter → filtering of fluctuations and artifacts • Different types of filters – Differential filters – Digital filters • 2 d step : Signal comparsion using threshold

Conventional Methods • Advantages: – Simple and straightforward methodology – Ease of implementation • Disadvantages: – Sensitive for stochastic fluctuations – Bad detection of complexes with low amplitudes

Wavelet Transform • Wavelet transform of signal f using wavelet : – Frequency and time domain – Spectral analysis by scaling with a (dilation) – Temporal analysis by translation with b

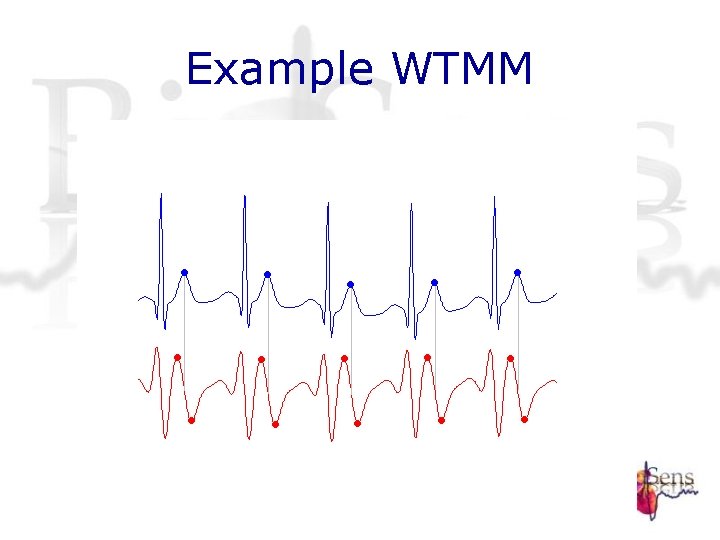
Example WTMM

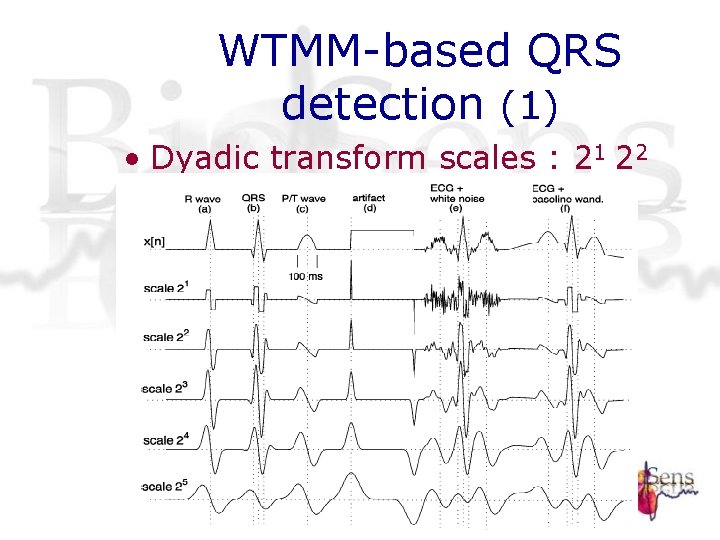
WTMM-based QRS detection (1) • Dyadic transform scales : 21 22 23 24

WTMM-based QRS detection (2) • Identification of Modulus Maxima – QRS-complex → 2 modulus maxima (MM) – Find all MM on all scales • Delete redundant MMs – 2 positive or 2 negative recurring MMs – Proximate MM multiples (too close for comfort)

WTMM-based QRS detection (3) • Positioning of R-peak – Zero-crossing between positive and negative MMs

Adjustments for T-wave detection • Transform to scale 10

Adjustments for T-wave detection • Search for Modulus Maxima – Only MMs above a given threshold • Position of T-wave peak – Normal T-wave → MM pare → zero-crossing – T-wave with single increase/decrease → one MM near peak

Results • Sensitivity of WTMM-based methode to: – Low T-wave amplitudes – Noise and stochastic variation – Baseline-drift – complex T-wave morphology

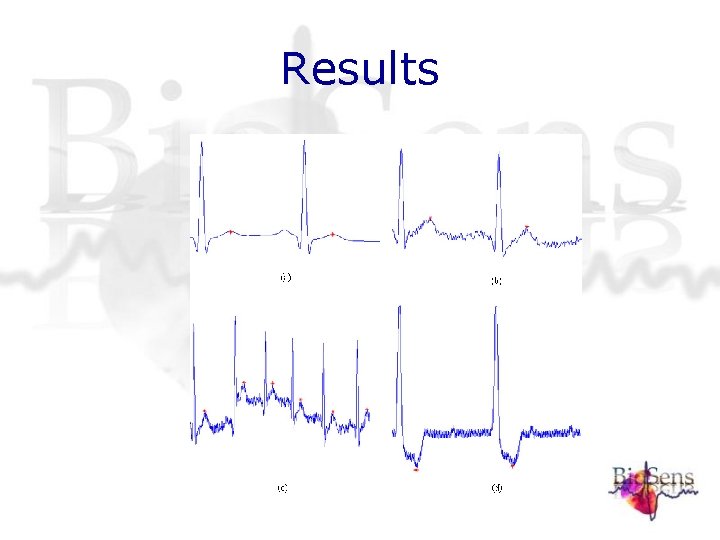
Results

Results • Testcases: Signals from: i) MIT-BIH database, and ii) Cardiology department of Maastricht University. • Performance: • • Number of True Positive detections (True. Pos) Number of False Positive detections (False. Pos) Number of True Negative detections (True. Neg) Number of False Negative detections (False. Neg) Total number of peaks (Total. Peak) Percentage of detected T-waves (Sensitivity) Percentage of correct detections (Perc. Corr)

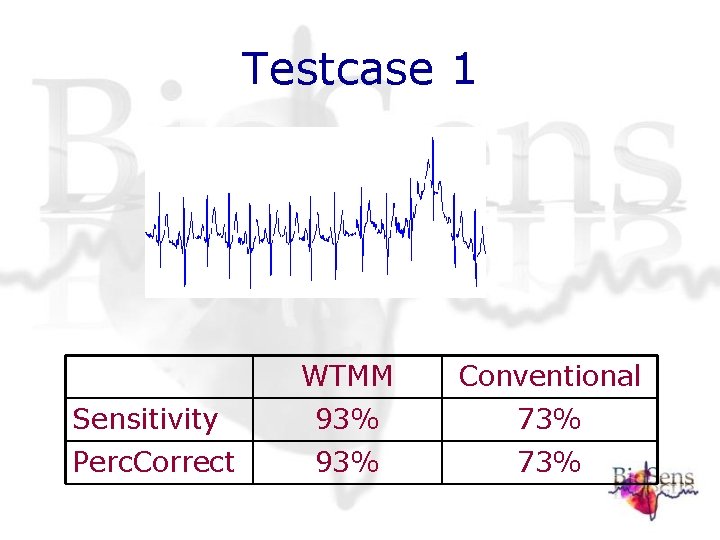
Testcase 1 WTMM Conventional Sensitivity 93% 73% Perc. Correct 93% 73%

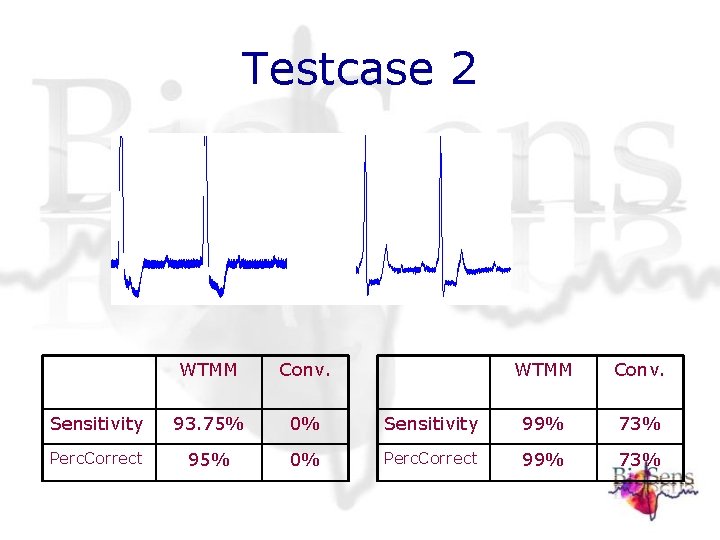
Testcase 2 WTMM Conv. Sensitivity 93. 75% 0% Perc. Correct 95% 0% WTMM Conv. Sensitivity 99% 73% Perc. Correct 99% 73%

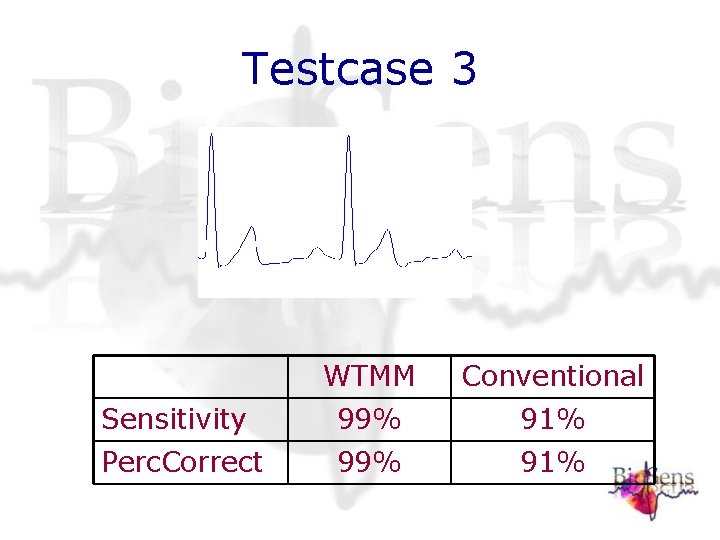
Testcase 3 WTMM Conventional Sensitivity 99% 91% Perc. Correct 99% 91%

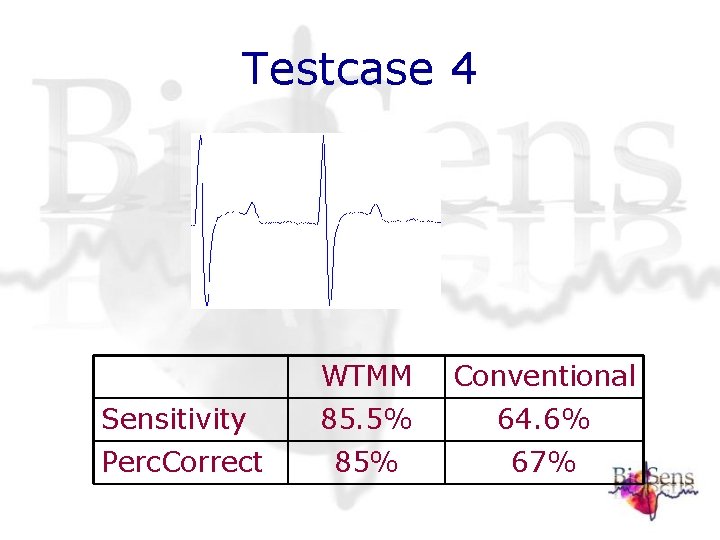
Testcase 4 WTMM Conventional Sensitivity 85. 5% 64. 6% Perc. Correct 85% 67%

Discussion • Problems – Low amplitude + high noise levels – Extremely short ST-intervals – Not all types of T-wave are detected • Improvements – Automatic scale adjuster – More decision rules – Learning algorithm

Conclusion • Reliable method • Robust and noise-resistent • Good performance in sense of sensitivity and percentage correct (typically > 85%)

2. 2 Optimal discrete wavelet design for cardiac signal processing J. M. H. Karel, R. L. M. Peeters and R. L. Westra EMBC 2005(= 27 th Annual International Conference of the IEEE Engineering in. Medicine and. Biology Society ), 1 -4 September 2005, Shanghai, People’s Republic of China

Optimal Wavelet Design What is a good wavelet for a given signal and a given purpose? • Freedom in choice for analyzing wavelet (t) • Best output (= wavelet coefficients ck) are well positioned in frequency-temporal space, i. e. sparse representation • Essentials: perfect reconstruction, orthogonal waveletmulti resolution structure, vanishing moments of wavelets, flatness of filter, smooth wavelets • Measure the performance of a given signal x(t) and a trial wavelet (t) with a criterion function V[ ]

Optimal Wavelet Design Orthogonal wavelets and filter banks

Wavelet analysis and synthesis • Low pass filter with transfer function C(z) • High pass filter with transfer function D(z) • Combination with down-sampling • has compact support C, D are FIR

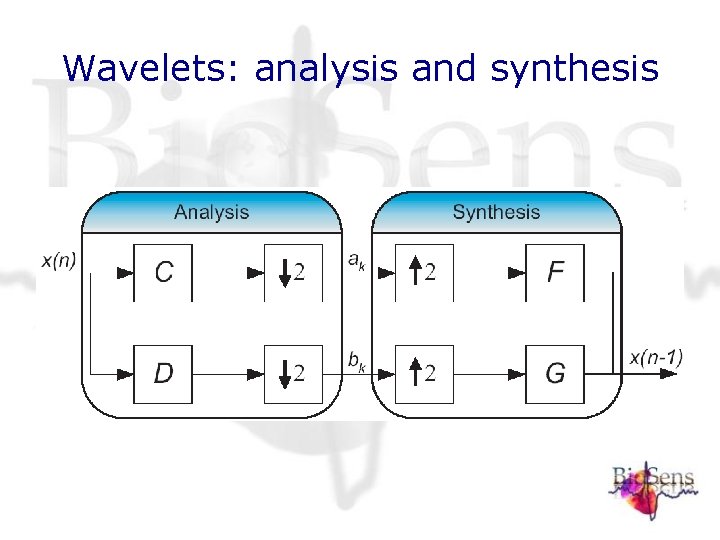
Wavelets: analysis and synthesis

Filter bank

Filter bank

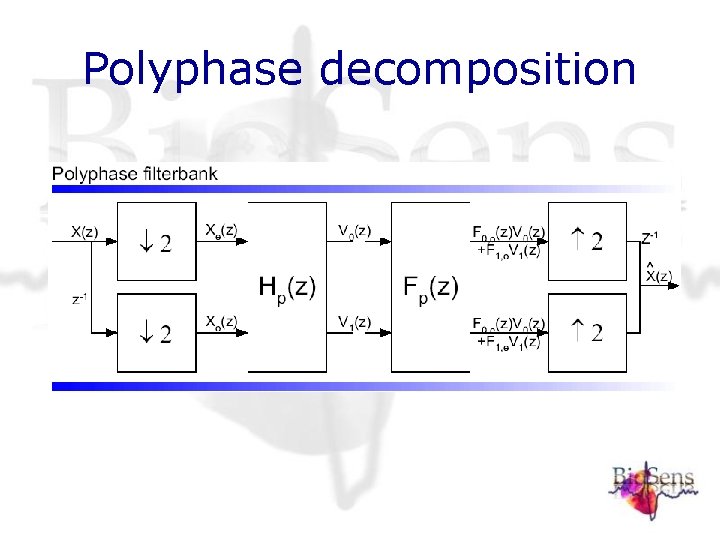
Polyphase decomposition

Polyphase decomposition the alternating flip construction relates coefficients c and d: the remaining orthogal freedom in the 2 n ck can be expressed by a reparametrization in n new parameters i: the polyphase matrices. R and

Polyphase decomposition The polyphase matrices R and Λ in terms of parameters θi are defined as: Then define the 2 x 2 matrix H as:

Polyphase decomposition Matrix H can be partitioned as: with:

Polyphase decomposition Now the matrices C and D can be written as:

Design criteria on the wavelet put constraints on C and D • The polyphase decomposition handles the orthogonalityof the filterbank • Another desirable property are the vanishing moments • This puts constraintson C and D, e. g. C(z) has zeros at: z + 1 = 0, ditto corresponding flatness of C and D at high/low frequencies • The condition of vanishing moments translates to a linear set of constraints on the filter coefficients c and d

Design criteria on the wavelet put constraints on C and D • For instance one vanishing moment states: • this translates to a constraint on c and d: • And so also to a constraint on the s:

Computing the wavelet and scaling function • The scaling function relates to the wavelet via the dilation equation. • Using the alternating flip construction this states:

Computing the wavelet and scaling function • The resulting functions and may be discontinuous and fractal • The dilation relation allows an iteration scheme for the coefficients:

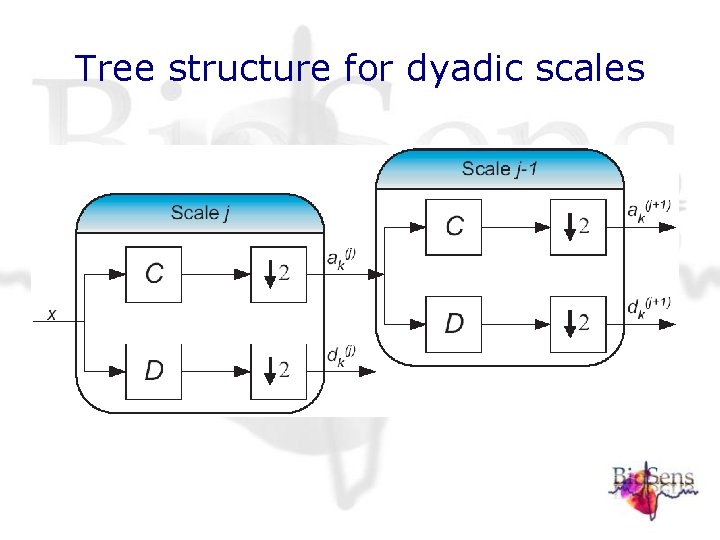
Tree structure for dyadic scales

Criteria to measure the quality of a wavelet for given data • The energy of the original signal x(t) is: • Because of the orthogonality this energy is preserved in the wavelet representation: • Therefore, the L 2 -norm is not a suitable criterion

Wavelet design criteria Philosophy and algorithm Guiding principle proposed here is to aim for maximization of the variance. This is achieved by either : • maximization of the variance of the absolute values of the wavelet coefficients minimization of 1 L-norm • maximization of the variance of the squared wavelet coefficients maximization of 4 L-norm

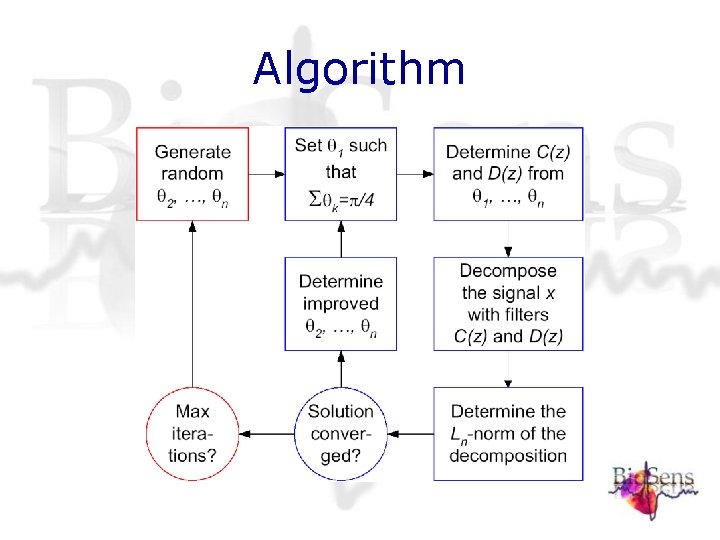
Algorithm

Wavelet Design Criteria Remarks • The criteria min L 1 and max L 4 have been investigated to design wavelets for various given signals. • When all wavelet coefficients are taken into account and no weightingis applied, both criteria tend to produce similar results. • However, when only a few scales are taken into account (e. g. by weighting) the results may become different: in case of minimization of the L 1 -norm energy tends to be placed in scales not taken into account , whereas in case of maximization of the L 4 -norm this does not happen.

Experimentation I. Reconstruction of artificially generated noisy signals • Make an artificial sparse signal x(t) by setting only a few wavelet-coefficients ck to non-zero values • Note that this signal probably has a small L 1 -norm (sparse) and a large L 4 -norm (large variance) • Add some white noise v(t) and apply the wavelet-design algorithm to this signal x(t) + v(t) • The reconstructed signal x*(t) fits perfectly with x(t) up to a signal-to-noise ratio (snr) 1

Experimentation II. Reconstruction of a reference signal • Reference signal x(t) is obtained by averaging comparable episodes from ECG signals from the MIT Physionet normal sinus rhythm database • Resulting smooth signal is upsampled:

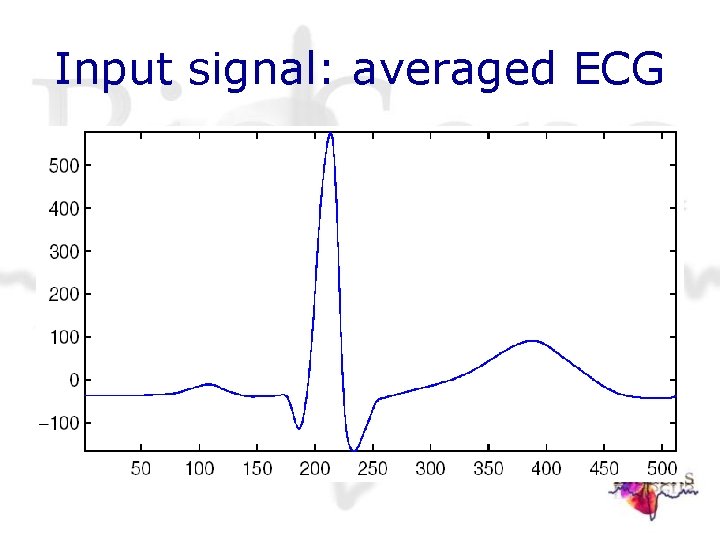
Input signal: averaged ECG

Experimentation Local optima in the -parameter space • Consider the situation with n=3, i. e. three s • Because: 1+ 2+ 3= /4 this situation has two degrees of freedom • Now we can plot the L 1 -criterion in the ( 2 , 3)-plane and study local optima:

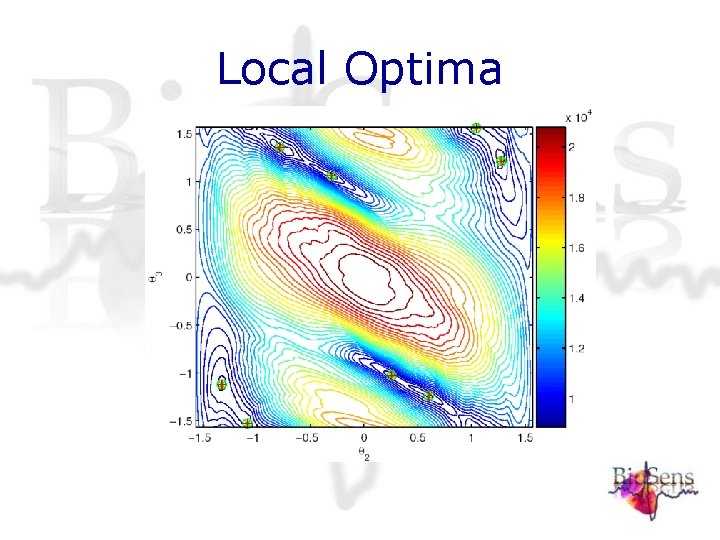
Local Optima

Experimentation Local optima in the -parameter space • The coefficients of the local optima closely resemble the Daubechies 2 filter coefficients • This observation gives a rationale for the use of th Daubechies 2 wavelet for cardiac signals • When the sum of 2 and 3 already is close to /4 only one degree of freedom is effectively used • some of the minor local optima resemble the Daubechies 3 wavelet, however to lesser extent

Experimentation The optimal number -parameters • The filter size of the wavelet filter is determined by the number n of s used • A large number of s gives freedom to fit the wavelet to the signal but also increases the complexity For n = 1 to 25 the L 1 -criterion averaged over 1000 random starting points is computed • • The graph is rather flat between n = 5 and n = 20, and n = 8 is a reasonable choice

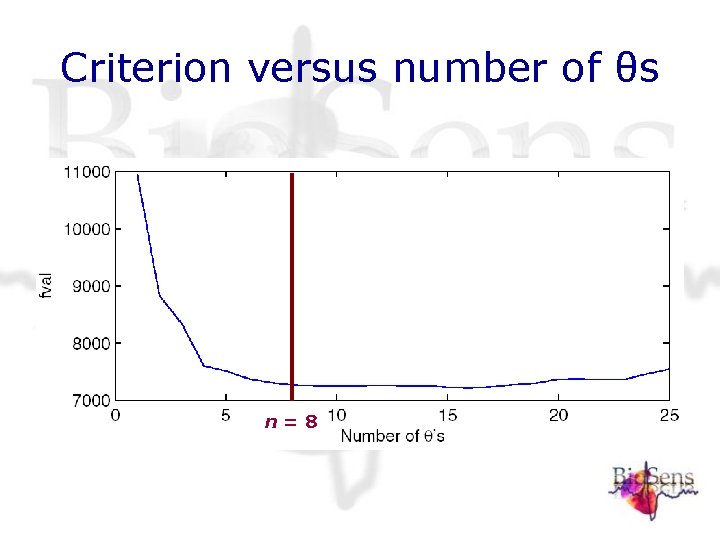
Criterion versus number of θs n=8

Experimentation Practical evaluation • Next we design the best fitting wavelet for the test set episode #103 of the MIT-BIH arrythmia database. This is a 360 Hz annotated ECG signal. • Two wavelets were designed using 8 θs by minimizing a criterion function V, with: 1. for 1 : V = L 1 -norm of the wavelet transform 2. for 2 : V = L 4 -norm of the wavelet transform

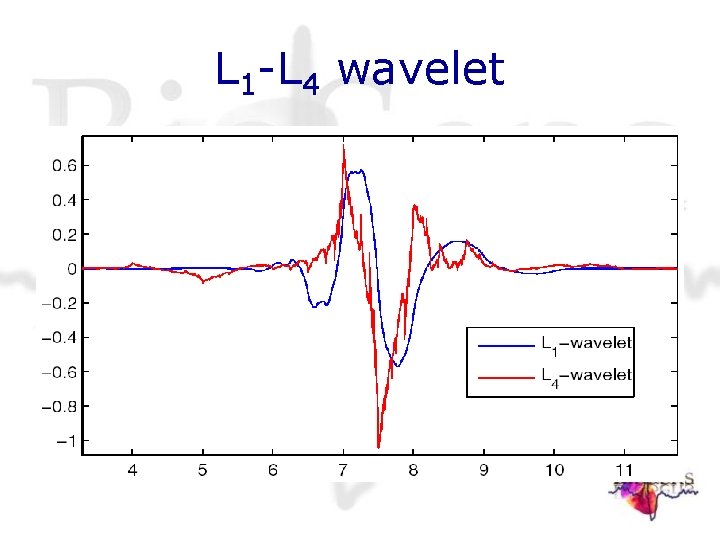
L 1 -L 4 wavelet

Experimentation Quality of the wavelet transform of the reference averaged ECG-signal with the L 4 -criterion maximized wavelet • • • The L 4 -wavelet has a fractal structure. The available degrees of freedom are not used to place poles at z = − 1 as with the Daubechies wavelets The fractal nature of the L 4 -wavelet is not relevant in processing, as only the coefficients are used in computations Moreover, the L 4 -wavelet is very effective in the wavelet decomposition of the reference signal. One single strong wavelet coefficient marks the location of largest correlation:

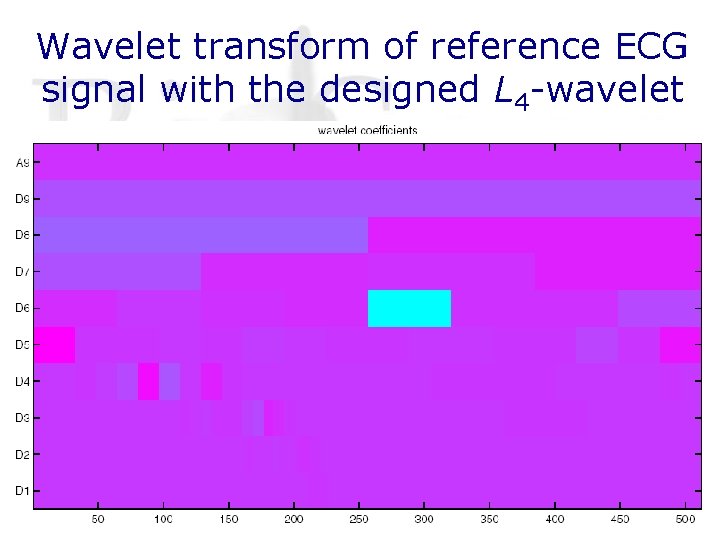
Wavelet transform of reference ECG signal with the designed L 4 -wavelet

Experimentation Comparison of the L 1 - and L 4 -wavelets with the Daubechies 2 wavelet • • The wavelet transform of the MIT-testset with was compared for the three wavelets (L 1, L 4, and Daubechies), on only a single level (scale) This level was selected for each wavelet individually to maximize performance A binary vector was constructed of all the wavelet coefficients of which the absolute value exceeded a certain threshold. These locations were related to the locations of the original signal The beat annotations in the testset were used as a reference to locate the QRS-complex.

Experimentation Comparison of the L 1 - and L 4 -wavelets with the Daubechies 2 wavelet • There are 1688 normal QRScomplexes in the MIT-testset. If the binary vector corresponding to the wavelet transform has detected a peak within 20 samples (56 ms) of the marker, it is assumed that the QRS-complex is detected. If a peak is detected but no marker is within 20 samples, a false detection is assumed • This comparison yielded the following results:

Results Comparison of the L 1 - and L 4 -wavelets with the Daubechies 2 wavelet

Conclusions Comparison of the L 1 - and L 4 -wavelets with the Daubechies 2 wavelet • The table shows that the performance of the Daubechies 2 wavelet is quite good • The L 4 optimized wavelet however shows superior performance • Furthermore the L 4 -wavelet is more robust with respect to the choice of threshold value, which may be a large advantage in practical applications

References [1] Gilbert Strang, Truong Nguyen, Wavelets and Filter Banks, Wellesley. Cambridge Press, 1996. [2] N. Neretti, N. Intrator, An adaptive approach to wavelet filter design, Proc. IEEE int. workshop on neural networks for signal processing, 2002. [3] A. L. Goldberger et al. . Physiobank, physiotoolkit, and physionet: Complex physiologic signals. Circulation, 101(23): e 215–e 220, June 2000. [4] Cuiwei Li et al. , Detection of ECG characteristic points using wavelet transforms. IEEE Transactions on Biomedical Engineering, 42(1): 21– 28, January 1995. [5] Stephane Mallat. A Wavelet Tour of Signal Processing. Ac. Press, 1999. [6] Ivo Provaznýk, Ji Kozumplýk. Wavelet transform in electrocardiography - data compression. International Journal of Medical Informatics, 45(12): 111– 128, June 1997. [7] M. P. Wachowiak et al. , Waveletbased noise removal for biomechanical signals: a comparative study. IEEE Transactions on Biomedical Engineering, 47(3): 360– 368, March 2000.

Focus for further research • Analysis of mathematical morphology of cardiac signals – Characterization of cardiac signals (clustering) – Expert input – Design of optimal multiwavelets • Development of online algorithm based on optimal wavelets and hardware implementation

Discussion Dr. Ronald L. Westra Department of Mathematics Maastricht University westra@math. unimaas. nl Biomedical Signal Processing Forum, August 30 th 2005