Biomedical Signal processing Chapter 4 Sampling of Continuous

Biomedical Signal processing Chapter 4 Sampling of Continuous Time Signals Zhongguo Liu Biomedical Engineering School of Control Science and Engineering, Shandong University 山� 省精品� 程《生物医学信号� 理(双� )》 http: //course. sdu. edu. cn/bdsp. html 2021/5/19 1 1 Zhongguo Liu_Biomedical Engineering_Shandong Univ.

Chapter 4: Sampling of Continuous Time Signals 4. 0 Introduction 4. 1 Periodic Sampling 4. 2 Frequency Domain Representation of Sampling 4. 3 Reconstruction of a Bandlimited Signal from its Samples 4. 4 Discrete Time Processing of Continuous Time signals 4. 5 Continuous time Processing of Discrete Time Signal 2

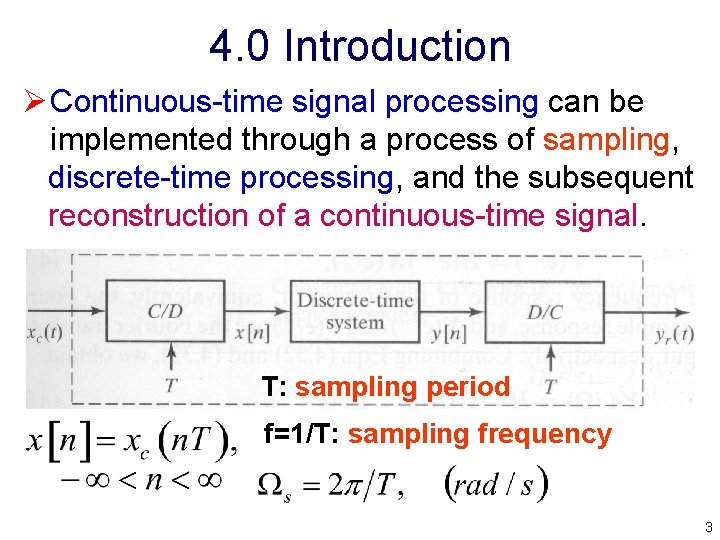
4. 0 Introduction Ø Continuous time signal processing can be implemented through a process of sampling, discrete time processing, and the subsequent reconstruction of a continuous time signal. T: sampling period f=1/T: sampling frequency 3

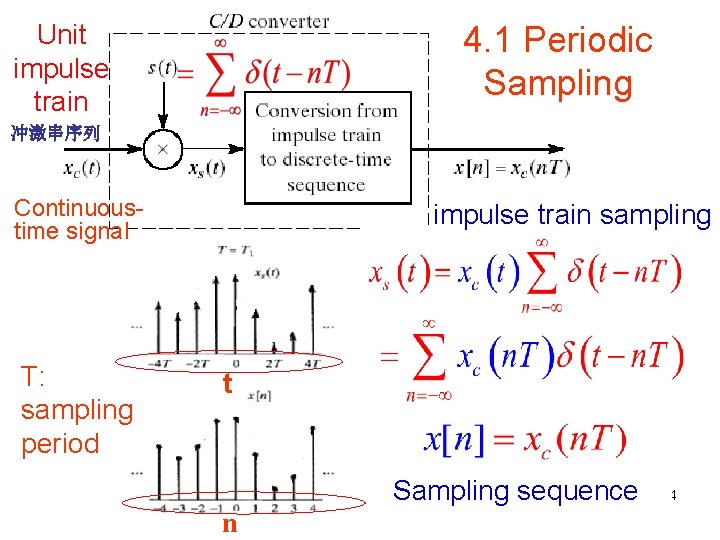
Unit impulse train 4. 1 Periodic Sampling 冲激串序列 Continuous time signal T: sampling period impulse train sampling t Sampling sequence n 4

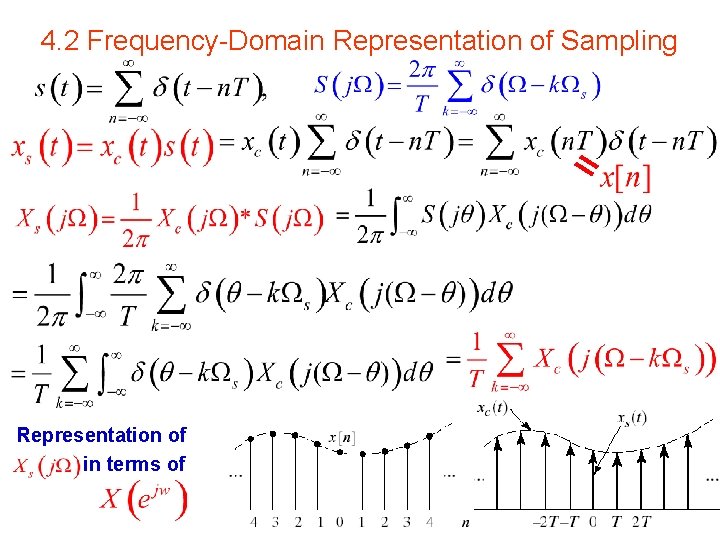
4. 2 Frequency Domain Representation of Sampling Representation of in terms of 7

Representation of in terms of , 数字角频率ω，rad 模拟角频率Ω, rad/s DTFT 采样角频率, rad/s 8

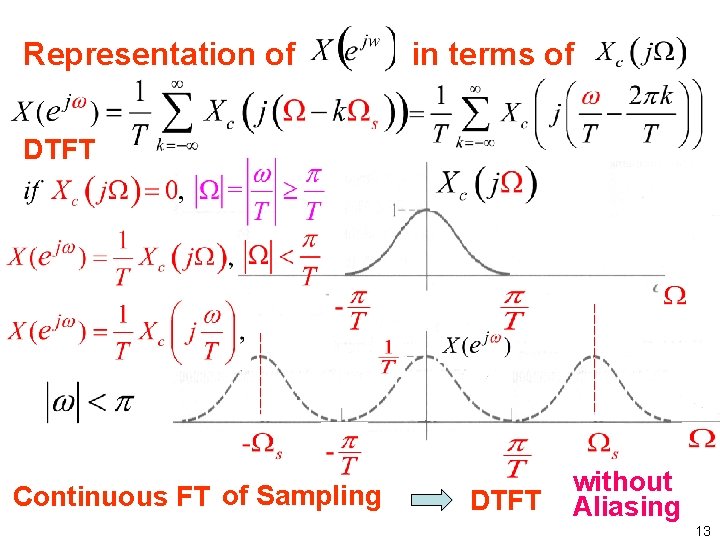
Representation of in terms of DTFT Continuous FT of Sampling DTFT without Aliasing 13

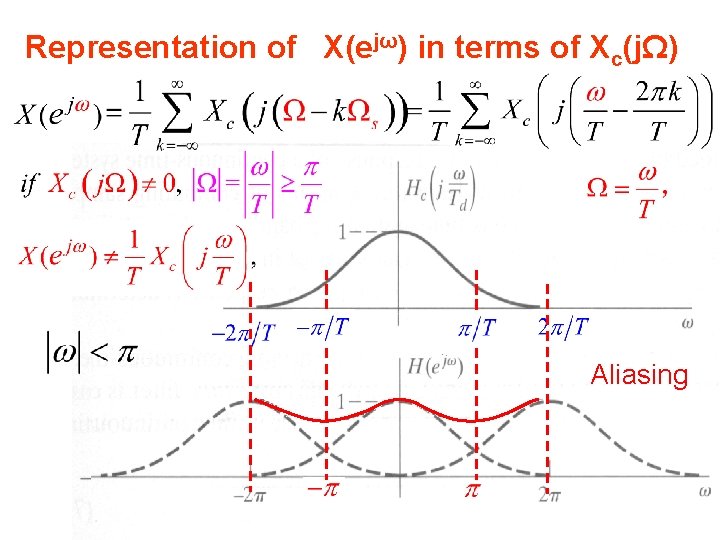
Representation of X(ejω) in terms of Xc(jΩ) Aliasing 15

Nyquist Sampling Theorem • Let be a bandlimited signal with is. Then uniquely determined by its samples , if . • The frequency is commonly referred as the Nyquist frequency. • The frequency is called the Nyquist rate, which is the minimum sampling rate (frequency). without Aliasing 17

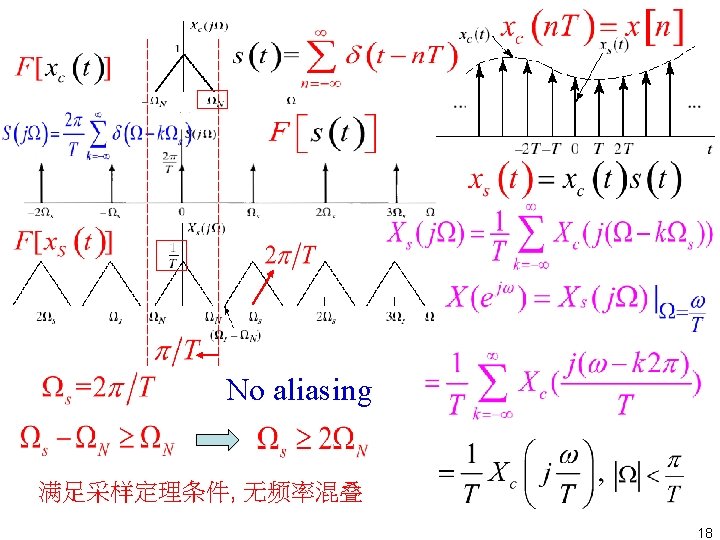
aliasing frequency 不满足采样定理条件 aliasing 19

Example 4. 1: Sampling and Reconstruction of a sinusoidal signal Compare the continuous-time and discrete-time FTs for sampled signal Solution: 21

Example 4. 1: Sampling and Reconstruction of a sinusoidal signal continuous-time FT of discrete-time FT of 22

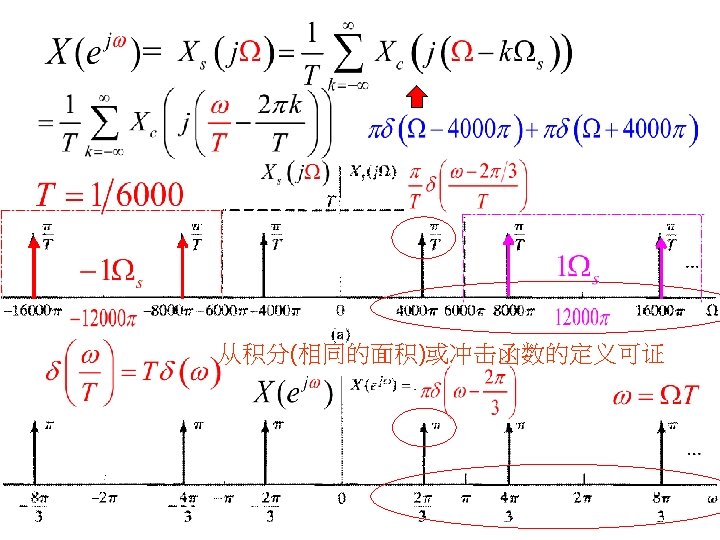
Ex. 4. 2: Aliasing in sampling an sinusoidal signal Compare the continuous-time and discrete-time FTs for sampled signal Solution: 24

Example 4. 2: Aliasing in the Reconstruction of an Undersampled sinusoidal signal continuous-time FT of discrete-time FT of 25

Ex. 4. 2: Aliasing in sampling an sinusoidal signal continuous-time FT of discrete-time FT of 低通滤波器 26

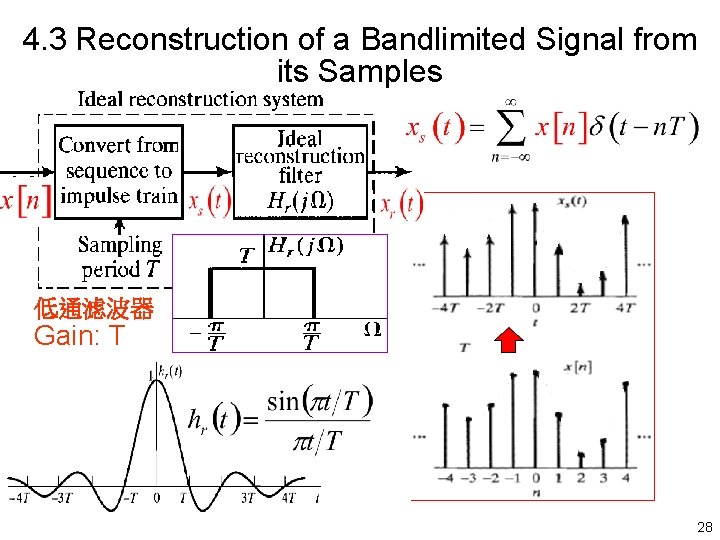
4. 3 Reconstruction of a Bandlimited Signal from its Samples 低通滤波器 Gain: T 28

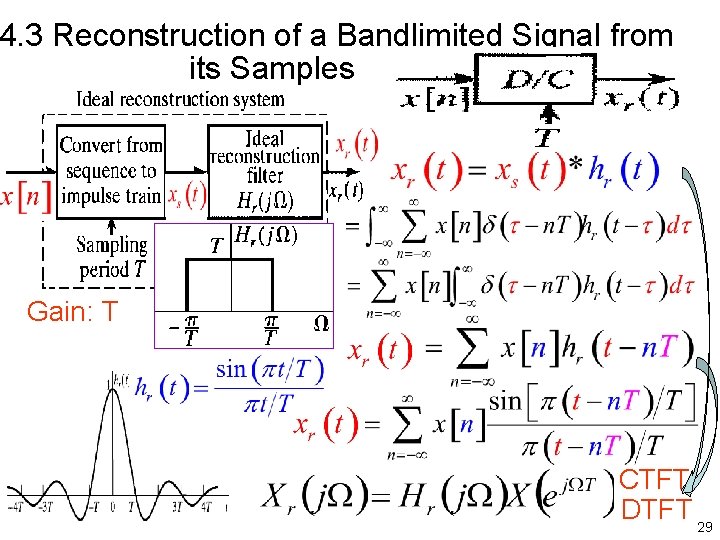
4. 3 Reconstruction of a Bandlimited Signal from its Samples Gain: T CTFT DTFT 29

4. 3 Reconstruction of a Bandlimited Signal from its Samples CTFT DTFT 只要满足Qs ≥ 2 QN 重建原信号 30

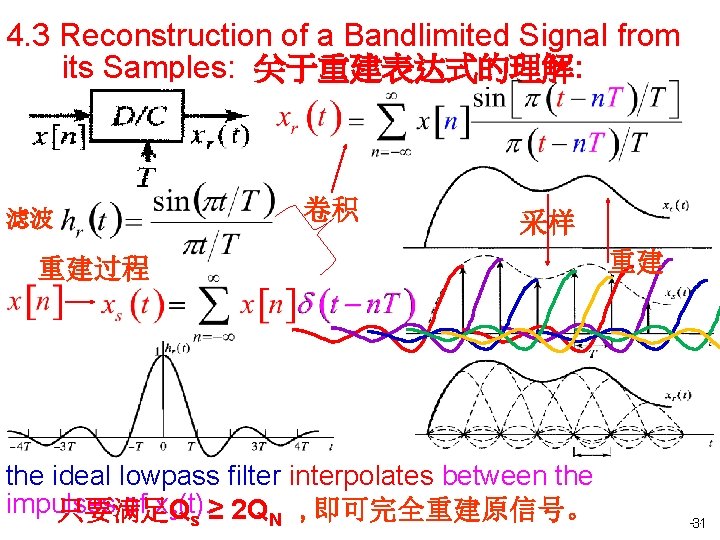
4. 3 Reconstruction of a Bandlimited Signal from its Samples: 关于重建表达式的理解: 滤波卷积采样重建过程 the ideal lowpass filter interpolates between the impulses of xs(t). 只要满足Q s ≥ 2 QN , 即可完全重建原信号。重建 31 31

4. 4 Discrete Time Processing of Continuous Time signals 32

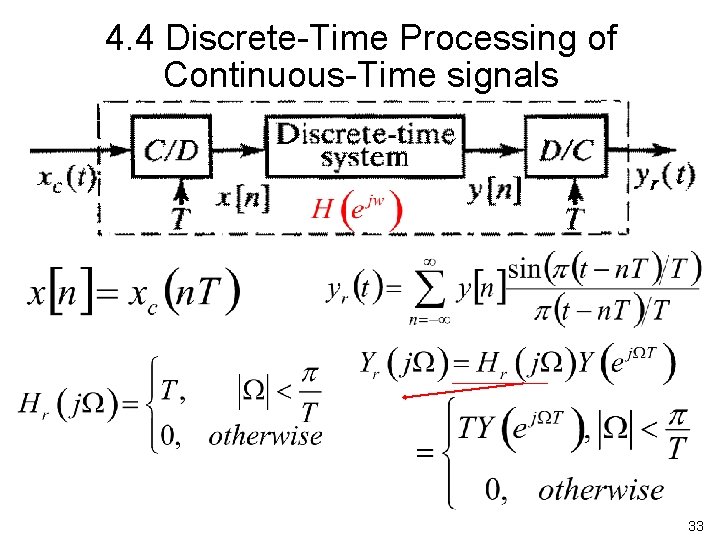
4. 4 Discrete Time Processing of Continuous Time signals 33

4. 4. 1 LTI DT Systems Is the system Linear Time. Invariant? 采样频率即采样时无频率混叠. 36

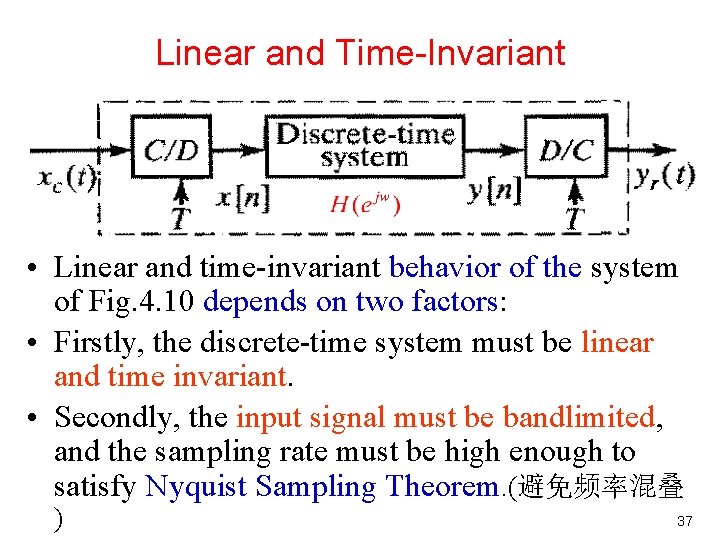
Linear and Time Invariant • Linear and time-invariant behavior of the system of Fig. 4. 10 depends on two factors: • Firstly, the discrete-time system must be linear and time invariant. • Secondly, the input signal must be bandlimited, and the sampling rate must be high enough to satisfy Nyquist Sampling Theorem. (避免频率混叠 ) 37

等效的连续时间系统必须是带限的. This is the effective frequency response of the overall LTI continuous time system. 38

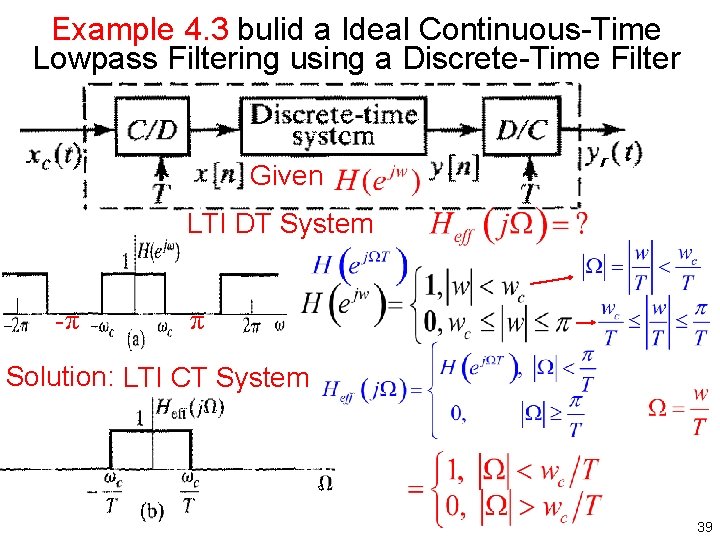
Example 4. 3 bulid a Ideal Continuous Time Lowpass Filtering using a Discrete Time Filter Given LTI DT System -π π Solution: LTI CT System 39

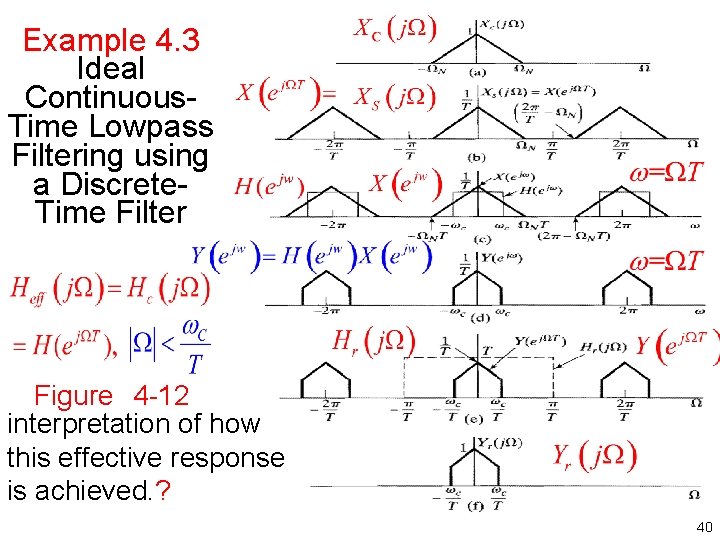
Example 4. 3 Ideal Continuous Time Lowpass Filtering using a Discrete Time Filter Figure 4 12 interpretation of how this effective response is achieved. ? 40

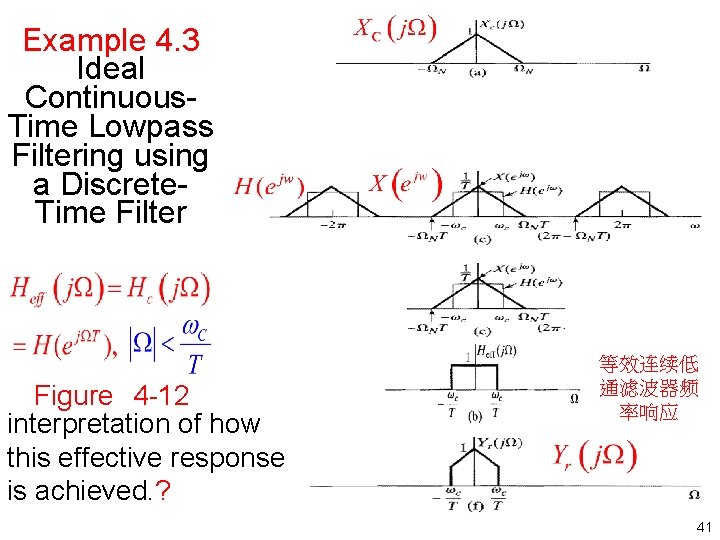
Example 4. 3 Ideal Continuous Time Lowpass Filtering using a Discrete Time Filter Figure 4 12 interpretation of how this effective response is achieved. ? 等效连续低通滤波器频率响应 41

Example 4. 4: Discrete Time Implementation of an Ideal Continuous Time Bandlimited Differentiator If inputs are bandlimited, Solution: Differentiator: • Frequency response: • The inputs are restricted to be bandlimited. • For bandlimited signals, it is sufficient that: 高于π/T的频率响应也用不到. has frequency • The corresponding DT system response: 42

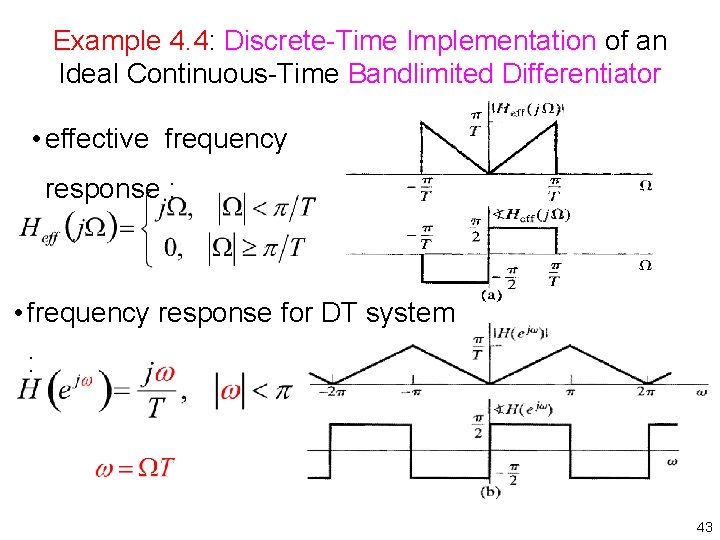
Example 4. 4: Discrete Time Implementation of an Ideal Continuous Time Bandlimited Differentiator • effective frequency response : • frequency response for DT system : 43

Example 4. 4: Discrete Time Implementation of an Ideal Continuous Time Bandlimited Differentiator • frequency response for DT system : • The corresponding impulse response : • or equivalently, 44

4. 4. 2 Impulse Invariance Given: Design: 关系？ impulse-invariant version of the 脉冲响应不变型 continuous time system 45

4. 4. 2 Impulse Invariance Ø Two constraints 脉冲响应不变法 1. 这是前面推出的结果要求 2. hc(t) is bandlimited 且与采样频率关系？截止频率采样不产生频率混叠脉冲响应不变型 The discrete-time system is called an impulse-invariant version of the continuous time system. If Let 46

Example 4. 5: A Discrete Time Lowpass Filter Obtained by Impulse Invariance • Suppose that we wish to obtain an ideal lowpass discrete time filter with cutoff fre quencyω c < π , • by sampling a continuous time ideal lowpass filter with cutoff frequency /T Nyquist Ω frequency Ωc <π采样频率/2 c = ωc /T< 满足采样定理条件 defined by : find Solution: • The impulse response of CT system : 47

Example 4. 5: A Discrete Time Lowpass Filter Obtained by Impulse Invariance • The impulse response of CT system : • so define the impulse response of DT system to be: check the frequency response • The DTFT of this sequence : Ωc = ωc /T< π /T 满足采样定理条件, 无频率混叠 48

Example 4. 6: Impulse Invariance Applied to Continuous Time Systems with Rational System Functions • Many CT systems have impulse responses of 频带 form: 无限 • Its Laplace transform: • apply impulse invariance concept to CT system, we obtain the h[n] of DT system: 不满足采样定理条件 • which has z transform system function: 49

Example 4. 6: Impulse Invariance Applied to CT Systems with Rational System Functions • CT system have impulse responses of form: L • Sampling: • z transform : • assuming Re(s 0) < 0, the frequency response: 单位圆在收敛域存在FT 不满足采样定理条件, 存在频率混叠但对高阶系统, 频率混叠可忽略, 所以脉冲响应不变法可用于设计滤 50 波器。

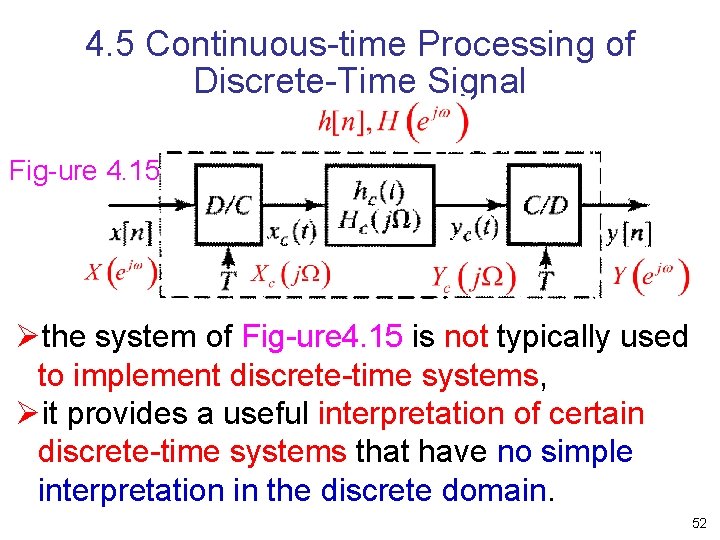
4. 5 Continuous time Processing of Discrete Time Signal Fig ure 4. 15 Øthe system of Fig ure 4. 15 is not typically used to implement discrete time systems, Øit provides a useful interpretation of certain discrete time systems that have no simple interpretation in the discrete domain. 52

4. 5 Continuous time Processing of Discrete Time Signal Sampling without aliasing 54

4. 5 Continuous time Processing of Discrete Time Signal 55

Example 4. 7: Non integer Delay • The frequency response of a discrete time system • When is integer, integer Δ • When (=0. 5) is not an integer, it has no formal meaning we cannot shift the sequence x[n] by. interpreted by system 如何理解？ • (=0. 5) It can be 56

Example 4. 7: Non integer Delay Let • It represents a time delay of • and 对连续时间系统 T seconds. Therefore, 输出y[n]是将x[n]先变换成xc(t), 将其延迟ΔT (0. 5 T)时刻之后再采样得到的离散时间序列. 57

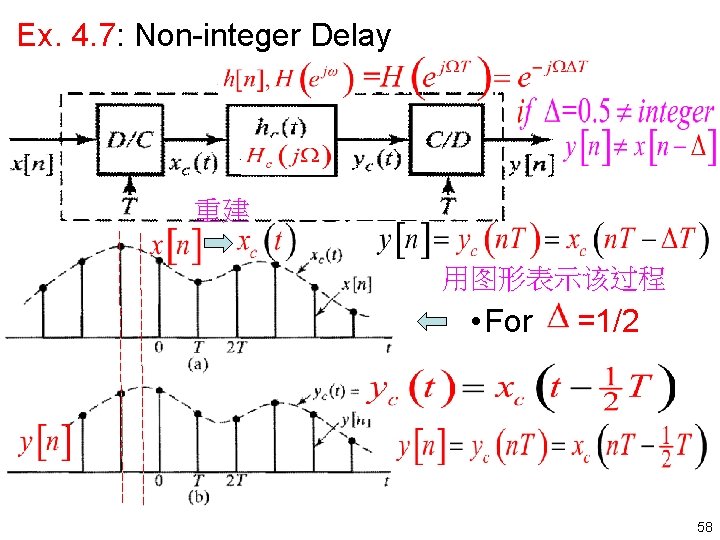
Ex. 4. 7: Non integer Delay 重建用图形表示该过程 • For =1/2 58

Example 4. 7: Non integer Delay for LTI system, proof? DTFT • When = n 0 is integer, 59

Review u What is Nyquist rate？ u What is Nyquist frequency？ u The Nyquist rate is two times the bandwidth of max frequency a bandlimited signal. u The Nyquist frequency is one half the Nyquist rate. u (The Nyquist frequency is half the sampling minimum Sampling without aliasing frequency. ) 61

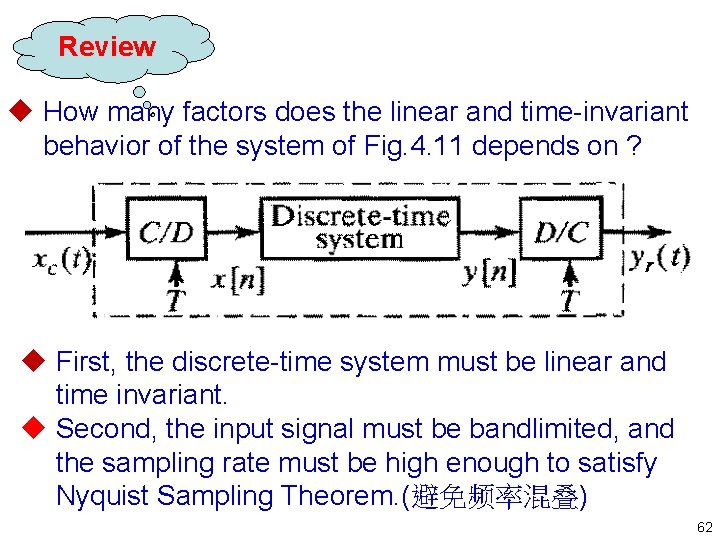
Review u How many factors does the linear and time invariant behavior of the system of Fig. 4. 11 depends on ? u First, the discrete time system must be linear and time invariant. u Second, the input signal must be bandlimited, and the sampling rate must be high enough to satisfy Nyquist Sampling Theorem. (避免频率混叠) 62

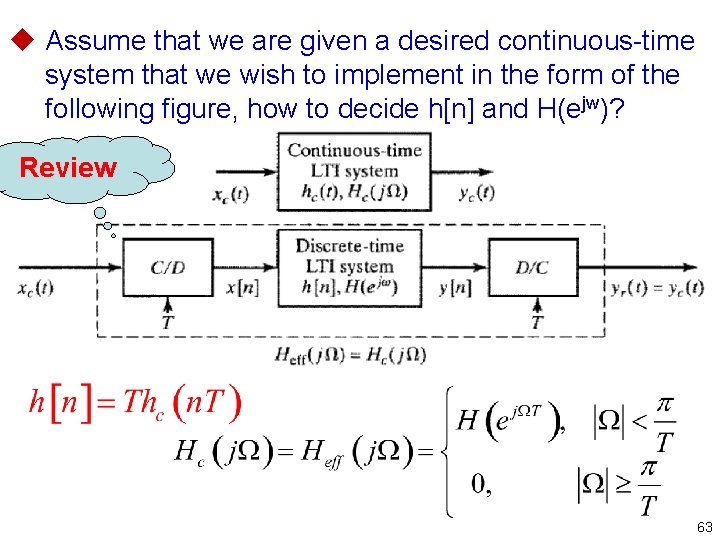
u Assume that we are given a desired continuous time system that we wish to implement in the form of the following figure, how to decide h[n] and H(ejw)? Review 63

Chapter 4 HW • 4. 5 2021/5/19 64 返回上一页下一页 Zhongguo Liu_Biomedical Engineering_Shandong Univ.