Biomedical Electronics Bioinstrumentation Introduction to Analogue Filters Contents

Biomedical Electronics & Bioinstrumentation Introduction to Analogue Filters

Contents Why use Analogue Filters? Types of Filters Ideal Filter Functions Ideal vs Practical… Parameters to Watch for… Passive RC Filters Active RC Filters

Why use Analogue Filters? The basic concepts of the electric amplifier were developed in 1915 independantly by Wagner in Germany and Campbell in the United States. In the years since that invention, filter theory and implementation techniques have been developed to a high degree if perfection. Implementing economically an active filter, a filter that uses gain, became possible with the invention of the vacuum tube, and the development of feedback theory by Black, Bode, and others in the early 1930 s.

Why use Analogue Filters? The present era if wide use of high-quality lowcost discrete analogue active filters is due to the development of the inexpensive monolithic operational amplifier by Widlar in 1967. Analogue active filters always use gain and capacitors. In practical discrete active filters, resistors are also used and gain is obtained from the op-amp.

Why use Analogue Filters? To be able to decide which components to use, and whether to use an active filter in preference to a filter assembled entirely out of passive components, we must consider factors such as the following: i. The technology desired for the system implementation ii. Availability of dc supplies for the active devices, and power consumption iii. Cost iv. The range of frequency of operation v. The sensitivity to parameter changes and stability vi. Weight and size of implemented circuit

Types of Filters are classified according to the functions they are to perform. Over the frequency range of interest we define passbands and stopbands. Lowpass filter characteristic: The passband extends from ω = 0 to ω = ωc, where ωc is known as the cutoff frequency. Highpass filter characteristic: The complement of lowpass filter in that the frequency range from 0 to ωc is the stopband from ωc to infinity is the passband.

Types of Filters Bandpass filter characteristics: The frequencies extending from ω1 to ω2 are passed, while signals at all other frequencies are stopped. Bandstop filter characteristic: The complement of the bandpass filter where signal components at the frequencies from ω1 to ω2 are stopped and all others are passed. These filters are also sometimes referred to as notch filters because of the “notch” in their transmission characteristic.

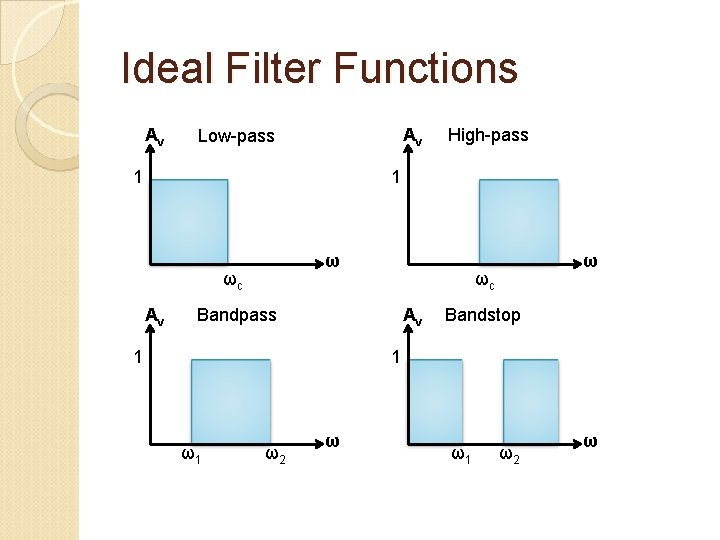
Ideal Filter Functions Av Av Low-pass 1 High-pass 1 ω ωc Av ωc Bandpass Av 1 ω Bandstop 1 ω1 ω2 ω

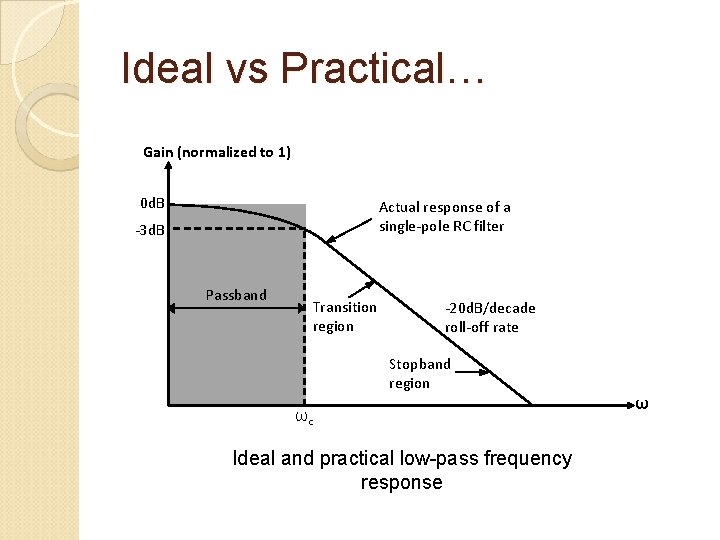
Ideal vs Practical… Gain (normalized to 1) 0 d. B Actual response of a single-pole RC filter -3 d. B Passband Transition region -20 d. B/decade roll-off rate Stopband region ωc Ideal and practical low-pass frequency response ω

Parameters to Watch for… Critical (cutoff) frequency, ωc Defines the end of the passband is normally specified at the point where the response drops – 3 d. B (70. 7%) from the passband response. Quality factor, Q For low-pass and high-pass filters, Q represents the pole quality. For bandpass and bandstop filters, Q is defined as the ratio of the mid frequency to the bandwidth between the two -3 d. B points.

Passive RC Filters VIn R VOut C Sketch the graphs for frequency response and phase response of the RC low-pass filter.

Passive RC Filters VIn R VOut C Also, prove that the transfer function T(s) for the circuit above is given by the following:

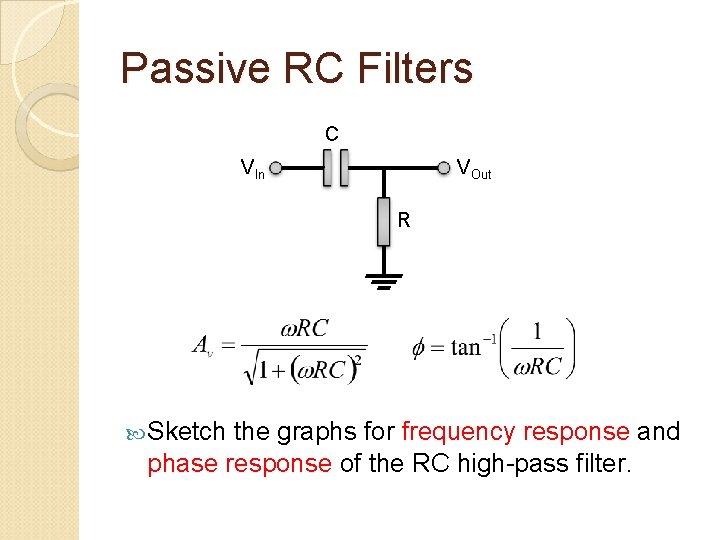
Passive RC Filters C VIn VOut R Sketch the graphs for frequency response and phase response of the RC high-pass filter.

Passive RC Filters C VIn VOut R Also, prove that the transfer function T(s) for the circuit above is given by the following:

Passive RC Filters Prove that at critical frequency, ωc, the output from both circuits are attenuated by -3 d. B. VIn R VOut C C VIn (a) Low-pass VOut R (b) High-pass

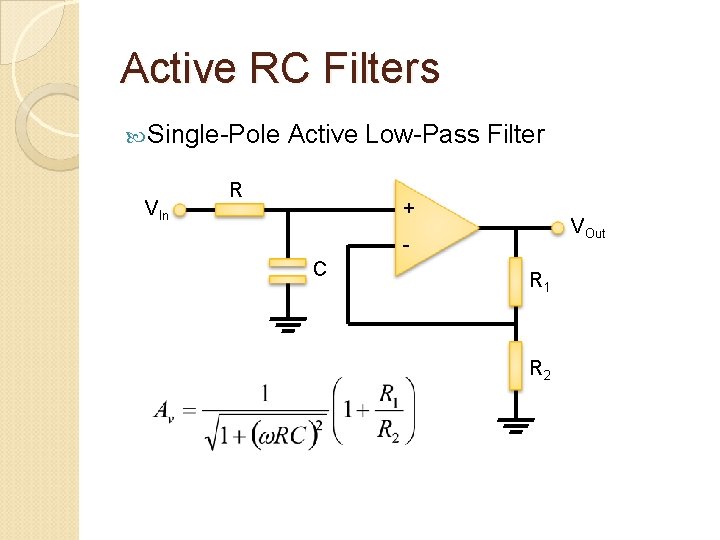
Active RC Filters Single-Pole VIn Active Low-Pass Filter R + VOut C R 1 R 2

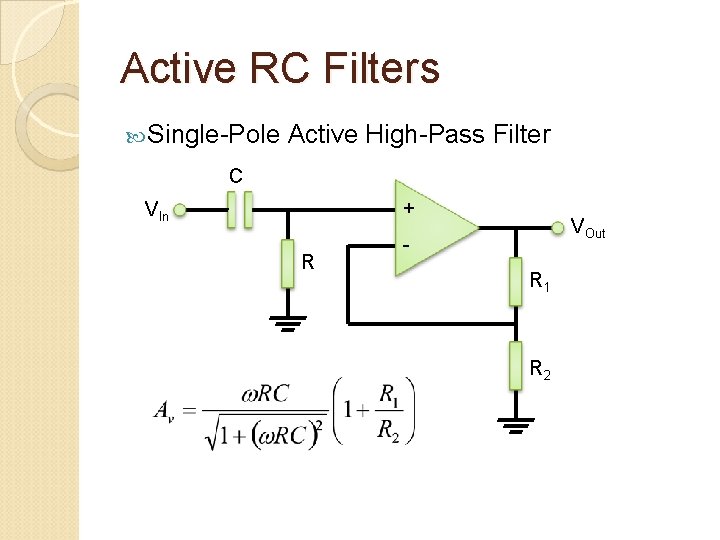
Active RC Filters Single-Pole Active High-Pass Filter C + VIn R VOut R 1 R 2

Further Reading… Schaumann, R. , Van Valkenburg, M. E. (2001). Design of Analog Filters. Oxford University Press. ü Chapter 1 & 3 2. Floyd, T. L. , (2008). Electronic Devices: Conventional Current Version. 8 th Ed. Prentice Hall. ü Chapter 15 3. Karki, J. (1999). Analysis of the Sallen-Key Architecture: Application Report. Texas Instruments. 1.