Bioinformatics Sequence classification profiles patterns and motifs Multiple

Bioinformatics Sequence classification - profiles, patterns and motifs Multiple alignments UL, 2019, Juris Viksna

Topics ü Profiles, patterns and motifs: the sequence classification problem ü profiles and their use ü patterns/motifs ü HMMs ü ü Multiple sequence alignment the problem description ü scoring funktions ü DP algorithm ü heuristic methods (star alignment, progressive alignment, tree alignment) ü improvement of alignments ü

MSA - Piemērs [Adapted from R. Shamir]

Sequence classification Given a set of homologous sequences together with alignment (later about how to find it : ) We want to find a “characterisation” of this group of sequences, which we then could compare with other sequences

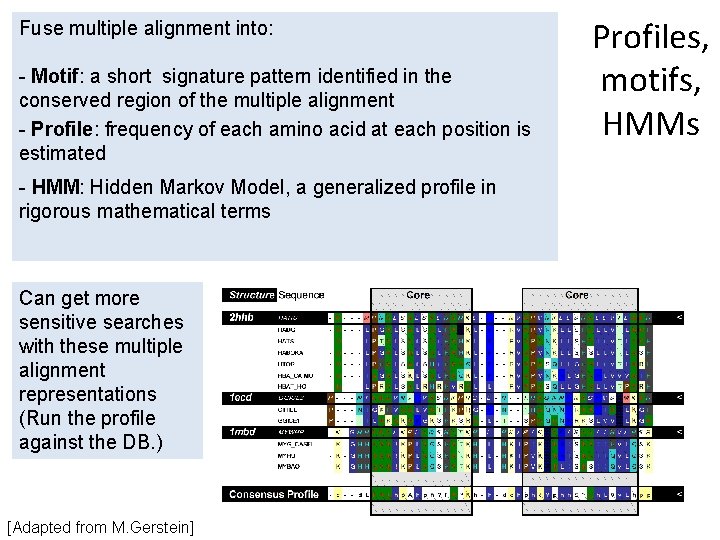
Fuse multiple alignment into: - Motif: a short signature pattern identified in the conserved region of the multiple alignment - Profile: frequency of each amino acid at each position is estimated - HMM: Hidden Markov Model, a generalized profile in rigorous mathematical terms Can get more sensitive searches with these multiple alignment representations (Run the profile against the DB. ) [Adapted from M. Gerstein] Profiles, motifs, HMMs

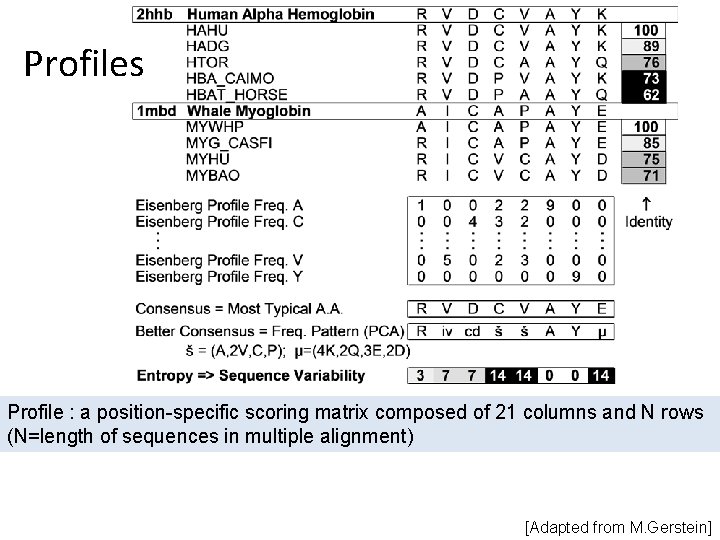
Profiles Profile : a position-specific scoring matrix composed of 21 columns and N rows (N=length of sequences in multiple alignment) [Adapted from M. Gerstein]

PFSearch- Initial alignment and profile >sw: DSBA_PSESM/1 -209 MR---NLIISAALVAASLFGMSAQAAEPIESGKQYVELTSAVPVAVPGKI EVI-ELFWYGCPHCYAFEPTI--N-PWVEKLPSDVNFVRIPAMFGGPWDA -HGQLFITLDTM----GVE---- HKVHAAVFEAIQKGGKRLTDKND MADFVAT----QGVNKDDFLKTF-DSFAVKGKIAQYKELAKKYEVTGVPT MIVNGKYRFDLGSAGGPEKTLQ------VADQLIDKERAA >sw: DSBA_SALTY/1 -206 MK---KIWL---ALAGMVLAFSASAAQ-ISDGKQYITLDKP-- V—AGEP QVL-EFFSFYCPHCYQFEEVLHVSDNVKKKLPEGTKMTKYHVEFLGPLGK ELTQAWAVAMAL----GVE----DKVTVPLFEAVQKTQT-VQSAAD IRKVFVD----AGVKGEDYDAAW-NSFVVKSLVAQQEKAAADLQLQGVPA MFVNGKYQINPQGMDTSSMDVFVQQYADTVKYLVD- ---K >sw: DSBA_ENTAM/3 -202 AKWINSIFKSVVLTAALALPFTAS- -A-FTEGTDYMVLEKPIP--DAD-K TLI-KVFSYACPFCYKYDKAV—TGPVADKVADLVTFVPFHLETKGEYGK QASELFAVTMAKDKAAGVSLFDEKSQFKKAKFAWYAAYHDKKERWSDGKD PAAFLKTGLDAAGMSQAEFEAAL-KEPAVQQTLQKWKAAYEVAKIQGVPA VVNGKYLI---------------Y >sw: DSBA_LEGPN/11 -222 ---------LMPMTALATQ-FIEGKDYQTVASAQLSTNKDKT PLITEFFSYGCPWCYKIDAPL--N-DWATRMGKGAHLERVPVVFKPNWDL -YAKAYYTAKTL----AMS---- DKMNPILFKAIQEDKNPLATKQS MVDFFVA----HGVDREIAKSAFENSPTIDMRVNSGMSLMAHYQINAVPA FVVNNKYKTDLQMAGSEERLFE------ILNYLVRK--SA

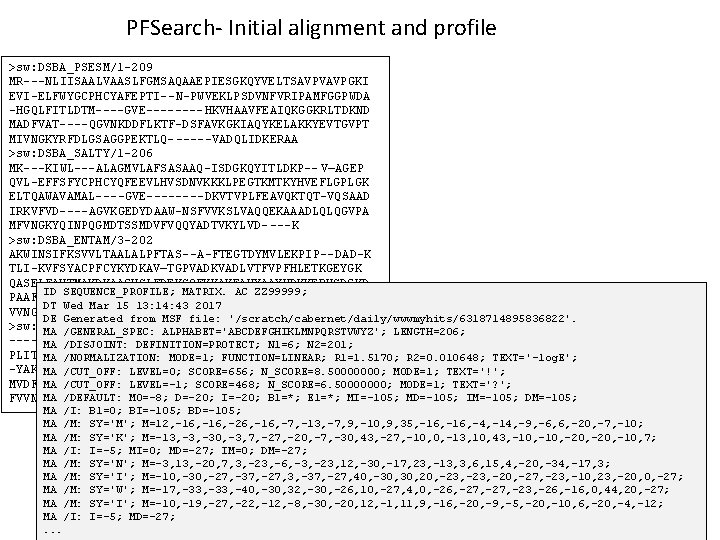
PFSearch- Initial alignment and profile >sw: DSBA_PSESM/1 -209 MR---NLIISAALVAASLFGMSAQAAEPIESGKQYVELTSAVPVAVPGKI EVI-ELFWYGCPHCYAFEPTI--N-PWVEKLPSDVNFVRIPAMFGGPWDA -HGQLFITLDTM----GVE---- HKVHAAVFEAIQKGGKRLTDKND MADFVAT----QGVNKDDFLKTF-DSFAVKGKIAQYKELAKKYEVTGVPT MIVNGKYRFDLGSAGGPEKTLQ------VADQLIDKERAA >sw: DSBA_SALTY/1 -206 MK---KIWL---ALAGMVLAFSASAAQ-ISDGKQYITLDKP-- V—AGEP QVL-EFFSFYCPHCYQFEEVLHVSDNVKKKLPEGTKMTKYHVEFLGPLGK ELTQAWAVAMAL----GVE----DKVTVPLFEAVQKTQT-VQSAAD IRKVFVD----AGVKGEDYDAAW-NSFVVKSLVAQQEKAAADLQLQGVPA MFVNGKYQINPQGMDTSSMDVFVQQYADTVKYLVD- ---K >sw: DSBA_ENTAM/3 -202 AKWINSIFKSVVLTAALALPFTAS- -A-FTEGTDYMVLEKPIP--DAD-K TLI-KVFSYACPFCYKYDKAV—TGPVADKVADLVTFVPFHLETKGEYGK QASELFAVTMAKDKAAGVSLFDEKSQFKKAKFAWYAAYHDKKERWSDGKD ID SEQUENCE_PROFILE; MATRIX. AC ZZ 99999; PAAFLKTGLDAAGMSQAEFEAAL-KEPAVQQTLQKWKAAYEVAKIQGVPA DT Wed Mar 15 13: 14: 43 2017 VVNGKYLI---------------Y DE Generated from MSF file: '/scratch/cabernet/daily/wwwmyhits/6318714895836822'. >sw: DSBA_LEGPN/11 -222 MA /GENERAL_SPEC: ALPHABET='ABCDEFGHIKLMNPQRSTVWYZ'; LENGTH=206; ---------LMPMTALATQ-FIEGKDYQTVASAQLSTNKDKT MA /DISJOINT: DEFINITION=PROTECT; N 1=6; N 2=201; PLITEFFSYGCPWCYKIDAPL--N-DWATRMGKGAHLERVPVVFKPNWDL MA /NORMALIZATION: MODE=1; FUNCTION=LINEAR; R 1=1. 5170; R 2=0. 010648; TEXT='-log. E'; -YAKAYYTAKTL----AMS-------DKMNPILFKAIQEDKNPLATKQS MA /CUT_OFF: LEVEL=0; SCORE=656; N_SCORE=8. 50000000; MODE=1; TEXT='!'; MVDFFVA----HGVDREIAKSAFENSPTIDMRVNSGMSLMAHYQINAVPA MA /CUT_OFF: LEVEL=-1; SCORE=468; N_SCORE=6. 50000000; MODE=1; TEXT='? '; MA /DEFAULT: M 0=-8; D=-20; I=-20; B 1=*; E 1=*; MI=-105; MD=-105; IM=-105; DM=-105; FVVNNKYKTDLQMAGSEERLFE------ILNYLVRK--SA MA /I: MA /M: MA /M: MA /I: . . . B 1=0; BI=-105; BD=-105; SY='M'; M=12, -16, -26, -16, -7, -13, -7, 9, -10, 9, 35, -16, -4, -14, -9, -6, 6, -20, -7, -10; SY='K'; M=-13, -30, -3, 7, -20, -7, -30, 43, -27, -10, 0, -13, 10, 43, -10, -20, -10, 7; I=-5; MI=0; MD=-27; IM=0; DM=-27; SY='N'; M=-3, 13, -20, 7, 3, -23, -6, -3, -23, 12, -30, -17, 23, -13, 3, 6, 15, 4, -20, -34, -17, 3; SY='I'; M=-10, -30, -27, -37, -27, 3, -37, -27, 40, -30, 20, -23, -20, -27, -23, -10, 23, -20, 0, -27; SY='W'; M=-17, -33, -40, -30, 32, -30, -26, 10, -27, 4, 0, -26, -27, -23, -26, -16, 0, 44, 20, -27; SY='I'; M=-10, -19, -27, -22, -12, -8, -30, -20, 12, -1, 11, 9, -16, -20, -9, -5, -20, -10, 6, -20, -4, -12; I=-5; MD=-27;

Profiles Matrix M of size 20 n (or 21 n), where m(i, j) is probability that the j-th aa could be found in the i-th position (and 21 st “aa” could be used for gap : ) For given aa sequence a 1. . . an, the probability that it corresponds to the given profile is p = m(1, a 1)·. . . ·m(n, an). Or, provided that the matrix contains sequence logarithms, the probability is: p = exp(m(1, a 1)+. . . +m(n, an)).

Computing of profiles [Adapted from M. Singh

Computing of profiles [Adapted from M. Singh]

Search using profiles [Adapted from M. Singh]

Extensions of profiles Other modifications are also possible [Adapted from M. Singh]

Links to databases and search tools Currently functional profile (and similar) searches: http: //myhits. isb-sib. ch/cgi-bin/profile_search Pfam: protein family (actually MA and HMM) database: http: //pfam. xfam. org/

Motifs/patterns - PROSITE Database of protein families and domains http: //www. expasy. org/prosite/ 29. 06. 2016 - 1309 patterns, 1161 profiles, 1175 Pro. Rules +----------+ +-------------+ | | x(4)-C-x(0, 48)-C-x(3, 12)-C-x(1, 70)-C-x(1, 6)-C-x(2)-G-a-x(0, 21)-G-x(2)-C-x | | ****************** +----------+ 'C': 'G': 'a': '*': 'x': conserved cysteine involved in a disulfide bond. often conserved glycine often conserved aromatic amino acid position of both patterns. any residue -Consensus pattern: C-x-C-x(5)-G-x(2)-C [Adapted from M. Gerstein]

Motifs/patterns - PROSITE How to find PROSITE pattern for sequence alignment: GRABCDA-B GRADC-A-B GAABCDA-B GRABCDA-C GAABCCA-B GRA-CDA-C GRABBDA-B G_ABCDA-B GRABBDA-C GRABCCA-B Sample pattern: [LIY]-x-A-C-V-[DNQ]-x(3)-[RS]-x(2, 4)-[PS]

“Generalized” profiles

“Fair Casino” Problem : ) [Adapted from P. Pevzner]

HMM - definition HMM for “Casino Problem”: [Adapted from P. Pevzner]

HMM for protein sequences

HMM for protein sequences [Adapted from R. Shamir]

Alignment of HMMs [Adapted from J. Söding]

HMM – algorithmic problem Easy (DP) Hard : (

Sequence alignment with HMM [Adapted from P. Pevzner]

HMM – Forward Algorithm [Adapted from M. Craven]

HMM – Viterbi Algorithm [Adapted from M. Craven]

HMM – Baum-Welch Algorithm We omit here a more detailed discussion on this one [Adapted from A. Mc. Callum]

Multiple sequence alignment (MSA) Identification of homologs with pairwise comparisons: similarity score > 30% similarity score 15 -30% OK ? ? ? • Weak similarity becomes statistically significant, if the same alignment is conserved for many pairs of sequences • Well characterises protein domains • Well characterises gene regulatory regions

MSA – short history • Practical and usable methods only since 1987 • Before 1987 computed manually • The main problem: DP methods require complexity exponential with the number of sequences • The first practical method: D. Sankoff (1987) was based on phylogenetics

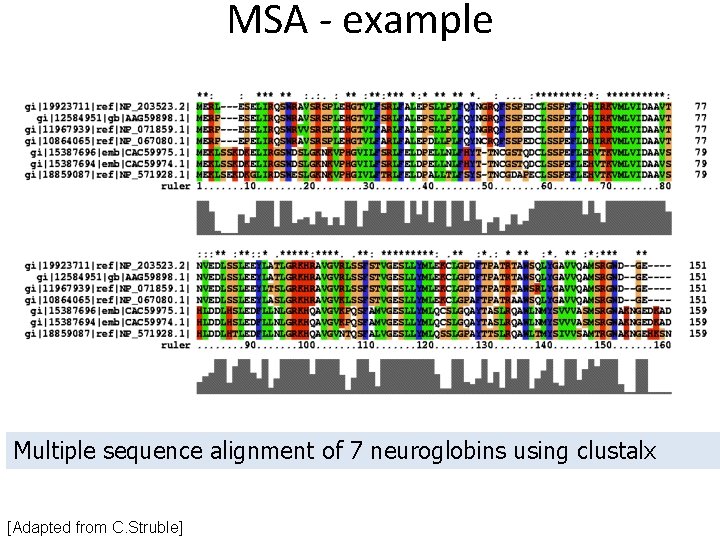
MSA - example Multiple sequence alignment of 7 neuroglobins using clustalx [Adapted from C. Struble]

MSA - Piemērs [Adapted from R. Shamir]

MSA – the exact formulation of the problem? • There is no generally accepted definition • Approximately - “align” sequences in such a way that the aligned part is the longest possible • If we try to formulate it more precisely, several alternative variants are possible • From the practical perspective it seems it is not too important which variant is chosen. And most algorithms are just heuristic. . . • Related question – how to score MSA?

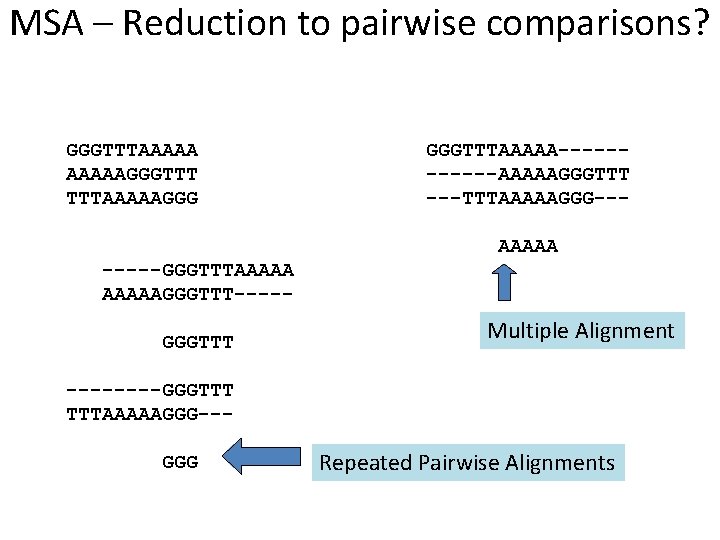
MSA – Reduction to pairwise comparisons? GGGTTTAAAAAGGGTTT TTTAAAAAGGG GGGTTTAAAAA------AAAAAGGGTTT ---TTTAAAAAGGG--AAAAA -----GGGTTTAAAAAGGGTTT----GGGTTT Multiple Alignment ----GGGTTT TTTAAAAAGGG--GGG Repeated Pairwise Alignments

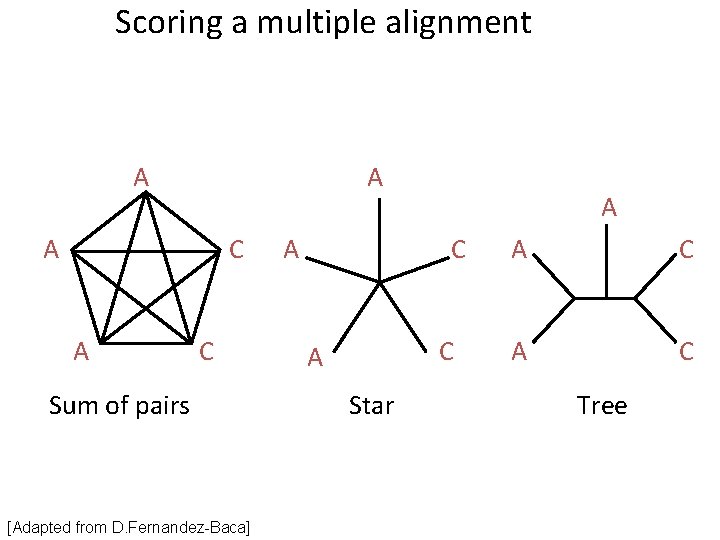
Scoring a multiple alignment A A A C Sum of pairs [Adapted from D. Fernandez-Baca] A A C C A Star A C Tree

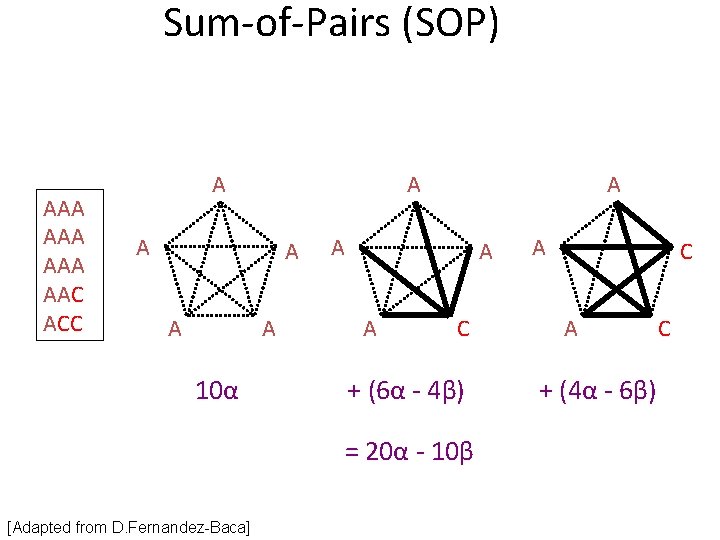
Sum-of-Pairs (SOP) AAA AAA AAC ACC A A A 10α A A C + (6α - 4β) = 20α - 10β [Adapted from D. Fernandez-Baca] A C A + (4α - 6β) C

Induced pairwise alignments • S 1: • S 2: • S 3: S - T I S C T G - S - N I L - T I – C N G S S - N I L R T I S C S G F S Q N I Induced pairwise alignment of S 1, S 2: S 1 S 2 S T I S C T G - S N I L T I – C N G S S N I [Adapted from D. Fernandez-Baca]

Sum-of-Pairs alignment score Score of multiple alignment S = ∑i <j score(Si, Sj), where score(Si, Sj) = score of induced pairwise alignment Instead of sum of scores, we could optimise e. g. minimal value. This could further be made more complicated, by adding more complex scoring for gap penalties etc. [Adapted from D. Fernandez-Baca]

MSA and DP algorithm for two sequences can be easily generalized to arbitrary number of sequences For example, for three sequences X, Y, W define: C[i, j, k] = optimal alignment score for sequences X[1. . i], Y[1. . j], W[1. . k] In the same way as for 2 sequences, we can separate alignments in classes according to the last matched symbols [Adapted from D. Fernandez-Baca]

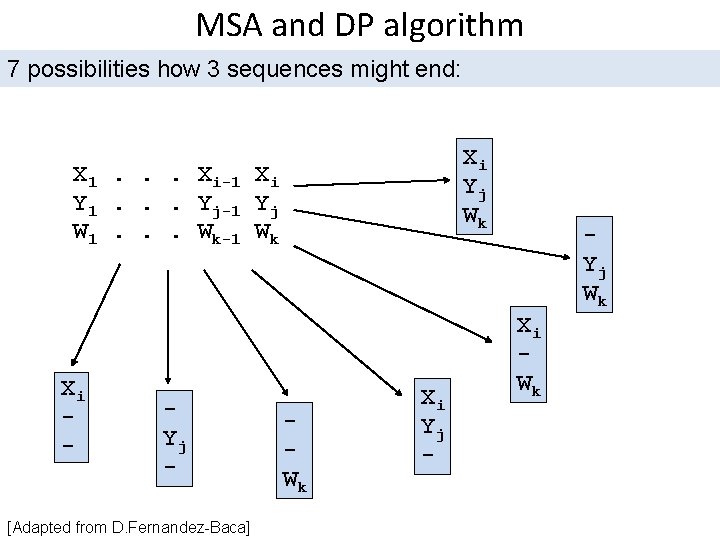
MSA and DP algorithm 7 possibilities how 3 sequences might end: Xi Yj Wk X 1. . . Xi-1 Xi Y 1. . . Yj-1 Yj W 1. . . Wk-1 Wk Xi - Yj - [Adapted from D. Fernandez-Baca] Wk Xi Yj - Yj Wk Xi Wk

MSA and DP algorithm 7 possibilities to obtain C[i, j, k]: C[i, j, k] C[i-1, j, k-1] C[i-1, j-1, k-1] C[i-1, j, k-1] For 3 sequences of length n, time is proportional to n 3 Enumerate all possibilities and choose the best one [Adapted from D. Fernandez-Baca]

MSA and DP algorithm A S V [Adapted from G. Church]

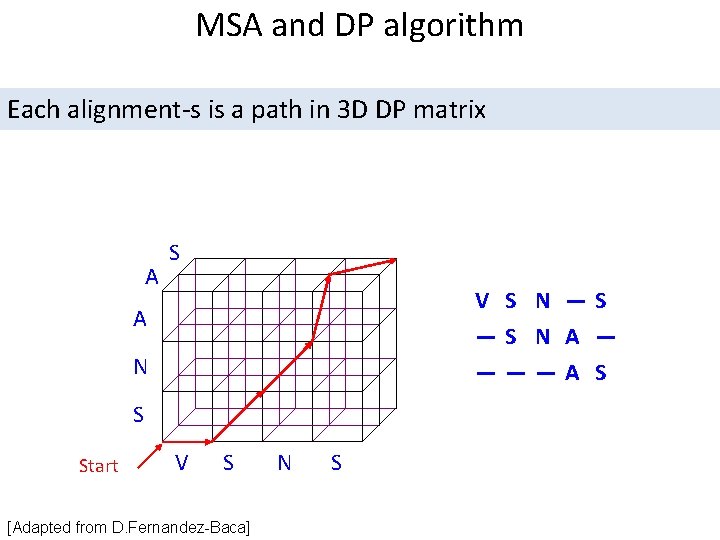
MSA and DP algorithm Each alignment-s is a path in 3 D DP matrix A S V S N —S —S N A — ———A S A N S Start V S [Adapted from D. Fernandez-Baca] N S

MSA and DP - Complexity O(nk) “cells” to be filled Each cell depends from O(2 k) other Each “SOP-score” computation requires O(k 2) time Total complexity: O(k 2 2 k nk) – exponential from the number of sequences : ( • MSA with “SOP-score” (or with any other “interesting score”) is NP-complete problem • • [Adapted from C. Struble]

MSA and DP - Complexity • For k sequences of length n, dynamic programming algorithm does (2 k-1) nk operations – Example: 6 sequences of length 100 require 600 63 calculations • Space for table is nk • Implementations (e. g. , Wash. U MSA 2. 1) use tricks and only search subset of dynamic programming table – Even this is expensive. E. g. , Baylor CM Search launcher limits MSA to 8 sequences of 800 characters and 10 minutes processing time [Adapted from D. Fernandez-Baca]

Restricted MA DP • A possible way to increase efficiency of MA: • Construct “Progressive MA” m • Use restricted MA DP, restricted to radius R from m Time complexity: O(2 N RN-1 L) [Adapted from S. Batzoglou]

Forward dynamic programming [Adapted from R. Shamir]

Problems with SOP scoring • Pair-wise comparisons can over-score evolutionarily distant pairs. • Reason: For 3 or more sequences, SP scoring does not correspond to any evolutionary tree. But not: [Adapted from D. Fernandez-Baca]

Problems with SOP scoring Solutions: • Use weights to incorporate evolution in sum of pairs scoring: – Some pairwise alignments are more important than others • E. g. , more important to have a good alignment between mouse and human sequences than mouse and bird – Assign different weights to different pair-wise alignments. • Weight decreases with evolutionary distance. • Use star tree approach – one sequence is assigned as the ancestor and all others are contrasted it.

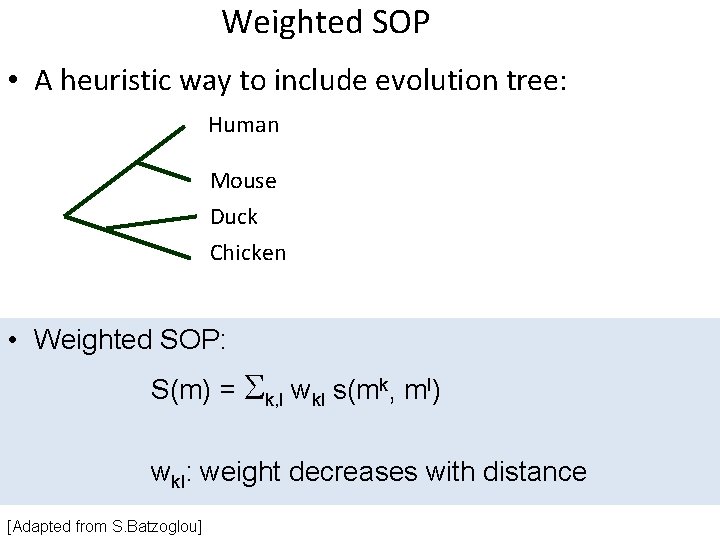
Weighted SOP • A heuristic way to include evolution tree: Human Mouse Duck Chicken • Weighted SOP: S(m) = k, l wkl s(mk, ml) wkl: weight decreases with distance [Adapted from S. Batzoglou]

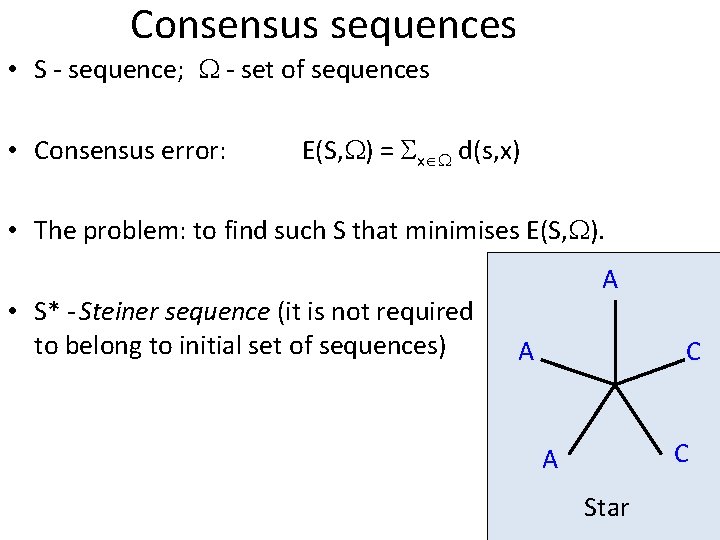
Consensus sequences • S - sequence; - set of sequences • Consensus error: E(S, ) = x d(s, x) • The problem: to find such S that minimises E(S, ). • S* - Steiner sequence (it is not required to belong to initial set of sequences) A A C C A Star

Consensus vs Steiner sequences [Adapted from R. Shamir]

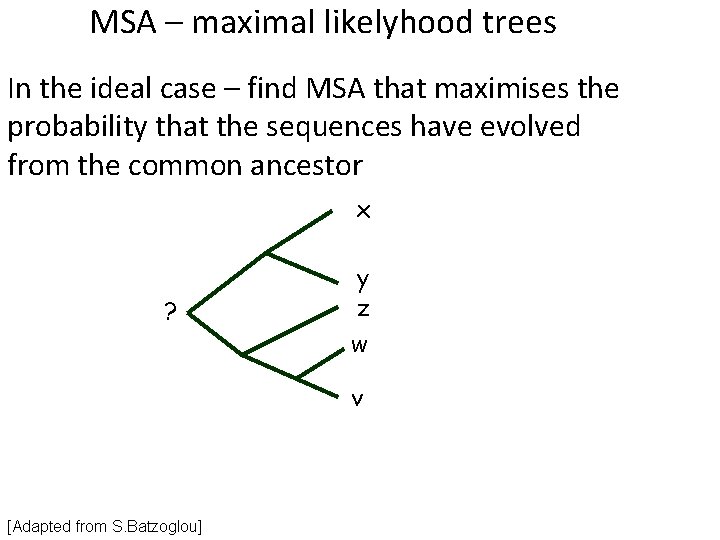
MSA – maximal likelyhood trees In the ideal case – find MSA that maximises the probability that the sequences have evolved from the common ancestor x ? y z w v [Adapted from S. Batzoglou]

Approximation algorithms – for given optimisation problem find not the best possible solution, but the one that is no more than x times worse than the best G – set of k “stars” G is balanced, if it contains each pair of sequences p times for some p 1 Theorem (Gusfield, 1993) At least one of the stairs in the given balanced set will give a 2 – 2/n approximation of MSA. Such 2 -approximation is not good enough for biologists though

Heuristic methods Heuristic algorithms – in principle do not guarantee any “good” result, but are based on “intelligent considerations” and sometimes could produce “useful” results Some heuristic methods: • Star Alignment • Progressive MSA • Tree Alignment • The programs used in practice tend to be very “heuristic” and do not correspond to strict “textbook versions”

Star Alignment [Adapted from R. Shamir]

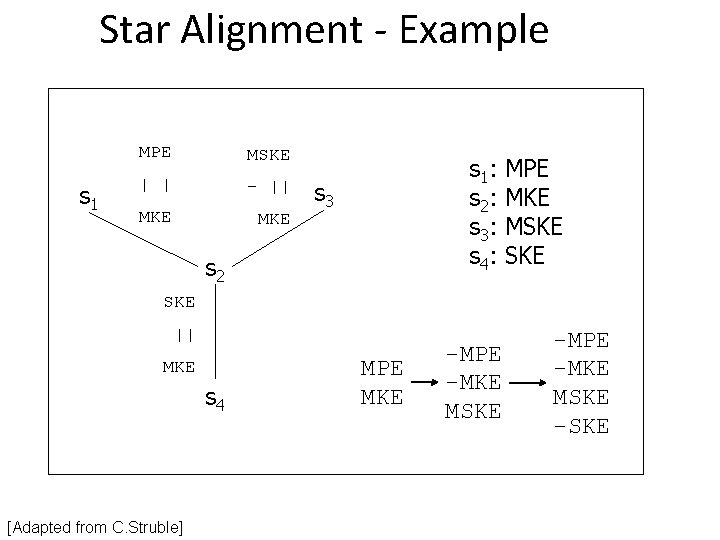
Star Alignment - Example s 1 MPE MSKE | | - || MKE s 1 : s 2 : s 3 : s 4 : s 3 s 2 MPE MKE MSKE SKE || MKE s 4 [Adapted from C. Struble] MPE MKE -MPE -MKE MSKE -SKE

Star Alignment - Complexity • Assume all sequences have length n • O(n 2) time to find global alignment • O(k) global alignments • Using “good” data structure to join alignments, such joins require O(kl) time, where l is maximal length of alignments, this gives total time O(kn 2+k 2 l) [Adapted from C. Struble]

Progressive Alignment • General idea: – – Align two of the sequences xi, xj Fix that alignment Align a third sequence xk to the alignment xi, xj Repeat until all sequences are aligned • Running Time: O( N L 2 ) Not the same as star alignment we try to find the best match with an alignment, not a particular sequence [Adapted from S. Batzoglou]

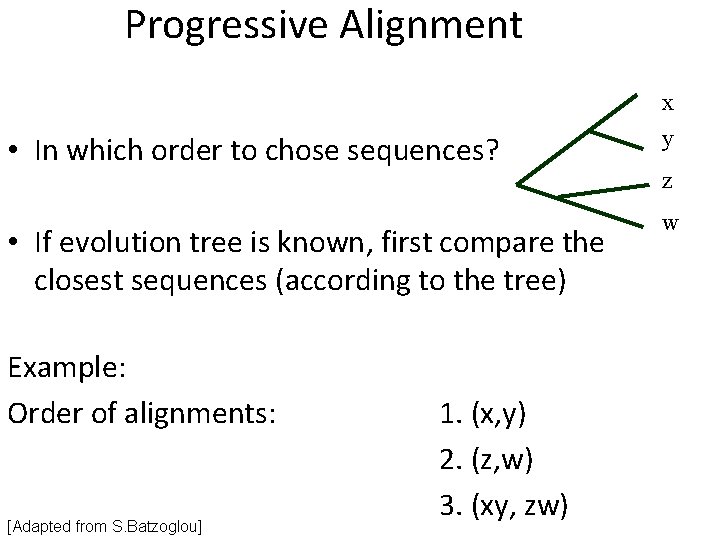
Progressive Alignment • In which order to chose sequences? • If evolution tree is known, first compare the closest sequences (according to the tree) Example: Order of alignments: [Adapted from S. Batzoglou] 1. (x, y) 2. (z, w) 3. (xy, zw) x y z w

Progressive Alignment - Most MA programs are based on this principle - Initial hypothesis about the phylogenetic tree is obtained on the basis of sequence pair comparisons - Build the tree incrementally, starting with the closest sequence pairs - Follow the tree starting from the leaves to construct MA - Sufficiently fast - “Sensitive” - Heuristic, there is no “exact” mathematical description of the approach - “Reasonably good” for biologists – often produces MA that is difficult to improve manually

Tree Alignments • Represent k sequences with a tree with k leaves • Compute the weight of each edge (distance between the sequences) • The weight of tree is the sum of weights of all the edges • Find the tree with minimal weight I. e. something very similar to finding phylogenetic tree NP-complete problem [Adapted from C. Struble]

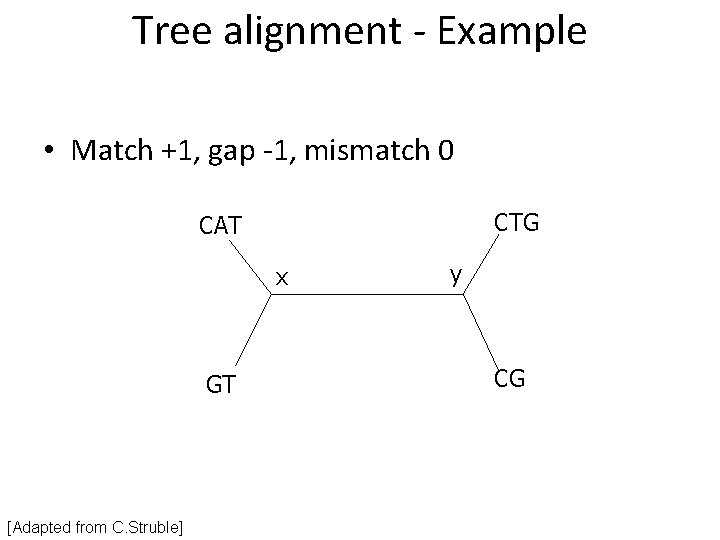
Tree alignment - Example • Match +1, gap -1, mismatch 0 CTG CAT x GT [Adapted from C. Struble] y CG

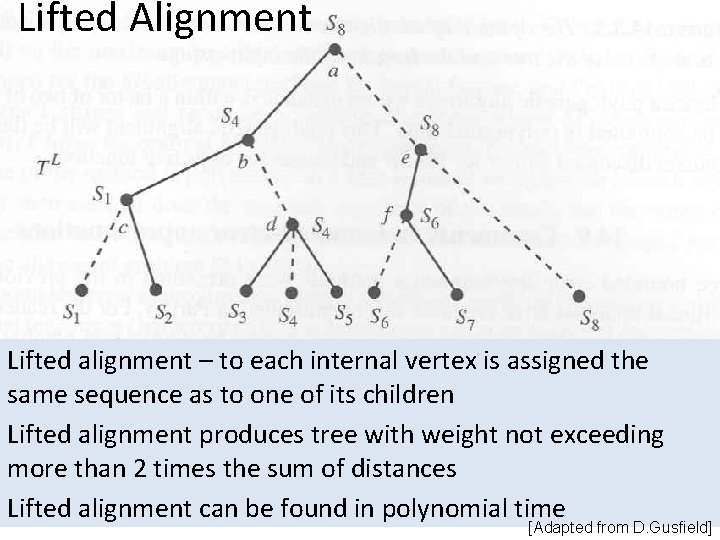
Lifted Alignment Lifted alignment – to each internal vertex is assigned the same sequence as to one of its children Lifted alignment produces tree with weight not exceeding more than 2 times the sum of distances Lifted alignment can be found in polynomial time [Adapted from D. Gusfield]

Progressive MA - Problems Local minimum problem • This is due to “greedy nature of alignment” – aligned sequences are never changed • Better initial tree produces better alignments (UPGMA neighbour-joining tree method often used) The problem of parameter choice • Due to the same set of parameters used in different situations

Progressive MSA - Problems One of the problems with progressive alignments – initial alignments are not changed, even if there is a need to do it. Example: • • x: y: GAAGTT GAC-TT Frozen! • • z: w: GAACTG GTACTG Now clear that [Adapted from S. Batzoglou] y = GA-CTT

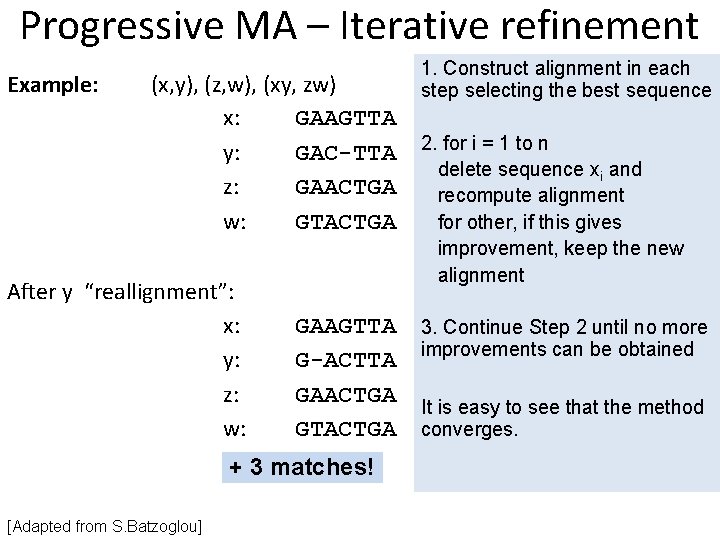
Progressive MA – Iterative refinement Example: (x, y), (z, w), (xy, zw) x: GAAGTTA y: GAC-TTA z: GAACTGA w: GTACTGA After y “reallignment”: x: y: z: w: GAAGTTA G-ACTTA GAACTGA GTACTGA + 3 matches! [Adapted from S. Batzoglou] 1. Construct alignment in each step selecting the best sequence 2. for i = 1 to n delete sequence xi and recompute alignment for other, if this gives improvement, keep the new alignment 3. Continue Step 2 until no more improvements can be obtained It is easy to see that the method converges.

Progressive MA – Iterative refinement No so good example. . . x: y 1: y 2: y 3: z: w: [Adapted from S. Batzoglou] GAAGTTA GAC-TTA GAACTGA GTACTGA Realigment of any single yi does not change anything…

Restricted MA DP • A possible way to increase efficiency of MA: • Construct “Progressive MA” m • Use restricted MA DP, restricted to radius R from m Time complexity: O(2 N RN-1 L) [Adapted from S. Batzoglou]

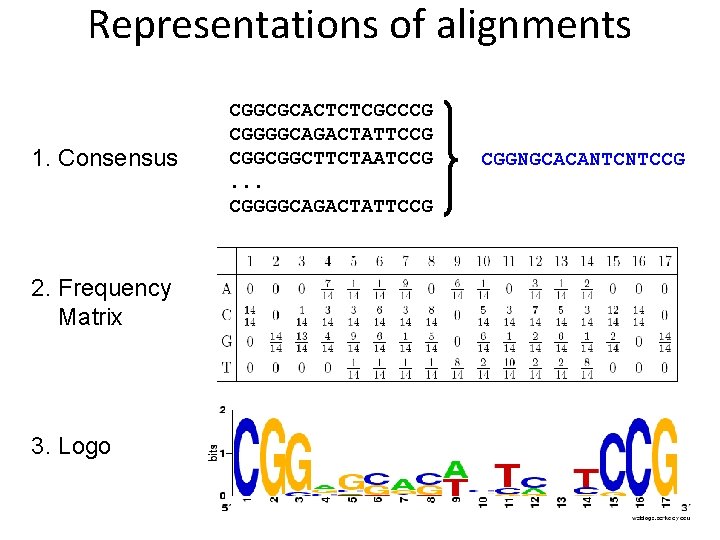
Representations of alignments 1. Consensus 2. Frequency Matrix 3. Logo CGGCGCACTCTCGCCCG CGGGGCAGACTATTCCG CGGCGGCTTCTAATCCG. . . CGGGGCAGACTATTCCG CGGNGCACANTCNTCCG

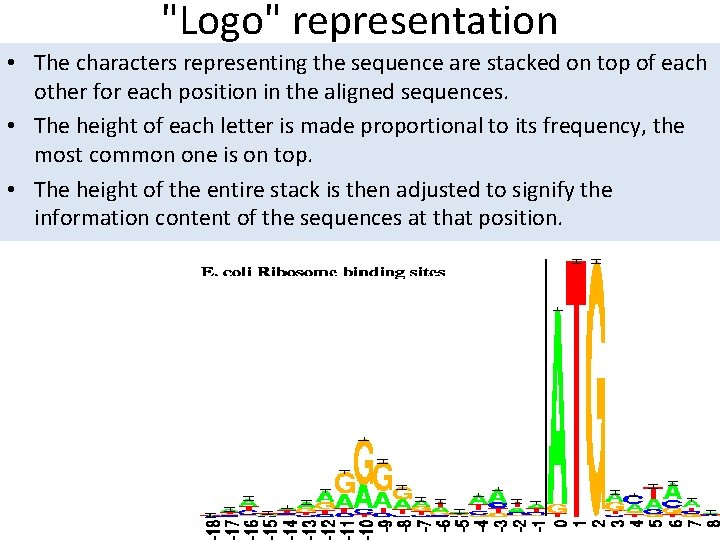
"Logo" representation • The characters representing the sequence are stacked on top of each other for each position in the aligned sequences. • The height of each letter is made proportional to its frequency, the most common one is on top. • The height of the entire stack is then adjusted to signify the information content of the sequences at that position.

Clustal(W) – one of the first widely used MA programs

Clustal. W - the most popular MA program (until recently…) Algorithm: – Find all dij: alignment dist (xi, xj) – Construct a tree (Neighbor-joining hierarchical clustering) – Align nodes in order of decreasing similarity + a large number of heuristics [Adapted from S. Batzoglou] http: //www. ebi. ac. uk/clustalw/

T-coffee

HHalign Not directly MA tool (aligns two HMMs instead), but the approach later adapted of Clustal Omega.

HMAFFT

AMAP – simulated annealing based approach. Not a mainstream MA technique, but a couple of new MA methods are still being published each year. Software is still available online.

Clustal Omega

Some test sequences for MA >sp|P 69905|HBA_HUMAN Hemoglobin subunit alpha (Hemoglobin alpha chain) (Alpha-globin) - Homo sapiens (Human). VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHFDLSHGSAQVKGHGK KVADALTNAVAHVDDMPNALSALSDLHAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPA VHASLDKFLASVSTVLTSKYR >tr|Q 61287_MOUSE Alpha-globin - Mus musculus (Mouse). MVLSGEDKSNIKAAWGKIGGHGAEYVAEALERMFASFPTTKTYFPHFDVSHGSAQVKGHG KKVADALASAAGHLDDLPGALSALSDLHAHKLRVDPVNFKLLSHCLLVTLASHHPADFTP AVHASLDKFLASVSTVLTSKYR >tr|Q 28383_HORSE Horse BII alpha-2 globin - Equus caballus (Horse). MVLSAADKTNVKAAWSKVGGHAGEFGAEALERMFLGFPTTKTYFPHFDLSHGSAQVKAHG QKVGDALTLAVGHLDDLPGALSNLSDLHAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTP AVHASLDKFLSSVSTVLTSKYR >sp|P 01966|HBA_BOVIN Hemoglobin subunit alpha (Hemoglobin alpha chain) (Alpha-globin) - Bos taurus (Bovine). VLSAADKGNVKAAWGKVGGHAAEYGAEALERMFLSFPTTKTYFPHFDLSHGSAQVKGHGA KVAAALTKAVEHLDDLPGALSELSDLHAHKLRVDPVNFKLLSHSLLVTLASHLPSDFTPA VHASLDKFLANVSTVLTSKYR

Links to MA programs and services Clustal. W/X dowloads: http: //www. clustal. org/clustal 2/ Clustal. W at Swiss Institute of Bioinformatics: http: //www. ch. embnet. org/software/Clustal. W. html MA programs at EBI: http: //www. ebi. ac. uk/Tools/msa/ Including Clustal Omega: http: //www. ebi. ac. uk/Tools/msa/clustalo/ MA programs at SIB: https: //www. expasy. org/genomics/sequence_alignment