BIOINFORMATICS Data bases Biosequences Structures Genomes DNA Chips

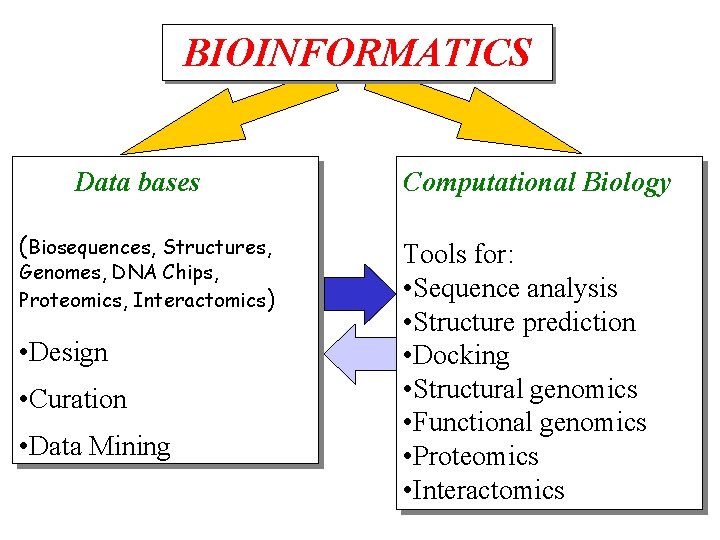
BIOINFORMATICS Data bases (Biosequences, Structures, Genomes, DNA Chips, Proteomics, Interactomics) • Design • Curation • Data Mining Computational Biology Tools for: • Sequence analysis • Structure prediction • Docking • Structural genomics • Functional genomics • Proteomics • Interactomics

The problem: Sequence comparison • How to compare two sequences • How to compare one sequence (target) to many sequences (database search) The solution: Sequence alignment

Why to compare Similarity search is necessary for: • Family assignment • Sequence annotation • Construction of phylogenetic trees • Protein structure prediction

Sequence Alignment Rita Casadio

Types of alignments: • Aligment of Pairs of Sequences • Multiple Sequence Alignment of three or more protein sequences

Pairwise and multiple sequence alignments can be global or local • Globlal: the whole sequence is aligned • Local : only fragments of the sequence are aligned

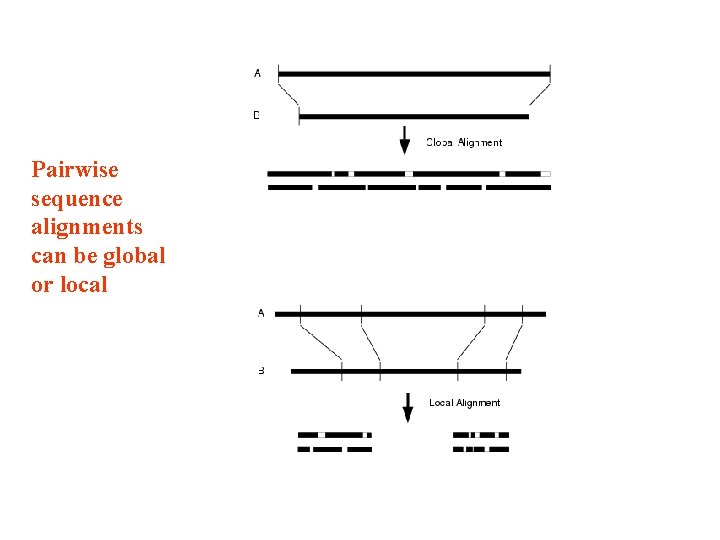
Pairwise sequence alignments can be global or local

A basic concept: Measures of sequence similarity

Given two character strings, two measures of the distance between them are: 1) The Hamming distance defined between two strings of equal length is the number of positions with mismatching characters agtc cgta Hd=2 2) The Levenshtein or edit distance between two strings of not necessarily equal length is the minimal number of edit operations required to change one string into the other, where an edit operation is a deletion, insertion or alteration of a single character in either sequence. A given sequence of edit operations induces an unique alignment, but not viceversa ag-tcc cgctca Ld=3

Scoring schemes A scoring scheme must account for residue substitutions, insertions or deletions (gaps) Scores are measures of sequence similarity (similar sequences have small distances (high scores), dissimilar sequences give large distances (low scores))

Algorithms for optimal aligment can seek either to minimize a dissimilarity measure or maximize a scoring function

For nucleic acid sequences (Genetic Code Scoring) A simple scheme for substitution for nucleic acid sequences: match +1 mismatch -1 More complicated scheme are based on the higher frequency of transition mutations than transverse mutations

Example: a a 20 t 10 g 5 c 5 t g 10 5 20 5 10 c 5 5 10 20 identity=20 high frequency=5 low frequency=10 purine=purine, and pyrimidine=pyrimidine are more common than purine=pyrimidine, or pyrimidine=purine.

For proteins a variety of scoring schemes have been proposed Similarity of physicochemical type (Chemical similarity scoring. Eg. Mc. Lachlan similarity matrix: polar, non polar; size, shape, charge, rare (F)) Substitution matrices

Substitution matrices for proteins • PAM • BLOSUM • Matrices derived from tertiary structure aligment

Derivation of substitution matrices The Dayhoff mutation matrix: As sequence diverge, mutations accumulate. To measure the relative probability of any particular substitution we can count the number of changes in pairs of aligned similar sequences (relative frequency of such changes to form a scoring matrix for substitution) 1 PAM: 1 Percent Accept Mutation two sequences 1 PAM apart have 99% identical residues. One change in any position Collecting statistics from pairs of sequences closely related (1 PAM) and correcting for different aminoacid abundances produces the 1 PAM substitution matrix

For more widely diverged sequences powers of 1 PAM are used PAM 250 (20% overall sequence identity) Different PAMS for different level of sequence identity PAM % Identity 0 30 80 110 200 250 100 75 50 60 25 20 M. Dayhoff (1978) PET 91 (Jones et al. , 1992) is based on 2621 families

Score of mutation i, j log observed i, j mutation rate/ mutation rate expected from aminoacid frequencies log-odds values (x 10) 2 =0. 2 (scaling) log 10= 10^0. 2=1. 6˜ 2 The value is the expectation value of the mutation The probability of two independent mutational events is the product of their probabilities (addition when we consider logs)

PAM 250

The BLOSUM Matrices Henikoff and Henikoff (1991) Best performing in identifying distant relationships, making use of the much larger amount of data that had become available since M. Dayhoff’s work Based on a data base of multiple alignments without gaps for short regions of related sequences. Within each alignment in the data base, the sequences were clustered into groups where the sequences are similar at some threshold value of percentage identity log odds BLOSUM(blocks substitution matrix) BLOSUM 40, 62, 80. .

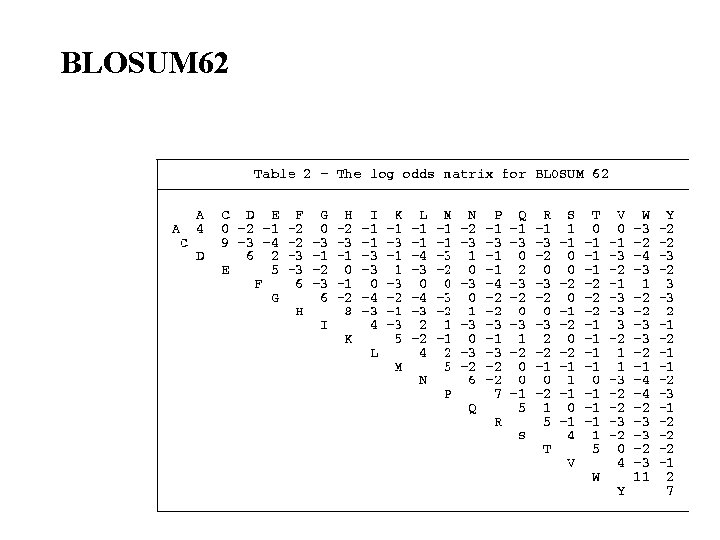
BLOSUM 62

DOTPLOT ANALYSIS a simple picture that gives an overwiev of the similarites between two sequences The doplot is a table or matrix based on scoring schemes

Dotlet - A Java applet for sequence comparisons using the dot matrix method http: //www. isrec. isb-sib. ch/java/dotlet/Dotlet. html

How to search for internal repeats in the sequence

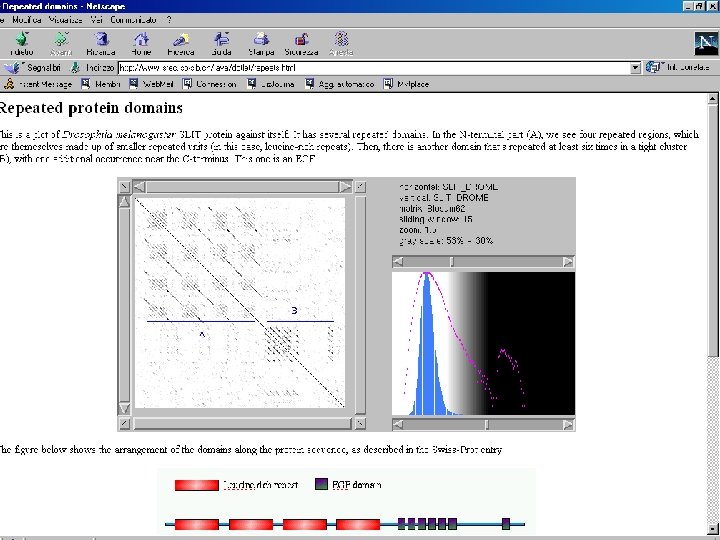
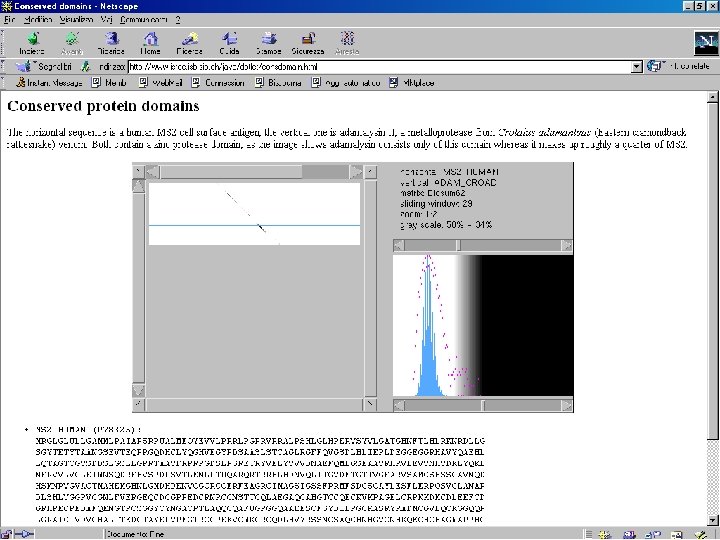
How to search for conserved domains

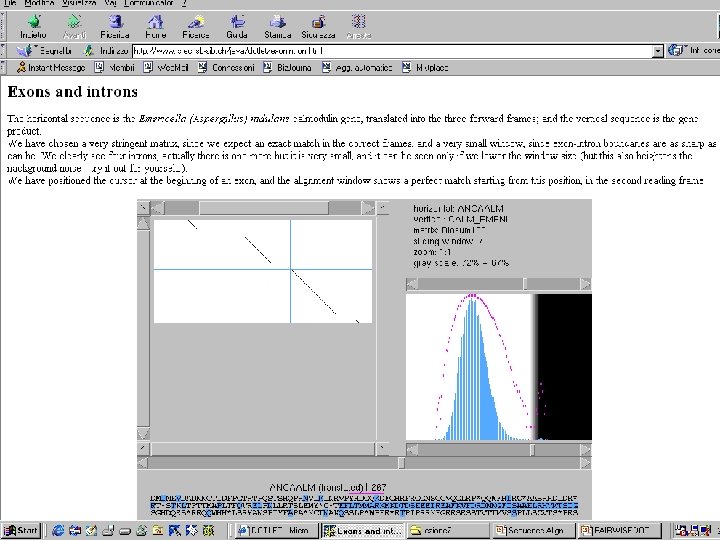
Exons and Introns: How to find them ANCALM (J 05545): TGAATCCCAGTTCAGCTCTTCAGCCTTTCGTGGATAAGAGAAGGCTGAAAGCGGGTCACGTTTTGGACTAAGCGACGCCC TTGCCAGGCATCCAGCTTAGTGGCTGTTGGTTTATTTGTAGAGTCCCCTTAACTCTCCCCCACATCGCCCATCTCC ACCGACGCCTCTCTCGTGTTATTTCTCCCCATTCTCGCTTCATTTCCCATTTTCGAGTTCTGCAATATCCTC ACTAGTATAGCCATGGTACGCCTCACTCGATCATCATCGTTGTTCGTGCGCTCAAACGCATCCGCTGTGCGGGGCA GATCTACTGGTGTCCTCCTGCGTAGATGAGCTGACGACTTCCAGGCCGACTCTCTGACCGAAGAGCAAGTTTCCG AGTACAAGGAGGCCTTCTCCCTATTTGTAAGTGCCATTGGTTACTGTTATATCAAAATCGAATTTGTATTGAGAGTATAC TAATACATTCCGCACTAAACAGGACAAGGATGGCGATGGTTAGTGCATCTGTCCCCCCAGGCTTGATCGCATTCGCCCAG CATGTCTGCTGTAGCTCTATATAACCGTTTCTGACAAACGGCGACAGGCCAGATTACCACTAAGGAGCTTGGCACTGTCA TGCGCTCGGTCAGAATCCTTCAGAGTCTGAGCTTCAGGACATGATCAACGAAGTTGACGCCGACAACAATGGCACC ATTGACTTTCCAGGTACGCGAACTCCCCAATCTACTTCGCACCAGCCTAGAAATGTACTAATGCTAAACAGAGTTCCTTA CCATGATGGCCAGAAAGATGAAGGACACCGATTCCGAGGAGGAAATTCGGGAGGCGTTCAAGGTCTTCGACCGTGACAAC AATGGTTTCATCTCCGCTGCTGAGCTGCGTCATGACCTCGATCGGTGAGAAGCTCACCGATGACGAAGTCGACGA GATGATCCGCGAGGCGGACCAGGATGGCGACGGCCGAATTGACTGTACGTTGGCTCCCCGCTTATCCTTGACCGTAGAAG AGGTATGATACTGATCGGCTGCAGACAACGAATTCGTCCAACTTATGATGCAAAAATAAACGCTCTTACCTTTGATGTTT ATCGTTAGCGAAGAAGGTGTGGACACTTTCCAGCTGTCTCATCTTAGTTGTCATATCATTGAATGTAGCCTATCTGATTG CGGATAAGCAACTGATGGTTGTAACGGCTTCCATTTTGCTCTGACTTCTGAGTACCCTTTTCCTTCATGTTCGTCG ACCATTCTGCTAGTGAGATATGCGTAGAGTTGGGTAGGCTGAATTTACGAGTCTCTGTTGGGGGATATCACATGCTTCAC TACAATCTTTCTCTAC CALM_EMENI (P 19533): ADSLTEEQVSEYKEAFSLFDKDGDGQITTKELGTVMRSLGQNPSESELQDMINEVDADNNGTIDFPEFLTMMARKMKDTD SEEEIREAFKVFDRDNNGFISAAELRHVMTSIGEKLTDDEVDEMIREADQDGDGRIDYNEFVQLMMQK

Sequence Alignment: Methods Rita Casadio

Alignment of pairs of sequences • Dot matrix analysis (dotplot) • The dynamic programming algorithm • Word or K-tuple methods (FASTA, BLAST)

Sequence comparison with gaps Deletions are referred to as ``gaps'', while insertions and deletions are collectively referred to as ``indels''. Insertions and deletions are needed to align accurately even quite closely related sequences such as the and globins The naive approach to finding the best alignment of two sequences including gaps is to generate all possible alignments, add up the scores for equivalencing each amino acid pair in each alignment then select the highest scoring alignment. However, for two sequences of 100 residues there alternative alignments so such an approach would be time consuming and infeasible for longer sequences.

Finding the best alignment with dynamic programming A group of algorithms calculate the best score and alignment in the order of steps. These dynamic programming algorithms were first developed for protein sequence comparison by Needleman and Wunsch (J Mol Biol 48, 443, 1970).

Pairwise and multiple sequence alignments can be global or local • Globlal: the whole sequence is aligned • Local : only fragments of the sequence are aligned

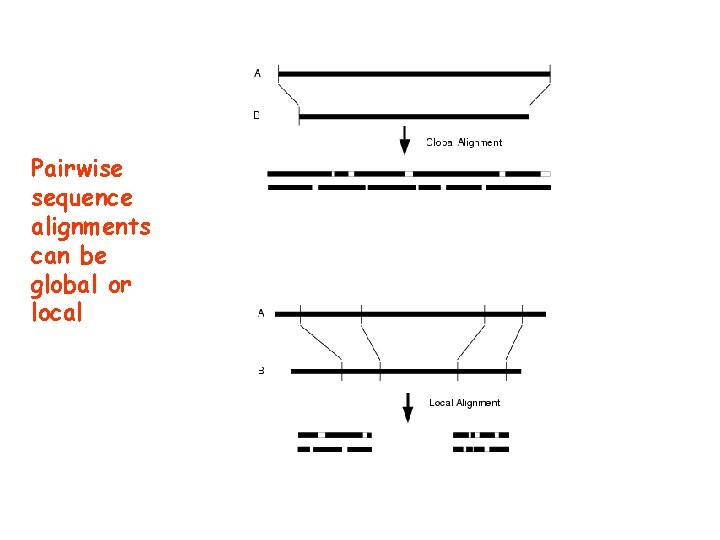
Pairwise sequence alignments can be global or local

DATABASE SCANNING • Word or K-tuple methods (FAST, BLAST)

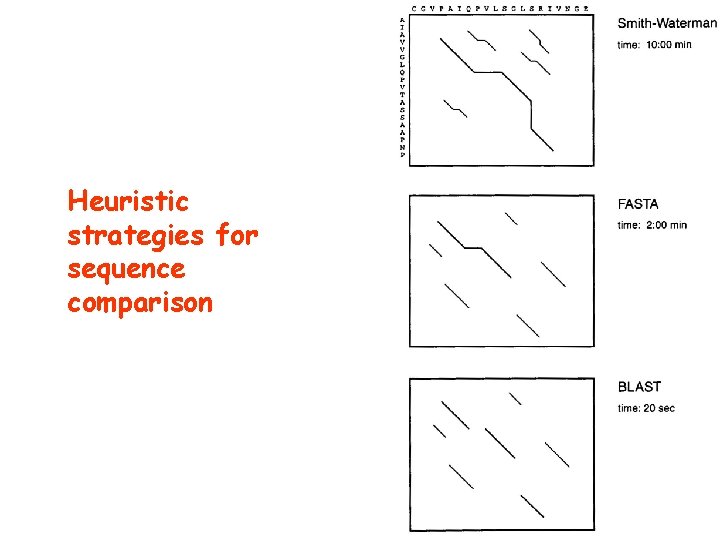
Heuristic strategies for sequence comparison

Sequence similarity with FASTA

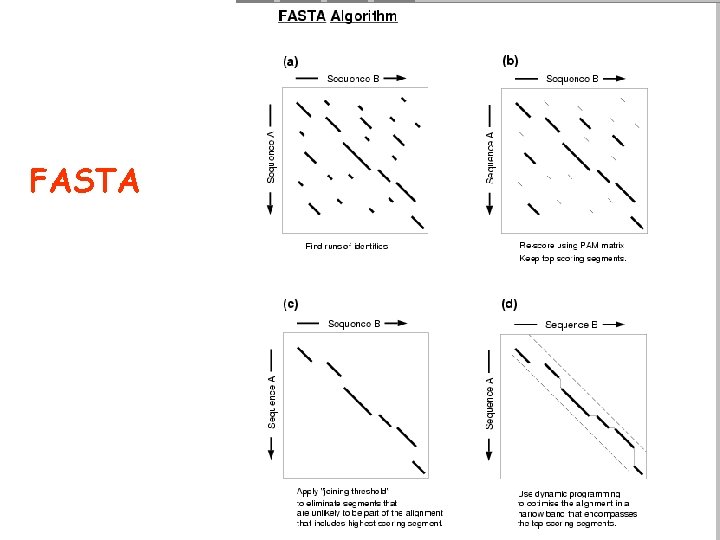
FASTA

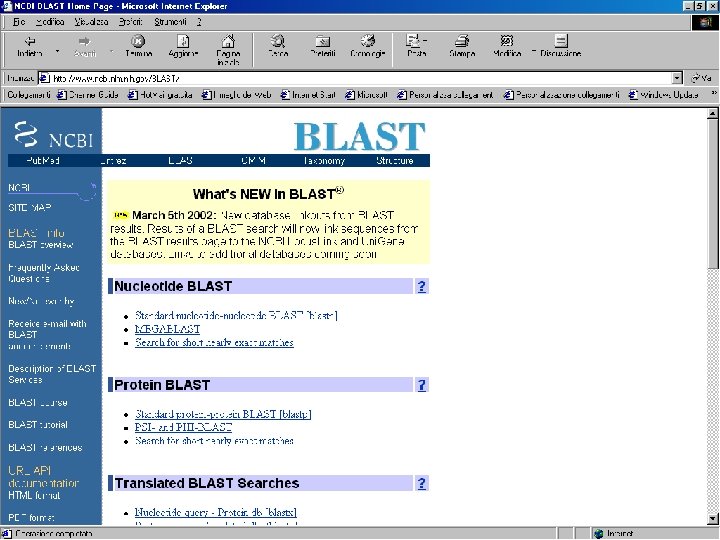
Sequence similarity with BLAST (Basic Local Alignment Search Tool)

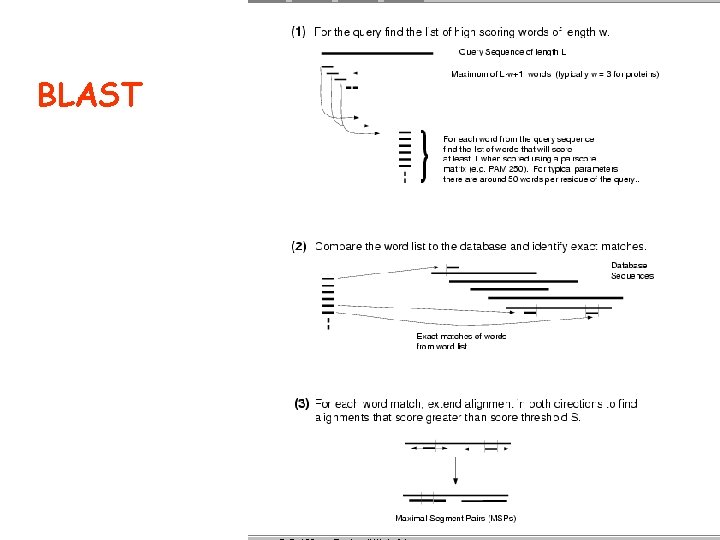
BLAST

PAM 250

Blosum 50 A R N D C Q E G H I L K M F P S T W Y V A 5 -2 -1 -1 -1 0 -2 -1 -1 -3 -1 1 0 -3 -2 0 R -2 7 -1 -2 -4 1 0 -3 0 -4 -3 3 -2 -3 -3 -1 -1 -3 N -1 -1 7 2 -2 0 0 0 1 -3 -4 0 -2 -4 -2 1 0 -4 -2 -3 D -2 -2 2 8 -4 0 2 -1 -1 -4 -4 -1 -4 -5 -1 0 -1 -5 -3 -4 C -1 -4 -2 -4 13 -3 -3 -2 -2 -4 -1 -1 -5 -3 -1 Q -1 1 0 0 -3 7 2 -2 1 -3 -2 2 0 -4 -1 0 -1 -1 -1 -3 E -1 0 0 2 -3 2 6 -3 0 -4 -3 1 -2 -3 -1 -1 -1 -3 -2 -3 G 0 -3 0 -1 -3 -2 -3 8 -2 -4 -4 -2 -3 -4 -2 0 -2 -3 -3 -4 H -2 0 1 -1 -3 1 0 -2 10 -4 -3 0 -1 -1 -2 -3 2 -4 I -1 -4 -3 -4 -2 -3 -4 -4 -4 5 2 -3 2 0 -3 -3 -1 4 L -2 -3 -4 -4 -2 -2 -3 -4 -3 2 5 -3 3 1 -4 -3 -1 -2 -1 1 K -1 3 0 -1 -3 2 1 -2 0 -3 -3 6 -2 -4 -1 0 -1 -3 -2 -3 M -1 -2 -2 -4 -2 0 -2 -3 -1 2 3 -2 7 0 -3 -2 -1 -1 0 1 F -3 -3 -4 -5 -2 -4 -3 -4 -1 0 1 -4 0 8 -4 -3 -2 1 4 -1 P -1 -3 -2 -1 -4 -1 -1 -2 -2 -3 -4 -1 -3 -4 10 -1 -1 -4 -3 -3 S 1 -1 1 0 -1 -3 -3 0 -2 -3 -1 5 2 -4 -2 -2 T 0 -1 -1 -2 -2 -1 -1 -2 -1 2 5 -3 -2 0 W -3 -3 -4 -5 -5 -1 -3 -3 -2 -3 -1 1 -4 -4 -3 15 2 -3 Y -2 -1 -2 -3 -3 -1 -2 -3 2 -1 -1 -2 0 4 -3 -2 -2 2 8 -1 V 0 -3 -3 -4 -1 -3 -3 -4 -4 4 1 -3 1 -1 -3 -2 0 -3 -1 5

BLOSUM 62

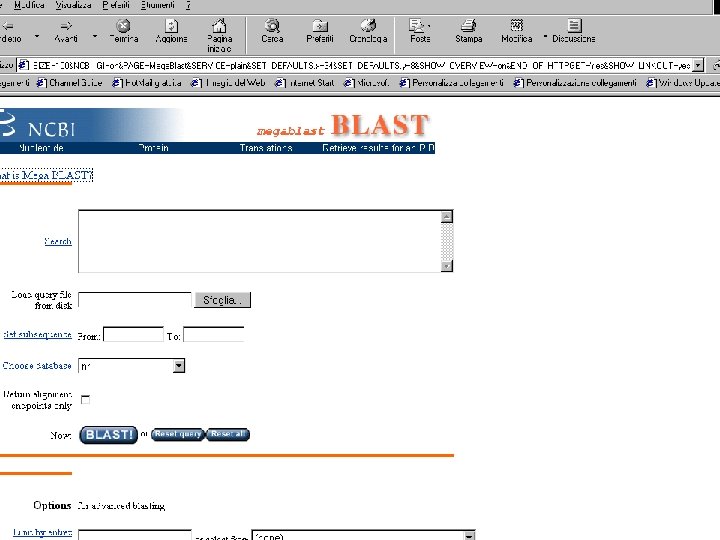
MEGABLAST Search Mega BLAST uses the greedy algorithm for nucleotide sequence alignment search. This program is optimized for aligning sequences that differ slightly as a result of sequencing or other similar "errors". When larger word size is used (see explanation below), it is up to 10 times faster than more common sequence similarity programs. Mega BLAST is also able to efficiently handle much longer DNA sequences than the blastn program of traditional BLAST algorithm.

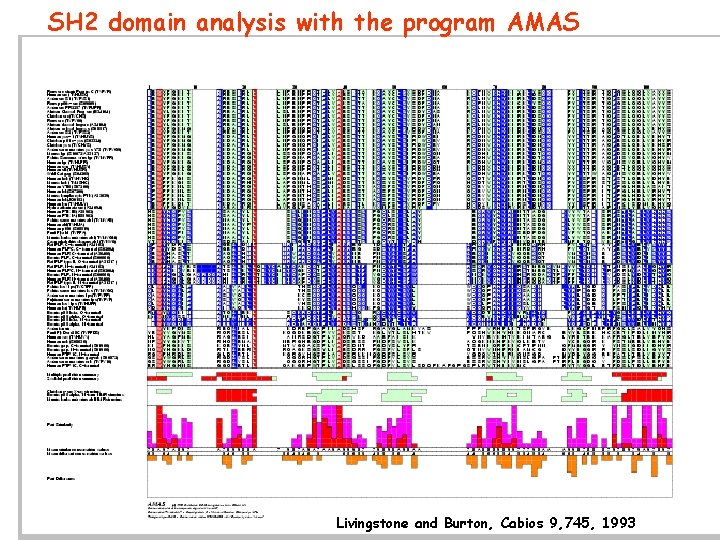
SH 2 domain analysis with the program AMAS Livingstone and Burton, Cabios 9, 745, 1993

Multiple Alignment How to build a sequence profile

The design of PSI-BLAST (1) PSI-BLAST takes as an input a single protein sequence and compares it to a protein database, using the gapped BLAST program (2) The program constructs a multiple alignment, and then a profile, from any significant local alignments found. The original query sequence serves as a template for the multiple alignment and profile, whose lengths are identical to that of the query. Different numbers of sequences can be aligned in different template positions (3) The profile is compared to the protein database, again seeking local alignments. After a few minor modifications, the BLAST algorithm can be used for this directly. (4) PSI-BLAST estimates the statistical significance of the local alignments found. Because profile substitution scores are constructed to a fixed scale, and gap scores remain independent of position, the statistical theory and parameters for gapped BLAST alignments remain applicable to profile alignments. (5) Finally, PSI-BLAST iterates, by returning to step (2), an arbitrary number of times or until convergence.

http: //helix. biology. mcmaster. ca/721/distance/node 9. html

http: //barton. ebi. ac. uk/papers/rev 93_/ tableofcontents 3_1. html

Sequence Alignment: Statistics Rita Casadio

The statistics of global sequence comparison

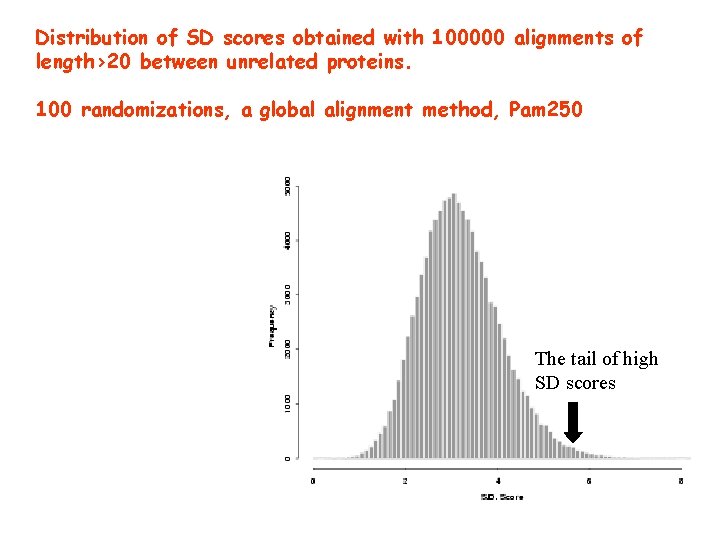
Distribution of SD scores obtained with 100000 alignments of length>20 between unrelated proteins. 100 randomizations, a global alignment method, Pam 250 The tail of high SD scores

The Z score: Z=(Xs-Xt)/ s Xs=average of distribution scores with random sequences Xt=average of distribution score with real sequences s=SD of distribution scores with random sequences Accuracy of the alignment: Z<3 not significant 3<Z<6 putatively significant 6<Z<10 possibly significant Z>10 significant

How reliable is the Z score? The Z score of this local alignment is 7. 5 over 54 residues, identity is 25. 9%. The sequences are of completely different secondary structure Citrate synthase (2 cts) vs transthyritin (2 paba)

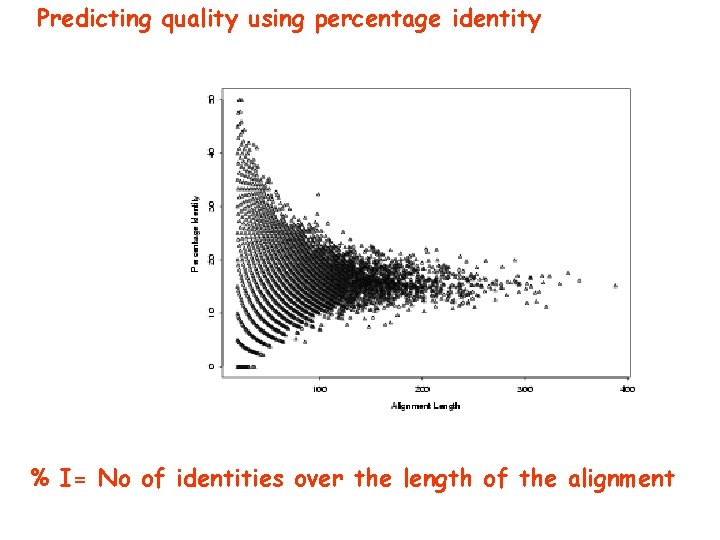
Predicting quality using percentage identity % I= No of identities over the length of the alignment

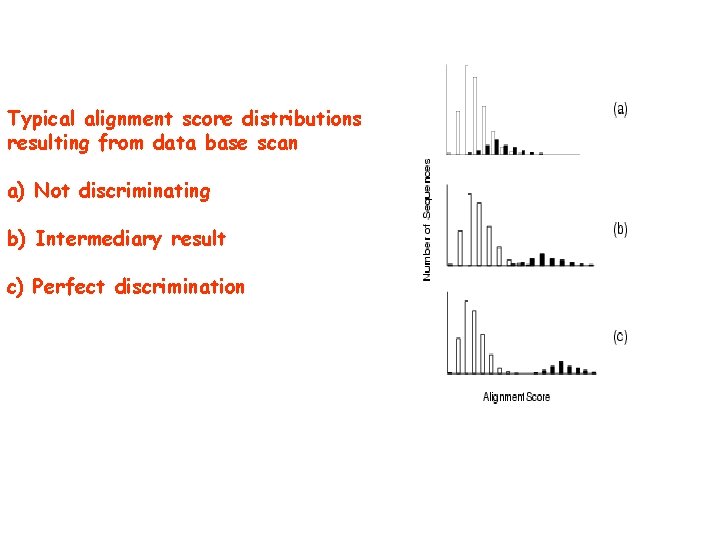
Typical alignment score distributions resulting from data base scan a) Not discriminating b) Intermediary result c) Perfect discrimination

The statistics of global sequence comparison To assess whether a given alignment constitutes evidence for homology, it helps to know how strong an alignment can be expected from chance alone. In this context, "chance" can mean the comparison of (i) real but nonhomologous sequences; (ii) real sequences that are shuffled to preserve compositional properties or (iii) sequences that are generated randomly based upon a DNA or protein sequence model. Analytic statistical results invariably use the last of these definitions of chance, while empirical results based on simulation and curve-fitting may use any of the definitions.

The P-value The probability that a variate would assume a value greater than or equal to the observed value strictly by chance P(z>zo) It is possible to express the score of interest in terms of standard deviations from the mean; it is a mistake to assume that the relevant distribution is normal and convert the Z-value into a P-value; the tail behavior of global alignment scores is unknown. The most one can say reliably is that if 100 random alignments have score inferior to the alignment of interest, the P-value in question is likely less than 0. 01.

The statistics of local sequence comparison

A local alignment without gaps consists simply of a pair of equal length segments, one from each of the two sequences being compared. The scores of segment pairs can not be improved by extension or trimming. These are called high-scoring segment pairs or HSPs. The maximum of a large number of independent idendically distributed random variables tends to an extreme value distribution.

The maximum of a large number of independent idendically distributed random variables tends to an extreme value distribution P(S<x)=exp[-exp(-x)] P(S>=x)= 1 - exp[-exp(-x)]

E value In the limit of sufficiently large sequence lengths m and n, the statistics of HSP scores are characterized by two parameters, K and lambda. Most simply, the expected number of HSPs with score at least S is given by the E-value for the score S: E=Kmn exp(- S) The parameters K and lambda can be thought of simply as natural scales for the search space size and the scoring system respectively. Bit scores: S’= ( S-ln. K)/ln 2 The E-value corresponding to a given bit score is: E=mn 2–S’

P-value: The chance of finding zero HSPs with score >=S is exp(-E), so the probability of finding at least one such HSP is P=1 -exp(-E) This is the P-value associated with the score S.

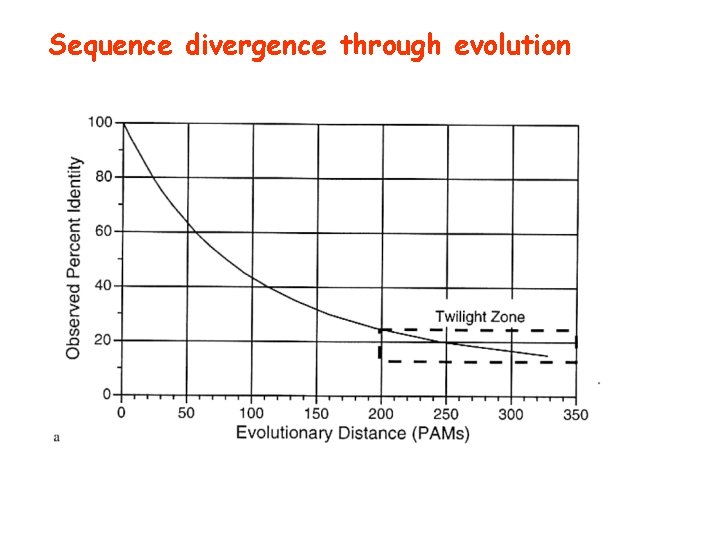
Sequence divergence through evolution