Bioinformatics Algorithms and Data Structures Chapter 17 4

Bioinformatics Algorithms and Data Structures Chapter 17. 4 -6: Strings and Evolutionary Trees Lecturer: Dr. Rose Slides by: Dr. Rose April 17, 2003 UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem Centrality Four related tree problems: • • • 1. Ultrametric 2. Additive 3. Binary perfect phylogeny 4. Tree compatibility All can be solved as ultrametric tree problems. Recall tree compatibility reduces to perfect phylogeny. Now we reduce additive tree & (binary) perfect phylogeny problems to the ultrametric tree problem. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees • • • Goal: reduce additive tree problem to ultrametric problem Complexity: O(n 2) reduction Approach: create a matrix D that is ultrametric D is additive. We will start by describing a reduction that involves a tree T for D and T for D. We will then describe a direct reduction of D to D. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees • • • Assume that D is additive. Assume that we know of an additive tree T for D Assume that each of the n taxa in D labels a leaf of T. Idea: label the nodes of T to create an ultrametric tree T. Q: How can we do this? UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees A: we will do the following: – – • • Select one node as the root Stretch the leaf edges so that they are equidistant from the root. Let v be the row of D containing the largest entry. Let mv denote the value of this entry. Select node v as the root of T. This creates a directed tree. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

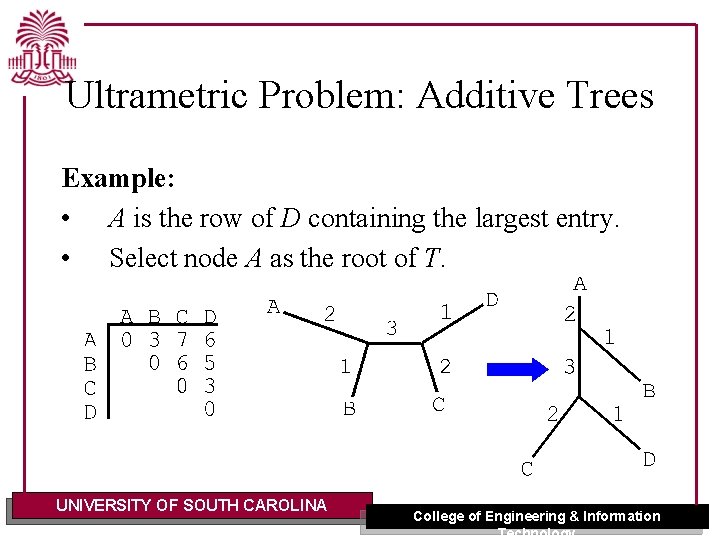
Ultrametric Problem: Additive Trees Example: • A is the row of D containing the largest entry. • Select node A as the root of T. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

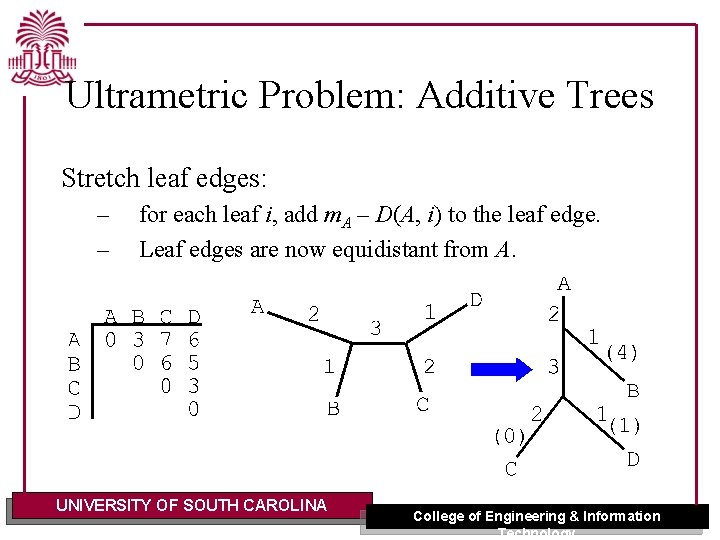
Ultrametric Problem: Additive Trees Stretch leaf edges: – – for each leaf i, add m. A – D(A, i) to the leaf edge. Leaf edges are now equidistant from A. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees The resulting tree T is: – – – a rooted edge-weighted tree distance mv from root to every leaf each internal node is equidistant to leaves in its subtree. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Since each internal node is equidistant to the leaves in its subtree: • Label each internal node by this unique distance. • These labels can be used to define an ultrametric matrix D. • D (i, j) is the label at the least common ancestor of leaves i and j in T. Q: How can we go directly from matrix D to matrix D without involving T and T ? UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Consider leaves i & j in T: – – – Let node w be their least common ancestor Let x be the distance from the root v to w. Let y be the distance from node w to leaf i. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

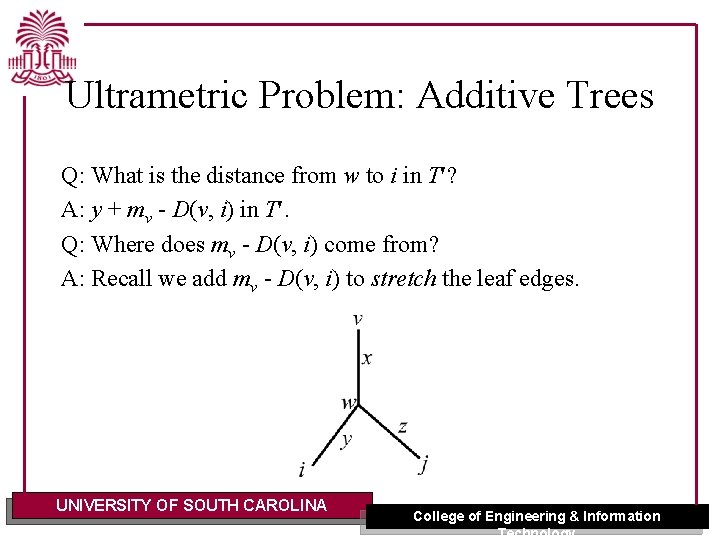
Ultrametric Problem: Additive Trees Q: What is the distance from w to i in T ? A: y + mv - D(v, i) in T. Q: Where does mv - D(v, i) come from? A: Recall we add mv - D(v, i) to stretch the leaf edges. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Gusfield presents the following lemma: Without knowing T or T´ explicitly, we can deduce that D´(i, j) = mv + (D(i, j) - D(v, i) - D(v, j))/2 Q: Is this equation correct? D´(i, j) = mv + ((y + z) - (x + y) - (x + z))/2 ? D´(i, j) = mv + -2 x/2 ? Should it instead be: D´(i, j) = 2 mv + D(i, j) - D(v, i) - D(v, j)? i. e. , D´(i, j) = 2 mv - 2 x? Probably, but it is not necessary for the reduction (slide 9) UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees This brings us to the following Theorem: If D is an additive matrix, then D´ is ultrametric, where D´(i, j) = mv + (D(i, j) - D(v, i) - D(v, j))/2 Proof. We’ve shown that: D´(i, j) = y + mv - D(v, i) y = D(v, i) – x x = (D(v, i) + D(v, j) - D(i, j))/2 Putting it altogether establishes the equation in theorem. D´ satisfies the ultrametric requirement. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Q: What is the value of y? A: y = D(v, i) - x. Q: What is the value of x in terms of values in D? A: x = (D(v, i) + D(v, j) - D(i, j))/2 UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees So: D additive D´ ultrametric By contraposition: D´ ultrametric D additive Q: does D´ ultrametric D additive? A: Theorem: D´ ultrametric D additive Proof. (constructive) • Let T´´ be the ultrametric tree for D´ • Assign weights to edges of T´´ – – Note: the sum of edges from a leaf to an ancestor must match the ancestor’s label. For each edge (p, q), assign the weight |p-q| UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees • Assign weights to edges of T´´ continued – – Note the path distance between leaves (i, j) is twice the value labeling the least common ancestor Hence, 2 D´(i, j) = 2 mv + D(i, j) - D(v, i) - D(v, j) Now shrink the edge into each leaf i by mv - D(v, i) The path from leaf i to leaf j is now D(i, j) The result is an additive tree for matrix D from D´’s ultrametric tree. Putting all of this together results in a method for contructing and additive tree for an additive matrix. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Additive Tree Algorithm – – – Create matrix D´ from D. Create ultrametric tree T´´ from D´ Create T from T´´ • • Label edge (p, q) with the value |p-q| For each leaf i, shrink the leaf edge by mv - D(v, i) Note: no step takes more than O(n 2) time. Thm. An additive tree for an additive matrix can be constructed in O(n 2) time. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Additive Trees Example: Given D, first find D´ Recall: D´(i, j) = mv + (D(i, j) - D(v, i) - D(v, j))/2 UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

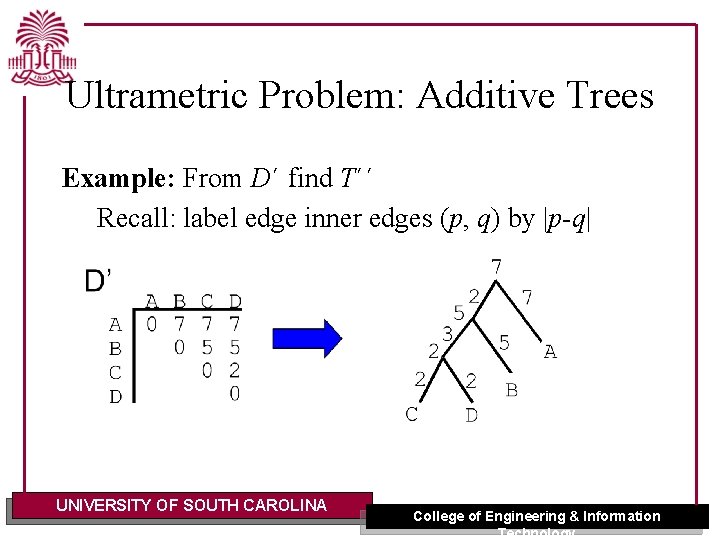
Ultrametric Problem: Additive Trees Example: From D´ find T´´ Recall: label edge inner edges (p, q) by |p-q| UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

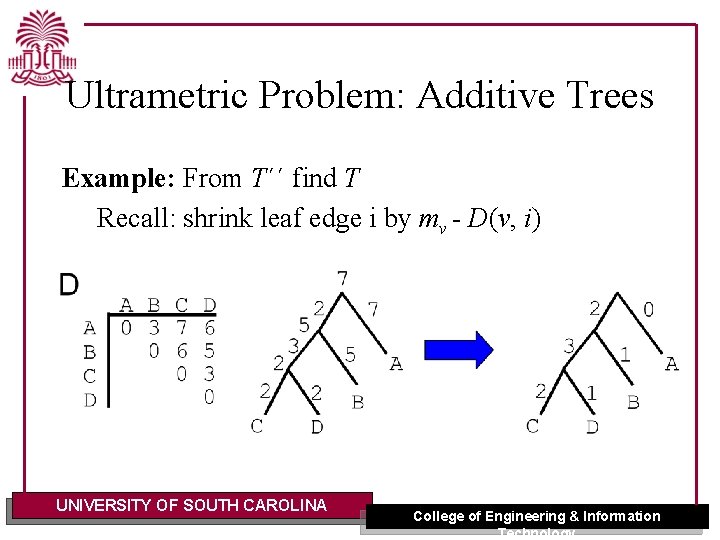
Ultrametric Problem: Additive Trees Example: From T´´ find T Recall: shrink leaf edge i by mv - D(v, i) UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

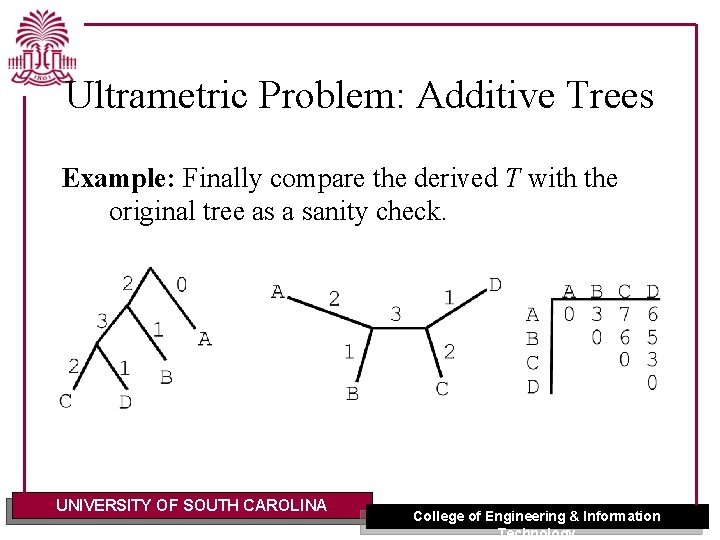
Ultrametric Problem: Additive Trees Example: Finally compare the derived T with the original tree as a sanity check. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Perfect Phylogeny We now recast perfect phylogeny in terms of an ultrametric tree problem. Defn. DM – the n by n matrix of shared characters More formally: Given the n by m character matrix M, define the n by n matrix DM: for each pair of objects, set DM(p, q) to be the number of characters that p and q both possess. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Perfect Phylogeny Lemma: If M has a perfect phylogeny, then DM is a min-ultrametric matrix. Proof: convert M’s perfect phylogeny T to a minultrametric tree for DM – – – Let T be the perfect phylogeny for M. Label T’s root be zero. Traverse T from top to bottom, for each node v: • • • Let pv be the number labeling node v’s parent. Let ev be the # of characters labeling the edge into v. Label node v with the sum pv + ev UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Perfect Phylogeny – The label of node v is the number of characters common to all leaves in the subtree rooted at v. – if v is the immediate parent of leaves p and q, then the label of v is DM(p, q) – The numbers labeling nodes on any path from the root are strictly increasing. q The result is an ultrametric tree for matrix DM. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Perfect Phylogeny Algorithm: perfect phylogeny via ultrametrics: 1. Create matrix DM from M. 2. Attempt to create a min-ultrametric tree T´ from DM. If not possible, then M has no perfect phylogeny. 3. If T´ was successfully created in step 2: • • • Attempt to label its edges with the m characters of M. If not possible, then M has no perfect phylogeny. O/w the modified T´ is the perfect phylogeny T. Note: T´ may be min-ultrametric but M may not have a perfect phylogeny, hence the check in step 3 UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Ultrametric Problem: Perfect Phylogeny Final notes on the centrality ultrametric problem. We can see that the following problems: 1. perfect phylogeny 2. tree compatibility can be cast as ultrametric problems. This is not an efficient way to address these problems. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony Maximum parsimony: • • Perfect phylogeny is a special instance Can be viewed as a Steiner tree problem on a hypercube Presentation Approach: • • • Introduce Steiner trees Hypercube graphs Maximum parsimony as a Steiner tree problem UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony Definitions: Let N be a set of nodes Let E be a set undirected edges with non-negative weight Let G = (N, E) be an undirected graph Let X N be a subset of nodes. A Steiner tree ST for X is any connected subtree of G that contains all nodes of X and possibly nodes in N-X. Weighted Steiner Tree Problem: Given G and X, find the Steiner tree of minimum total weight. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony More Definitions: A hypercube of dimension d is an undirected graph with 2 d nodes, labeled 0. . 2 d-1. Adjacent nodes differ in only one label bit position. The weighted Steiner tree problem on hypercubes: G must be a hypercube. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony More Definitions: Maximum Parsimony: Occam’s razor applied to phylogenetic reconstruction. A preference for trees requiring fewer evolutionary events to explain data. Gusfield’s definition: The Maximum Parsimony problem is the unweighted Steiner tree problem on a d-dimensional hypercube. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony More about the hypercube formulation of MP: – – – The X input taxa are described as d-length binary vectors. Recall: adjacent nodes differ in only one label bit position. Correspondingly, taxa that differ by a single mutation will be adjacent. Steiner tree of X nodes and l edges iff a corresponding phylogenetic tree that entails l character-state mutations. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Steiner interpretation of Perfect Phylogeny Define a nontrivial binary character to be a character contained by some taxa but not all. Consider an MP dataset of d nontrivial binary characters Q: what is the minimal number of mutations in the MP tree? A: at least d. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Steiner interpretation of Perfect Phylogeny Q: What is the relation to binary perfect phylogeny? A: the binary perfect phylogeny problem is equivalent to asking if there is an MP solution with a cost of exactly d. Q: What about generalized perfect phylogeny? A: It’s similar. The lower bound must reflect: – – the number of character states in the input taxa. a character having r states in the input taxa is allowed only r-1 transitions. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Steiner interpretation of Perfect Phylogeny Complexity: • No known efficient solution for Steiner tree problem on unweighted graphs. • Polynomial time solution for generalized perfect phylogeny problem when r is fixed. this particular Steiner tree problem can be answer in polynomial time. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Steiner interpretation of Perfect Phylogeny MP approximations: – – – The weighted Steiner tree problem on hypercubes is NP-hard. There is an approximate method with an error bound of a factor of 11/6. Also MST can be used to find a Steiner tree with weight less than twice the optimal Steiner tree. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Phylogenetic Alignment Recall: • • phylogenetic alignment was discussed in section 14. 8 The focus was on deriving a multiple alignment enlightened by evolutionary history. The tree focused emphasis on specific alignment groupings Internal node sequences were a secondary artifact UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Phylogenetic Alignment Phylogenetic alignment as a parsimony problem: In contrast: • we are now interested in the internal sequences • These sequences are waypoints in the evoutionary trajectory leading to the extant taxa • phylogenetic alignment is thus a parsimony problem UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Phylogenetic Alignment Hypothesis: optimal phylogenetic alignment describes evolutionary history. Assumptions: – – Edit distance realistically models evolutionary distance Globally optimal phylogenetic alignment captures essence of the evolutionary process We will look at minimum mutation, a variant of phylogenetic alignment UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Defn. minimum mutation problem – variant of phylogenetic alignment problem. Input comprised of: 1. Tree 2. Strings labeling the leaves 3. A multiple alignment of those strings UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Q: If you are given the tree and the multiple alignment, what is left to compute? A: the mutations that accounts for the input data. These mutations should be: 1. minimum sequence of site mutations that is 2. compatible with the given tree and 3. the given multiple alignment. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Q: How is the input data used to determine the minimum sequence of mutations? 1. The multiple alignment associates each amino acid with a specific position. 2. The evolutionary history of the sequences is then treated as a combined but independent evolutionary history of each position. 3. The tree guides the order of mutations for each position. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Assumptions: – – Each column of the alignment can be solved separately The strings labeling inner nodes adhere to the same alignment The problem reduces to a computation at a single position. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Minimum mutation for a single position: Input: 1. rooted tree with n nodes 2. Each leaf is labeled by a single character Output: 1. Each interior node is labeled by a single character 2. The labeling minimizes the number of edges between nodes with different labels. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Algorithmic approach: Dynamic Programming • • • Let Tv denote the subtree rooted at node v Let C(v) be the cost of the optimal solution for Tv Let C(v, x) be the cost when v must be labeled by x Let vi denote the ith child of node v Base case: for each leaf specify C(v) & C(v, x) x S. • • C(v) = 0 & C(v, x) = 0 if leaf v is labeled by x. C(v, x) = if leaf v is not labeled by x. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem When v is an internal node: The recurrence relations start from the base cases. • • Bottom up from leaves Backtracking is used to after all C(v, x) computed to extract the solution. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Backtracking process: • • • The root is labeled by the character x s. t. C(r) = C(r, x) The traversal is then top-down If v is labeled x, then vi is labeled: • • character x if C(vi) + 1 > C(vi, x) o/w character y such that C(vi) = C(vi, y) UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Let’s evaluate an example: C(v) = 0 & C(v, x) = 0 if leaf v is labeled by x, o/w C(v, x) = if leaf v is not labeled by x. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Fitch-Hartigan minimum mutation problem Time complexity: Bottom-up portion – Let s = |S| – Each node is evaluate wrt each x S. – For n nodes this gives O(ns) The backtracking portion is O(n) Overall O(ns) UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Maximum Parsimony • • Most widely used tree building algorithm Differs from distance-based algorithms: – – Does not actually build trees from distances Parsimony is used to compute the cost of a tree A search strategy is used to search through all topologies Goal: find the tree topology with the overall minimum cost UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Traditional Parsimony Algorithm: Traditional parsimony [Fitch 1971] • Goal: count the number of substitutions at a site. • Method: recursion, keeping track of – – C, the current cost Rk, the residues at k, the current node UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Traditional Parsimony Algorithm: Traditional parsimony [Fitch 1971] C = 0, k = root / initialize the cost and TP(k) { If k is a leaf then return xk Rleft = TP( k. left) Rright = TP(k. right) if Rleft Rright return Rleft Rright else { C = C +1 return Rleft Rright }} UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Traditional Parsimony Let’s evaluate an example: if Rleft Rright return Rleft Rright else C = C +1, return Rleft Rright UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Traditional Parsimony There is a traceback procedure for finding ancestral assignments. Q: How do you think the traceback works? A: Start from the root: 1. Pick a residue 2. Pick the same residue for each child set if possible 3. If a child set does not contain the parent’s residue, randomly select a residue from its set. UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology

Traditional Parsimony Let’s perform the traceback on our example: UNIVERSITY OF SOUTH CAROLINA College of Engineering & Information Technology