Bioinformatics 4 Sequence Analysis Sequence Similarity and Homology

Bioinformatics (4) Sequence Analysis
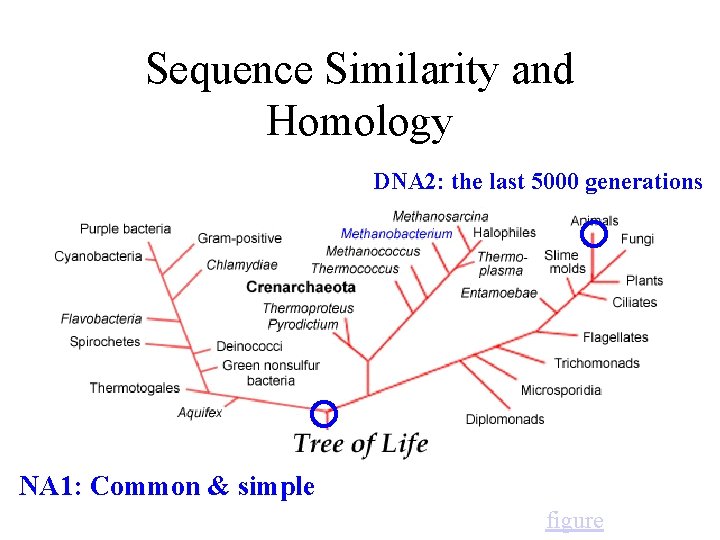
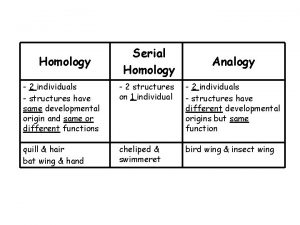
Sequence Similarity and Homology DNA 2: the last 5000 generations NA 1: Common & simple figure

Alignments & Scores Global (e. g. haplotype) ACCACACA : : xx: : x: ACACCATA Score= 5(+1) + 3(-1) = 2 Local (motif) ACCACACA : : ACACCATA Score= 4(+1) = 4 Suffix (shotgun assembly) ACCACACA : : : ACACCATA Score= 3(+1) =3

"Hardness" of (multi-) sequence alignment Align 2 sequences of length N allowing gaps. ACCAC-ACA : : x: x: AC-ACCATA , ACCACACA : xxxxxx: A-----CACCATA , etc. 2 N gap positions, gap lengths of 0 to N each: A naïve algorithm might scale by O(N 2 N). For N= 3 x 109 this is rather large. Now, what about k>2 sequences? or rearrangements other than gaps?

Increasingly complex (accurate) searches Exact (stringsearch) Regular expression (Prosite. Search) CGCG CGN{0 -9}CG = CGAACG Substitution matrix (Blast. N) Profile matrix (PSI-blast) CGCG ~= CACG CGc(g/a) ~ = CACG Gaps (Gap-Blast) Dynamic Programming (NW, SM) CGCG ~= CGAACG CGCG ~= CAGACG

Comparisons of homology scores Pearson WR Protein Sci 1995 Jun; 4(6): 1145 -60 Comparison of methods for searching protein sequence databases. Methods Enzymol 1996; 266: 227 -58 Effective protein sequence comparison. Algorithm: FASTA, Blastp, Blitz Substitution matrix: PAM 120, PAM 250, BLOSUM 62 Database: PIR, SWISS-PROT, Gen. Pept

Scoring matrix based on large set of distantly related blocks: Blosum 62

Scoring Functions and Alignments • Scoring function: – (match) = +1; or substitution matrix – (mismatch) = -1; " – (indel) = -2; – (other) = 0. • Alignment score: sum of columns. • Optimal alignment: maximum score.

Calculating Alignment Scores

What is dynamic programming? A dynamic programming algorithm solves every subsubproblems just once and then saves its answer in a table, avoiding the work of recomputing the answer every time the subsubproblem is encountered. -- Cormen et al. "Introduction to Algorithms", The MIT Press.
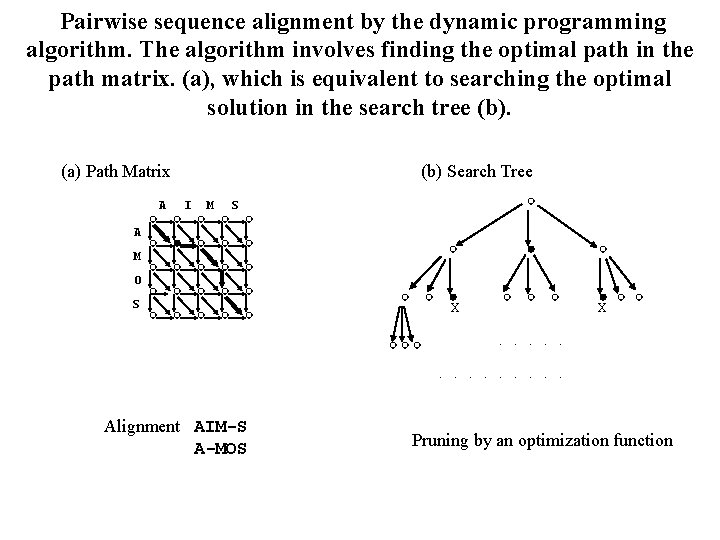
Pairwise sequence alignment by the dynamic programming algorithm. The algorithm involves finding the optimal path in the path matrix. (a), which is equivalent to searching the optimal solution in the search tree (b). (a) Path Matrix A (b) Search Tree I M S A M O S X . Alignment AIM-S A-MOS . X . . . Pruning by an optimization function
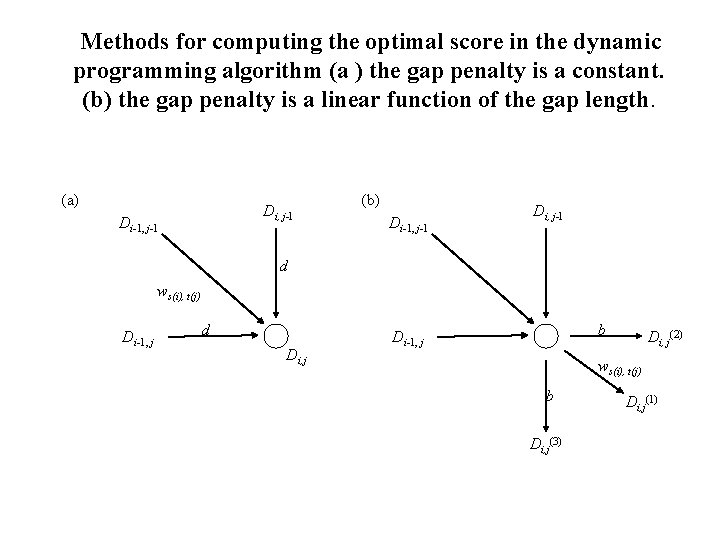
Methods for computing the optimal score in the dynamic programming algorithm (a ) the gap penalty is a constant. (b) the gap penalty is a linear function of the gap length. (a) Di, j-l Di-1, j-1 (b) Di-1, j-1 Di, j-l d ws(i), t(j) Di-1, j d Di, j b Di-1, j Di, j(2) ws(i), t(j) b Di, j(3) Di, j(1)

Recursion of Optimal Global Alignments
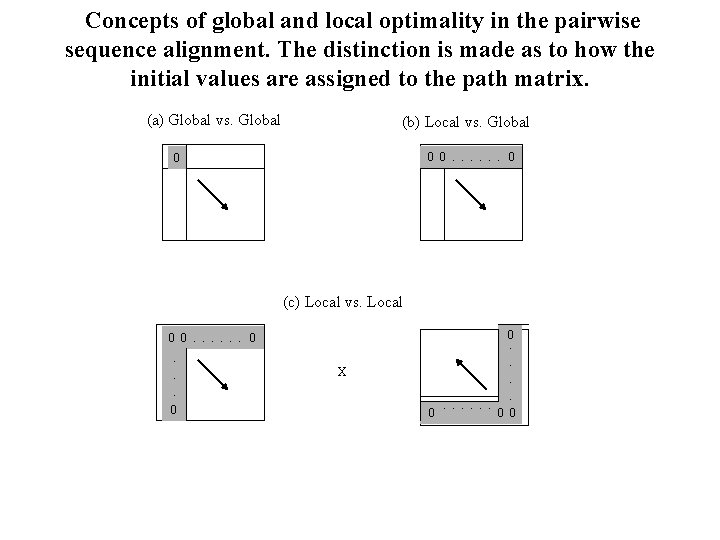
Concepts of global and local optimality in the pairwise sequence alignment. The distinction is made as to how the initial values are assigned to the path matrix. (a) Global vs. Global (b) Local vs. Global 0 0. . . 0 0 (c) Local vs. Local X 0 0. 0. . . 0

Recursion of Optimal Local Alignments
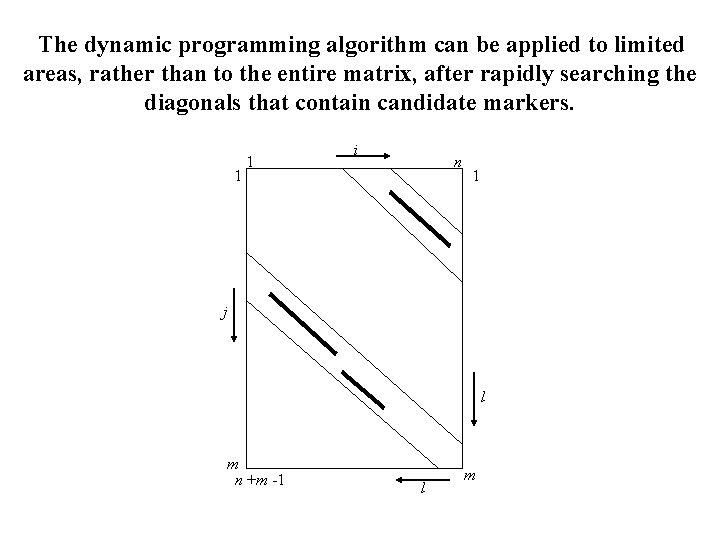
The dynamic programming algorithm can be applied to limited areas, rather than to the entire matrix, after rapidly searching the diagonals that contain candidate markers. 1 1 i n 1 j l m n +m -1 l m
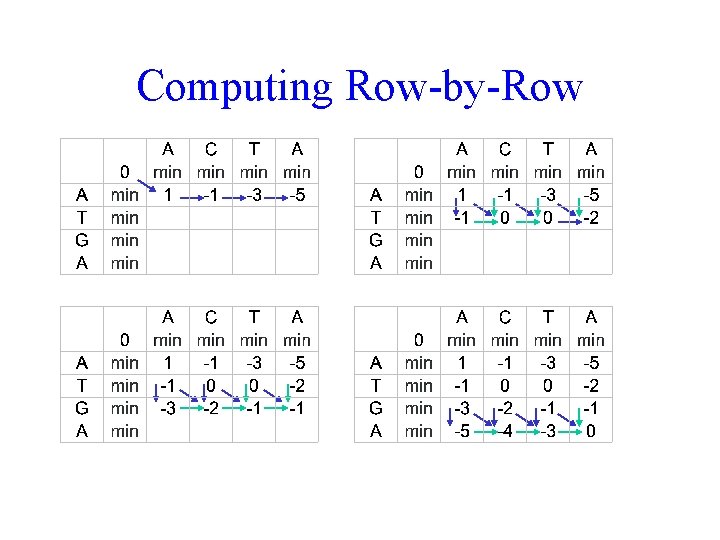
Computing Row-by-Row

Traceback Optimal Global Alignment
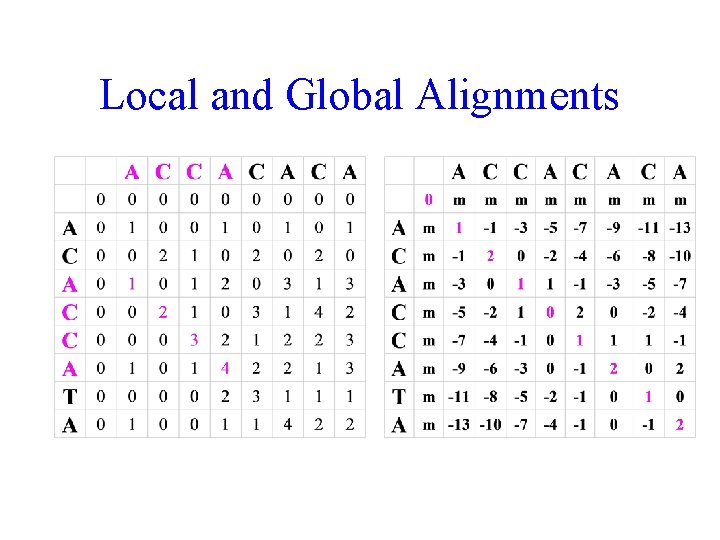
Local and Global Alignments

Time and Space Complexity of Computing Alignments
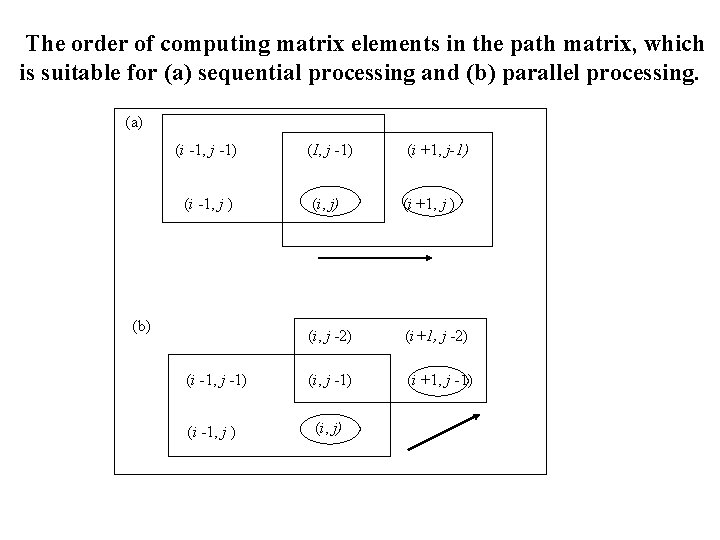
The order of computing matrix elements in the path matrix, which is suitable for (a) sequential processing and (b) parallel processing. (a) (i -1, j -1) (I, j -1) (i +1, j-1) (i -1, j ) (i, j) (i +1, j ) (i, j -2) (i+1, j -2) (i, j -1) (i +1, j -1) (b) (i -1, j -1) (i -1, j ) (i, j)

Time and Space Problems • Comparing two one-megabase genomes. • Space: – An entry: 4 bytes; – Table: 4 * 10^6 = 4 G bytes memory. • Time: – 1000 MHz CPU: 1 M entries/second; – 10^12 entries: 1 M seconds = 10 days.
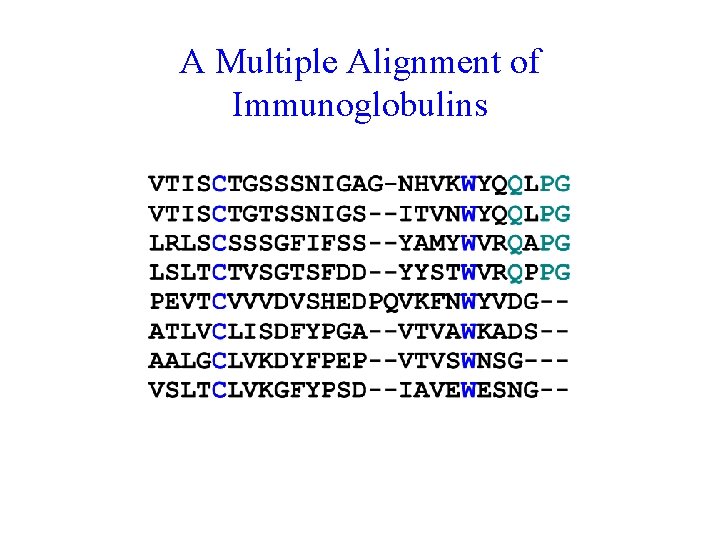
A Multiple Alignment of Immunoglobulins
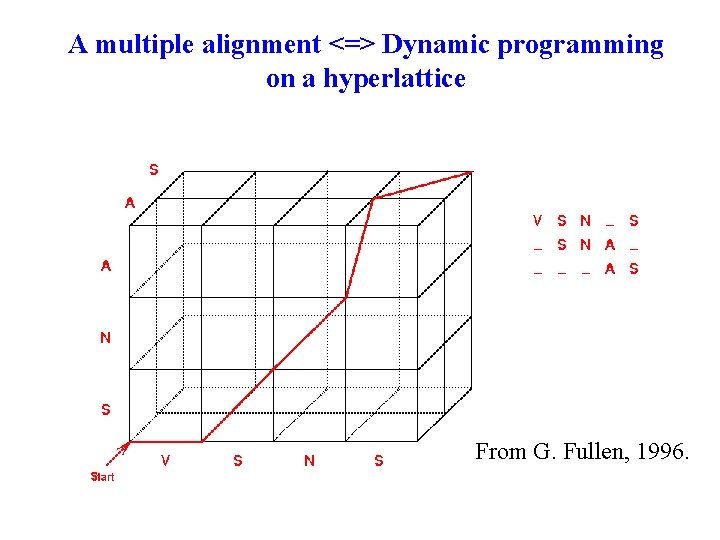
A multiple alignment <=> Dynamic programming on a hyperlattice From G. Fullen, 1996.
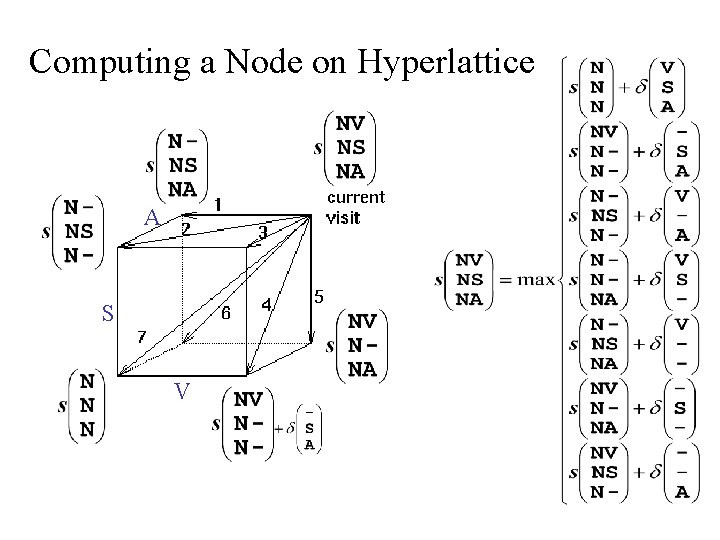
Computing a Node on Hyperlattice A S V
- Slides: 25