BINOMIAL THEOREM BINOMIAL THEOREM INTRODUCTION BINOMIAL THEOREM BINOMIAL
BINOMIAL THEOREM

BINOMIAL THEOREM INTRODUCTION

BINOMIAL THEOREM BINOMIAL EXPRESSION An expression consisting of two terms is known as binomial expression. For example (x + a) is a binomial expression.

BINOMIAL THEOREM Consider (x + a)1 = x + a (x + a)2 = x 2 + 2 xa + a 2 (x + a)3 = x 3 + 3 x 2 a + 3 xa 2 + a 3 (x + a)4 = x 4 + 4 x 3 a + 6 x 2 a 2 + 4 xa 3 +a 4 Ø The right hand side expressions in the above equations are known as binomial expansions. Ø The coefficients in the above expansions are called binomial coefficients.

BINOMIAL THEOREM Ø These binomial coefficients can be expressed in the form of a triangle. This triangular form is called Pascal triangle. Pascal Triangle 1 1 2 1 1 3 3 1 1 4 6 4 1

BINOMIAL THEOREM FOR POSITIVE INTEGRAL INDEX Theorem: If n is a positive integer then (x + a)n = n. C 0 xn + n. C 1 xn-1 a + n. C 2 xn-2 a 2 +……+ n. Crxn-r ar + …. + n. Cn an. Proof Let S(n) be the statement that (x + a)n = n. C 0 xn + n. C 1 xn-1 a + n. C 2 xn-2 a 2 +……+ n. Crxn-r ar + …. + n. Cn an. If n=1, then L. H. S = (x + a)1 = x + a

BINOMIAL THEOREM R. H. S = 1 C 0 x 1 + 1 C 1 x 1 -1 a = x + a Assume that S(k) is true i. e. (x+a)k = k. C 0 xk + k. C 1 xk-1 a + k. C 2 xk-2 a 2+…. + k. Cr xk-r ar + …. +k. Ck ak. Now (x + a)k+1 = (x + a)k
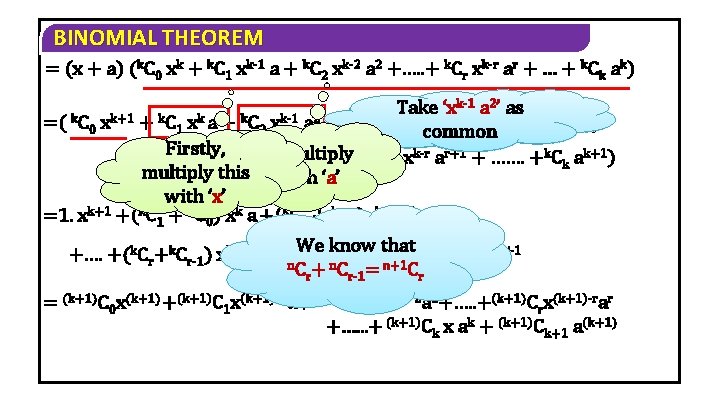
BINOMIAL THEOREM = (x + a) (k. C 0 xk + k. C 1 xk-1 a + k. C 2 xk-2 a 2 +…. . + k. Cr xk-r ar + … + k. Ck ak) k-1 2 as k a’ Take ‘x a ’ as k Take ‘x k k+1 k k-1 2 k k-r+1 r =( C 0 x + C 1 x a + C 2 x a + …. . + Cr xcommon a +…+ Ck x ak) k k k-1 2 k k-r ar+1 + ……. +k. C ak+1) Again multiply +( k. CFirstly, 0 x a + C 1 x a +…. . + Cr x k multiply this with ‘a’ with ‘x’ k+1 k =1. x +( C 1 + k. C 0) xk a +(k. C 2 + k. C 1)xk-1 a 2 We know k. C +that k. C )xak+1 +…. +(k. Cr+k. Cr-1) xk+1 -r ar +…+( k n. C + n. C = n+1 k-1 Cr r r-1 = (k+1)C 0 x(k+1) +(k+1)C 1 x(k+1)-1 a+(k+1)C 2 x(k+1)-2 a 2+…. . +(k+1)Crx(k+1)-rar +…. . . + (k+1)Ck x ak + (k+1)Ck+1 a(k+1)

BINOMIAL THEOREM
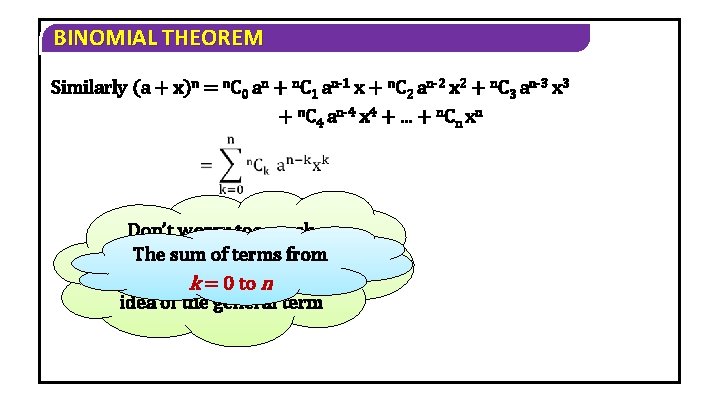
BINOMIAL THEOREM Similarly (a + x)n = n. C 0 an + n. C 1 an-1 x + n. C 2 an-2 x 2 + n. C 3 an-3 x 3 + n. C 4 an-4 x 4 +. . . + n. Cn xn Don’t worry too much about in from The sumwriting of terms notation: kjust = 0 have to n a good idea of the general term

BINOMIAL THEOREM n. C r, A formula for Pascal’s triangle 1 11 121 1331 14641 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 n. C C 0 1 C 1 C 0 1 2 C 2 C 2 C 0 1 2 3 C 3 C 0 1 2 3 4 C 4 C 4 C 0 1 2 3 4 5 C 5 C 5 C 0 1 2 3 4 5 6 C 6 C 0 1 2 3 4 5 6 7 C 7 C 0 1 2 3 4 5 6 7 8 C 8 C 8 C 0 1 2 3 4 5 6 7 8 0 gives the value of row n, term r, if we start numbering the rows and terms from 0 r

BINOMIAL THEOREM Calculate 5 C 3 Formula 5 C 3 Because. . . 5 C 3 But, if we apply n. C formula r

BINOMIAL THEOREM Example (a + 3)5 = 5 C 0 a 5 + 5 C 1 a 4 31 + 5 C 2 a 3 32 + 5 C 3 a 2 33 + 5 C 4 a 1 34 + 5 C 5 35 = a 5 + 5 a 4. 3 + 10 a 3. 9 + 10 a 2. 27 + 5 a. 81 + 243 (a + 3)5= a 5 + 15 a 4 + 90 a 3 + 270 a 2 + 405 a + 243

BINOMIAL THEOREM NOTE Ø The expansion of (x+a)n contains (n+1) terms. Ø In the expansion , the sum of the powers of x and a in each term is equal to n Ø In the expansion, the coefficients binomial coefficients and n. C 0 , n. C 1, n. C 2, ……, n. Cn are called Ø These are simply denoted by C 0 , C 1, C 2…… , Cn

BINOMIAL THEOREM Ø In the expansion , (r+1)th term is called general term. Ø It is denoted by Tr+1 i. e. , Tr+1= n. Cr xn-r ar. (x+a)n = (x-a)n = = n. C 0 xn – n. C 1 xn-1 a+ n. C 2 xn-2 a 2 -. . +(-1)n n. Cnan

BINOMIAL THEOREM Ø (1+x)n = = n. C 0+n. C 1 x+n. C 2 x 2+. . . +n. Cnxn = C 0+C 1 x+C 2 x 2+. . +Cnxn Ø The number of terms in the expansion of (a+b+c)n is (n+2)C 2 Ø The expansion (a+b+c)n is called Trinomial expansion

BINOMIAL THEOREM 1. The number of terms in the expansion of (x+a)n is ___ 1) n 2) (n+1) 3) n+2 C 2 4) (n-1) MCQ S

BINOMIAL THEOREM 2. The general term in the expansion of (x+a)n is _____ 1) Tr+1= n. Cr xn+r ar. 2) Tr+1= n. Cr xn-r a. 3) Tr+1= n. Cr xn-r ar. 4) Tr+1= n. Cr xn-r a-r.

BINOMIAL THEOREM 3. The number of terms in the expansion of (a+b+c)n is _____ 1) n+2 C 2 3) Both 1 & 2 4) None

BINOMIAL THEOREM EXERCISE 6. 1 VERY SHORT ANSWER PROBLEMS

BINOMIAL THEOREM 1) Expand the following using binomial (i) (2 a + 3 b)6 Compare this theorem Solution with ‘(x+a)n’ Given (2 a + 3 b)6 = 6 C 0(2 a)6+ 6 C 1(2 a)5(3 b)+ 6 C 2(2 a)4(3 b)2+6 C 3(2 a)3(3 b)3+ 6 C 4(2 a)2(3 b)4 + 6 C 5(2 a) (3 b)5+ 6 C 6(3 b)6 (x + a)n = n. C xn + n. C xn-1 a + n. C xn-2 a 2 +……+ n. C xn-r ar + …. + n. C an. r n 1 2 3 b 3+4860 a 2 b 4+2916 ab 5+729 b 6 =64 a 6+576 a 5 b+2160 a 4 b 0 2+4320 a

BINOMIAL THEOREM Solution

BINOMIAL THEOREM Solution

BINOMIAL THEOREM = x 8 -4 x 7 -6 x 6+32 x 5+19 x 4 -96 x 3 -54 x 2+108 x+81
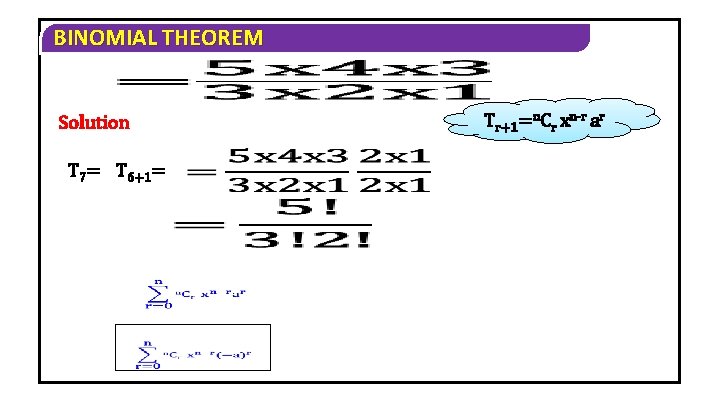
BINOMIAL THEOREM Solution T 7= T 6+1= Tr+1=n. Cr xn-r ar

BINOMIAL THEOREM 3) Find the 4 th term from the end in the expansion of (2 a + 5 b)8. Solution Given (2 a+5 b)8 Tr+1=n. Cr xn-r ar rth term from the end = (n-r+2)th term from the beginning. 4 th term from the last = (8 -4+2)th term from the beginning = 6 th term T 6= T 5+1= 8 C 5(2 a) 8 -5(5 b)5 = 8 C 5(2 a)3(5 b)5 = 8 C 5. 23. a 3. 55. b 5 T 6 = 8 C. 23. 55 a 3 b 5 5

BINOMIAL THEOREM Solution Tr+1 = 10 Cr. 310 -r. x 10 -r-r (-4)r To get the coefficient of x-6, Take 10 -r-r = -6 10+6 = 2 r r=8
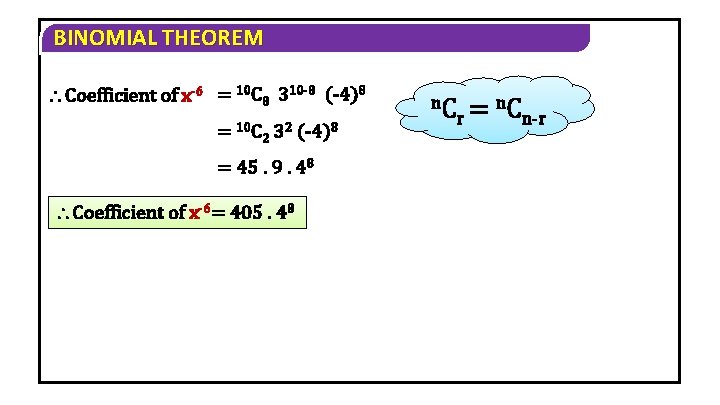
BINOMIAL THEOREM Coefficient of x-6 = 10 C 8 310 -8 (-4)8 = 10 C 2 32 (-4)8 = 45. 9. 48 Coefficient of x-6= 405. 48 n. C = r n-r

BINOMIAL THEOREM Solution Tr+1 = n. Cr xn-r ar

BINOMIAL THEOREM To get the term independent of x, r=10 T 10+1 = 25 C 10(3)25 -10(5)10 T 11 = 25 C 10(3)15(5)10 So 11 th term is the independent term

BINOMIAL THEOREM 6) If the coefficients of (2 r+4)th and (r– 2)nd terms in the expansion of (1+x)18 are equal, find r. Solution Given (1 + x)18 T 2 r + 4 = T(2 r+3)+ 1 =18 C 2 r+3 x 2 r+3 Tr-2 = T(r-3)+ 1 = 18 Cr-3 xr-3 Given condition is coeff. of T 2 r+4 = coeff. of Tr-2
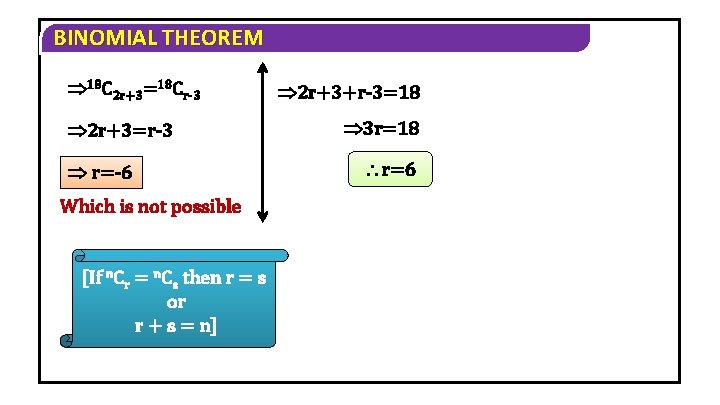
BINOMIAL THEOREM 18 C 2 r+3=18 Cr-3 2 r+3=r-3 r=-6 Which is not possible [If n. Cr = n. Cs then r = s or r + s = n] 2 r+3+r-3=18 3 r=18 r=6

BINOMIAL THEOREM 7) If A and B are the coefficients of xn in the expansion of (1+x)2 n and (1 + x)2 n-1 respectively, then find the value of A/B. Solution Given (1 + x)2 n Tr+1 = 2 n. Cr xr Coeff. of xr = 2 n. Cr A = coeff. of xn A= 2 n. Cn In expansion (1+x)n, Tr+1 = n. Cr xr

BINOMIAL THEOREM Another expansion is (1+x)2 n-1 Tr+1= (2 n-1)Cr. xr Coeff. of xr = (2 n-1)Cr B= coeff. of xn B=(2 n-1)Cn

BINOMIAL THEOREM 2 nc n (2 n-1)c = n

BINOMIAL THEOREM 7 8) Find the number of terms in the expansion. The of (2 x+3 y+z) no. of terms in the Solution expansion of (a+b+c)n is Given expansion is 7 (2 x+3 y+z) No. of terms = n+2 C 2 = 7+2 C 2 = 9 C 2 No. of terms =36 n+2 C [∵ n = 7] 2
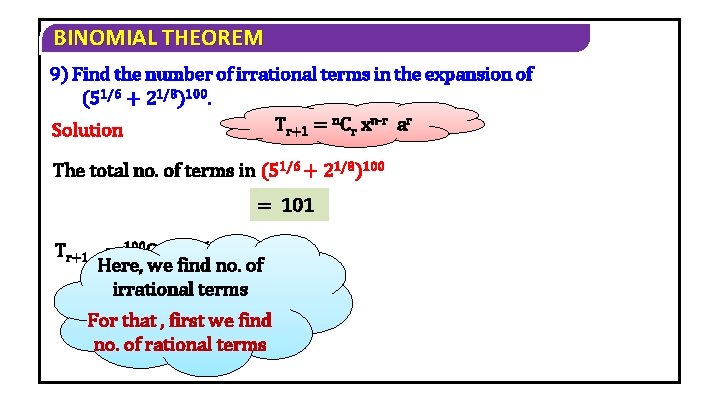
BINOMIAL THEOREM 9) Find the number of irrational terms in the expansion of (51/6 + 21/8)100. Tr+1 = n. Cr xn-r ar Solution The total no. of terms in (51/6 + 21/8)100 = 101 Tr+1 = 100 Cr (51/6)100 -r (21/8)r Here, we find no. of irrational terms For that , first we find no. of rational terms

BINOMIAL THEOREM r = 4, 10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, 82, 88, 94, 100. r = 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96. if r = 16, 40, 64, 88

BINOMIAL THEOREM Number of irrational terms = Total no. of terms – no. of rational terms = 101 – 4 Number of irrational terms = 97.

BINOMIAL THEOREM Thank you…
- Slides: 40