BINOMIAL THEOREM BINOMIAL THEOREM EXERCISE 6 1 LONG

BINOMIAL THEOREM

BINOMIAL THEOREM EXERCISE 6. 1 LONG ANSWER PROBLEMS

BINOMIAL THEOREM Tr+1 = n. Cr xn-r ar Solution

BINOMIAL THEOREM To get the coefficient of x 32, Take 42 – 3 r – 2 r = r=2 32 Coeff. of x 32 = 14 C 2 (2)14 -2 (-3)2 = 14 C 2 (2)12 (3)2 To get the coefficient of x-18, Take 42– 3 r– 2 r= -18 r=12

BINOMIAL THEOREM Coeff. of x -18 = 14 C 12 (2)14 -12 (-3)12 = 14 C 2 (2)2 (3)12 Sum of the coefficients = 14 C 2 (2)12 (3)2 + 14 C 2 (2)2 (3)12 =14 C 2 22 32 (210 + 310) Sum of the coefficients= 14 C 236(210+310).

BINOMIAL THEOREM Solution

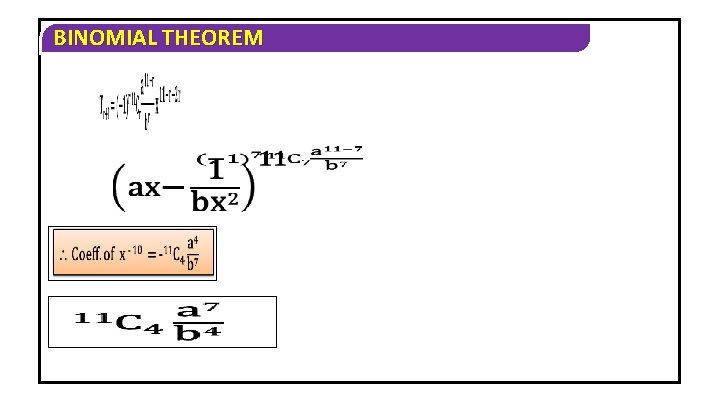
BINOMIAL THEOREM To get the coefficient of x 10, Take 22 – 2 r – r = 10 r = 4

BINOMIAL THEOREM Coeff. of x -10 in To get the coeff. of x -10 , Take 11– r– 2 r = -10 r= 7

BINOMIAL THEOREM Coeff. of x - 10 = n. C By the given condition a 3 b 3 = -1 (ab)3 =(-1)3 ab = -1 n. C = r n-r

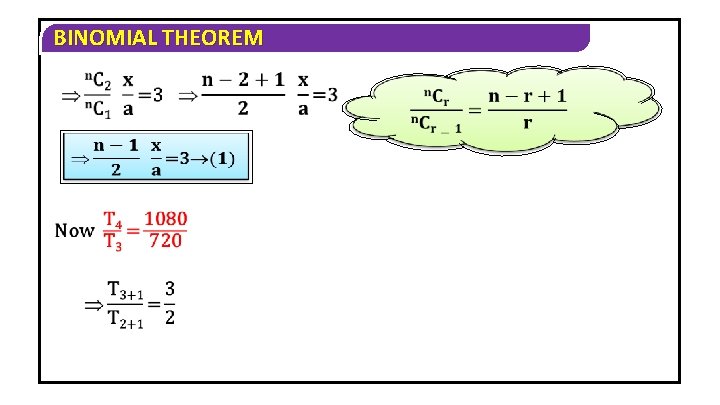
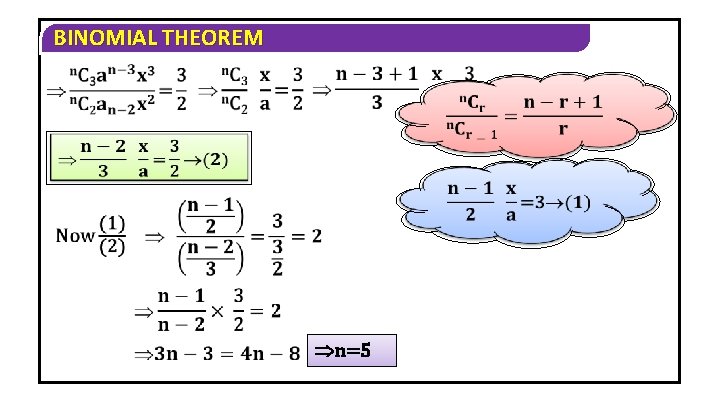
BINOMIAL THEOREM 3) Find the values of a, x and n if the 2 nd, 3 rd and 4 th terms in (a+x)n are 240, 720 and 1080 respectively. Solution Given that in (a + x)n, T 2 = 240, T 3 = 720 and T 4 = 1080 Now Tr+1 = n. Cr an-r xr

BINOMIAL THEOREM

BINOMIAL THEOREM n=5

BINOMIAL THEOREM We know that n=5 Since T 2 = 240

BINOMIAL THEOREM

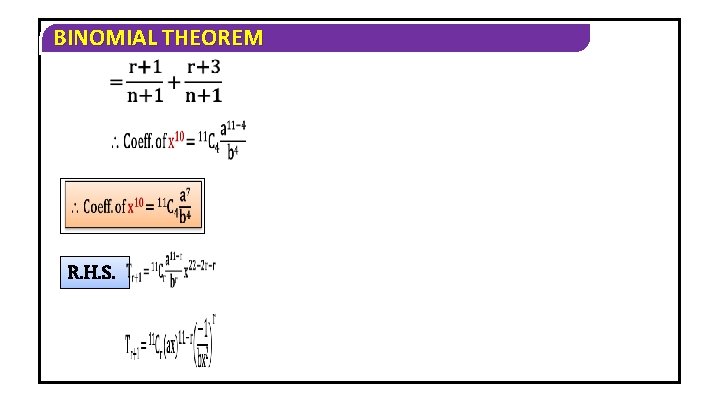
BINOMIAL THEOREM 4) If the coefficients of rth, (r + 1)th and (r + 2)th terms in the expansion of (1 + x)n are in A. P. , then show that n 2 – (4 r + 1)n+4 r 2 – 2= 0 Solution Given expansion is (1 + x)n Tr = T(r-1)+1 = n. Cr-1 x r-1 Tr+1 = n. Cr x r Tr+2 = T(r+1)+1 = n. Cr+1 xr+1

BINOMIAL THEOREM Given condition is n. Cr-1, n. Cr+1 are in A. P 2. n. Cr = n. Cr-1 + n. Cr+1

BINOMIAL THEOREM 2 nr + 2 n – 2 r 2 +2 = 2 r 2 + n 2 – 2 nr + n n 2 + 4 r 2 – 4 nr – n – 2 = 0 n 2 – (4 r + 1) n + 4 r 2 – 2 = 0

BINOMIAL THEOREM Solution Let the coeff. of ‘ 4’ consecutive terms in the expansion of (1 + x)n be a 1=n. Cr , a 2=n. Cr+1 , a 3=n. Cr+2 and a 4=n. Cr+3

BINOMIAL THEOREM L. H. S.

BINOMIAL THEOREM R. H. S.

BINOMIAL THEOREM

BINOMIAL THEOREM 6) If the sum of odd terms and the sum of even terms in the expansion (x + a)n are p and q respectively then show that i) p 2 – q 2 = (x 2 – a 2)n ii) 4 pq = (x + a)2 n – (x – a)2 n Solution Given that p = sum of odd terms in the expansion of (x + a)n q = sum of even terms in the expansion of (x + a)n

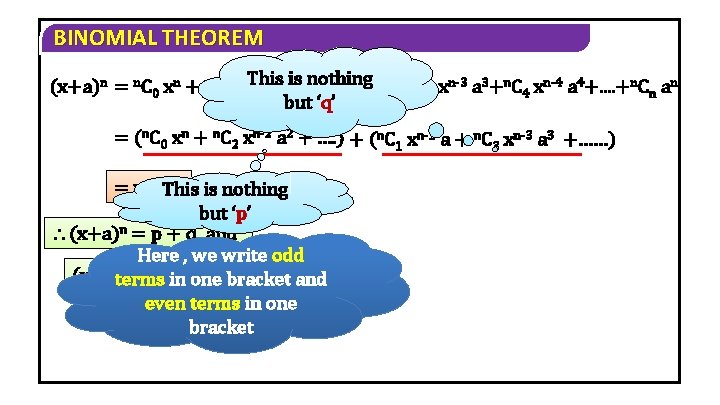
BINOMIAL THEOREM This n. C xn-2 a 2 +n. C xn-3 a 3+n. C xn-4 a 4+. . +n. C an (x+a)n = n. C 0 xn + n. C 1 xn-1 a 1 is + nothing 2 3 4 n but ‘q’ = (n. C 0 xn + n. C 2 xn-2 a 2 + …. ) + (n. C 1 xn-1 a + n. C 3 xn-3 a 3 +……) = p +This q is nothing but ‘p’ (x+a)n = p + q and Here , we write odd n (x - a)terms = p in - qone bracket and even terms in one bracket

BINOMIAL THEOREM i) L. H. S p 2 – q 2 = (p + q)(p – q) = (x + a)n (x – a)n (a + b)2 – (a – b)2 = 4 ab = [(x + a) (x – a)]n = [x 2 – a 2]n ii) L. H. S 4 pq = (p + q)2 – (p – q)2 =[(x + a)n]2 – [(x – a)n]2 = (x + a)2 n - (x – a)2 n = R. H. S.

BINOMIAL THEOREM 7) By using binomial theorem for all positive integers n, show that 2 i) 50 n – 49 n – 1 is divisible by 492 Take ‘(49) ‘ as common n Solution Given expansion is (50) = (1 + 49)n = n. C 0 + n. C 1. 49 + n. C 2. (49)2 + n. C 3 (49)3 + …. + n. Cn (49)n 50 n = 1 + n. 49 + (49)2 [n. C 2 + n. C 3. 49 + …. + n. Cn (49)n-2] (50)n – 49 n – 1 = (49)2 some integer. (50)n – 49 n – 1 is divisible by (49)2

BINOMIAL THEOREM ii) 62 n – 35 n – 1 is divisible by 1225. 2 ‘ as Take ‘(35) Solution Given 62 n – 35 n – 1 is divisible by 1225. common Now 62 n = (62)n = 36 n = (1+35)n = n. C 0 + n. C 1 35 + n. C 2 (35)2 + n. C 3 (35)3 + …. + n. Cn (35)n 62 n = 1 + n. 35 + (35)2 [n. C 2 + n. C 3. 35 + …. + n. Cn (35)n-2] 62 n – 35 n – 1 = (35)2 some integer = 1225 some integer 62 n – 35 n – 1 is divisible by 1225.

BINOMIAL THEOREM Solution

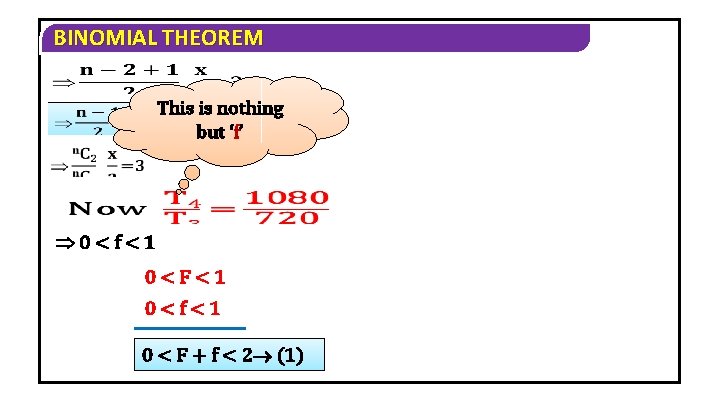
BINOMIAL THEOREM This is nothing but ‘f’ 0<f<1 0<F<1 0<f<1 0 < F + f < 2 (1)

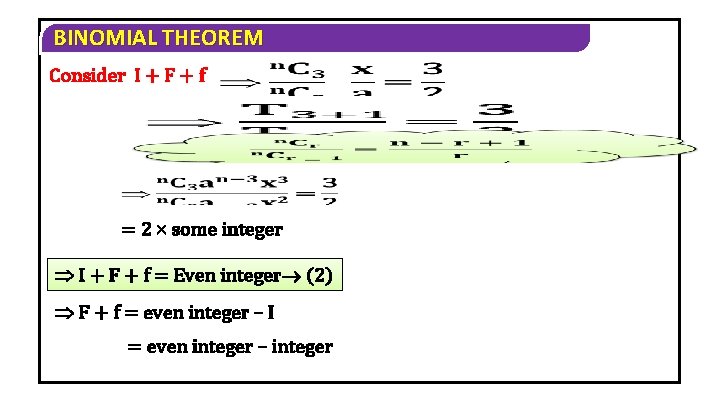
BINOMIAL THEOREM Consider I + F + f = 2 some integer I + F + f = Even integer (2) F + f = even integer – I = even integer – integer

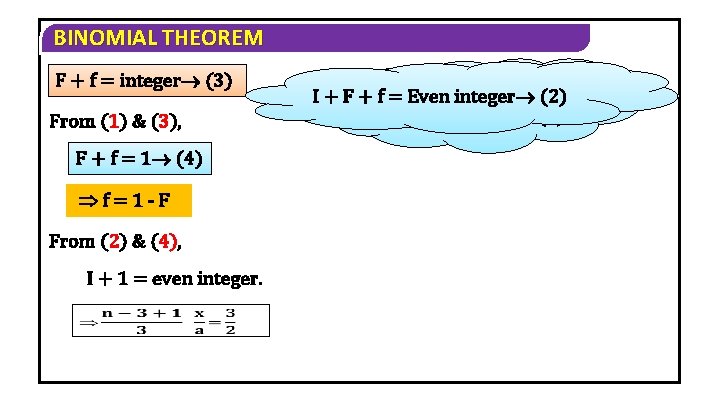
BINOMIAL THEOREM F + f = integer (3) From (1) & (3), F + f = 1 (4) f=1 -F From (2) & (4), I + 1 = even integer. F + integer f < 2 (1) I + F + f 0=<Even (2) F + f = integer (3)

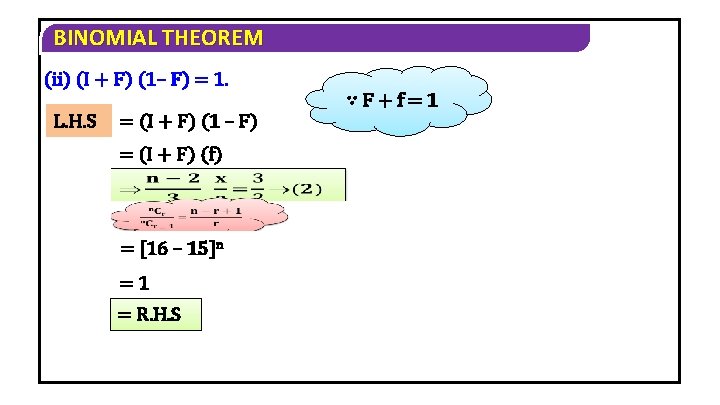
BINOMIAL THEOREM (ii) (I + F) (1– F) = 1. ∵F+f=1 L. H. S = (I + F) (1 – F) = (I + F) (f) = [16 – 15]n =1 = R. H. S

BINOMIAL THEOREM Thank you…