Binomial regression Greg Francis PSY 626 Bayesian Statistics

Binomial regression Greg Francis PSY 626: Bayesian Statistics for Psychological Science Fall 2020 Purdue University

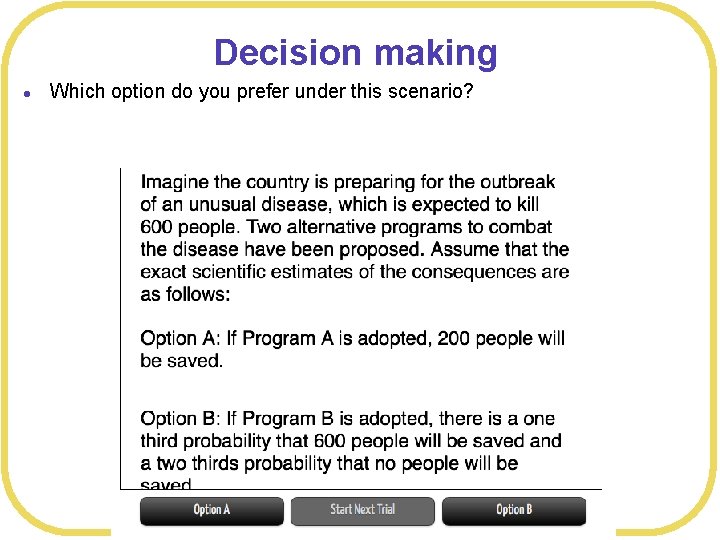
Decision making l Which option do you prefer under this scenario?

Decision making l Framing effects

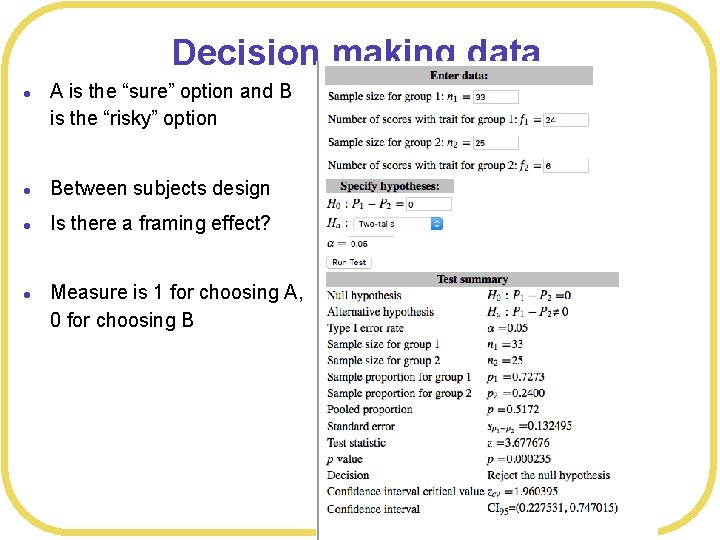
Decision making data l A is the “sure” option and B is the “risky” option l Between subjects design l Is there a framing effect? l Measure is 1 for choosing A, 0 for choosing B

Binomial model l yi is number of observed outcomes (e. g. , correct responses) from n draws when the probability of a correct response is pi l We know n for any trial is 1 l We estimate pi l It is convenient to actually estimate the logit of pi

Binomial regression l We will model the logit as a linear equation l Among other things, this insures that our pi value is always between 0 and 1 (as all probabilities must be) w Makes it easier to identify priors l Our MAP estimate will gives us logit(pi), to get back pi we have to invert

Model l l l # Different probabilities DMdata$Condition. Index <- coerce_index(DMdata$Statement. Type) # 2 is Save, 1 is Die DMmodel 1 <- map( Quadratic approximate posterior distribution alist( Choose. A ~ dbinom(1, p), Formula: logit(p) <- a[Condition. Index], Choose. A ~ dbinom(1, p) logit(p) <- a[Condition. Index] ~ dnorm(0, 10) ), data= DMdata ) Posterior means: a[1] a[2] -1. 1501588 0. 9793339 Log-likelihood: -33. 11 >

Posterior l post<-extract. samples(DMmodel 1, n= 1000) l dens(logistic(post$a[, 1])) l > HPDI(logistic(post$a[, 1])) l |0. 89| l 0. 1191296 0. 3841165 l > HPDI(logistic(post$a[, 2])) l |0. 89| l 0. 6212017 0. 8412435

Posterior l > Save. Post <- logistic(post$a[, 2]) l > Die. Post <- logistic(post$a[, 1]) l > l l l > cat("Probability p_Save > p_Die = ", length(Save. Post[Save. Post> Die. Post])/length(Save. Post) ) Probability p_Save > p_Die = 1 No need for a null model for comparison, can just look at the posteriors

Model comparison l # Null model l DMmodel 0 <- map( l alist( Choose. A ~ dbinom(1, p), l logit(p) <- a, l a ~ dnorm(0, 10) l ), data= DMdata ) Choose. A ~ dbinom(1, p) Quadratic approximate posterior distribution Formula: l l print(precis(DMmodel 0)) logit(p) <- a a ~ dnorm(0, 10) Posterior means: a > cat("Probability of Sure response: ", logistic(a)) 0. 06898238 Probability of Sure response: 0. 5172388 Log-likelihood: -40. 17 >

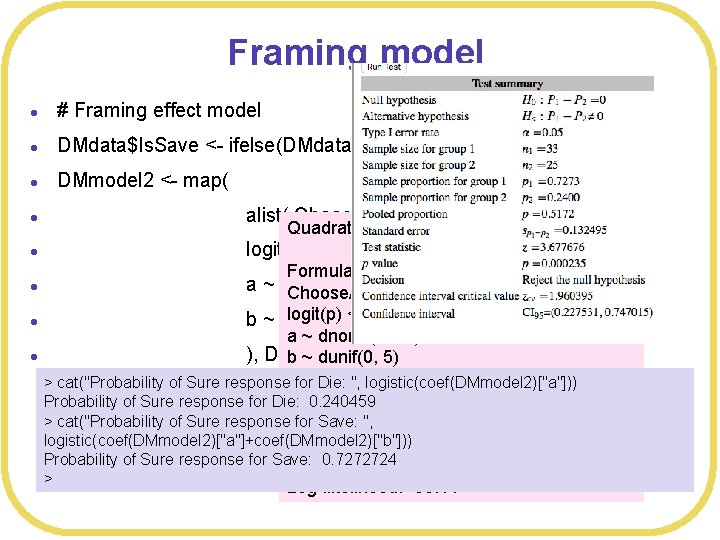
Framing model l # Framing effect model l DMdata$Is. Save <- ifelse(DMdata$Statement. Type=="Save", 1, 0) l DMmodel 2 <- map( l alist( Choose. A ~ dbinom(1, p), l logit(p) <- a + b*Is. Save, l a ~ dnorm(0, 10), Choose. A ~ dbinom(1, p) l logit(p) <- a + b * Is. Save b ~ dunif(0, 5) Quadratic approximate posterior distribution Formula: l a ~ dnorm(0, 10) ), DMdata ) b ~ dunif(0, 5) > cat("Probability of Sure response for Die: ", logistic(coef(DMmodel 2)["a"])) Posterior means: Probability of Sure response for Die: 0. 240459 > cat("Probability of Sure response for Save: ", a b logistic(coef(DMmodel 2)["a"]+coef(DMmodel 2)["b"])) -1. 150165 2. 130992 Probability of Sure response for Save: 0. 7272724 > Log-likelihood: -33. 11

Model comparison > compare(DMmodel 0, DMmodel 1, DMmodel 2) WAIC SE d. WAIC d. SE p. WAIC weight DMmodel 2 70. 3 7. 27 0. 0 NA 2. 0 0. 51 DMmodel 1 70. 4 7. 28 0. 1 0. 07 2. 1 0. 49 DMmodel 0 82. 3 0. 54 12. 1 7. 31 1. 0 0. 00 > l l Not much difference between different proportions and Framing effect model Only difference is the priors, really

Zenner Cards l Guess which card appears next:

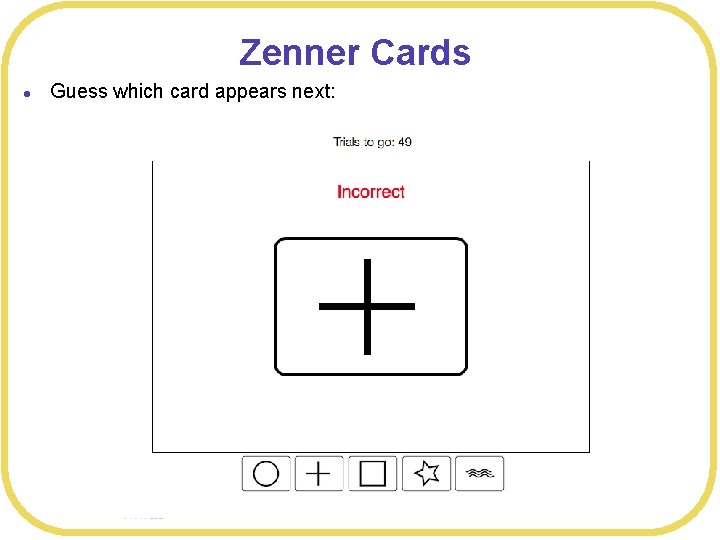
Zenner Cards l Guess which card appears next:

Zenner Cards l Guess which card appears next:

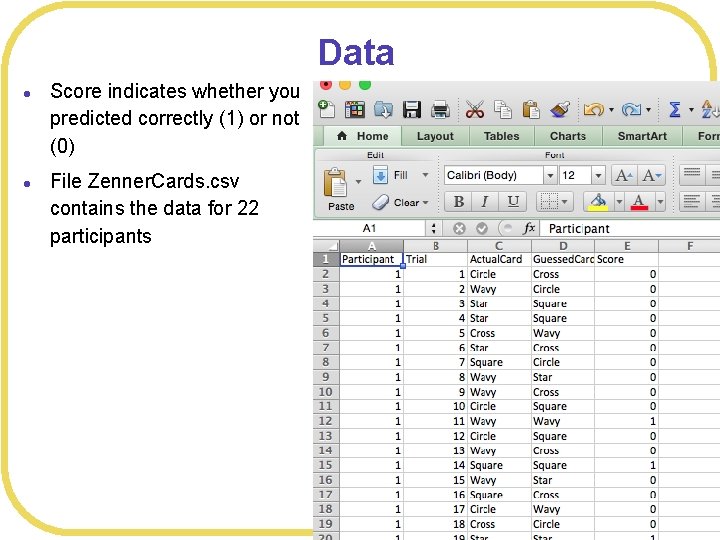
Data l l Score indicates whether you predicted correctly (1) or not (0) File Zenner. Cards. csv contains the data for 22 participants

Loading data l # load full data file l ZCdata<read. csv(file="Zenner. Cards. csv", header=TRUE, strings. As. Factors=FALSE) l # load the rethinking library l library(rethinking) l # Dummy variables to indicate actual card type and guessed card type l ZCdata$Card. Index <- coerce_index(ZCdata$Actual. Card) l ZCdata$Selected. Card. Index <- coerce_index(ZCdata$Guessed. Card)

Model set up l # All cards and subjects treated the same l ZCmodel 1 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a, l a ~ dnorm(0, 10) l ), data= ZCdata )

Model results l Maximum a posteriori (MAP) model fit l Formula: l Score ~ dbinom(1, p) l logit(p) <- a l a ~ dnorm(0, 10) l MAP values: l a l -1. 313936 l Log-likelihood: -567. 99 l a is logit(p) w a=coef(ZCmodel 1)["a”] l cat("Probability of correct response: ", logistic(a)) l Probability of correct response: 0. 211829

Model results l > precis(ZCmodel 1) l Mean Std. Dev 5. 5% 94. 5% l a -1. 31 0. 07 -1. 43 -1. 2 > logistic(-1. 43) [1] 0. 1930987 > logistic(-1. 2) [1] 0. 2314752

Differences across cards l # Different probabilities for different actual cards l ZCmodel 2 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a[Card. Index], l a[Card. Index] ~ dnorm(0, 10) l l l > print(precis(ZCmodel 2, depth=2)) ), data= ZCdata ) mean sd 5. 5% 94. 5% print(precis(ZCmodel 2, depth=2)) a[1] -1. 503674 0. 1747523 -1. 782962 -1. 2243857 a[2] -1. 122725 0. 1566305 -1. 373050 -0. 8723989 cat("Probability of correct response: ", logistic(coef(ZCmodel 2))) a[3] -1. 003646 0. 1521598 -1. 246827 -0. 7604656 a[4] -1. 503622 0. 1747495 -1. 782906 -1. 2243390 a[5] -1. 503585 0. 1747474 -1. 782865 -1. 2243046 > > cat("Probability of correct response: ", logistic(coef(ZCmodel 2))) Probability of correct response: 0. 1818782 0. 2455062 0. 2682251 0. 1818859 0. 1818915 >

Differences across cards l compare(ZCmodel 1, ZCmodel 2) l l ZCmodel 2 1137. 3 36. 08 0. 0 NA 5. 2 0. 58 l ZCmodel 1 1138. 0 35. 58 0. 7 6. 15 1. 0 0. 42 l A model that uses different probabilities for different cards is expected to WAIC SE d. WAIC d. SE p. WAIC weight do better than a model that ignores card type. w But not much better l Does this suggest that people have some kind of predictive power?

Differences in guesses l It might be better to see if participant’s guesses improve model fit l # Different probabilities for different selected cards l ZCmodel 3 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a[Selected. Card. Index], l a[Selected. Card. Index] ~ dnorm(0, 10) l ), data= ZCdata ) l Quadratic approximate posterior distribution l Formula: l Score ~ dbinom(1, p) l logit(p) <- a[Selected. Card. Index] l a[Selected. Card. Index] ~ dnorm(0, 10) l Posterior means: l a[1] a[2] a[3] a[4] a[5] l -1. 440574 -1. 318974 -1. 169227 -1. 509157 -1. 139058 l Log-likelihood: -566. 16 > cat("Probability of correct response: ", logistic(coef(ZCmodel 3))) Probability of correct response: 0. 1914565 0. 210989 0. 2369947 0. 1810637 0. 2424933

Null model l Put a tight prior on a to be around logit(0. 2) l # Null model (p=0. 2) l ZCmodel 0 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a, l a ~ dnorm(logit(0. 2), 0. 001) l ), data= ZCdata ) l Quadratic approximate posterior distribution l Formula: l Score ~ dbinom(1, p) l logit(p) <- a l a ~ dnorm(logit(0. 2), 0. 001) l Posterior means: l a l -1. 386281 l Log-likelihood: -568. 46 p=0. 2000021

Comparing models l All models l > compare(ZCmodel 0, ZCmodel 1, ZCmodel 2, ZCmodel 3, n=10000) l l ZCmodel 0 1136. 9 37. 57 0. 0 NA 0. 0 0. 38 l ZCmodel 2 1137. 0 35. 98 0. 1 6. 47 5. 0 0. 37 l ZCmodel 1 1138. 0 35. 65 1. 1 1. 92 1. 0 0. 22 l ZCmodel 3 1142. 5 35. 88 5. 5 4. 27 5. 1 0. 02 l > l WAIC SE d. WAIC d. SE p. WAIC weight Null model slightly beats model with different probabilities for different cards l Cannot rule out model that does better for some cards than other cards l Can rule out model that has differences for different responses

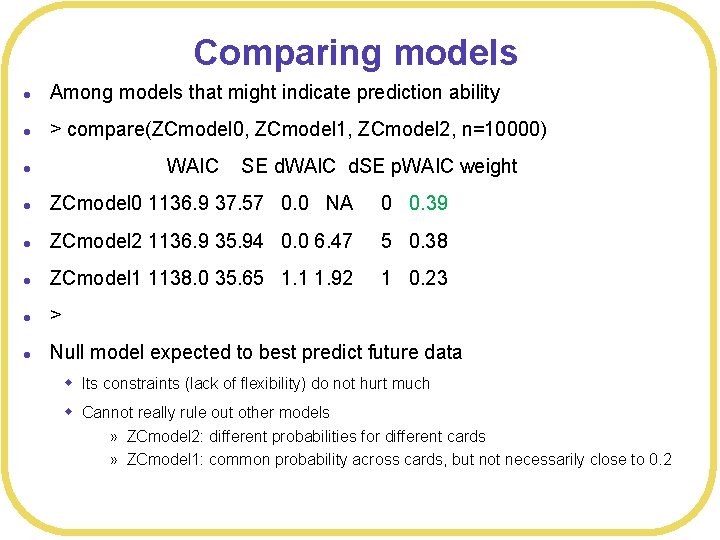
Comparing models l Among models that might indicate prediction ability l > compare(ZCmodel 0, ZCmodel 1, ZCmodel 2, n=10000) l l ZCmodel 0 1136. 9 37. 57 0. 0 NA 0 0. 39 l ZCmodel 2 1136. 9 35. 94 0. 0 6. 47 5 0. 38 l ZCmodel 1 1138. 0 35. 65 1. 1 1. 92 1 0. 23 l > l Null model expected to best predict future data WAIC SE d. WAIC d. SE p. WAIC weight w Its constraints (lack of flexibility) do not hurt much w Cannot really rule out other models » ZCmodel 2: different probabilities for different cards » ZCmodel 1: common probability across cards, but not necessarily close to 0. 2

Probability of correct response: 0. 1203796 Different probabilities for each participant 0. 3201281 0. 2002569 0. 160332 ZCmodel 4 <- map( 0. 1802764 0. 1803053 alist( Score ~ dbinom(1, p), 0. 2202524 0. 2203118 logit(p) <- a[Participant], 0. 320144 0. 2002538 a[Participant] ~ dnorm(0, 10) 0. 2402412 0. 1403437 ), data= ZCdata ) 0. 1803359 0. 2202592 Quadratic approximate posterior distribution 0. 1802745 Formula: 0. 3401226 Score ~ dbinom(1, p) 0. 2601786 logit(p) <- a[Participant] 0. 1802779 0. 2402599 a[Participant] ~ dnorm(0, 10) 0. 2402402 Posterior means: 0. 1203833 a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9] a[10] a[11] a[12] a[13] 0. 2002959 Participants? l l l l -1. 9888408 -0. 7531832 -1. 3846893 -1. 6557598 -1. 5144763 -1. 5142806 -1. 2641961 -1. 2638502 -0. 7531100 -1. 3847090 -1. 1513577 1. 8124385 -1. 5140731 l a[14] a[15] a[16] a[17] a[18] a[19] a[20] a[21] a[22] l -1. 2641565 -1. 5144887 -0. 6627480 -1. 0450403 -1. 5144660 -1. 1512553 -1. 1513631 -1. 9888057 -1. 3844459 l Log-likelihood: -556. 92

Comparing models l > compare(ZCmodel 0, ZCmodel 2, ZCmodel 3, ZCmodel 4, n=10000) l l ZCmodel 0 1136. 9 37. 57 0. 0 NA 0. 0 0. 49 l ZCmodel 2 1137. 0 35. 93 0. 1 6. 49 5. 0 0. 48 l ZCmodel 3 1142. 4 35. 86 5. 4 4. 26 5. 0 0. 03 l ZCmodel 4 1158. 4 36. 88 21. 4 9. 93 22. 1 0. 00 l > l WAIC SE d. WAIC d. SE p. WAIC weight Little support for ZCmodel 4 with individual differences (at least relative to the other models)

Participants and cards? l ZCmodel 5 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a[Card. Index] + b[Participant], l a[Card. Index] ~ dnorm(0, 10), l b[Participant] ~ dnorm(0, 10) l ), data= ZCdata ) l Quadratic approximate posterior distribution l Formula: l Score ~ dbinom(1, p) l logit(p) <- a[Card. Index] + b[Participant] l a[Card. Index] ~ dnorm(0, 10) l b[Participant] ~ dnorm(0, 10) l Posterior means: l a[1] a[2] a[3] a[4] a[5] b[1] b[2] b[3] b[4] b[5] b[6] l -1. 29046411 -0. 90151302 -0. 77955561 -1. 29045875 -1. 29046761 -0. 89955658 0. 34761619 -0. 29047384 -0. 56403964 -0. 42147400 -0. 42137773 l b[7] b[8] b[9] b[10] b[11] b[12] b[13] b[14] b[15] b[16] b[17] l -0. 16901236 -0. 16898745 0. 34764304 -0. 29043124 -0. 05504806 -0. 72178762 -0. 42131146 -0. 16895572 -0. 42141992 0. 43908191 0. 05257936 l b[18] b[19] b[20] b[21] b[22] l -0. 42135670 -0. 05505267 -0. 05506810 -0. 89954578 -0. 29050647 l Log-likelihood: -552. 29 l >

Looking at probabilities l a. Values 5<-c() l for(p in unique(ZCdata$Participant)){ l for(p 2 in unique(ZCdata$Card. Index)){ l code<-sprintf("b[%d]", p) l code 2<-sprintf("a[%d]", p 2) l a. Values 5<- c(a. Values 5, coef(ZCmodel 5)[code] + coef(ZCmodel 5)[code 2]) l } l > cat("Probability of correct response: ", logistic(a. Values 5)) l Probability of correct response: 0. 1006502 0. 1417209 0. 1572131 0. 1006507 0. 1006499 0. 2803254 0. 3649608 0. 3936633 0. 2803265 0. 2803247 0. 1706627 0. 2329038 0. 2553975 0. 1706634 0. 1706622 0. 135345 0. 1876195 0. 2069194 0. 1353456 0. 1353446 0. 1529125 0. 2103218 0. 2312921 0. 1529132 0. 1529121 0. 152925 0. 2103377 0. 2313092 0. 1529257 0. 1529245 0. 1885474 0. 2553032 0. 2791729 0. 1885482 0. 1885469 0. 1885512 0. 2553079 0. 2791779 0. 188552 0. 1885507 0. 2803309 0. 364967 0. 3936697 0. 2803319 0. 2803301 0. 1706687 0. 2329114 0. 2554056 0. 1706695 0. 1706682 0. 206605 0. 2775673 0. 3026725 0. 2066059 0. 2066045 0. 1179226 0. 1647502 0. 1822253 0. 1179231 0. 1179222 0. 1529336 0. 2103488 0. 231321 0. 1529343 0. 1529331 0. 1885561 0. 255314 0. 2791843 0. 1885569 0. 1885555 0. 1529195 0. 2103307 0. 2313017 0. 1529202 0. 1529191 0. 299143 0. 3864093 0. 4156944 0. 2991441 0. 2991423 0. 2248044 0. 2996566 0. 3258586 0. 2248053 0. 2248038 0. 1529277 0. 2103412 0. 231313 0. 1529284 0. 1529272 0. 2066043 0. 2775663 0. 3026716 0. 2066052 0. 2066037 0. 2066018 0. 2775632 0. 3026683 0. 2066026 0. 2066012 0. 1006512 0. 1417222 0. 1572145 0. 1006517 0. 1006509 0. 1706581 0. 2328979 0. 2553913 0. 1706588 0. 1706576

Comparing models l > compare(ZCmodel 0, ZCmodel 1, ZCmodel 4, ZCmodel 2, ZCmodel 5, n=10000) l l ZCmodel 2 1136. 9 35. 99 0. 0 NA 5. 0 0. 39 l ZCmodel 0 1136. 9 37. 57 0. 0 6. 46 0. 0 0. 39 l ZCmodel 1 1138. 0 35. 68 1. 1 6. 12 1. 0 0. 22 l ZCmodel 5 1157. 3 37. 26 20. 4 9. 89 26. 2 0. 00 l ZCmodel 4 1158. 4 36. 86 21. 5 11. 48 22. 2 0. 00 l WAIC SE d. WAIC d. SE p. WAIC weight Virtually no support for a model with different probabilities for cards and participants

Interaction model? l l l What about a model that takes into account the card and the selected card? We make a new index: ZCdata$Interaction. Index <- 1+ 5*(ZCdata$Selected. Card. Index-1) + (ZCdata$Card. Index-1) l > unique(ZCdata$Interaction. Index) l [1] 6 5 14 22 9 3 20 10 11 25 13 8 21 2 19 12 4 17 23 1 15 7 18 24 16 l ZCmodel 6 <- map( l alist( Score ~ dbinom(1, p), l logit(p) <- a[Interaction. Index], l a[Interaction. Index] ~ dnorm(0, 10) l ), data= ZCdata )

Comparing models l > compare(ZCmodel 0, ZCmodel 1, ZCmodel 3, ZCmodel 4, ZCmodel 5, ZCmodel 6) l WAIC SE d. WAIC d. SE p. WAIC weight l ZCmodel 6 479. 2 3. 49 0. 0 NA 178. 1 1 l ZCmodel 0 1136. 9 37. 57 657. 7 38. 21 0. 0 0 l ZCmodel 1 1138. 1 35. 55 658. 9 36. 19 1. 1 0 l ZCmodel 3 1142. 1 35. 89 662. 9 36. 51 4. 9 0 l ZCmodel 5 1157. 1 37. 15 677. 8 37. 62 26. 0 0 l ZCmodel 4 1157. 8 36. 85 678. 5 37. 47 21. 8 0 l Looks like we have a winner!

Interaction model l Subjects are more successful for some combination of cards and guesses? w Duh! w Type Circle, guess Circle will be 100% correct w Type Circle, guess anything else will be 0% correct l This ”model” just describes the definition of whether a guess is correct or not w It’s not a viable model in any meaningful sense

Trial effects l l Modify the code to look for a trial effect Does a model that includes just trial effects (no card or participant effects) beat the null model?